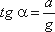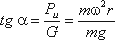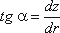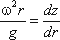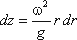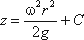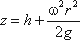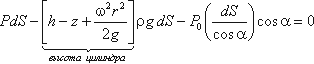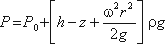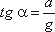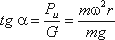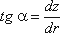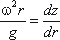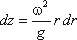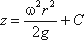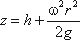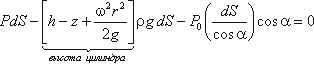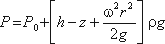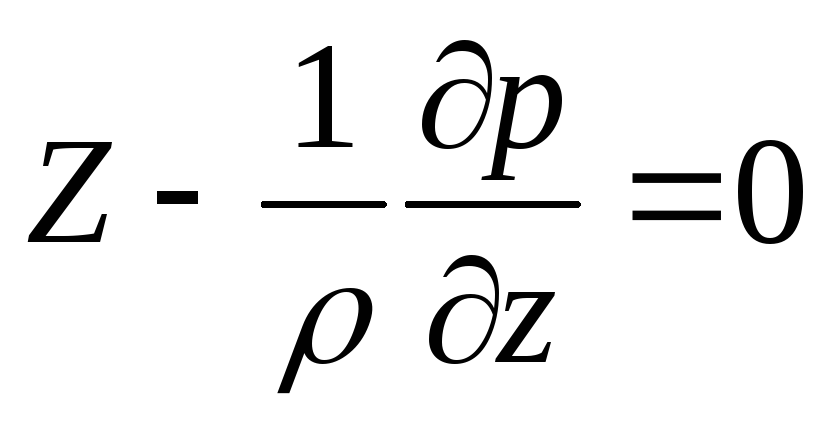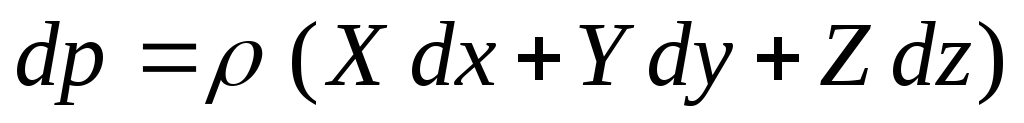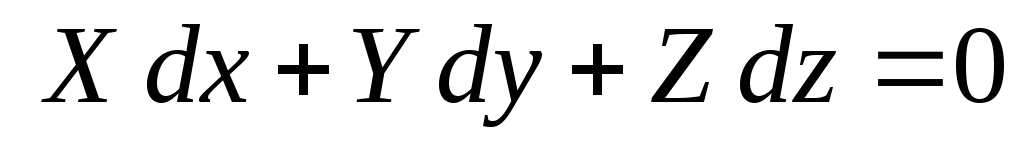какую форму имеет поверхность равного давления при абсолютном покое жидкости
Поверхности равного давления. Формы свободной поверхности жидкости
Поверхностями равного давления называются поверхности с одинаковыми во всех точках давлениями. Тогда любая горизонтальная плоскость, проведенная в покоящейся жидкости, находящейся под действием силы тяжести, является поверхностью равного давления.
Свободной поверхностью называют плоскость раздела между жидкостью и газообразной средой. Равнодействующая всех сил, приложенных к каждой частице, лежащей на свободной поверхности покоящейся жидкости, нормальна к этой поверхности.
Рассмотрим формы свободной поверхности жидкости для следующих случаев:
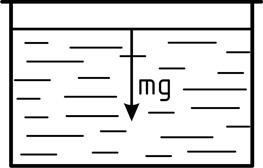
1 – жидкость находится в покое под действием силы тяжести (рис. 2.4).
В этом случае на каждую частицу жидкости действует только одна сила – сила тяжести mg, которая направлена вертикально вниз, а свободная поверхность есть горизонтальная плоскость.
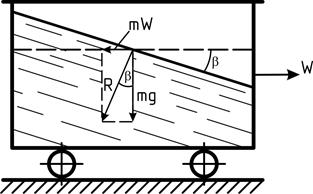
2 – жидкость находится в относительном покое по отношению к сосуду, движущемуся по горизонтальному пути с постоянным ускорением W (рис. 2.5).
В этом случае на каждую частицу жидкости действует сила тяжести mg и сила инерции mW, которая направлена в сторону, обратную ускорению. Равнодействующая этих сил составит с вертикалью угол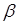 
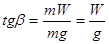
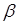
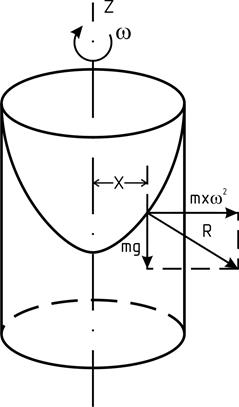
, тогда 
, а т.к. свободная поверхность должна быть нормальна к равнодействующей, то она будет представлять собой наклонную плоскость, составляющую с горизонтом тот же угол .
3 – относительное равновесие жидкости во вращающихся сосудах (рис. 2.6), ими могут быть центрифуги, сепараторы.
В этом случае на любую частицу жидкости при ее относительном равновесии будут действовать сила тяжести mg и нормальная сила инерции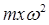 
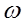
, где 
– расстояние частицы от оси вращения; 
– угловая скорость равномерного вращения сосуда. Свободная поверхность жидкости будет в каждой точке нормальна к равнодействующей R этих сил и будет представлять собой параболоид вращения вокруг оси z.
Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называетсяповерхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
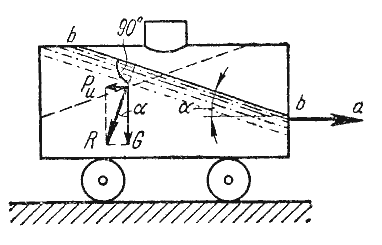
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рисунок2.6).
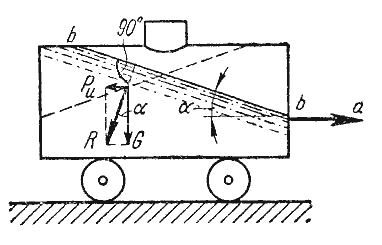
Рисунок 2.6 Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерцииPu, равная по величине ma. Равнодействующая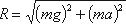 
этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рисунок2.6, пунктир).
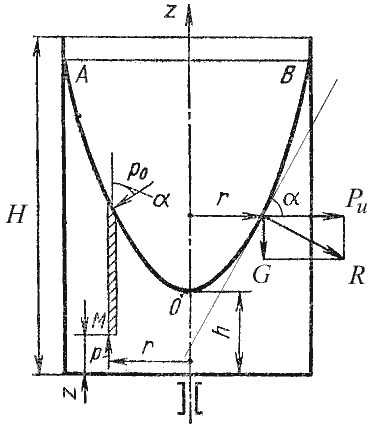
Рисунок 2.7 Вращение сосуда с жидкостью
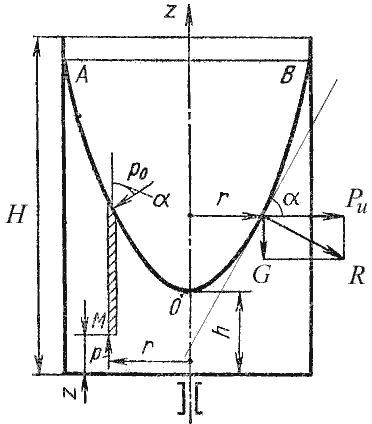
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
Дата добавления: 2016-02-20 ; просмотров: 499 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.
Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая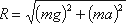 
этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
После сокращений получим
Это значит, что давление возрастает пропорционально радиусу r и уменьшается пропорционально высоте z.
5. Поверхности равного давления
Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем. Рассмотрим два примера такого относительного покоя.
В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).
Рис. 2.6. Движение цистерны с ускорением
К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции Pu, равная по величине ma. Равнодействующая 
этих сил направлена к вертикали под углом α, тангенс которого равен
Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).
Рис. 2.7. Вращение сосуда с жидкостью
Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим
или после интегрирования
В точке пересечения кривой АОВ с осью вращения r = 0, z = h = C, поэтому окончательно будем иметь
т.е. кривая АОВ является параболой, а свободная поверхность жидкости параболоидом. Такую же форму имеют и другие поверхности уровня.
Для определения закона изменения давления во вращающейся жидкости в функции радиуса и высоты выделим вертикальный цилиндрический объем жидкости с основанием в виде элементарной горизонтальной площадки dS (точка М) на произвольном радиусе r и высоте z и запишем условие его равновесия в вертикальном направлении. С учетом уравнения (2.11) будем иметь
5. Гидростатическое давление и его свойства. Дифференциальные уравнения равновесия жидкости. Поверхности равного давления
В общем случае поверхностная сила 
, действующая на площадке
, направлена под некоторым углом к ней. Ее можно разложить на нормальную
и тангенциальную
составляющие.
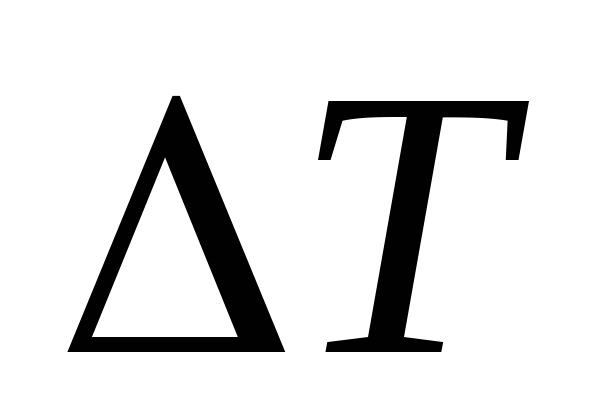
Сила 
, если она направлена внутрь объема, называетсясилой давления.
Сила 
называетсясилой трения.
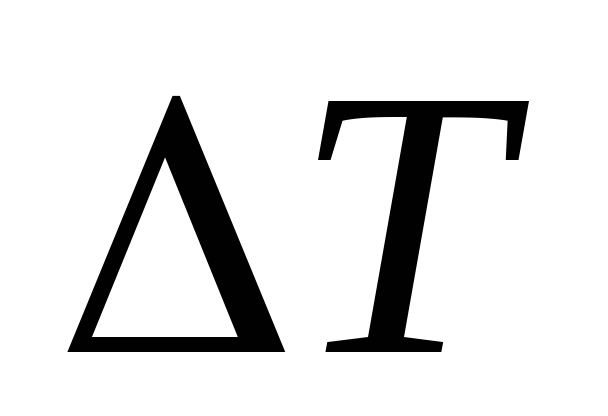
Как массовые, так и поверхностные силы в гидромеханике рассматривают обычно в виде единичных сил, т. е. сил, отнесенных к соответствующим единицам.
Массовые силы относят к единице массы, а поверхностные – к единице площади.
Так как всякая массовая сила равна произведению массы на ускорение, то, следовательно, единичная массовая сила численно равна соответствующему ускорению.
Единичная поверхностная сила, называемая напряжением поверхностной силы, как и всякая сила, раскладывается на нормальное и касательное напряжения.
Нормальное напряжение, т. е. напряжение силы давления, называется гидромеханическим (в случае покоя – гидростатическим)) давлением или просто давлением и обозначается буквой р.
В общем случае гидромеханическое давление в данной точке равно пределу, к которому стремится отношение силы давления к площадке, на которую она действует, при стремлении величины площадки к нулю, т. е. при стягивании площадки в точку:
.
Если сила давления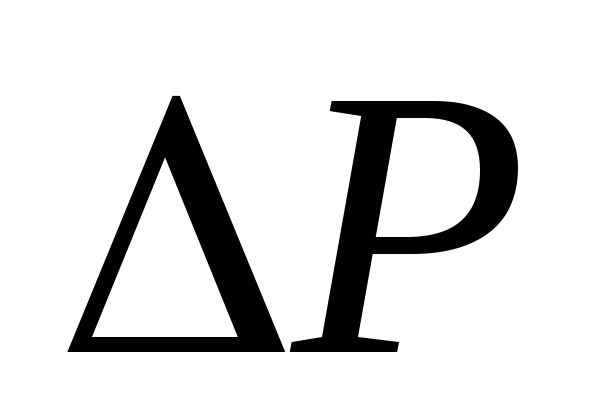 
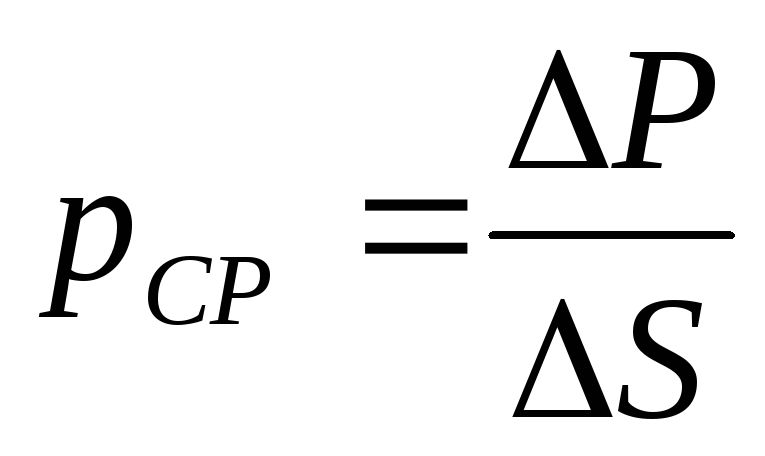
равномерно распределена по площадке
или ищут среднее значение гидромеханического давления, то последнее определяют по формуле:
.
Если давление р отсчитывается от нуля, то оно называется абсолютным.
Если давление р отсчитывается от атмосферного, то оно называется избыточным, или манометрическим.
За единицу давления в международной системе единиц (СИ) принято равномерно распределенное давление, при котором на площадь 1 м 2 действует сила 1 ньютон, т. е. 1 Н/м 2 [Паскаль].
Внесистемная единица – техническая атмосфера равна килограмму-силе на см 2 [1 кгс/см 2 ].
Касательное напряжение в жидкости, т. е. напряжение трения, обозначается буквой 
и выражается подобно давлению пределом:
Гидростатическое давление отличается тремя свойствами:
1. Гидростатическое давление направлено по внутренней нормали к площадке, на которую оно действует. Если поверхность криволинейная, то давление направлено нормально к касательной этой поверхности.
2. Гидростатическое давление в точке жидкости одинаково по всем направлениям или, иначе, гидростатическое давление не зависит от ориентации площадки, на которую оно действует;
3. Гидростатическое давление зависит от координат (от положения) рассматриваемой точки внутри жидкости и от внешнего давления, приложенного к свободной поверхности жидкости.
Дифференциальные уравнения равновесия жидкости:
Основное дифференциальное уравнение гидростатики:
Сумма в скобках правой части уравнения выражает энергию, отнесенную к массе.
Выражение в скобках в правой части уравнения при ρ = const есть полный дифференциал некоторой функцииU (х, у, z).
Функцию U (х, у, z) называютпотенциалом массовых сил, илисиловой функцией. Силы, для которых существует эта функция, называют силами, имеющими потенциал.
Основн о е уравнение гидростатики (1-я форма):
Основн о е уравнение гидростатики (2-я форма):
Произведение γh называютвесовым давлением.
Различают три вида гидростатического давления в точке жидкости:
Под абсолютным давлением(рА )в точке жидкости понимают давление с учетом атмосферного давления.
Под избыточным давлением(р)в точке понимают превышение абсолютного давления в точке над атмосферным давлением.
Под вакуумом (рвак) в точке жидкости понимают недостаток абсолютного давления в точке до атмосферного.
Поверхность равного давления (поверхность уровня) — геометрическое место точек, в которых давление одинаково.
из основного дифференциального уравнения гидростатикиполучим уравнение поверхности уровня:
Поверхность, все точки которой имеют одинаковый потенциал U, называется эквипотенциальной поверхностью.
Следовательно, поверхность уровня одновременно является и эквипотенциальной поверхностью.