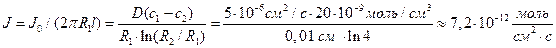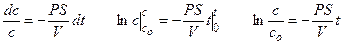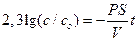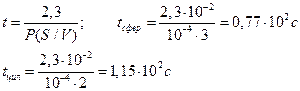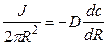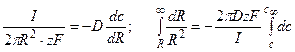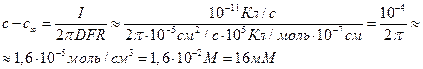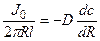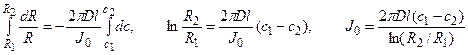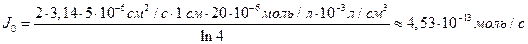концентрационный коэффициент каких ионов способствует диффузии
Концентрационный коэффициент каких ионов способствует диффузии
В разд. 69 мы упоминали, что единственной движущей силой как для диффузии, так и для миграции является градиент электрохимического потенциала компонентов. Поэтому можно ожидать, что подвижности и коэффициенты диффузии ионов связаны. Эта связь осуществляется уравнением Нернста-Эйнштейна
которое строго применимо лишь при бесконечном разбавлении, хотя его нарушение связано с приближенным характером уравнения потока (69-1). Величины 
в уравнении (75-1) при ненулевых концентрациях строго не определены; более глубокий анализ этого уравнения уместно отложить до гл. 12, где будут рассмотрены концентрированные растворы электролитов.
С учетом соотношения Нернста-Эйнштейна выражение (72-6) для коэффициента диффузии бинарного электролита приобретает вид
Часто можно встретить утверждение о том, что солевой мостик, используемый для устранения потенциалов жидкостного соединения, должен содержать соль с одинаковыми числами переноса катиона и аниона (потенциалами жидкостного соединения являются диффузионные потенциалы, возникающие при соединении двух растворов электролитов разных составов, см. гл. 6). Это утверждение можно пояснить с помощью уравнения Нернста-Эйнштейна. Для раствора единственной солц числа переноса номинально не зависят от концентрации (благодаря электронейтральности) и даются уравнением (72-12). Из уравнения (75-1) имеем
Равенство чисел переноса в сочетании с уравнением Нернста—Эйнштейна предполагает, что для симметричного электролита 
коэффициенты диффузии равны. Тогда можно
изменять концентрацию, так чтобы не возникали диффузионные потенциалы [уравнение (72-8) или (70-7)] (мы по-прежнему не имеем удовлетворительного ответа на вопрос о том, что происходит в местах контактов солевого мостика с обоими растворами, которые мы пытались соединить).
С другой стороны, с помощью соотношения Нернста-Эйнштейна уравнение (70-7) теперь можно записать в виде
В табл. 75-1 даны значения коэффициентов диффузии и подвижностей ионов. В литературе обычно не удается найти непосредственно значения подвижностей ионов. Вместо них приводятся эквивалентные ионные проводимости, связанные с подвижностями ионов равенством
Отсюда с помощью соотношения Нернста-Эйнштейна можно вычислить коэффициенты диффузии ионов:
Из табл. 75-1 видно, что большинство коэффициентов диффузии ионов находится около 
Исключения составляют ионы водорода и гидроксила, для которых 
равны 
Эквивалентная проводимость 
единственной соли является суммой соответствующих значений обоих ионов:
С проводимостью раствора величина 
связана соотношением
Значение 
составляет около 
за исключением кислот и оснований. Проводимость раствора получается умножением 
на эквивалентную концентрацию 
которая должна выражаться в 
чтобы к измерялась в 
Так, если должным образом учесть концентрационную зависимость 
то проводимость 
раствора 
(грубо—морской воды) будет составлять около 
Число переноса иона в растворе бинарной соли равно
Это число близко к 0,5 для всех электролитов, кроме кислот и
оснований, где 
может достигать 0,8 или падать до 0,2. Для растворов с избытком инертного электролита число переноса малой ионной добавки будет пропорционально ее концентрации и обратно пропорционально концентрации фонового электролита, и потому это число будет небольшим.
Таблица 75-1 (см. скан) Значения эквивалентных проводимостей и коэффициентов диффузии некоторых ионов в бесконечно разбавленных водных растворах при 25 °С
Эквивалентные ионные проводимости, как, например, те, что приведены в табл. 75-1, обычно определяются из измерений эквивалентной проводимости 
и чисел переноса 
для растворов единственной соли и последующей экстраполяцией полученных значений к бесконечному разбавлению. Тогда уравнения (75-7) и (75-9) дают 
Хорошее согласие получается, например, для ионов хлора, для которых величина 
определяется по
отдельности в растворах 
Коэффициенты диффузии, вычисленные по уравнению (75-2), также находятся в хорошем согласии со значениями, полученными в измерениях при сильном разбавлении.
Температурная зависимость ионных коэффициентов диффузии приближенно выражается соотношением
где 
вязкость раствора. Так, ионные коэффициенты диффузии и эквивалентные проводимости могут изменяться от 2 до 3% на один градус Цельсия. Это довольно сильная зависимость от температуры. Соотношение (75-10) можно также использовать для оценки концентрационной зависимости ионных коэффициентов диффузии.
Концентрационный коэффициент каких ионов способствует диффузии
В разд. 69 мы упоминали, что единственной движущей силой как для диффузии, так и для миграции является градиент электрохимического потенциала компонентов. Поэтому можно ожидать, что подвижности и коэффициенты диффузии ионов связаны. Эта связь осуществляется уравнением Нернста—Эйнштейна
которое строго применимо лишь при бесконечном разбавлении, хотя его нарушение связано с приближенным характером уравнения потока (69-1). Величины в уравнении (75-1) при ненулевых концентрациях строго не определены; более глубокий анализ этого уравнения уместно отложить до гл. 12, где будут рассмотрены концентрированные растворы электролитов.
С учетом соотношения Нернста—Эйнштейна выражение (72-6) для коэффициента диффузии бинарного электролита приобретает вид
Часто можно встретить утверждение о том, что солевой мостик, используемый для устранения потенциалов жидкостного соединения, должен содержать соль с одинаковыми числами переноса катиона и аниона (потенциалами жидкостного соединения являются диффузионные потенциалы, возникающие при соединении двух растворов электролитов разных составов, см. гл. 6). Это утверждение можно пояснить с помощью уравнения Нернста—Эйнштейна. Для раствора единственной соли, числа переноса номинально не зависят от концентрации (благодаря электронейтральности) и даются уравнением (72-12). Из уравнения (75-1) имеем
Равенство чисел переноса в сочетании с уравнением Нернста—Эйнштейна предполагает, что для симметричного электролита коэффициенты диффузии равны. Тогда можно изменять
концентрацию, так чтобы не возникали диффузионные потенциалы [уравнение (72-8) или (70-7)] (мы по-прежнему не имеем удовлетворительного ответа на вопрос о том, что происходит в местах контактов солевого мостика с обоими растворами, которые мы пытались соединить).
С другой стороны, с помощью соотношения Нернста—Эйнштейна уравнение (70-7) теперь можно записать в виде
В табл. 75-1 даны значения коэффициентов диффузии и подвижностей ионов. В литературе обычно не удается найти непосредственно значения подвижностей ионов. Вместо них приводятся эквивалентные ионные проводимости, связанные с подвижностями ионов равенством
Отсюда с помощью соотношения Нернста—Эйнштейна можно вычислить коэффициенты диффузии ионов:
Из табл. 75-1 видно, что большинство коэффициентов диффузии ионов находится около Исключения составляют ионы водорода и гидроксила, для которых D равны
Эквивалентная проводимость единственной соли является суммой соответствующих значений обоих ионов:
С проводимостью раствора величина связана соотношением
Значение составляет около за исключением кислот и оснований. Проводимость раствора получается умножением на эквивалентную концентрацию которая должна выражаться в чтобы измерялась в Так, если должным образом учесть концентрационную зависимость , то проводимость 0,6 М раствора (грубо-морской воды) будет составлять около
Число переноса иона в растворе бинарной соли равно
Это число близко к 0,5 для всех электролитов, кроме кислот и
оснований, где может достигать 0,8 или падать до 0,2. Для растворов с избытком инертного электролита число переноса малой ионной добавки будет пропорционально ее концентрации и обратно пропорционально концентрации фонового электролита, и потому это число будет небольшим.
Таблица 75-1. Значения эквивалентных проводимостей и коэффициентов диффузии некоторых ионов в бесконечно разбавленных водных растворах при 25 °С (см.скан)
Эквивалентные ионные проводимости, как, например, те, что приведены в табл. 75-1, обычно определяются из измерений эквивалентной проводимости и чисел переноса для растворов единственной соли и последующей экстраполяцией полученных значений к бесконечному разбавлению. Тогда уравнения (75-7) и (75-9) дают Хорошее согласие получается, например, для ионов хлора, для которых величина определяется по отдельности
в растворах Коэффициенты диффузии, вычисленные по уравнению (75-2), также находятся в хорошем согласии со значениями, полученными в измерениях при сильном разбавлении.
Температурная зависимость ионных коэффициентов диффузии приближенно выражается соотношением
где вязкость раствора. Так, ионные коэффициенты диффузии и эквивалентные проводимости могут изменяться от 2 до 3% на один градус Цельсия. Это довольно сильная зависимость от температуры. Соотношение (75-10) можно также использовать для оценки концентрационной зависимости ионных коэффициентов диффузии.
Диффузия ионов и неэлектролитов
Диффузия представляет собой спонтанное движение растворенного вещества в сторону понижения концентрации. Диффузионные законы определяют движение незаряженных веществ в объеме (на любых расстояниях при отсутствии конвекции), перенос ионов в неперемешиваемых слоях у поверхности мембран, а также движение ионов на малых расстояниях.
Формула Стокса–Эйнштейна связывает коэффициент диффузии D с температурой T, вязкостью среды η и радиусом диффундирующих частиц r (k – константа Больцмана). Например, вязкость воды при 20°С составляет ηH2O= 10 –3 Па∙с (1 Па = 1 Н/м 2 ).
(4.1)
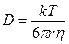
Пользуясь (4.1), можно оценить коэффициент диффузии в воде для малых молекул с радиусом
0,2 нм (10 –5 см 2 /с) или для молекул другого размера. На движение ионов в растворе влияет электрическое поле. Коэффициент диффузии иона зависит от его заряда (z):
, (4.2)
(4.3)
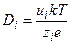
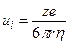
Подвижность численно равна скорости движения ионов (см/с) при напряженности поля 1 В/см.
Законы Фика описывают скорость диффузии вещества, а также пространственное распределение концентрации диффундирующего вещества в различные моменты времени.
Первый закон Фика связывает поток вещества J с коэффициентом диффузии D и градиентом концентрации (dc/dx). Размерность потока – моль∙см –2 ∙с –1 ).
(4.4)
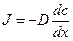
В случае диффузии через тонкую мембрану
, (4.5)
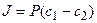
где P=Dg/h – проницаемость, h – толщина мембраны, g – коэффициент распределения вещества между водной и липидной фазами, а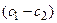 
– разность концентраций диффундирующего вещества в объемных фазах по разные стороны мембраны.
Второй закон Фика описывает направление изменений концентрации вещества во времени (dc/dt) в зависимости от знака второй производной (d 2 c/dx 2 ), определяющей вогнутость или выпуклость профиля концентрации по координате x:
(4.6)
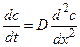
Из (4.6) в частности следует, что в случае одномерной стационарной диффузии (т.е. при dc/dt=0) профиль концентрации линеен: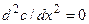 
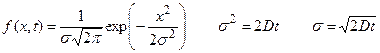
. В общем случае одномерной диффузии пространственно-временное распределение вещества описывается нормальным распределением Гаусса:
(4.7)
где x – координата, f(x,t) – функция распределения, σ – среднеквадратичное отклонение для нормального распределения вещества относительно исходной точки при x = 0, σ 2 – дисперсия, а t – время. Область, расположенная между координатами ±σ, содержит более 68% от общего количества диффундирующего вещества. Согласно уравнению Эйнштейна, величина σ, обозначаемая также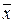 
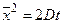
или ‹x›, служит мерой расстояния, на которое распространяется диффундирующее вещество за определенный промежуток времени t:
, (4.8)
где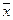 
– среднеквадратичное отклонение (диффузионная длина).
Пример 4.1. После инъекции в клетку некоторого вещества до концентрации co, клетку отмывают средой, не содержащей этого вещества. Какое время инкубации необходимо, чтобы внутренняя концентрация вещества понизилась в 10 раз, если проницаемость мембраны для этого вещества составляет 10 –4 см/с? Решить задачу для клетки сферической формы с диаметром 200 мкм и для цилиндрической клетки с диаметром 200 мкм и длиной 1 см.
Решение: При записи первого закона Фика учтем, что диффузия происходит через тонкую мембрану и, что концентрация во внешнем растворе равна нулю.
где с – концентрация вещества в клетке в момент времени t. Зная поток вещества через мембрану и геометрию клетки (площадь поверхности S и объем V), можно выразить изменение внутренней концентрации dc за промежуток времени dt:
.
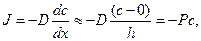
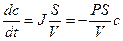
Решение этого дифференциального уравнения описывает кинетику изменения концентрации вещества внутри клетки:
, где 
.
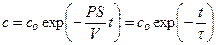
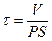
Уравнение решают методом разделения переменных и интегрирования по времени от нуля до t при соответствующем изменении концентрации от co до c.
Для ответа на вопрос задачи удобно перейти к десятичным логарифмам:
Отношение S/V определяется геометрией клетки. Для сферы и цилиндра оно составляет соответственно
и 
.
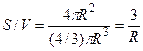
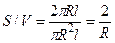
С учетом условия задачи c/co = 0,1 и R = 0,01 см, находим искомое время t:
Аналогичный подход используется для случаев, когда в момент времени t = 0 в наружный раствор добавляют проникающее вещество, которое начинает поступать внутрь клетки, причем наружная концентрация остается постоянной (co = const) из-за большого объема среды по сравнению с объемом клеток. В таком опыте моменту времени t = 0 соответствует внутренняя концентрация с = 0, а произвольному моменту времени t соответствует внутренняя концентрация с. В этом случае интегрирование дифференциального уравнения приводит к следующему решению:
.
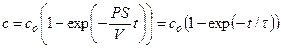
Пример 4.2. Предположим, что через калиевый канал с устьем R = 10 Å протекает ток I силой 10 пА (рис. 4.1.). При этом концентрация К + в устье повышается по сравнению с объемом раствора. Найти концентрацию в области устья канала, если концентрация К + в объеме составляет 10 мМ. При расчете принять, что коэффициент диффузии К + в воде
Решение: На выходе из канала суммарный поток переносимых ионов диффундирует во всех направлениях, ограничиваемых полусферой. Выделим элемент поверхности полусферы и запишем поток через единицу поверхности, пользуясь первым законом Фика.
Суммарный поток вещества J связан с электрическим током I соотношением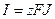 
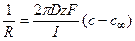
, где F – число Фарадея. Отсюда получим
, где z =1
Следовательно, перепад концентрацией между устьем канала и объемом раствора составит
Соответственно, концентрация в устье канала cx составит 26 мМ.
Пример 4.3. Концентрация Са 2+ в питательном растворе на расстоянии 300 мкм от поверхности корня составляет 100 мкМ, а у поверхности корня с диаметром 200 мкм – 80 мкМ. Оценить диффузионный поток Са 2+ к поверхности корня на 1 см его длины (моль·с –1 ), а также поток Са 2+ на единицу поверхности корня (моль·см –2 ·с –1 ) в предположении, что коэффициент диффузии D = 5·10 –6 см 2 /с.
Решение: Обозначим суммарный диффузионный поток для сегмента корня длиной l символом J0. Поток Са 2+ направлен радиально из объема среды к центру корня. Поток через единичный участок цилиндрической поверхности неперемешиваемого слоя на расстоянии R от центра корня составит J0/(2πRl). Запишем уравнение первого закона Фика в радиальных координатах:
Решая уравнение, находим формулу для расчета потока по концентрациям на разном удалении от центра корня (концентрации с1 и с2 для радиальных расстояний R1 и R2).
В расчете на единицу поверхности корня поток составит
.