колебания поршня в двигателе внутреннего сгорания могут служить примером каких колебаний
Колебания поршня двигателя внутреннего сгорания могут служить примером
4 такта работы двигателя внутреннего сгорания
Прежде, чем перейти непосредственно к работе двигателя отметим основные элементы его конструкции, это поможет правильно понять описание его работы.
Элементы конструкции ДВС
Цикл работы двигателя
Основные элементы конструкции двигателя определены, теперь можно разобраться в работе двигателя, как упоминалось ранее цикл его работы состоит из четырех тактов, рассмотрим подробнее каждый из них.
Такт 1
Чтобы двигатель мог, что то сжечь, надо сначала этим чем-то его заправить. В ДВС это смесь воздуха и топлива. При движении поршня вниз объем рабочей камеры увеличивается, значит давление в ней падает. Клапаны соединяющие рабочую камеры с впускным коллектором открываются и воздух заполняет ее. Топливо распыляется с помощью форсунки.
Такт 2
Полученную смесь надо сжать, чтобы при воспламенении она расширилась и переместила поршень. Для осуществления сжатия поршень нужно переместить вверх, клапаны в этот момент должны быть закрыты.
Такт 3
На третьем этапе свеча дает искру, которая воспламеняет смесь, она нагревается и расширяется, толкая поршень вниз. Поршень вращает коленвал.
Такт 4
От продуктов горения нужно избавиться. Для этого открываются клапаны со стороны выпускного коллектора, поршень движется вверх вытесняя газы в выхлопную систему.
После 4 такта вновь наступает первый.
Количество поршней
Таким образом поршень только на третьем этапе вращал коленчатый вал, а на всех остальных наоборот коленвал перемещал поршень. Но откуда на валу возьмется энергия для вращения вала. Можно использовать не один поршень, а несколько. Пожалуй,самым логичным решением будет установка четырех поршней (хотя их может быть и 3, и 6, и 12). Если в двигателе 4 поршня, то каждый из них в один момент находится на разных этапах:
Для обеспечения плавной работы на валу двигателя может быть установлен маховик.
Источник статьи: http://zen.yandex.ru/media/id/5a1e4c52ad0f22bbdcdd408c/4-takta-raboty-dvigatelia-vnutrennego-sgoraniia-5fa8e4bb3a59d85105f58a7a
Механические колебания
теория по физике 🧲 колебания и волны
Колебательное движение очень распространено. Заставить колебаться можно любое тело, если приложить к нему силу — однократно или постоянно. К примеру, если подтолкнуть качели, они начнут качаться вперед-назад, и такое движение будет приблизительно повторяться до тех пор, пока качели полностью не остановятся.
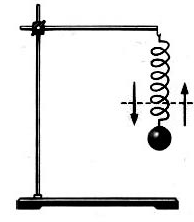
Другой пример колебательного движения — тело, подвешенное к пружине. Если его потянуть вниз и отпустить, то за счет сил упругости оно сначала поднимется вверх, а затем снова опустится вниз, затем движения вверх-вниз будут повторяться. Со временем они прекратятся под действием силы сопротивления воздуха.
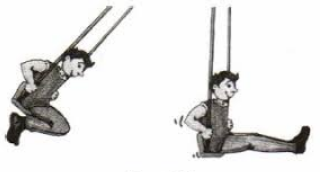
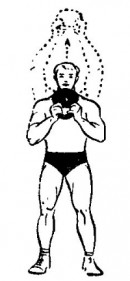
Колебаниями можно назвать даже движение гири, которую поднимается тяжелоатлет вверх, а затем опускает в низ. При этом он будет прикладывать к гире силу постоянно. Гиря будет колебаться до тех пор, пока к нему будет прикладываться эта сила.
Колебания — это движения, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания — это колебательные движения, совершаемые физическим телом в механической системе.
Механическая система — совокупность материальных точек (тел), движения которых взаимосвязаны между собой.
Какими бывают колебания?
Напомним, что в механической системе выделяют два вида сил:
Свободные колебания
Свободные колебания — колебания, происходящие в системе под действием внутренних сил после того, как эта система выведена из положения равновесия.
Колебательная система — механическая система, в которой возможно совершение свободных колебаний.
Свободные колебания в колебательной системе могут возникнуть только при наличии двух условий:
Примеры свободных колебаний:
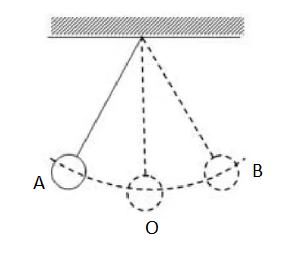
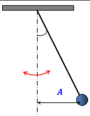
Примером колебательной системы также служит математический маятник — материальная точка, подвешенная на невесомой нерастяжимой нити. В действительности такого маятника не существует. Это идеализированная модель реального маятника, примером которого служит тяжелый шарик, подвешенный на длинной нити. В этом случае размером шарика и растяжением нити можно пренебречь.
В колебательную систему математического маятника входят:
В положении равновесия (точка О) шарик висит на нити и покоится. Если его отклонить от положения равновесия до точки А и отпустить, под действием силы тяжести шарик приблизится к положению равновесия. Так как к этому моменту шарик обретет скорость, он не сможет остановиться и приблизится к точке В. Затем он снова вернется в точку А через положение равновесия в точке О. Шарик будет колебаться, пока не затухнут под действием возникающей силы сопротивления воздуха.
Вынужденные колебания
Вынужденные колебания — колебания тел под действием внешних периодически изменяющихся сил.
Примерами вынужденных колебаний служат:
Затухающие и незатухающие колебания
Затухающие колебания — колебания, которые со временем затухают. При этом максимальное отклонение тела от положения равновесия с течением времени уменьшается.
Колебания затухают под действием сил, препятствующих колебательному движению. Так, шарик в сферической чаше перестает колебаться под действием силы трения. Математический маятник и качели перестают совершать колебательные движения за счет силы сопротивления воздуха.
Все свободные колебания являются затухающими, так как всегда присутствует трение или сопротивление среды.
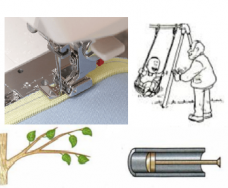
Незатухающими колебаниями могут быть только те, которые совершаются под действием периодической внешней силы (вынужденные колебания). Так, ветка будет раскачиваться до тех пор, пока дует ветер. Когда он перестанет дуть, колебания ветки со временем затухнут. Иголка швейной машинки будет совершать колебательные движения до тех пор, пока швея вращает ручку привода. Когда она перестанет это делать, иголка сразу остановится.
Динамика колебательного движения
Для того чтобы описать количественно колебания тела пол действием силы упругости пружины или колебания шарика, подвешенного на нити, воспользуемся законами механики Ньютона.
Уравнение движения тела, колеблющегося под действием сил упругости
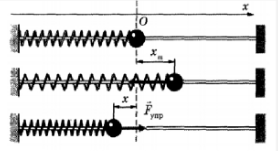
Рассмотрим колебательное движение шарика, вызванное силой упругости, возникшей при растяжении горизонтальной пружины вдоль оси Ох.
Согласно II закону Ньютона произведение массы тела на ускорение равно равнодействующей всех сил приложенных к телу. Поскольку сила трения пренебрежимо мала, мы можем считать, что в этой механической системе действует единственная сила — сила упругости. Учтем, что шарик колеблется вдоль одной прямой, и выберем одномерную систему координат Ох. Тогда:
Согласно закону Гука, проекция сила упругости прямо пропорциональная смещению шарика из положения равновесия (точки О). Смещение равно координате x шарика, причем проекция силы и координаты имеют разные знаки. Это связано с тем, что сила упругости всегда направлена к точке равновесия, в то время как расстояние от этой точки во время движения увеличивается в обратную сторону. Отсюда делаем вывод, что сила упругости равна:
Тогда уравнение движения шарики принимает вид :
Пример №1. Груз массой 0,1 кг прикрепили к пружине школьного динамометра жесткостью 40 Н/м. В начальный момент времени пружина не деформирована. После того, как груз отпускают, возникают колебания. Чему равна максимальная скорость груза?
Максимальной скорости груз достигнет при максимальном его отклонении от положения равновесия — в нижней точке траектории. Учтем, что тело движется вниз под действием силы тяжести. Но в то же время на него действует сила упругости, которая возникает в пружине и нарастает до тех пор, пока не становится равной по модулю силе тяжести. Применив III закон Ньютона получим:
где y m a x — максимальное отклонение груза от положения равновесия. В этой точке скорость тела будет максимальная. Для нахождения этой величины используем формулу из кинематики:
Начальная скорость равна нулю. Отсюда:
Максимальная скорость равна:
Уравнение движения математического маятника
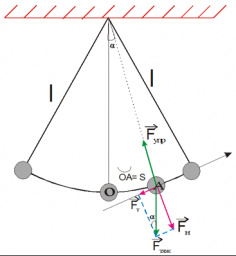
Ниже на рисунке представлен математический маятник. Если мы выведем из положения равновесия шарик и отпустим, возникнет две силы:
При колебаниях шарика также будет возникать сила сопротивления воздуха. Но так как она очень мала, мы будем ею пренебрегать.
Чтобы описать динамику движения математического маятника, удобно силу тяжести разложить на две составляющие:
Причем компонента → F τ направлена перпендикулярно нити, а → F n — вдоль нее.
Компонента → F τ представляет собой проекцию силы тяжести в момент, когда нить маятника отклонена от положения равновесия (точки О) на угол α. Следовательно, она равна:
Знак «–» мы здесь поставили по той причине, что компоненты силы тяжести → F τ и α имеют противоположные знаки. Ведь если отклонить шарик на угол α>0, то составляющая → F τ будет направлена в противоположную сторону, так как она будет пытаться вернуть шарик в положение равновесия. И ее проекция будет отрицательной. Если же шарик отклонить на угол α → F τ будет направлена в обратную сторону. В этом случае ее проекция будет положительной.
Разделим обе части выражения на массу шарика m и получим:
Внимание! Чтобы перевести градусы в радианы, нужно умножить градусы на число π и поделить результат на 180. К примеру 2 о = 2∙3,14/180 рад., или 2 о = 0,035 рад.
При малом отклонении также дугу ОА мы можем принять за длину отрезка OA, который мы примем за s. Тогда угол α будет равен отношению противолежащего катета (отрезка s) к гипотенузе (длине нити l):
Это уравнение похоже на то уравнение, которое мы получили для описания колебательного движения шарика под действием силы упругости. И оно также позволяет сделать вывод, что ускорение прямо пропорционально координате.
При отклонениях на малый угол мы можем пользоваться следующей формулой:
Чтобы найти длину нити, нужно выразить угол α в радианах:
Основные характеристики колебательного движения
Амплитуда — максимальное отклонение тела от положения равновесия. Обозначается буквой A, иногда — xmax. Единиц измерения — метр (м).
Период — время совершения одного полного колебания. Обозначается буквой T. Единица измерения — секунда (с).
Период и частота колебаний связаны между собой следующей формулой:
Период колебаний также можно вычислить, зная количество совершенных колебаний N за время t:
Поскольку частота — это величина, обратная периоду колебаний, ее можно выразить в виде:
Пример №3. Определить частоту колебаний груза, если суммарный путь, который он прошел за 2 секунды под действием силы упругости, составил 1 м. Амплитуда колебаний равна 10 см.
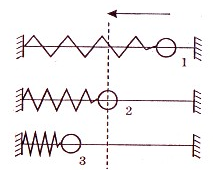
Во время одного колебания груз проходит расстояние, равное 4 амплитудам. Посмотрите на рисунок. Положение равновесия соответствует состояние 2. Чтобы совершить одно полное колебание, сначала груз отводят в положение 1. Когда его отпускают, он проходит путь 1–2 и достигает положения равновесия. Этот путь равен амплитуде колебаний. Затем он продолжает движение до состояния 3. И в это время он проходит расстояние 2–3, равное еще одной амплитуде колебаний. Чтобы вернуться в исходное положение (состояние 1), нужно снова проделать путь в обратном направлении: сначала 3–2, затем 2–1.
Следовательно, количество колебаний равно отношению пройденного пути к амплитуде, помноженной на 4:
Так как мы знаем, что эти колебания совершались в течение 2 секунд, для вычисления частоты мы можем использовать формулу:
В таблице представлены данные о положении шарика, колеблющегося вдоль оси Ох, в различные моменты времени.
Каков период колебаний шарика?
Алгоритм решения
Из таблицы видно, что амплитуда колебаний равна 15 мм. Следовательно, максимальное отклонение в противоположную сторону составляет –15 мм. Расстояние между двумя максимальными отклонениями от положения равновесия шарика равно половине периода колебаний. Этим значения в таблице соответствует время 1 и 3 секунды соответственно. Следовательно, разница между ними — половина периода. Тогда период будет равен удвоенной разнице во времени:
T = 2 ( t 2 − t 1 ) = 2 ( 3 − 1 ) = 4 ( с )
pазбирался: Алиса Никитина | обсудить разбор | оценить
Массивный груз, подвешенный к потолку на пружине, совершает вертикальные свободные колебания. Пружина всё время остается растянутой. Как ведут себя потенциальная энергия пружины, кинетическая энергия груза, его потенциальная энергия в поле тяжести, когда груз движется вверх к положению равновесия?
Для каждой величины определите соответствующий характер изменения:
| 1) | увеличивается |
| 2) | уменьшается |
| 3) | не изменяется |
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
Алгоритм решения
Потенциальная энергия пружины определяется формулой:
где k — коэффициент жесткости пружины, а x — ее удлинение. Величина x была максимальной в нижней точке траектории. Когда пружина начинает сжиматься, она уменьшается. Так как потенциальная энергия зависит от квадрата x прямо пропорционально, то при уменьшении этой величины потенциальная энергия пружины тоже уменьшается.
Кинетическая энергия тела определяется формулой:
В нижней точке траектории скорость шарика была равна нулю. Но к этому времени потенциальная энергия пружины достигла максимума. Она начинает с ускорением поднимать шарик вверх, сжимаясь. Следовательно, скорость растет. Так как кинетическая энергия зависит от квадрата скорости тела прямо пропорционально, то при увеличении скорости этой величины кинетическая энергия шарика тоже увеличивается.
Потенциальная энергия тел в поле тяжести земли определяется формулой:
Масса и ускорение свободного падения шарика — постоянные величины. Следовательно, потенциальная энергия зависит только от расстояния до поверхности земли. Когда пружина поднимает шарик, расстояние между ним и землей увеличивается. Так как потенциальная энергия зависит от расстояния прямо пропорционально, то при его увеличении потенциальная энергия шарика тоже растет.
pазбирался: Алиса Никитина | обсудить разбор | оценить
В таблице представлены данные о положении шарика, прикреплённого к пружине и колеблющегося вдоль горизонтальной оси Ох, в различные моменты времени.
Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.
А) Потенциальная энергия пружины в момент времени 1,0 с максимальна.
Б) Период колебаний шарика равен 4,0 с.
В) Кинетическая энергия шарика в момент времени 2,0 с минимальна.
Г) Амплитуда колебаний шарика равна 30 мм.
Д) Полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна.
Алгоритм решения
Согласно утверждению «А», потенциальная энергия пружины в момент времени 1,0 с максимальна. Потенциальная энергия пружины максимальна, когда она отклоняется от положения равновесия на максимальную возможную величину. Из таблицы видно, что в данный момент времени ее отклонение составило 15 мм, что соответствует амплитуде колебаний (наибольшему отклонению от положения равновесия). Следовательно, утверждение «А» — верно.
Согласно утверждению «Б», период колебаний шарика равен 4,0 с. Один период колебаний включает в себя 4 фазы. В течение каждой фазы шарик на пружине проделывает путь, равный амплитуде. Следовательно, мы можем найти период колебаний, умножив время одной фазы на 4. В момент времени t = 0 с, шарик находился в положении равновесия. Первый раз он отклонился на максимальную величину (15 мм) в момент времени t = 1,0 с. Значит, период колебаний равен 1∙4 = 4 с. Следовательно, утверждение «Б» — верно.
Согласно утверждению «В», кинетическая энергия шарика в момент времени 2,0 с минимальна. В этот момент времени, согласно данным таблицы, шарик проходит положение равновесия. В этом положении скорость шарика всегда максимальна. Поэтому кинетическая энергия, которая зависит от квадрата скорости прямо пропорционально, минимальной быть не может. Следовательно, утверждение «В» — неверно.
Согласно утверждению «Г», амплитуда колебаний шарика равна 30 мм. Амплитуда колебаний — есть расстояние от положения равновесия до точки максимального отклонения шарика. В данном случае оно равно 15 мм. Следовательно, утверждение «Г» — неверно.
Согласно утверждению «Д», полная механическая энергия маятника, состоящего из шарика и пружины, в момент времени 3,0 с минимальна. Полная механическая энергия колебательной системы — это совокупность кинетической и потенциальной энергий. И при отсутствии сил трения она остается величиной постоянной. Она лишь превращается из одного вида энергии в другую. Следовательно, утверждение «Д» — неверно.
pазбирался: Алиса Никитина | обсудить разбор | оценить
Колебания поршня в двигателе внутреннего сгорания могут служить примером каких колебаний
Периодические знакопеременные относительные угловые смешения элементов коленчатого вала, происходящие под действием переменных по времени и сдвинутых по фазе крутящих моментов на отдельных кривошипах (рис. 8.1), называются крутильными колебаниями коленчатого вала.
По определению они являются колебаниями вынужденными. Их параметры зависят как от упругомассовых и диссипативных характеристик крутильной системы, так и от характеристик силовых факторов, возбуждающих колебания.
К основным характеристикам колебательной системы относятся:
диссипативные характеристики, характеризующие необратимые неупругие потери колебательной энергии в крутильной системе; обычно они оцениваются коэффициентом потерь, представляющим собой отношение количества энергии, необратимо теряемой в крутильной системе, к количеству энергии, вносимой в нее силовыми факторами.
Факторами, возбуждающими колебания крутильной системы, являются крутящие моменты (/) на отдельных кривошипах, которые идентичны по форме временной реализации и отличаются друг от друга фазовым сдвигом, определяемым порядком работы и углом чередования рабочих ходов в двигателе.
При вынужденных колебаниях наибольшая их интенсивность наблюдается на режиме, называемом резонансным, когда одна из множества частот собственных колебаний системы совпадает с частотой одной из гармоник крутящего момента.
Следует отметить, что крутильная система коленчатого вала относится к колебательным системам с высокой «добротностью», т. е. имеет очень низкий уровень внутренних потерь. Для таких систем характерны следующие особенности:
Применительно к задаче анализа крутильных колебаний следование этим принципам означает, что:
в расчет принимаются только режимы резонансных колебаний;
Колебания каких из приведенных ниже тел будут свободными : а)поршень в цилиндре двигателя ; б)игла швейной машины ; в)ветка дерева после того, как с неё слетела птица ; г)струна музыкального инструмен?
Колебания каких из приведенных ниже тел будут свободными : а)поршень в цилиндре двигателя ; б)игла швейной машины ; в)ветка дерева после того, как с неё слетела птица ; г)струна музыкального инструмента ; д)чаши рычажных весов ; е)мембрана телефона при разговоре.
В)ветка дерева после того, как с неё слетела птица ;
В каких из приведенных ниже случаев тело можно считать материальной точкой?
В каких из приведенных ниже случаев тело можно считать материальной точкой?
Какие из перечисленных ниже колебаний являются вынужденными?
Какие из перечисленных ниже колебаний являются вынужденными?
Колебание струны гитары 3.
Колебания чашек рычажных весов.
Можно ли назвать свободными колебания :
Б)струны скрипки, звучащей под смычком?
В)грузовика, едущего по ухабам?
Г)иглы швейной машины?
Е)листьев на деревьях?
К каким колебаниям — свободным или вынужденным — относятся следующие явления : движение поршня в двигателе внутреннего сгорания ; вибрация стола, вызванная падением на него тяжелого предмета ; перемещ?
К каким колебаниям — свободным или вынужденным — относятся следующие явления : движение поршня в двигателе внутреннего сгорания ; вибрация стола, вызванная падением на него тяжелого предмета ; перемещение иглы в работающей швейной машине ; вертикальные перемещения поплавка на волнах ; колебания струны, возникшие после однократного воздействия?
1. Какое из перечисленных ниже движений является механическим колебанием?
1. Какое из перечисленных ниже движений является механическим колебанием?
А) движение груга на пружине б)движение мяча падающего на землю в)движение иглы швейной машины.
(возможно несколько вариантов) 2.
Какиеиз перечисленных ниже колебаний являются свободными?
А) колебания груза, подвешенного к пружине, после однократного его отклонения от положения равновесия.
Б)колебания диффузора громкоговорителя во время работы приемника в) колебания груза на нити, один раз отведенного от положения равновесия и отпущенного.
Что такое рычажные весы?
Определите период колебания иглы.
Мощность двигателя швейной машины 62?
Мощность двигателя швейной машины 62.
Какую работу он совершил за 20 мин.
На рычажных весах уравновешены камень и кусок дерева?
На рычажных весах уравновешены камень и кусок дерева.
Нарушится ли равновесие если весы перенести на луну?
Мощный двигатель швейной машины 40 Вт?
Мощный двигатель швейной машины 40 Вт.
Какую работу он совершит за 5 минут?
1. Какие частицы являются носителями электрического тока в газах? Г) Электроны, положительно отрицательно заряженные ионы. 2. Какими частицами может создаваться электрический ток в вакууме? А. только электронами 3. В каком случае вокруг движущего..
Мельчайшая частица химического элемента это атом. Например, у химического элемента водорода мельчайшей частицей будет не молекула водорода, а атом водорода. А молекула водорода будет мельчайшей частицей вещества водород. Мельчайшими частицами атом..
I = 2. 4cos6280t ; ампитудное значение Im = 2. 4 ; действующее значение Id = Im / √2 = 2. 4 / √2≈1. 70 ; ω = 6280 2πν = 6280 частота 6280 / 2π≈6280 / 6, 28 = 1000 Гц период Т = 1 / ν = 0, 001 сек.
Да, если доза больше допустимой.