какую точку называют критической точкой функции
Построение графиков функций
Понятие функции
Функция — это зависимость y от x, где x является переменной или аргументом функции, а y — зависимой переменной или значением функции.
Задать функцию значит определить правило, в соответствии с которым по значениям независимой переменной можно найти соответствующие ее значения. Вот, какими способами ее можно задать:
Область определения — множество х, то есть область допустимых значений выражения, которое записано в формуле.
Например, для функции вида 
Область значений — множество у, то есть это значения, которые может принимать функция.
Например, естественная область значений функции y = x² — это все числа больше либо равные нулю. Можно записать вот так: Е (у): у ≥ 0.
Понятие графика функции
Графиком функции y = f(x) называется множество точек (x; y), координаты которых связаны соотношением y = f(x). Само равенство y = f(x) называется уравнением данного графика.
График функции — это множество точек (x; y), где x — это аргумент, а y — значение функции, которое соответствует данному аргументу.
Проще говоря, график функции показывает множество всех точек, координаты которых можно найти, просто подставив в функцию любые числа вместо x.
Для примера возьмём самую простую функцию, в которой аргумент равен значению функции, то есть y = x.
В этом случае нам не придётся вычислять для каждого аргумента значение функции, так как они равны, поэтому у всех точек нашего графика абсцисса будет равна ординате.
Если мы последовательно от наименьшего значения аргумента к большему соединим отмеченные точки, то у нас получится прямая линия. Значит графиком функции y = x является прямая. На графике это выглядит так:
Надпись на чертеже y = x — это уравнение графика. Ставить надпись с уравнением на чертеже удобно, чтобы не запутаться в решении задач.
Важно отметить, что прямая линия бесконечна в обе стороны. Хоть мы и называем часть прямой графиком функции, на самом деле на чертеже изображена только малая часть графика.
Исследование функции
Важные точки графика функции y = f(x):
Стационарные точки — точки, в которых производная функции f(x) равна нулю.
Критические точки — точки, в которых производная функции f(x) равна нулю либо не существует. Стационарные точки являются подмножеством множества критических точек.
Экстремум в математике — максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.
Нули функции — это значения аргумента, при которых функция равна нулю.
Асимптота — прямая, которая обладает таким свойством, что расстояние от точки графика функции до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат. По способам их отыскания выделяют три вида асимптот: вертикальные, горизонтальные, наклонные.
Функция непрерывна в точке k, если предел функции в данной точке равен значению функции в этой точке:
Если функция f(x) не является непрерывной в точке x = a, то говорят, что f(x) имеет разрыв в этой точке.
Если нам нужно построить график незнакомой функции, когда заранее невозможно представить вид графика, полезно применять схему исследования свойств функции. Она поможет составить представление о графике и приступить к построению по точкам.
Схема построения графика функции:
У нас есть отличные онлайн занятия по математике для учеников с 1 по 11 классы! Приходи на пробное занятие с нашими лучшими преподавателями!
Построение графика функции
Чтобы понять, как строить графики функций, потренируемся на примерах.
Задача 1. Построим график функции
Упростим формулу функции:
Задача 2. Построим график функции
Выделим в формуле функции целую часть:
График функции — гипербола, сдвинутая на 3 вправо по x и на 2 вверх по y и растянутая в 10 раз по сравнению с графиком функции
Выделение целой части — полезный прием, который применяется в решении неравенств, построении графиков и оценке целых величин.
Задача 3. По виду графика определить знаки коэффициентов общего вида функции y = ax2 + bx + c.
Вспомним, как параметры a, b и c определяют положение параболы.
Ветви вниз, следовательно, a 0.
Точка пересечения с осью Oy — c = 0.
Координата вершины 
Ветви вниз, следовательно, a 0.
Координата вершины 
| x | y |
| 0 | -1 |
| 1 | 2 |
| x | y |
| 0 | 2 |
| 1 | 1 |
| x | y |
| 0 | 0 |
| 1 | 2 |
k = 2 > 0 — угол наклона к оси Ox острый, B = 0 — график проходит через начало координат.
Задача 5. Построить график функции
Это дробно-рациональная функция. Область определения функции D(y): x ≠ 4; x ≠ 0.
Нули функции: 3, 2, 6.
Промежутки знакопостоянства функции определим с помощью метода интервалов.
Вертикальные асимптоты: x = 0, x = 4.
Если x стремится к бесконечности, то у стремится к 1. Значит, y = 1 — горизонтальная асимптота.
Вот так выглядит график:
Задача 6. Построить графики функций:
б)
г)
д)
Когда сложная функция получена из простейшей через несколько преобразований, то преобразования графиков можно выполнить в порядке арифметических действий с аргументом.
а)
Преобразование в одно действие типа f(x) + a.
Сдвигаем график вверх на 1:
б)
Сдвигаем график вправо на 1:
Сдвигаем график вправо на 1:
Сдвигаем график вверх на 2:
г)
Преобразование в одно действие типа
Растягиваем график в 2 раза от оси ординат вдоль оси абсцисс:
д)
Чтобы выполнить преобразования, посмотрим на порядок действий: сначала умножаем, затем складываем, а уже потом меняем знак. Чтобы применить умножение ко всему аргументу модуля в целом, вынесем двойку за скобки в модуле.


Сжимаем график в два раза вдоль оси абсцисс:

Сдвигаем график влево на 1/2 вдоль оси абсцисс:

Отражаем график симметрично относительно оси абсцисс:

Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Какую точку называют критической точкой функции
Точки максимума и минимума функции называются точками экстремума (рис. 3.5).
Теорема 3.15 (необходимое условие существования точек экстремума функции одной переменной). Если дифференцируемая функция y = f ( x ) имеет экстремум в точке x 0, то её производная в этой точке равна нулю или не существует
Точки, в которых производная функции либо равна нулю, либо не существует, называют критическими точками 1-го рода.
Критические точки, в которых производная функции равна нулю, называются точками стационарности.
Для дальнейшего исследования критические точки помещают на числовую ось, которая делится этими точками на интервалы, после чего поверяют выполнение следующих достаточных условий.
Теорема 3.16 (достаточное условие возрастания и убывания функции одной переменной ). Если на некотором интервале ( a ; b ) функция y = f ( x ) дифференцируема и при этом ее производная 
Теорема 3.17 (достаточное условие существования точек экстремума функции ). Если функция y = f ( x ) непрерывна и дифференцируема в некоторой δ – окрестности критической точки x 0 и при переходе через нее производная 
Критические точки 1-го рода, в которых производная не существует, делятся на классы:
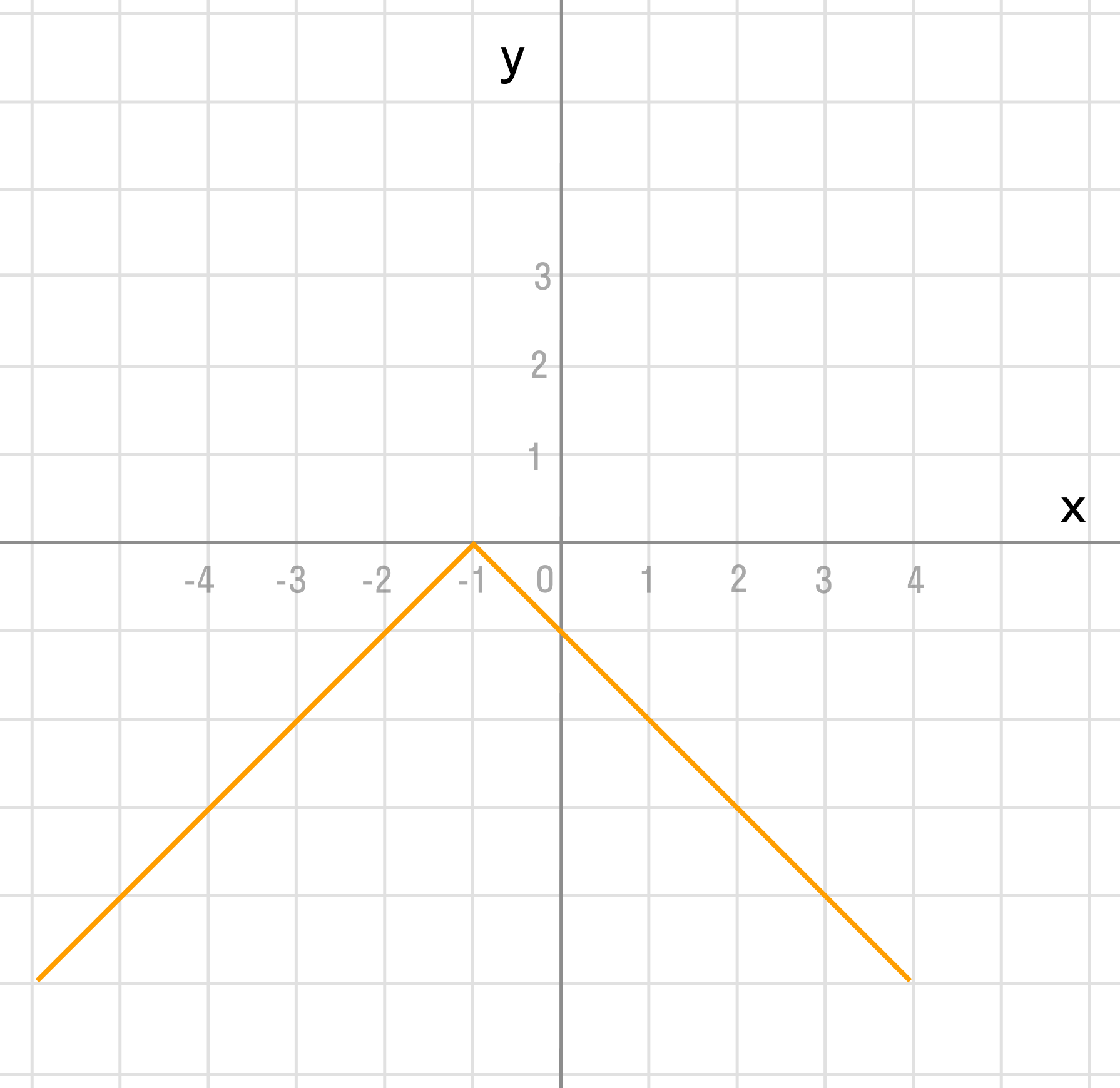
– точки, в которых функция непрерывна, но при выполнении теоремы 3.17 имеет в этих точках «острый» экстремум (угловые точки или точки излома) (рис. 3.6);
– точки, в которых функция непрерывна, но касательная в них к графику функции параллельна оси 0 y (угловой коэффициент такой касательной
– точки, в которых функция терпит разрыв (всегда переходят в класс критических точек 2-го рода).
Но проведенное таким образом исследование, не дает ответ на очень важный вопрос: как возрастает (убывает) функция – выпукло или вогнуто? Ответ на поставленный вопрос дает дальнейшее рассмотрение функции с помощью второй производной. Дадим ряд необходимых определений.
Функция называется выпуклой (выпуклой вверх) на некотором интервале ( a ; b ), если касательная, проведенная к графику функции в каждой точке этого интервала, лежит выше графика функции.
Точки, отделяющие участки выпуклости от участков вогнутости функции, называются ее точками перегиба (см. рис. 3.5).
Теорема 3.18 (необходимое условие существования точек перегиба функции ). Если дважды дифференцируемая функция y = f ( x ) имеет перегиб в точке x 0, то в этой точке вторая производная равна нулю или не существует
Точки, в которых вторая производная функции либо равна нулю, либо не существует, называют критическими точками 2-го рода.
Для дальнейшего исследования критические точки 2-го рода помещают на числовую ось, которая делится этими точками на интервалы, после чего поверяют выполнение следующих достаточных условий.
Теорема 3.19 (достаточное условие выпуклости и вогнутости функции). Если на некотором интервале ( a ; b ) функция y = f ( x ) дважды дифференцируема и при этом ее вторая производная 
Теорема 3.20 (достаточное условие существования точек перегиба функции). Если функция y = f ( x ) непрерывна и дважды дифференцируема в некоторой окрестности критической точки 2-го рода и при переходе через нее вторая производная меняет знак, то данная точка является точкой перегиба функции
Те критические точки функции, для которых достаточное условие 3.19 не выполняется, остаются просто критическими точками 2-го рода. Критические точки 2-го рода, в которых вторая производная не существует, делятся на классы:
– угловые точки (переходят из критических точек первого рода);
– точки, в которых функция терпит разрыв (в точках разрыва 2-го рода график функции имеет вертикальную асимптоту).
Для окончательного перечисления точек экстремума и перегиба функции необходимо найти их ординаты, после чего выписать указанные точки двумя координатами.
Для завершения исследования функции и построения графика необходимо проверить наличие у нее асимптот. Напомним, что асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат точки по кривой (рис. 3.8).
Асимптоты могут быть вертикальными, наклонными, горизонтальными.
Говорят, что прямая x = a является вертикальной асимптотой графика
Уравнение наклонной асимптоты ищем в виде y = kx + b (рис. 3.8).
Верно и обратное: если существуют конечные пределы (3.41) и (3.42), то прямая y = kx + b является наклонной асимптотой.
Если хотя бы один из пределов (3.41) или (3.42) не существует или равен бесконечности, то кривая y = f ( x ) наклонной асимптоты не имеет.
Примечание. Асимптоты графика функции y = f ( x ) при ∆ x →+∞ и ∆ x → – ∞ могут быть разными. Поэтому при нахождении пределов (3.41) и (3.42) следует отдельно рассматривать случай, когда ∆ x →+∞ и когда ∆ x → – ∞.
Таким образом, точка x =4 является для заданной функции точкой разрыва второго рода, а прямая x =4 – вертикальной асимптотой графика.
Результаты исследования заданной функции с помощью первой производной занесем в таблицу 3.1, основываясь на теоремах 3.16, 3.17.
Исследование функции с помощью первой производной
4. Исследуем функцию на выпуклость, вогнутость и точки перегиба с помощью второй производной, основываясь на теоремах 3.23, 3.24:
Исследование функции с помощью второй производной
Таким образом, прямая y = x +4 – наклонная асимптота графика.
Какую точку называют критической точкой функции
Определения:
Экстремумом называют максимальное или минимальное значение функции на заданном множестве.
Точка экстремума – это точка, в которой достигается максимальное или минимальное значение функции.
Точка максимума – это точка, в которой достигается максимальное значение функции.
Точка минимума – это точка, в которой достигается минимальное значение функции.
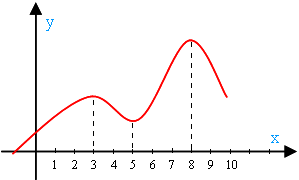
На рисунке в окрестности точки х = 3 функция достигает максимального значения (то есть в окрестности именно этой точки нет точки выше). В окрестности х = 8 она опять же имеет максимальное значение (снова уточним: именно в этой окрестности нет точки выше). В этих точках возрастание сменяется убыванием. Они являются точками максимума:
В окрестности точки х = 5 достигается минимальное значение функции (то есть в окрестности х=5 точки ниже нет). В этой точке убывание сменяется возрастанием. Она является точкой минимума:
Точки максимума и минимума являются точками экстремума функции, а значения функции в этих точках – ее экстремумами.
Точка xо является точкой максимума, если у нее существует окрестность, во всех точках которой f(x) меньше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с плюса на минус, то xо является точкой максимума.
Точка хо является точкой минимума, если у нее существует окрестность, во всех точках которой f(x) больше или равно f(xо):
Упрощенная формулировка : если в точке xо производная меняет знак с минуса на плюс, то xо является точкой минимума.
Критические и стационарные точки функции:
Внутренние точки области определения функции, в которых функция непрерывна, но производная не существует, называют критическими точками.
Внутренние точки области определения функции, при которых производная функции равна нулю, называются стационарными точками.
Необходимое условие экстремума:
Если xо – точка экстремума функции f (x), то в этой точке либо производная обращается в нуль (и это стационарная точка), либо производная не существует (критическая точка).
Достаточное условие экстремума:
Пусть xо – критическая точка. Если производная f ′(x) при переходе слева направо через точку xо меняет знак плюс на минус, то xо – точка максимума:
Если производная f ′(x) при переходе слева направо через точку xо меняет знак минус на плюс, то xо – точка минимума:
Если при переходе через критическую точку производная не меняет знак, то в точке xо экстремума нет.
На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].
Алгоритм исследования непрерывной функции y = f(x) на монотонность и экстремумы:
2) Найти стационарные (f ′(x) = 0) и критические (f ′(x) не существует) точки функции y = f(x).
3) Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
4) Сделать выводы о монотонности функции и ее точках экстремума.