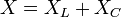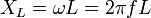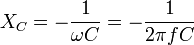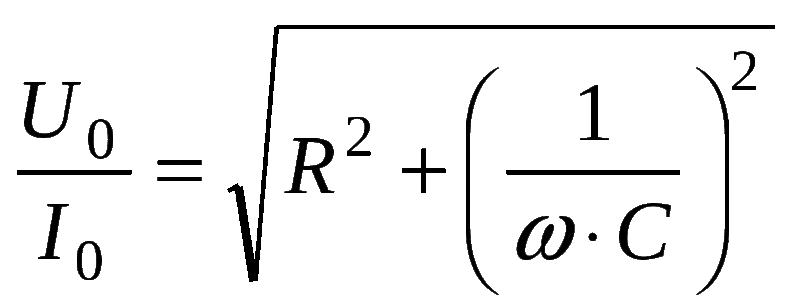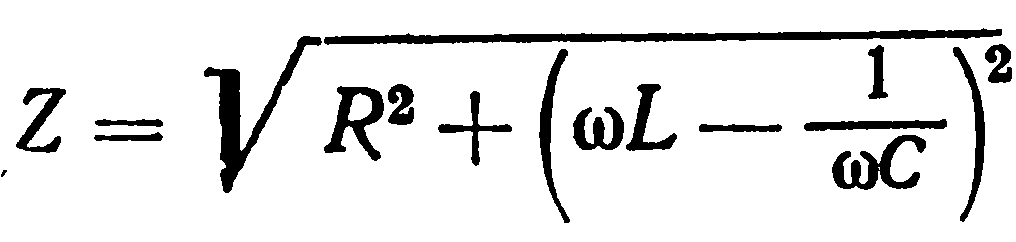какую размерность имеет емкостное сопротивление
Ёмкостное сопротивление
Реактивное сопротивление определяет мнимую часть импеданса:
В зависимости от величины X какого-либо элемента электрической цепи, говорят о трёх случаях:
Величина реактивного сопротивления может быть выражена через величины индуктивного и ёмкостного сопротивлений:
Индуктивное сопротивление (XL) обусловлено возникновением ЭДС самоиндукции. Электрический ток создает магнитное поле. Изменение тока, и как следствие изменение магнитного поля, вызывает ЭДС самоиндукции, которая препятствует изменению тока. Величина индуктивного сопротивления зависит от индуктивности элемента и частоты протекающего тока:
Ёмкостное сопротивление (XC). Величина ёмкостного сопротивления зависит от ёмкости элемента С и также частоты протекающего тока:
См. также
Полезное
Смотреть что такое «Ёмкостное сопротивление» в других словарях:
ёмкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка). Ёмкостное сопротивление синусоидальному току Хс = 1/ωС, где ω угловая частота, С ёмкость. Измеряется в омах. * * * ЕМКОСТНОЕ… … Энциклопедический словарь
ёмкостное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN capacitancecondensancecapacitive reactancecapacity… … Справочник технического переводчика
ёмкостное сопротивление — talpinė varža statusas T sritis fizika atitikmenys: angl. capacitance; capacity reactance; capacitive reactance vok. kapazitiver Widerstand, m rus. ёмкостное сопротивление, n pranc. capacitance, f; réactance capacitive, f … Fizikos terminų žodynas
Ёмкостное сопротивление — см.Сопротивление ёмкостное … Большая советская энциклопедия
ЁМКОСТНОЕ СОПРОТИВЛЕНИЕ — см. Сопротивление ёмкостное … Большой энциклопедический политехнический словарь
ЁМКОСТНОЕ СОПРОТИВЛЕНИЕ — физ. величина, характеризующая сопротивление, оказываемое переменному току электрич. ёмкостью цепи (или её участка). Ё.с. синусоидальному току Хс = 1/w С, где w угловая частота, С ёмкость. Измеряется в омах … Естествознание. Энциклопедический словарь
зарядное ёмкостное сопротивление — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999 г.] Тематики электротехника, основные понятия EN charge capacitance … Справочник технического переводчика
СОПРОТИВЛЕНИЕ — (1) аэродинамическое (лобовое) сила, с которой газ действует на движущееся в нём тело. Оно всегда направлено в сторону, противоположную скорости движения тела, и является одной из составляющих аэродинамической силы; (2) С. гидравлическое… … Большая политехническая энциклопедия
ёмкостное реактивное сопротивление — — [http://slovarionline.ru/anglo russkiy slovar neftegazovoy promyishlennosti/] Тематики нефтегазовая промышленность EN capacitive reactance … Справочник технического переводчика
Сопротивление реактивное — электрическое, величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью (См. Электрическая ёмкость) и Индуктивностью цепи (её участка); измеряется в омах (См. Омаха). В случае синусоидального тока при… … Большая советская энциклопедия
Емкостное сопротивление.
Емкостное сопротивление в цепи переменного тока — это та часть сопротивления, которая создается конденсатором, включенным в цепь переменного тока (при пренебрежимо малой емкости подводящих проводов).
Для получения формулы емкостного сопротивления определим, как меняется сила тока в цепи, содержащей только конденсатор.

Напряжение на обкладках конденсатора u = φ1 – φ2 = q/C равно напряжению на входе цепи, поэтому
Для силы тока, которая определяется как производная заряда q по времени, из (q = C Um cos ωt) получим:
Между напряжением и силой тока в цепи с конденсатором наблюдается сдвиг фаз на π/2 (
Амплитуда силы тока равна
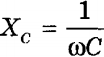
называется емкостным сопротивлением. Если вместо амплитуд силы тока и напряжения в (Im = Um Cω) использовать их действующие значения, то, учитывая 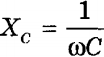
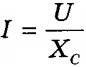
Это означает, что действующие значения силы тока и напряжения на конденсаторе связаны так же, как и сила постоянного тока и напряжение согласно закону Ома, причем роль активного сопротивления R играет емкостное сопротивление Хс.
Чем больше емкость конденсатора и частота напряжения, тем меньше емкостное сопротивление и тем больше ток перезарядки.
Благодаря сдвигу фаз между током и напряжением в среднем за период не происходит ни накопления энергии на конденсаторе, ни ее диссипации (рассеяния). За четверть периода, когда конденсатор заряжается до максимального значения, на нем происходит накопление энергии электрического поля; в следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Формула расчёта сопротивления конденсатора
Емкостное сопротивление конденсатора – величина, измеряемая в омах, создается непосредственно самим конденсатором, который включен в любую цепь. Оно должно иметь большую величину, то есть быть большим. Если на них происходит подача переменного тока, в устройстве происходят процессы заряда и последующего разряда. Последнее происходит по требованию цепи. При включении электрического тока, напряжение будет равно 0. Само устройство при этом начнет заряжаться, следовательно его величина напряжения постепенно растет. В случае необходимости, при достижении максимального заряда, произойдет разряд конденсатора.
В статье, посвященной теме расчета сопротивления конденсатора, приведена вся информация о процессе, как происходит заряд-разряд. В качестве бонуса есть интересный материал по теме, который можно скачать, и видеоролик в конце статьи.
Формула сопротивления
Формула ёмкостного сопротивления выводится следующим образом:
Чтобы получить значение ёмкостного сопротивления в омах, следует разделить единицу на число, полученное после умножения угловой частоты на ёмкость. Из этой формулы вытекает, что чем больше ёмкость конденсатора или частота переменного тока, тем меньше его сопротивление. Когда частота будет равна нулю (постоянный ток), ёмкостное сопротивление станет бесконечно большим. Конденсатор очень большой ёмкости будет проводить ток в широком диапазоне частот.
Применение на практике
Свойства конденсатора используются при конструировании различных фильтров. Действие ёмкостного сопротивления в этом случае зависит от способа подключения детали:
В фильтрах электропитания, наряду с ёмкостным сопротивлением, используется также свойство накопления и отдачи заряда. В момент повышения нагрузки заряженная ёмкость фильтра разряжается, отдавая дополнительную энергию. Она также осуществляет подавление пульсаций и прочих паразитных сигналов, пропуская их через себя и замыкая на общий провод. Таким образом, обеспечивается сглаживание и поддержание напряжения на нагрузке в заданных пределах, и устранение нежелательных междукаскадных связей, вызывающих нестабильную работу.
Характеристики прибора
Важнейшей характеристикой накопительного прибора является ёмкость. От неё зависит время заряда при подключении устройства к источнику тока. Время разряда напрямую связано со значением сопротивления нагрузки: чем оно выше, тем быстрее происходит процесс отдачи накопленной энергии. Определяется эта ёмкость следующим выражением:
C = E*Eo*S / d, где E — относительная диэлектрическая проницаемость среды (справочная величина), S — площадь пластин, d — расстояние между ними. Кроме ёмкости конденсатор характеризуется рядом параметров, такими как:
Импеданс элемента
Общее сопротивление конденсатора (импеданс) переменному сигналу складывается из трёх составляющих: ёмкостного, резистивного и индуктивного сопротивления. Все эти величины при конструировании схем, содержащих накопительный элемент, необходимо учитывать. В ином случае в электрической цепи, при соответствующей обвязке, конденсатор может вести себя как дроссель и находится в резонансе.
Последняя возникает из-за появления электродвижущей силы (ЭДС) самоиндукции. Непостоянство тока приводит к изменению магнитного потока, поддерживающего ток ЭДС самоиндукции постоянным. Это значение определяется индуктивностью L и частотой протекающих зарядов W. Xl = wL = 2*p*f*L. Xc — ёмкостное сопротивление, зависящее от ёмкости накопителя C и частоты тока f. Xc = 1/wC = ½*p*f*C, где w — круговая частота.
Разница между ёмкостным и индуктивным значениями называется реактивным сопротивлением конденсатора: X = Xl-Xc. По формулам можно увидеть, что при увеличении частоты f сигнала начинает преобладать индуктивное значение, при уменьшении — ёмкостное. Поэтому если:
Активное сопротивление R связывается с потерями мощности, превращением её электрической энергии в тепловую. Реактивное – с обменом энергии между переменным током и электромагнитным полем. Таким образом, полное сопротивление можно найти, используя формулу Z = R +j*X, где j — мнимая единица.
Пример расчёта
Практическое применение формул можно рассмотреть при решении задачи. Пусть имеется RC цепочка, состоящая из ёмкости C = 1 мкФ и сопротивления R = 5 кОм. Необходимо найти импеданс этого участка и ток цепи, если частота сигнала равна f = 50 Гц, а амплитуда U = 50 В.
В первую очередь понадобится определить сопротивление конденсатора в цепи переменного тока для заданной частоты. Подставив данные в формулу, получим, что для частоты 50 Гц сопротивление будет
Xc = 1/ (2*p*F*C) = 1/ (2*3,14*50*1* 10 −6 ) = 3,2 кОм.
По закону Ома можно найти ток: I = U /Xc = 50 /3200 = 15,7 мА.
Напряжение берётся изменяемым по закону синуса, поэтому: U (t) = U * sin (2*p*f*t) = 50*sin (314*t). Соответственно, ток будет I (t) = 15,7* 10 −3 + sin (314*t+p/2). Используя полученные результаты, можно построить график тока и напряжения при этой частоте. Общее сопротивление участка цепи находим как Z = (5000 2 +3200 2 )½ = 5 936 Ом =5,9 кОм.
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C. RC цепь Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU.
Здесь U – напряжение источника питания. Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Резистор обладает активным (омическим) сопротивлением. Катушка индуктивности и конденсатор обладают реактивным сопротивлением. В цепи переменного тока на конденсаторе ток опережает напряжение на 90 градусов, а на катушке ток отстает от напряжения на 90 градусов. Сопротивление катушки вычисляется по формуле. Сопротивление конденсатора вычисляется по формуле:
В цепи переменного тока на идеальном реактивном сопротивлении не выделяется мощность.
Заключение
В данной статье были рассмотрены основные вопросы расчета сопротивления конденсаторов. Больше информации можно найти в скачиваемой версии учебника по электромеханике “Что такое конденсаторы”
Емкостное сопротивление
Использование ёмкости в цепи постоянного тока знакомо каждому электронщику. В этом случае работа детали описывается сравнительно простыми физическими законами. Несколько сложнее дела обстоят с переменным током, ведь при таком применении ёмкости уже возникает необходимость учитывать реактивное сопротивление.
Формула ёмкостного сопротивления
При подаче на обкладки конденсатора переменного напряжения ток через этот элемент первоначально стремится к максимальному значению. По мере заряда прибора он постепенно снижается. В то же время вольтаж ведёт себя иначе, т.е. плавно возрастает от нуля до максимального значения.
Подобный эффект вызван ёмкостным сопротивлением. Оно зависит как от строения самого электронного прибора, так и от характеристик поданного на него переменного напряжения.
Обратите внимание! Ёмкость элемента можно узнать по маркировке, имеющейся на его корпусе. Если она нечитаемая или стёрлась, то эта величина определяется с помощью мультиметра. Он должен быть с функцией замера ёмкости (прим. DT9208A).
Векторное представление ёмкости
Для простоты понимания процессов, происходящих в конденсаторе под действием источника переменного тока, удобно воспользоваться векторным представлением ёмкости.
В начальный момент зарядки конденсатора потенциал U на его обкладках равен нулю (точка a). В то же время ток I имеет своё максимальное значение (точка b). На этом этапе уже заметно отставание. Ток начинает снижаться со своей пиковой величины (участок bd). Напряжение в этот момент ещё не выросло и только подбирается к своему максимуму (ac).
Подобное отражается и на диаграмме справа. В момент, когда вольтаж U имеет своё наименьшее значение (e), ток I только начинает переходить в отрицательную область (f).
Емкостное сопротивление
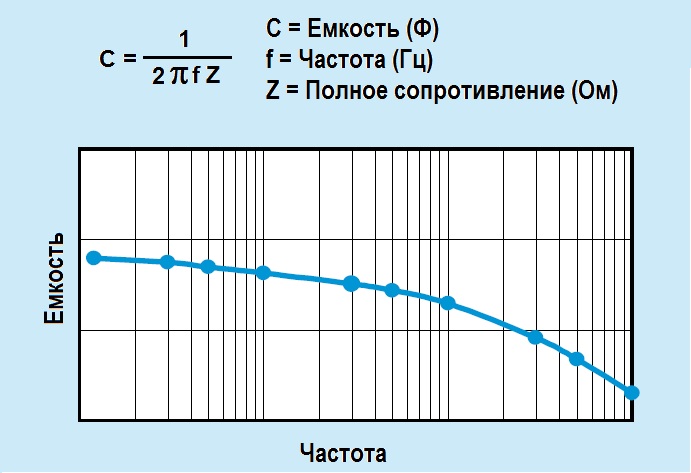
Ёмкостное, оно же реактивное, сопротивление принципиально зависит от частоты напряжения. Данная связь хорошо видна на графике, приведённом ниже. Чем выше частота, тем меньше реактивное сопротивление. Очевидно это и из вышеприведённой формулы. Переменная f (частота) стоит в знаменателе. Поэтому с её увеличением Xc будет уменьшаться.
Емкость в цепи переменного тока
При подаче на конденсатор постоянного напряжения он постепенно зарядится до максимальной разности потенциалов на его обкладках. После этого ток через электронный компонент прекратится и, не считая ничтожной утечки, будет равняться нулю. Поэтому в цепи постоянного тока конденсатор имеет огромное сопротивление. При расчетах его величину принимают равной бесконечности.
Реактивное сопротивление имеет вполне исчисляемое значение. Его можно измерить с помощью осциллографа, генератора и постоянного резистора. Для этого потребуется собрать схему. В ней конденсатор образует с резистором делитель напряжения. С помощью осциллографа будет измеряться потенциал, который образуется на выводах ёмкости.
Для данной схемы вычисления имеют следующий вид.
Здесь:
Важно! Электрический кабель также обладает ёмкостью. Поэтому после снятия напряжения на нём остаётся некоторый заряд. Данное явление опасно для человека, особенно, если проводник до отключения находился под потенциалом 1000 В и выше.
Единицы измерения
Для правильного проведения всех расчетов важно понимать, какие величины в них используются, и что они обозначают:
Пример расчета емкостного сопротивления
Для расчета понадобится большинство из перечисленных физических величин. Они обозначены на схеме и в качестве примера имеют следующие значения:
Реактив будет рассчитываться по вышеописанной формуле:
В таком случае сопротивление конденсатора в цепи переменного тока равно 96,5 кОм. Если расписать все вычисления, то получится следующее.
Сама по себе формула не вызывает сложности. Однако для проведения вычислений необходимы знания школьного курса алгебры, т.е. умение работать со степенями, дробями и прочими алгоритмами математики. На практике имеет смысл немного схитрить. Чтобы каждый раз не городить сложные вычисления, можно воспользоваться одним из онлайн калькуляторов из сети Интернет. Подобные ресурсы позволяют произвести комплексный расчёт и выяснить некоторые другие параметры цепи.
Свойства ёмкостей
Основное свойство состоит в их способности накапливать и отдавать электрический заряд. Оба этих процесса происходят не мгновенно, а за вполне определённый период, который поддаётся расчету. Данное свойство используется для создания различных времязадающих RC цепей. Если зарядить конденсатор до некоторого значения, то время его разряда через резистор R будет зависеть от ёмкости C.
Ещё одно распространённое свойство конденсаторов – это возможность ограничивать переменный ток. Вызвана она реактивом этих элементов. Ёмкость, включенная в цепь переменного тока, ограничивает его до значения I = 2pfCU. Здесь U – напряжение источника питания.
Дополнительная информация. Ёмкость, подключенная параллельно с катушкой, имеющей индуктивный характер сопротивления, называется колебательным контуром. Данная цепь обладает высокой амплитудой колебаний на резонансной частоте. Она применяется для выделения из множества окружающих радиосигналов именно того, на который требуется настроить приём.
Сопротивление – это одна их характеристик конденсатора, подключенного к цепи переменного тока. Понимание процессов, происходящих с этим элементом в подобных схемах, существенно расширяет сферу его использования. Реактивное сопротивление конденсаторов учитывается как в простых бытовых электроприборах, так и в сложной вычислительной технике.
Видео
Особенности расчета емкостного сопротивления
Электросопротивление — это параметр в электротехнике, характеризующий возможность вещества препятствовать прохождению электричества. В зависимости от качеств материала, электросопротивляемость может уменьшаться до крайне маленьких величин (микро\милиОмы — у проводников, металлов) или повышаться до огромных значений (ГигаОмы — изоляторов, диэлектриков). Величина противоположная сопротивлению — проводимость.
Что такое
Цепь, по которой протекает непостоянный ток, обладает полным сопротивлением. Вычисляется оно по сумме активного и реактивного сопротивлений, возведенных в квадрат.

Графическое изображение этой формулы представляет собой треугольник. Его катеты представлены активным и реактивным сопротивлениями, а гипотенуза полным электросопротивлением.

Емкостное электросопротивление (Xc) является одним из видов реактивного сопротивления. Этот показатель характеризует противодействие электроемкости в цепи электротоку с переменными параметрами. Преобразование электроэнергии в тепловую в момент протекания электричества сквозь емкость не возникает (свойство реактивного сопротивления). Вместо этого осуществляется передача энергии электрического тока электрическому полю и обратно. Потерь энергии при таком обмене не происходит.
Емкостное сопротивление конденсатора можно сравнить с кастрюлей, наполняемой жидкостью, при полном заполнении ее объема она переворачивается, выливая содержимое, а затем наполняется заново. После достижения максимального заряда конденсатора происходит разрядка, затем он заряжается вновь.
Дополнительная информация: Конденсатор цепи способен накопить лишь ограниченную величину заряда до перемены полярности напряжения. По данной причине непостоянный ток не падает до нуля, важное отличие от постоянного электричества. Низкие значения частоты тока соответствуют низким показателям заряда, накопленного конденсатором, низким значениям противодействия электричеству, что придает реактивные свойства.
По сути, Xc — это противостояние электродвижущей силы конденсатора, уровню его заряда.
От чего зависит сопротивление конденсаторов цепей переменного тока
Показатели его, зависят не только от емкостных характеристик последнего, но и от частотной характеристики электротока, протекающего по цепи. Когда речь идет о сопротивлении резистора, то говорится о параметрах самого резистора, например, материале, форме, но полностью отсутствует взаимосвязь сопротивления его и показателей частоты электричества цепи (речь идет об идеальном резисторе, паразитные параметры которому не характерны). Когда речь идет об устройстве накопления энергии и заряда электрического поля — все иначе. Конденсатор одной и той же емкости при разных частотах тока обладает неодинаковым уровнем сопротивления. Амплитуда протекающего через него электричества при постоянной амплитуде напряжения обладает разной величиной.
Рассматривая эту формулу сопротивления конденсатора в цепи переменного тока, к каким выводам можно прийти? При повышении частотных показателей сигнала, электросопротивляемость конденсатора снижается.
При повышении емкостных характеристик устройства для накопления заряда и энергии электрического поля Xc переменного электричества, проходящего сквозь него, будет стремиться вниз.

Момент приближения значений частоты к нулевым отметкам на оси (когда переменный электроток становится похож своими параметрами на постоянный), сопровождается возрастанием Xc конденсатора до беспредельных величин. Это действительно так: известно, что конденсатор сети постоянного тока является фактически разрывом цепи. Реальная электросопротивляемость, естественно, не бесконечна, ее ограничивает уровень конденсаторной утечки. Но величины его остаются на высоком уровне, который невозможно не учитывать.
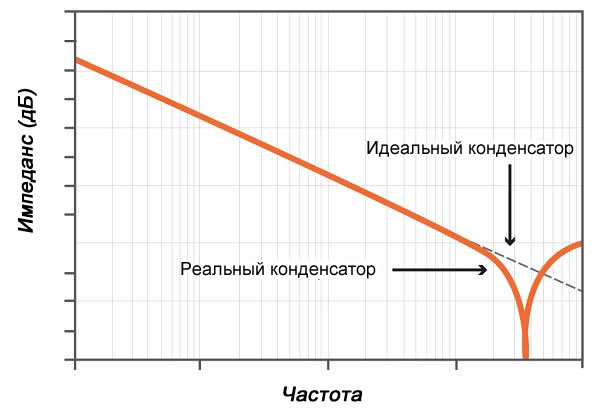
При возрастании цифр частоты до уровня бесконечных значений, емкостное сопротивление электроконденсатора стремится к нулевым отметкам. Такое характеризует идеальные модели. В реальных условиях конденсатор имеет неприятные характеристики (такие как индуктивность и сопротивления утечек), поэтому снижение емкостного сопротивления происходит до определенных значений, после которых оно возрастает.
Обратите внимание! При подключении конденсатора к цепочке электричества с переменными параметрами, его мощность не тратится, потому что фазовые характеристики напряжения и силы тока сдвинуты на 90° в отношении друг друга. В одну четверть периода происходит зарядка электроконденсатора (энергия запасается в его электрополе), в следующее время происходит его разрядка, энергия поступает обратно в цепочку. Его электросопротивляемость является безваттной, реактивной.
Причины ёмкостного сопротивления
Причиной возникновения сопротивления емкостного считается уровень напряжения, возникающий на конденсаторе в процессе его заряда. Вектор его действия встречен вектору напряжения источника электричества, потому создает помеху воспроизведению электротока этим источником.
Как рассчитать Xc


Получается, что изменения напряжения отличаются по фазе от изменений тока на π/2.
По закону, сформулированному Омом, показатели силы электротока находятся в прямой пропорциональной зависимости от величины напряжения цепи. Формула вычисления наибольших величин напряженности и силы тока:
f — показатель частоты непостоянного тока, измеряется в герцах;
ω — показатель угловой частоты тока;
С — размер конденсатора в фарадах.
Важно! Xc не выступает параметром проводника, оно находится в зависимости от такой характеристики электроцепи, как частота электротока.
Повышение значений данной величины вызывает рост пропускающей способности конденсатора (предел его сопротивления току непостоянному понижается).
Представим, к цепи подключен конденсатор, емкостью 1 мкФ. Необходимо вычислить, уровень емкостного сопротивления при величине частоты 50 Гц и как изменится емкостное сопротивление цепи переменного тока при частоте 1 кГц. Амплитуда напряжения, подведенного к конденсатору, составляет 50 В.
После введения данных в формулу, определяющую Xc, и получаются значения:


Емкостное сопротивление приравнивается к соотношению отклонений колебаний напряжения зажимов электрической цепочки с емкостными параметрами (с небольшими индуктивным и активным сопротивлениями) к колебаниям электротока цепочки. Она равнозначна электроконденсатору.
В чем измеряется емкостное электросопротивление
R представлено отношением напряжения к силе тока замкнутой электрической цепи, по закону Ома. Единицы измерения — Ом. Xc, как его разновидность, тоже измеряется в Омах.
Конденсаторы применяются при изготовлении фильтров. При параллельном присоединении к цепи, он способен задерживать высокие частоты, при последовательном удаляет низкие. Также они используются с целью отсечения переменной части от постоянной. Он незаменим в радиотехнике, при производстве датчиков приближения, для контроля процессов производства. Технологии, обладающие выше описанными свойствами, используются во всех областях промышленности.