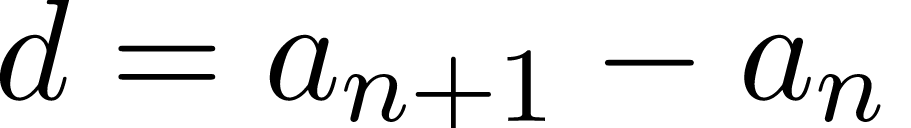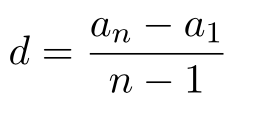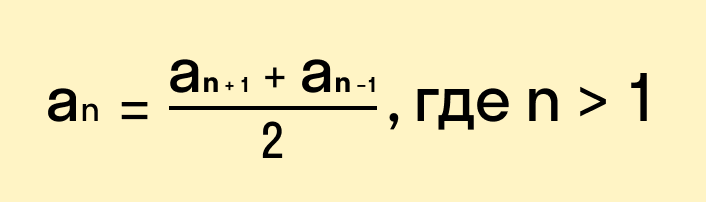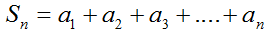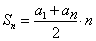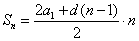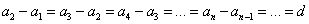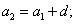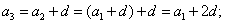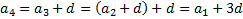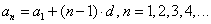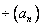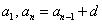какую последовательность называют арифметической прогрессией

a_n+1= a_n + d, где d — это разность арифметической прогрессии.

Описать словами эту формулу можно так: каждый член арифметической прогрессии равен предыдущему, сложенному с одним и тем же числом d.

Разность между последующим и предыдущим членами, то есть разность арифметической прогрессии можно найти по формуле:

Если известны первый член a₁ и n-ый член прогрессии, разность можно найти так:

Арифметическая прогрессия бывает трех видов:

Пример: последовательность чисел 11, 14, 17, 20, 23. — это возрастающая арифметическая прогрессия, так как ее разность d = 3 > 0.

Свойство арифметической прогрессии

Переведем с языка формул на русский: каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому двух соседних с ним членов. Что как раз объясняет название «арифметическая» прогрессия.

Рассмотрим пример арифметической прогрессии.

Дано: арифметическая прогрессия (a_n), где a₁ = 0 и d = 2.

Найти: первые пять членов прогрессии и десятый член прогрессии.

Решение арифметической прогрессии:

По условиям задачи n = 10, подставляем в формулу:

Формулы арифметической прогрессии

В 9 классе проходят все формулы арифметической прогрессии. Давайте узнаем, какими способами ее можно задать:

Сумма первых n членов арифметической прогрессии (а_n) обозначается S_n:

Формулы нахождения суммы n членов арифметической прогрессии:

Чтобы быстрее запомнить формулы можно использовать такую табличку с основными определениями:

Формула n-го члена арифметической прогрессии

Из определения арифметической прогрессии следует, что равенство истинно:

Значит,

Переведем с языка формул на русский: если мы знаем первый член и разность арифметической прогрессии, то можем найти любой ее член.

Арифметическую прогрессию можно назвать заданной, если известен ее первый член и разность.

Доказательство формулы n-го члена арифметической прогрессии

Формулу n-го члена арифметической прогрессии можно доказать при помощи метода математической индукции.

Пусть дано:

Нужно доказать:

Действительно,

Согласно принципу математической индукции формула верна для любого натурального числа.

Геометрическая прогрессия

Геометрическая прогрессия — это последовательность (b_n), в которой каждый последующий член можно найти, если предыдущий член умножить на одно и то же число q.

Если последовательность (b_n) является геометрической прогрессией, то для любого натурального значения n справедлива зависимость:

Если в геометрической прогрессии (b_n) известен первый член b₁ и знаменатель q, то можно найти любой член прогрессии:

Общий член геометрической прогрессии bn можно вычислить при помощи формулы:

Пример 1. 2, 6, 18, 54,… — геометрическая прогрессия b = 2, q = 3.

Пример 3. 7, 7, 7, 7,… — геометрическая прогрессия b = 7, q = 1.

Источник

Арифметическая прогрессия (ЕГЭ 2022)

Знаменитый ученый Карл Гаусс однажды сказал:

«Ничего не сделано, если что-то осталось недоделанным.»

Поэтому давай сейчас разберем одну из важнейших тем алгебры – арифметическую прогрессию.

А если остались какие-то пробелы, заполним их.

Кстати, Гаусса мы вспомнили не просто так 🙂

Арифметическая прогрессия — коротко о главном

Определение арифметической прогрессии:

Арифметическая прогрессия — это числовая последовательность, в которой разница между соседними числами одинакова и равна \( \displaystyle d\).

Арифметическая прогрессия бывает возрастающей (\( \displaystyle d>0\)) и убывающей (\( \displaystyle d Формула нахождения n-ого члена арифметической прогрессии:

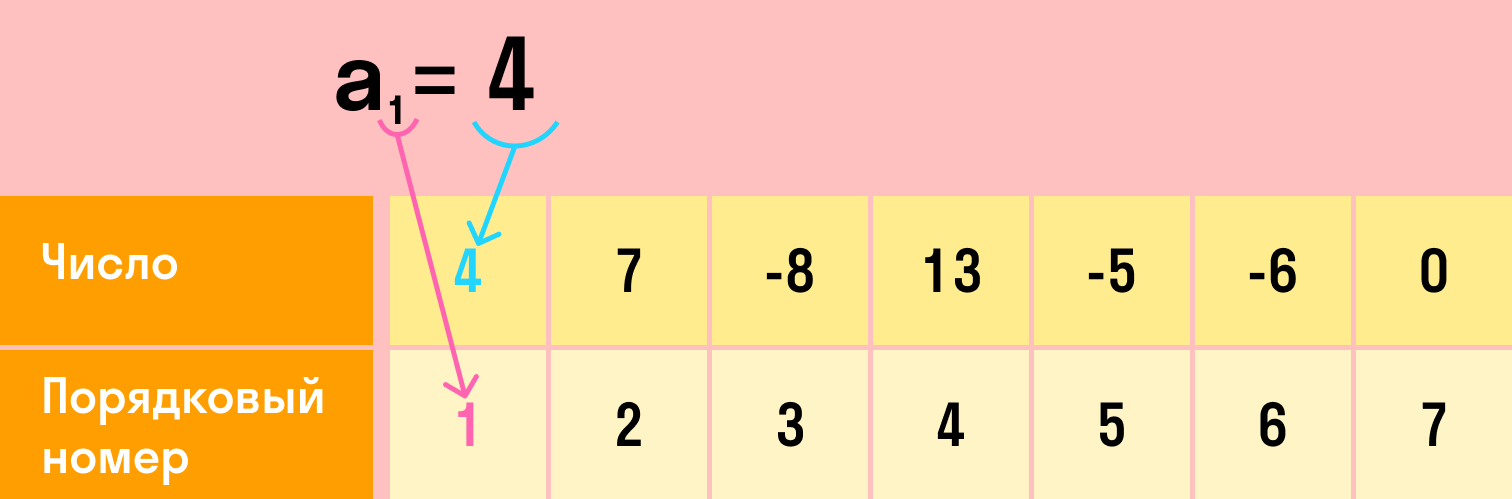
Как найти член прогрессии, если известны его соседние члены:

Сумма членов арифметической прогрессии:

Числовая последовательность

Итак, сядем и начнем писать какие-нибудь числа. Например: \( \displaystyle 4,\text< >7,\text< >-8,\text< >13,\text< >-5,\text< >-6,\text< >0,\text< >\ldots \)

Писать можно любые числа, и их может быть сколько угодно (в нашем случае их \( \displaystyle 7\)). Сколько бы чисел мы не написали, мы всегда можем сказать, какое из них первое, какое – второе и так далее до последнего, то есть, можем их пронумеровать.

Это и есть пример числовой последовательности.

Числовая последовательность – это множество чисел, каждому из которых можно присвоить уникальный номер.

Например, для нашей последовательности:

Присвоенный номер характерен только для одного числа последовательности. Иными словами, в последовательности нет трех вторых чисел. Второе число (как и \( \displaystyle n\)-ное число) всегда одно.

Число с номером \( \displaystyle n\) называется \( \displaystyle n\)-ным членом последовательности.

Всю последовательность мы обычно называем какой-нибудь буквой (например, \( \displaystyle a\)), и каждый член этой последовательности – той же буквой с индексом, равным номеру этого члена: \( \displaystyle <_<1>>,\text< ><_<2>>,\text< >…,\text< ><_<10>>,\text< >…,\text< ><_>\).

Арифметическая прогрессия — определения

Допустим, у нас есть числовая последовательность, в которой разница между соседствующими числами одинакова и равна d.

Такая числовая последовательность называется арифметической прогрессией.

Термин «прогрессия» был введен римским автором Боэцием еще в 6 веке и понимался в более широком смысле, как бесконечная числовая последовательность.

Название «арифметическая» было перенесено из теории непрерывных пропорций, которыми занимались древние греки.

Арифметическая прогрессия – это числовая последовательность, каждый член которой равен предыдущему, сложенному с одним и тем же числом. Это число называется разностью арифметической прогрессии и обозначается d.

Попробуй определить, какие числовые последовательности являются арифметической прогрессией, а какие нет:

Разобрался? Сравним наши ответы:

Является арифметической прогрессией – 2, 3.

Не является арифметической прогрессией – 1, 4.

Вернемся к заданной прогрессии (\( \displaystyle 3;\text< >7;\text< >11;\text< >15;\text< >19\ldots \)) и попробуем найти значение ее 6-го члена.

Существует два способа его нахождения.

Нахождения n-ого члена арифметической прогрессии

Способ I

Итак, 6-ой член описанной арифметической прогрессии равен 23.

Способ II

А что если нам нужно было бы найти значение \( \displaystyle 140\)-го члена прогрессии? Суммирование заняло бы у нас не один час, и не факт, что мы не ошиблись бы при сложении чисел.

А теперь очень важно! Чтобы облегчить себе работу, нужно найти закономерность, потом описать ее формулой и потом пользоваться этой формулой, чтобы вычислять в разы быстрее.

Это и есть математика!

Важно научиться находить закономерности, а потом уже запоминать формулы. Потому что, даже если ты забудешь формулу, ты сможешь ее вывести. И, самое главное, ты сможешь проверить подходит та или иная формула для решения задачи, а не просто подставлять их как обезьянка.

Давай попробуем вывести формулу. Это легко и тебе понравится! Чтобы найти закономерности, надо пользоваться тем, что мы знаем.

Чему равен 2-й член арифметической прогрессии? Попробуй сначала написать числами, а потом в более общем виде, заменив числа буквами.

Закономерности пока не видны. Ок. Идем дальше. Чему равен 3-й член арифметической прогрессии?

Похоже что вырисовывается закономерность! Чтобы узнать значение 2-го члена прогрессии, мы прибавляли одно d, а чтобы узнать 3-го — два d! Иными словами, нам надо прибавлять каждый раз на одно d меньше, чем номер члена прогрессии.

Давай проверим? Чему равен 4-й член арифметической прогрессии?

Бинго! Закономерность подтверждается. Теперь осталось описать закономерность формулой и пользоваться ею!

Если нам нужно найти значение числа прогрессии с порядковым номером n, мы прибавляем к первому члену арифметической прогрессии число d, которое на одно значение меньше порядкового номера искомого числа.

А теперь запомни эту формулу и используй ее для быстрого счета. А если забудешь — то легко выведешь.

Например, посмотрим, из чего складывается значение \( \displaystyle 4\)-го члена данной арифметической прогрессии:

Попробуй самостоятельно найти таким способом значение члена \( \displaystyle n=6\) данной арифметической прогрессии.

Рассчитал? Сравни свои записи с ответом:

Обрати внимание, что у тебя получилось точно такое же число, как и в предыдущем способе, когда мы последовательно прибавляли \( \displaystyle d\) к предыдущему значению членов арифметической прогрессии.

Попробуем «обезличить» данную формулу – приведем ее в общий вид и получим:

Кстати, таким образом мы можем посчитать и \( \displaystyle 140\)-ой член данной арифметической прогрессии (да и \( \displaystyle 169\)-ый тоже можем, да и любой другой вычислить совсем несложно).

Попробуй посчитать значения \( \displaystyle 140\)-го и \( \displaystyle 169\)-го членов, применив полученную формулу.

Возрастающие и убывающие арифметические прогрессии

Возрастающие – прогрессии, в которых каждое последующее значение членов больше предыдущего.

Убывающие – прогрессии, в которых каждое последующее значение членов меньше предыдущего.

Выведенная формула применяется в расчете членов как в возрастающих, так и в убывающих членах арифметической прогрессии.

Проверим это на практике.

Нам дана арифметическая прогрессия, состоящая из следующих чисел: \( \displaystyle 13;\text< >8;\text< >4;\text< >0;\text< >-4.\)

Проверим, какое получится \( \displaystyle 4\)-ое число данной арифметической прогрессии, если при его расчете использовать нашу формулу:

Заметим, что так как арифметическая прогрессия убывающая, то значение \( \displaystyle d\) будет отрицательным, ведь каждый последующий член меньше предыдущего.

Таким образом, мы убедились, что формула действует как в убывающей, так и в возрастающей арифметической прогрессии.

Попробуй самостоятельно найти \( \displaystyle 140\)-ой и \( \displaystyle 169\)-ый члены этой арифметической прогрессии.

Сравним полученные результаты:

Свойство арифметической прогрессии (или как найти n-й член прогрессии, зная соседние)

Усложним задачу — выведем свойство арифметической прогрессии.

Допустим, нам дано такое условие:

\( \displaystyle 4;\text< >x;\text< >12\ldots \) — арифметическая прогрессия, найти значение \( \displaystyle x\).

Легко, скажешь ты и начнешь считать по уже известной тебе формуле:

Получается, мы сначала находим \( \displaystyle d\), потом прибавляем его к первому числу и получаем искомое \( \displaystyle x\).

Если прогрессия представлена маленькими значениями, то ничего сложного в этом нет, а если нам в условии даны числа \( \displaystyle 4024;

Согласись, есть вероятность ошибиться в вычислениях.

А теперь подумай, можно ли решить эту задачу в одно действие с использованием какой-либо формулы?

Конечно да, и именно ее мы попробуем сейчас вывести.

Просуммируем предыдущий и последующий члены прогрессии:

Получается, что сумма предыдущего и последующего членов прогрессии – это удвоенное значение члена прогрессии, находящегося между ними.

Иными словами, чтобы найти значение члена прогрессии при известных предыдущих и последовательных значениях, необходимо сложить их и разделить на \( 2\).

Попробуем посчитать значение \( x\), используя выведенную формулу:

Все верно, мы получили это же число. Закрепим материал.

Посчитай значение \( x\) для прогрессии \( \displaystyle 4024;

x;6072\) самостоятельно, ведь это совсем несложно.

Молодец! Ты знаешь о прогрессии почти все!

Осталось узнать только одну формулу, которую по легендам без труда вывел для себя один из величайших математиков всех времен, «король математиков» – Карл Гаусс…

Сумма первых n членов арифметической прогрессии

Когда Карлу Гауссу было 9 лет, учитель, занятый проверкой работ учеников других классов, задал на уроке следующую задачу:

«Сосчитать сумму всех натуральных чисел от \( \displaystyle 1\) до \( \displaystyle 40\) (по другим источникам до \( \displaystyle 100\)) включительно».

Каково же было удивление учителя, когда один из его учеников (это и был Карл Гаусс) через минуту дал правильный ответ на поставленную задачу, при этом, большинство одноклассников смельчака после долгих подсчетов получили неправильный результат…

Юный Карл Гаусс заметил некоторую закономерность, которую без труда заметишь и ты.

Допустим, у нас есть арифметическая прогрессия, состоящая из \( \displaystyle 6\)-ти членов: \( \displaystyle 6;\text< >8;\text< >10;\text< >12;\text< >14;\text< >16…\)

Нам необходимо найти сумму данных \( \displaystyle 6\) членов арифметической прогрессии.

Конечно, мы можем вручную просуммировать все значения, но что делать, если в задании необходимо будет найти сумму \( \displaystyle 100\) ее членов, как это искал Гаусс?

Изобразим заданную нам прогрессию. Присмотрись внимательно к выделенным числам и попробуй произвести с ними различные математические действия.

Попробовал? Что ты заметил? Правильно! Их суммы равны

А теперь ответь, сколько всего наберется таких пар в заданной нам прогрессии?

Конечно, ровно половина всех чисел, то есть \( \frac<6><2>=3\).

Исходя из того, что сумма двух членов арифметической прогрессии равна \( 22\), а подобных равных пар \( 3\), мы получаем, что общая сумма равна:

\( \displaystyle S\text< >=\text< >22\cdot 3\text< >=\text< >66\).

Таким образом, формула для суммы первых \( \displaystyle n\) членов любой арифметической прогрессии будет такой:

В некоторых задачах нам неизвестен \( \displaystyle n\)-й член, но известна разность прогрессии. Попробуй подставить в формулу суммы, формулу \( \displaystyle n\)-го члена. \( <_>=<_<1>>+d\left( n-1 \right)\)

Что у тебя получилось?

Молодец! Теперь вернемся к задаче, которую задали Карлу Гауссу: посчитай самостоятельно, чему равна сумма \( \displaystyle 40\) чисел, начиная от \( \displaystyle 1\)-го, и сумма \( \displaystyle 100\) чисел начиная от \( \displaystyle 1\)-го.

Сколько у тебя получилось?

У Гаусса получилось, что сумма \( \displaystyle 100 \) членов равна \( \displaystyle 5050\), а сумма \( \displaystyle 40 \) членов \( \displaystyle 820\).

На самом деле формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом еще в 3 веке, да и на протяжении всего этого времени остроумные люди вовсю пользовались свойствами арифметической прогрессии.

Например, представь Древний Египет и самую масштабную стройку того времени – строительство пирамиды… На рисунке представлена одна ее сторона.

Где же здесь прогрессия скажешь ты? Посмотри внимательно и найди закономерность в количестве песчаных блоков в каждом ряде стены пирамиды.

Чем не арифметическая прогрессия? Посчитай, сколько всего блоков необходимо для строительства одной стены, если в основание кладется \( \displaystyle 6\) блочных кирпичей.

Надеюсь, ты не будешь считать, водя пальцем по монитору, ты же помнишь последнюю формулу и все, что мы говорили об арифметической прогрессии?

В данном случае прогрессия выглядит следующим образом:

\( \displaystyle 6;\text< >5;\text< >4;\text< >3;\text< >2;\ 1\).

Разность арифметической прогрессии \( \displaystyle

Количество членов арифметической прогрессии \( \displaystyle=6\).

Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Разность арифметической прогрессии \( \displaystyle

Количество членов арифметической прогрессии \( \displaystyle=6\).

Подставим в последние формулы наши данные (посчитаем количество блоков 2 способами).

Способ 1.

Способ 2.

А теперь можно и на мониторе посчитать: сравни полученные значения с тем количеством блоков, которое есть в нашей пирамиде.

Молодец, ты освоил сумму \( \displaystyle n\)-ных членов арифметической прогрессии.

Конечно, из \( \displaystyle 6\) блоков в основании пирамиду не построишь, а вот из \( \displaystyle 60\)?

Попробуй рассчитать, сколько необходимо песчаных кирпичей, чтобы построить стену с таким условием.

Верный ответ – \( \displaystyle 1830\) блоков:

Источник

Арифметическая прогрессия и сумма ее членов

теория по математике 📈 последовательности

Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.

Другими словами, последовательность (а_n) – арифметическая прогрессия, если для любого натурального числа n выполняется условие а_n+1=а_n+d, где d – некоторое число. Из данного равенства следует, что можно найти это число d, если вычесть из последующего члена предыдущий, то есть d = а_n+1–а_n. Число d называют разностью арифметической прогрессии.

Арифметической прогрессией, например, является ряд чисел 3; 8; 13; 18…. так как разница между числами равна 5, мы видим, что каждое последующее на 5 больше предыдущего.

Если известен первый член арифметической прогрессии a₁ и разность d, то можно вычислить любой член арифметической прогрессии:

Этот ряд можно продолжать до бесконечности, поэтому надо запомнить, что n-ый член арифметической прогрессии можем получить быстрее, если к первому члену прогрессии добавить (n−1) разностей, то есть:

Формула n-ого члена арифметической прогрессии

где n – порядковый номер члена арифметической прогрессии, a₁ – первый член прогрессии, d – разность арифметической прогрессии

Формулу используют, чтобы вычислить заданный член арифметической прогрессии (например, пятнадцатый, двухсотый и т.д.), если известны первый член последовательности и ее разность. Рассмотрим на примерах применение данной формулы.

Пример №1. Найти а₂₀ арифметической прогрессии (а_n), если а₁=14, d=5. Составляем формулу для а₂₀ и подставляем в нее данные: а₂₀= a₁ + d(20−1)=14+5(20−1)=109. Таким образом, мы вычислили, что на 20-ом месте в данной арифметической прогрессии стоит число 109.

Найти а₇ арифметической прогрессии (а_n), если а₁=−8, d=−3. Аналогично работаем, составляя формулу и подставляя в нее данные значения (обращаем внимание на знаки чисел, чтобы не допустить ошибок): а₇= a₁ + d(7−1)= −8−3(7−1)= −26.

Дана арифметическая прогрессия 10; 12; 14;…… Найти а_12. Здесь для нахождения а₁₂ надо сначала найти разность d: d=12−10=2, то есть из последующего вычтем предыдущее. Можно было 14−12, порядок здесь не имеет значения, главное берем два соседних члена прогрессии. Теперь можем составлять формулу и находить а₁₂: а₁₂= a₁ + d(12−1)=10+2(12−1)=32.

Любая арифметическая прогрессия может быть задана формулой вида a_n=kn+b, где k и b некоторые числа. Верно и обратное утверждение: если последовательность чисел задана формулой вида a_n=kn+b, где k и b некоторые числа, то она является арифметической.

Так, например, формула a_n=5n+1 задает арифметическую прогрессию, в которой разность d равна 1; по данной формуле можно найти любой член последовательности, например, найдем 20-ый член, подставляя в формулу число 20: a₂₀=5 × 20+1=101.

Свойство арифметической прогрессии

Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов. Формула:

Другими словами, используя данное свойство, мы можем найти член арифметической прогрессии, стоящий между двумя известными членами, без использования разности d. Рассмотрим это на примерах.

Пример №2. Найти а₁₀ арифметической прогрессии (а_n), если а₉=24; а₁₁=38. Здесь используем свойство, так как видим, что у а₁₀ известны соседние члены. Значит, а₁₀=(а₉+а₁₁):2=(24+38):2=31. Таким образом, десятый член равен 31.

Дана арифметическая прогрессия …..23; х; 35. Найти х. Применяем свойство для нахождения х: х=(23+35):2=29. Для наглядности запишем, что ряд чисел выглядит так: …23; 29; 35.

Формулы суммы n первых членов арифметической прогрессии

В данной формуле мы видим, что для нахождения суммы нужны первый и последний член прогрессии. Но встречаются случаи, когда а_n не известно, но известна разность. Тогда для нахождения суммы применяют вторую формулу.

Формула суммы членов арифметической прогрессии с первым членом и разностью

Рассмотрим на примерах применение данных формул.

Пример №3. Найти сумму первых пятидесяти членов арифметической прогрессии (а_n), если а₁=11, а₅₀=39.

Для решения лучше использовать первую формулу, так как здесь есть первый и последний члены: а₁=11, а₅₀=39. Поэтому составляем формулу, подставляем в нее данные значения и вычисляем:

Найти сумму первых десяти членов арифметической последовательности 3; 18; …. В данном случае задание можно выполнить двумя способами, как по первой формуле, так и по второй, а затем выяснить, какой способ короче, а значит, рациональнее.

Способ №1 (по первой формуле): надо найти разность d, затем десятый член прогрессии, а затем сумму:

Способ №2 (по второй формуле): надо знать разность d, d=18-3=15. Теперь подставим значения во вторую формулу и сосчитаем результат:

Результаты в обоих случаях получились у нас одинаковые. А если сравнить два способа, то видно, что второй способ быстрее, тем более что в большинстве случаев разность арифметической прогрессии можно вычислить устно.

Таким образом, выбор формулы для нахождения суммы n первых членов арифметической прогрессии зависит от заданного условия.

-6-8=-14 через 1 минуту

-14-8=-22 через 2 минуты

-22-8=-30 через 3 минуты

-30-8=-38 через 4 минуты

-38-8=-46 через 5 минут

-46-8=-54 через 6 минут

Вторым способом является решение по формуле n-ого члена арифметической прогрессии, которая есть также и в справочном материале, т.е. a_n=a₁+d(n – 1). В данном случае a₁₌-6; d=-8, n=7 (так как ЧЕРЕЗ 6 минут). Подставим значения в формулу: a₇=-6₁-8(7 – 1). Вычислим: a₆=-6-8 ∙ 5=-6-48=-54.

pазбирался: Даниил Романович | обсудить разбор | оценить

Содержание данной задачи говорит нам о том, что здесь есть арифметическая прогрессия, так как число жителей города возрастало на одну и ту же величину.

2008 г – 38100 человек

2016 г. – 43620 человек

Итак, можно вычислить прирост населения с 2008 по 2016 ежегодно:

(43620 – 38100):(2016 – 2008)= 5520:8=690 человек.

Теперь можно найти, сколько человек проживало в конце 2012 года.

38100+690(2016 – 2012)= 40860 человек

pазбирался: Даниил Романович | обсудить разбор | оценить

pазбирался: Даниил Романович | обсудить разбор | оценить

В содержании задачи есть фраза, что акции дорожали ежедневно на одну и ту же сумму, следовательно, имеем арифметическую прогрессию. Итак, определяем, что известно: в 7-й день акция стоила 777 рублей, это а₇=777; в 12-й день – 852 рубля, это а₁₂=852. Известно, что акции дорожали 25 дней, а найти надо стоимость акции в последний, т.е. в 25-ый день, значит, будем искать а₂₅.

1 способ:

В данной арифметической прогрессии нет первого члена, не идет речь про сумму, поэтому воспользуемся формулой а_n=a_k+d(n – k), где n>k. Числа n и k – это порядковые номера. Составим формулу для наших данных и подставим в неё значения: а₁₂=а₇+d(12-7); 852=777+d(12 – 7). Упростим выражение и найдем разность d, 852–777= d(12 – 7); 75= d∙5; отсюда d=75:5=15. Итак, мы нашли, что акции ежедневно дорожали на 15 рублей.

Теперь, зная число d, мы можем найти а₂₅ через, например, а₁₂, используя всё ту же формулу. Получаем: а₂₅=а₁₂+d(25-12); а₂₅=852+15(25-12)=852+15∙13= 852+195=1047. Значит, 1047 рублей стоила акция в последний день.

2 способ:

pазбирался: Даниил Романович | обсудить разбор | оценить

В условии задачи встречаются слова, что норма увеличивалась на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой а₁=6, так как в первый день перевезли 6 тонн. Далее, известно, что вся работа была выполнена за 11 дней, значит число n=11. Так как масса всего щебня равна 176, то это число является суммой нашей прогрессии, т.е. S₁₁=176. Требуется найти, сколько тонн было перевезено в последний день, а он – 11, значит, найти надо а₁₁.

pазбирался: Даниил Романович | обсудить разбор | оценить

Из содержания данной задачи видно, что время процедуры увеличивалось с каждым днем на одно и то же количество времени – на 15 минут, следовательно, это арифметическая прогрессия. Так как в первый день курс был 15 минут, то а₁=15; так как время ежедневно увеличивалось на 15 минут, то значит разность d=15; зная, что продолжительность процедуры должна достигнуть 1 ч 15 мин, т.е. достигнуть 75 минут (1 час=60 мин, плюс 15 минут), то это число 75 и будет являться n членом арифметической прогрессии. Требуется найти, в какой по счету день продолжительность процедуры достигнет этих 75 минут, т.е. найдем число n.

Теперь берем формулу n члена арифметической прогрессии а_n=a₁+d(n – 1) и подставляем в неё наши данные: 75=15+15(n – 1); упростим данное выражение: 75-15=15(n – 1); 60=15(n – 1); разделим на 15 обе части: 4=n – 1; найдем отсюда, что n=5. Таким образом, на пятый день продолжительность процедуры достигнет 75 минут.

pазбирался: Даниил Романович | обсудить разбор | оценить

Анализируя содержание задачи, мы видим, что улитка проползала ежедневно на одно и то же расстояние меньше, чем в предыдущий день. А это значит, что имеем арифметическую прогрессию. По условию определяем данные: так как в первый и последний дни она проползла 7,5 м, то имеем, что а₁+а_n=7,5. Так как расстояние между деревьями равно 60 м, то имеем сумму n первых членов прогрессии, т.е. S_n=60. Так как найти надо количество дней, которое она потратила на весь путь, то искомым числом будет число n.

Зная формулу суммы n первых членов арифметической прогрессии

pазбирался: Даниил Романович | обсудить разбор | оценить

При анализе содержания задачи мы видим, что каждую минуту количество осадка увеличивается на одно и то же число, на 0,2 г. А это значит, что имеем арифметическую прогрессию, в которой первый член равен 0,2, так как по условию в первую минуту образовалось 0,2 г осадка. Разность арифметической прогрессии равна также 0,2, так как каждую минуту на это количество увеличивается количество осадков. Найти нужно седьмой член последовательности.

Итак, имеем а₁=0,2; d=0,2. Ищем а₇. По определению n-ого члена арифметической прогрессии имеем формулу а_n=a₁+d(n – 1). Подставим в нее наши данные: а₇=a₁+d(7 – 1)=0,2+0,2·6=1,4

pазбирался: Даниил Романович | обсудить разбор | оценить

Источник

• ← какую последовательность действий надо выполнить для запуска калькулятора в windows
• какую последовательность нужно применять при календарном планировании проекта →