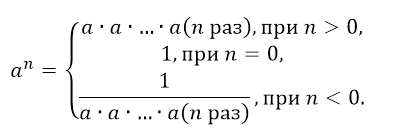какую функцию называют степенной

Алгебра и начала математического анализа. 10 класс

Конспект урока

Алгебра и начала математического анализа, 10 класс

Урок №18. Степенная функция. Дробно-линейная функция.

Перечень вопросов, рассматриваемых в теме

1) понятие степенной функции;

2) основные свойства функций и ;

3) понятия взаимно обратной и дробно- линейной функций;

4) особенности построения графика дробно-линейной функции.

Определение. Функция вида , где n- любое действительное число, называют степенной функцией.

Определение. Функцию y=f(x), x∈X называют обратимой, если любое своё значение она принимает только в одной точке множества X (иными словами, если разным значениям аргумента соответствуют разные значения функции).

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2014.

Шабунин М.И., Ткачева М.В., Федорова Н.Е. Дидактические материалы Алгебра и начала математического анализа (базовый и профильный уровни) 10 кл. – М.: Просвещение, 2017.

Теоретический материал для самостоятельного изучения

При n=1, y=x 1 или y=x — прямая (Рисунок 1).

Рисунок 1 – график функции y=x 1

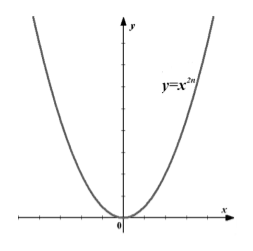
При n=2, y=x 2 — парабола.

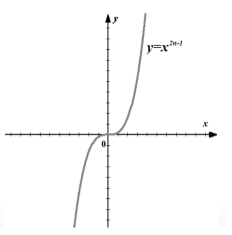
При n=3, y=x 3 — кубическая парабола.

Функции такого вида называются дробно-линейными.

Рассмотрим графики степенных функций y=x m/n с положительным дробным показателем m/n.

1. Степенная функция , где > неправильная дробь (числитель больше знаменателя).

График — ветвь параболы:

Рисунок 6 – , где

Свойства функции , где

3. не является ни чётной, ни нечётной;

4. возрастает при x∈[0;+∞);

5. не имеет наибольшего значения, y_наим=0;

6. не ограничена сверху, ограничена снизу;

2. Степенная функция , где — правильная дробь (числитель меньше знаменателя).

Свойства функции , где

3. не является ни чётной, ни нечётной;

4. возрастает при x∈[0;+∞);

5. не имеет наибольшего значения, y_наим=0;

6. не ограничена сверху, ограничена снизу;

Рассмотрим степенные функции с отрицательным дробным показателем степени

График — ветвь гиперболы.

График имеет горизонтальную асимптоту у=0 и вертикальную асимптоту х=0.

Свойства функции .

3. не является ни чётной, ни нечётной;

5. не имеет ни наибольшего, ни наименьшего значения;

6. не ограничена сверху, ограничена снизу;

Итак, на основании всего вышеперечисленного, можно сделать вывод в виде таблицы:

Рассмотрим еще одну функцию.

Определение. Функцию y=f(x), x∈X называют обратимой, если любое своё значение она принимает только в одной точке множества X (иными словами, если разным значениям аргумента соответствуют разные значения функции).

Если функция y=f(x), x∈X монотонна на множестве X, то она обратима.

Точки M(a;b) и P(b;a) симметричны относительно прямой y=x.

Нахождение формулы для функции, обратной данной

Пользуясь формулой y=f(x), следует выразить x через y, а в полученной формуле x=g(y) заменить x на y, а y на x.

Заданная функция возрастает на промежутке [0;+∞), значит, она имеет обратную функцию. Из уравнения y=x 2 находим: или . Промежутку [0;+∞) принадлежат лишь значения функции . Это и есть обратная функция, которая определена на промежутке [0;+∞).

Рисунок 9 – график функции, обратной y=x 2

Разборы и примеры решения заданий тренировочного модуля

Изобразите схематически график функции

Графиком данной функции является гипербола.

Источник

Функция. Степенная функция.

Так как нулевая степень всякого числа, не равного нулю, равна единице, то при n = 0 степенная функция становится постоянной величиной, т.е. у = а. Поясним подробнее: выражение ноль в нулевой степени неопределенно, в том случае, когда функция у = ax 0 для всех значений х, естественно кроме нуля, равна а, и следовательно, если х = 0, то у = а. В таком случае график представлен прямой линией, параллельной оси абсцисс).

Остальные случаи делятся на группы:

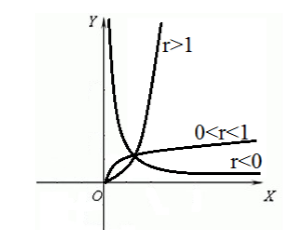
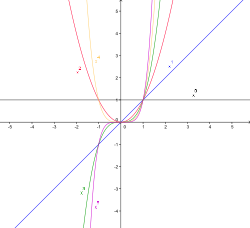
Видны графики функции у = х n при n = 0,1; 1/4; 1/3; 1/2; 2/3; 1;3/2; 2 ; 3; 4; 10. Все они проходят через начало координат и точку (1; 1).

При n = 1 получаем прямую являющуюся биссектрисой угла х0у.

При n > 1 график образуется сначала между х = 0 и х = 1, несколько ниже этой прямой, а затем при х > 1, выше ее.

По аналогии с графиком функции у = ах 2 графики всех степенных функций у = ах n при положительном n называют параболами n-го порядка или n-й степени. Так, график функции у = ах 3 называется параболой 3-го порядка или кубической параболой.

В случае если n дробное число p/q с четным знаменателем q и нечетным числителем р, то величина может иметь два знака , а у графика появляется еще одна часть внизу оси абсцисс х, причем она симметрична верхней части.

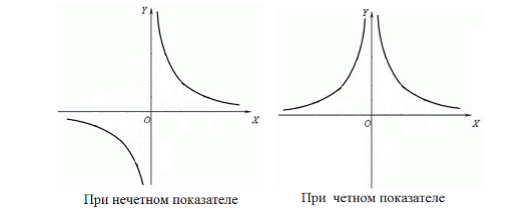
Все графики неограниченно приближаются как к оси абсцисс х, так и к оси ординат у, не соприкасаясь с ними. Вследствие сходства с гиперболой эти графики называют гиперболами n -го порядка.

Источник

Степенная функция

Вы будете перенаправлены на Автор24

Для удобства рассмотрения степенной функции будем рассматривать 4 отдельных случая: степенная функция с натуральным показателем, степенная функция с целым показателем, степенная функция с рациональным показателем и степенная функция с иррациональным показателем.

Степенная функция с натуральным показателем

Для начала введем понятие степени с натуральным показателем.

Рассмотрим теперь степенную функцию с натуральным показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in N)$ называется степенной функцией с натуральным показателем.

Свойства степенной функции с натуральным четным показателем

$f(x)\ge 0$ на всей области определения

Функция выпукла на всей области определения.

Поведение на концах области определения:

Готовые работы на аналогичную тему

Свойства степенной функции с натуральным нечетным показателем

Функция возрастает на всей области определения.

\[2\left(2n-1\right)\left(n-1\right)\cdot x^<2n-3>=0\] \[x=0\]

Степенная функция с целым показателем

Для начала введем понятие степени с целым показателем.

Рассмотрим теперь степенную функцию с целым показателем, её свойства и график.

$f\left(x\right)=x^n$ ($n\in Z)$ называется степенной функцией с целым показателем.

Свойства степенной функции с отрицательным целым показателем

Если показатель четный, то функция четна, если нечетный, то функция нечетна.

$f(x)\ge 0$ на всей области определения

Степенная функция с рациональным и иррациональным показателем

$f\left(x\right)=x^r$ ($r\in Q)$ называется степенной функцией с рациональным показателем.

$f\left(x\right)=x^r$ ($r\in J)$ называется степенной функцией с иррациональным показателем.

Приведем графики степенных функций с рациональным и иррациональным показателем (рис. 5). Рассмотреть, аналогично, свойства этих функции оставим читателю.

Источник

Степенная функция

Содержание

Вещественная функция

Область определения

Если показатель степени — целое число, то можно рассматривать степенную функцию на всей числовой прямой (кроме, возможно, нуля). В общем случае степенная функция определена при 0″ border=»0″ />. Если 0″ border=»0″ />, то функция определена также и при , иначе нуль является её особой точкой.

Рациональный показатель степени

Пример: из третьего закона Кеплера вытекает, что период T обращения планеты вокруг Солнца связан с большой полуосью A её орбиты соотношением: (полукубическая парабола).

Свойства

Комплексная функция

Степенная функция комплексного переменного z, вообще говоря, определяется формулой [3] :

Здесь показатель степени c — некоторое комплексное число. Значение функции, соответствующее главному значению логарифма, называется главным значением степени. Например, значение равно где k — произвольное целое, а его главное значение есть

Комплексная степенная функция обладает значительными отличиями от своего вещественного аналога. В силу многозначности комплексного логарифма она, вообще говоря, также имеет бесконечно много значений. Однако два практически важных случая рассматриваются отдельно.

См. также

Литература

Ссылки

Примечания

Полезное

Смотреть что такое «Степенная функция» в других словарях:

Степенная функция — функция f (x) = ха, где а фиксированное число (см. Степень). При действительных значениях основания х и показателя а обычно рассматривают лишь действительные значения С. ф. xa. Они существуют, во всяком случае, для всех х > 0; если а… … Большая советская энциклопедия

СТЕПЕННАЯ ФУНКЦИЯ — функция вида y = axn, где a и n любые действительные числа … Большой Энциклопедический словарь

СТЕПЕННАЯ ФУНКЦИЯ — ф ция вида у = ахn, где а и п действит. числа, С. ф. охватывает большое число закономерностей в природе. На рис. изображены графики С. ф. для п = 1, 2, 3, 1/2 и а = 1. К ст. Степенная функция … Большой энциклопедический политехнический словарь

степенная функция — функция вида у=axn, где а и n любые действительные числа. На рисунке изображены графики степенной функции для n = 1, 2, 3, 1/2 и а = 1. * * * СТЕПЕННАЯ ФУНКЦИЯ СТЕПЕННАЯ ФУНКЦИЯ, функция вида y = axn, где a и n любые действительные числа … Энциклопедический словарь

степенная функция — laipsninė funkcija statusas T sritis automatika atitikmenys: angl. power function vok. Potenzfunktion, f rus. степенная функция, f pranc. fonction puissance, f … Automatikos terminų žodynas

СТЕПЕННАЯ ФУНКЦИЯ — функция вида у = ахn, где а и п любые действительные числа. На рис. изображены графики С. ф. для n= 1, 2, 3, 1/2 и a=1 … Естествознание. Энциклопедический словарь

функция спроса — Функция, которая показывает, как меняется объем продаж конкретного продукта в зависимости от его цены при равных маркетинговых усилиях по его продвижению на рынок. [http://www.lexikon.ru/dict/fin/a.html] функция спроса Функция, отражающая… … Справочник технического переводчика

Функция спроса — [demand function] функция, отражающая зависимость объема спроса на отдельные товары и услуги (потребительские блага) от комплекса факторов, влияющих на него. Более узкая трактовка: Ф.с.выражает взаимозависимость между спросом на товар и ценой… … Экономико-математический словарь

Источник

Степенная функция, её свойства и график.

Ищем педагогов в команду «Инфоурок»

2) Область значений функции – множество неотрицательных чисел, если :

множество неположительных чисел, если :

На левом рисунке изображены примеры графиков степенных функций с чётным натуральным показателем, а на правом рисунке – графики тех же функций, но с растяжением и сжатием.

2) Область значений функции – множество всех действительных чисел: Е( y ) = (−; +).

3) Значит, функция является нечётной, её график симметричен относительно начала координат.

На левом рисунке изображены примеры графиков степенных функций с нечётным натуральным показателем, а на правом – графики тех же функций, но с растяжением и сжатием.

множество всех отрицательных чисел, если : Е( y ) = (-; 0).

Если функция убывает при х (- ; 0), возрастает при х (0; + ).

На первом рисунке изображены примеры графиков степенных функций с чётным целым отрицательным показателем, а на втором рисунке – графики тех же функций, но с растяжением и сжатием.

1) Область определения функции:

2) Область значений функции:

3) Значит, функция является нечётной, её график симметричен относительно начала координат.

На левом рисунке изображены примеры графиков степенных функций с нечётным целым отрицательным показателем, а на правом рисунке – графики тех же функций, но с растяжением и сжатием.

1) Областью определения функции, исходя из определения степени с рациональным показателем, является множество неотрицательных чисел:

3) Функция не является ни чётной, ни нечётной, так как её область определения не содержит противоположных значений.

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде положительной правильной дроби и графики тех же функций, но с растяжением и сжатием.

1) Областью определения функции, исходя из определения степени с рациональным показателем, является множество неотрицательных чисел:

3) Функция не является ни чётной, ни нечётной, так как её область определения не содержит противоположных значений.

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде положительной неправильной дроби и графики тех же функций, но с растяжением и сжатием.

1) Областью определения функции, исходя из определения степени с рациональным показателем, является множество неотрицательных чисел:

3) Функция не является ни чётной, ни нечётной, так как её область определения не содержит противоположных значений.

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде отрицательной правильной дроби и графики тех же функций, но с растяжением и сжатием.

1) Областью определения функции, исходя из определения степени с рациональным показателем, является множество неотрицательных чисел:

3) Функция не является ни чётной, ни нечётной, так как её область определения не содержит противоположных значений.

4) Если функция убывает при х ;

На рисунке изображены примеры графиков степенных функций с показателем, представленным в виде отрицательной неправильной дроби и графики тех же функций, но с растяжением и сжатием.

Источник