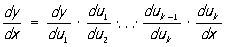какую функцию называют сложной

Сложная функция. Производная сложной функции

Раз ты зашел сюда, то уже, наверное, успел увидеть в учебнике эту формулу

и сделать вот такое лицо:

Друг, не переживай! На самом деле все просто до безобразия. Ты обязательно все поймешь. Только одна просьба – прочитай статью не торопясь, старайся понять каждый шаг. Я писал максимально просто и наглядно, но вникнуть в идею всё равно надо. И обязательно реши задания из статьи.

Что такое сложная функция?

Представь, что ты переезжаешь в другую квартиру и поэтому собираешь вещи в большие коробки. Пусть надо собрать какие-нибудь мелкие предметы, например, школьные письменные принадлежности. Если просто скидать их в огромную коробку, то они затеряются среди других вещей. Чтобы этого избежать, ты сначала кладешь их, например, в пакет, который затем укладываешь в большую коробку, после чего ее запечатываешь. Этот «сложнейший» процесс представлен на схеме ниже:

Например, возьмем x и «запакуем» его в функцию косинуса :

Что получится в итоге? Да, верно, будет «пакет с вещами в коробке», то есть «косинус икса в кубе».

В школьном курсе видов этих самых «упаковок» совсем мало, всего четыре :

Напиши теперь сам функции, где икс:
— сначала «упаковывается» в косинус, а потом в показательную функцию с основанием \(3\);
— сначала в пятую степень, а затем в тангенс;
— сначала в логарифм по основанию \(4\) , затем в степень \(-2\).

Ответы на это задание посмотри в конце статьи.

А можем ли мы «упаковать» икс не два, а три раза? Да, без проблем! И четыре, и пять, и двадцать пять раз. Вот, например, функция, в которой икс «упакован» \(4\) раза:

«Распаковка» сложной функции

Теперь правильный ответ: сначала икс «упаковали» в \(4\)-ую степень, потом результат упаковали в синус, его в свою очередь поместили в логарифм по основанию \(2\), и в конце концов всю эту конструкцию засунули в степень пятерки.

То есть разматывать последовательность надо В ОБРАТНОМ ПОРЯДКЕ. И тут подсказка как это делать проще: сразу смотри на икс – от него и надо плясать. Давай разберем несколько примеров.

\(x → \log_2⁡x → tg⁡(\log_2⁡x )\)

Еще пример: \(y=\cos⁡<(x^3 )>\). Анализируем – сначала икс возвели в куб, а потом от результата взяли косинус. Значит, последовательность будет: \(x → x^3 → \cos⁡<(x^3 )>\). Обрати внимание, функция вроде бы похожа на самую первую (там, где с картинками). Но это совсем другая функция: здесь в кубе икс (то есть \(\cos⁡<(x·x·x)>)\), а там в кубе косинус \(x\) (то есть, \(\cos⁡x·\cos⁡x·\cos⁡x\)). Эта разница возникает из-за разных последовательностей «упаковки».

Последний пример (с важной информацией в нем): \(y=\sin⁡<(2x+5)>\). Понятно, что здесь сначала сделали арифметические действия с иксом, потом от результата взяли синус: \(x → 2x+5 → \sin⁡<(2x+5)>\). И это важный момент: несмотря на то, что арифметические действия функциями сами по себе не являются, здесь они тоже выступают как способ «упаковки». Давай немного углубимся в эту тонкость.

Однако если к такой комбинации применить еще одну функцию – будет уже сложная функция, так как «упаковок» станет две. Смотри схему:

Хорошо, давай теперь сам. Напиши последовательность «заворачивания» функций:
\(y=cos<⁡(sin⁡x)>\)
\(y=5^\)
\(y=arctg⁡<11^x>\)
\(y=log_2⁡(1+x)\)
Ответы опять в конце статьи.

Внутренняя и внешняя функции

Зачем же нам нужно разбираться во вложенности функций? Что нам это дает? Дело в том, что без такого анализа мы не сможем надежно находить производные разобранных выше функций.

Вот в этом примере: \(y=tg⁡(log_2⁡x )\), функция \(\log_2⁡x\) – внутренняя, а — внешняя.

Заполни пропуски в таблице:

Производная сложной функции

Браво нам, мы всё ж таки добрались до «босса» этой темы – собственно, производной сложной функции, а конкретно, до той самой ужасной формулы из начала статьи.☺

Формула эта читается так:

Производная сложной функции равна произведению производной внешней функции по неизменной внутренней на производную внутренней функции.

И сразу смотри схему разбора «по словам» чтобы понимать, что к чему относится:

Ответ: это обычная производная внешней функции, при которой изменяется только внешняя функция, а внутренняя остается такой же. Все равно непонятно? Хорошо, давай на примере.

Пусть у нас есть функция \(y=\sin⁡(x^3 )\). Понятно, что внутренняя функция здесь \(x^3\), а внешняя . Найдем теперь производную внешней по неизменной внутренней.

Тогда производная внешней функции по неизменной внутренней для нашего случая будет \(\cos⁡(x^3)\). То есть, мы взяли ее как обычную производную синуса, а содержимое синуса (внутреннюю функцию) просто скопировали в полученную производную (косинус), ничего в ней не меняя.

Таким образом, на данный момент имеем:

Осталась «производная внутренней функции». Ну, это совсем легко – обычная производная от внутренней функции, при этом внешняя не влияет вообще никак. В нашем примере, производная от \(x^3\).

Все, теперь можем писать ответ:

Вот так. Давай еще один пример разберем.

Пусть надо найти производную функции \(y=(\sin⁡x )^3\).

Анализируем. Последовательность «заворачивания» у нас такая: \(x → \sin⁡x → (\sin⁡x )^3\). Значит, в данном примере внутренняя функция это \(\sin⁡x\), а внешняя .

Производная внешней по внутренней – это производная куба (содержимое куба при этом не меняется). Так как , а в нашем случае в куб «завернут» \(\sin⁡x\), то производная внешней будет \(3(\sin⁡x)^2\). То есть, имеем:

Ну, а производная внутренней – это просто производная синуса икс, то есть косинус икс.

Понятно?
Ладно, ладно, вот еще один пример с разбором. ☺

Пример. Найти производную сложной функции \(y=\ln(x^2-x)\).

Ну и напоследок можно немного «причесать» ответ, чтоб никто не докопался:

Что, еще примеров желаешь? Легко.

Еще пример с важным замечанием в нем.

Пример. Найти производную сложной функции \(y=\sqrt \)
Вложенность функций: \(x → x^6 → \sqrt\)
Внутренняя: \(x^6\) Внешняя:
Производная внешней по внутренней: \(\sqrt‘=\) \(\frac<1><2\sqrt>\)
Производная внутренней: \((x^6)’= 6x^5\)
Имеем: \((\sqrt)’=\) \(\frac<1><2\sqrt>\) \(·6x^5\)
И теперь упростим ответ. Вспомним свойство корня: \(\sqrt[b] =x^<\frac>\). Тогда \(\sqrt=x^<\frac<6><2>>=x^3\). С учетом этого получаем:

Всё. А теперь, собственно, важное замечание:

Давай рассмотрим пример, где эта идея нам сильно поможет.

Пример. Найти производную сложной функции \(y=\ln⁡(x^3)\).
Можно, конечно, рассмотреть вложенность функций: \(x → x^3 → \ln⁡(x^3 )\), разобрать на внутреннюю и внешнюю и так далее. Но можно вспомнить свойство логарифма: \(\log_a⁡=c·\log_a<⁡b>\). И тогда функция получается \(y=\ln⁡(x^3 )=3\ln⁡x\). Отлично! Берем производную:

Теперь задачка посложнее, для продвинутых. Решим пример с тройной вложенностью!

Пример. Найти производную сложной функции \(y=3^<\sin⁡(x^4+1)>\).
Вложенность функций: \(x → x^4+1 → \sin⁡(x^4+1) → 3^<\sin⁡(x^4+1)>\)
Внутренняя: \(x^4+1\) Средняя: Внешняя:
Сначала производная внешней по средней. Вспоминаем таблицу производных: . Значит, в нашем случае будет \(3^<\sin⁡(x^4+1)>·\ln⁡3\).
Хорошо, теперь производная средней по внутренней. По таблице: . Значит, мы получим, \(\sin⁡(x^4+1)’=\cos⁡(x^4+1)\).
И наконец, производная внутренней: \((x^4+1)’=(x^4 )’+(1)’=4x^3\).
Отлично. Теперь собираем все вместе, перемножая отдельные производные:

Готово. Да, это ответ. ☺

Ну, а что ты хотел, я сразу сказал – пример для продвинутых! А представь, что будет с четырехкратной или пятикратной вложенностью? ☺

Пример: Найти производную сложной функции \(y=tg⁡(7^x)\).

Ну, теперь думаю всё понятно? И снова повторю – не пугайся сложных конструкций в ответах и промежуточных вычислениях. Они «на лицо ужасные», но зато добрые (в смысле простые) внутри. ☺ Пойми принцип и делай все последовательно.

Последний пример. Такие задания в разных вариациях весьма часто дают на контрольных и тестах. Он вроде как считается сложным. ☺ Хех, наивные учителя. ☺

Пример: Найти производную сложной функции \(y=\sqrt[3]<(x^5+2x-5)^2>\).

Казалось бы, опять у нас тройная вложенность функций:

Но давай снова воспользуемся свойством корня \(\sqrt[b] =x^<\frac>\) и преобразуем нашу функцию к виду:

Вот так. И теперь у нас вложенность двойная: \(x → x^5+2x-5 → (x^5+2x-5)^<\frac<2><3>>\)
При этом функция осталась той же! Удобное свойство, однако. Стоит его запомнить, да? ☺ Ладно, поехали дальше.
Внутренняя функция: \(x^5+2x-5\). Внешняя: .
Производная внешней по внутренней. По таблице производных общая формула производной степенной функции: . Получаем: . Тогда в нашем случае будет: \(\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>\).
Производная внутренней: \((x^5+2x-5)’=5x^4+2\).
Общий результат: \(y ‘=(\sqrt[3]<(x^5+2x-5)^2>)’=((x^5+2x-5)^<\frac<2><3>> )’=\frac<2><3>(x^5+2x-5)^<-\frac<1><3>>·(5x^4+2)\).

Ну, и перемножаем дроби.

Найти производные функций:

Ответы ко всем заданиям (вперемежку).

\(x → 1+x → \log_2⁡ <(1+x)>\)
\(x → 11^x → arctg⁡(11^x) \)
\(x → x^7 → 5^\)
\(x → \sin⁡x → \cos⁡(\sin⁡x)\)

Источник

Производная сложной функции

Данная статья покажет понятие сложной функции и ее выявление. Поработаем с формулами нахождения производной с примерами решений в заключении. Применение таблицы производных и правила дифференцирования заметно уменьшают время для нахождения производной.

Основные определения

Сложной функцией считается такая функция, у которой аргумент также является функцией.

Понятие композиция функции относится к количеству вложенных функций по условию задачи. Для решения используется формула нахождения производной сложной функции вида

( f ( g ( x ) ) ) ‘ = f ‘ ( g ( x ) ) · g ‘ ( x )

Примеры

По условию видно, что f является функцией возведения в квадрат, а g ( x ) = 2 x + 1 считается линейной функцией.

Применим формулу производной для сложной функции и запишем:

Необходимо найти производную с упрощенным исходным видом функции. Получаем:

y = ( 2 x + 1 ) 2 = 4 x 2 + 4 x + 1

Первая запись функции говорит о том, что f является функцией возведения в квадрат, а g ( x ) – функцией синуса. Тогда получим, что

Вторая запись показывает, что f является функцией синуса, а g ( x ) = x 2 обозначаем степенную функцию. Отсюда следует, что произведение сложной функции запишем как

Из формулы определения сложной функции имеем, что

y ‘ = f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ‘ ( f 3 ( f 4 ( x ) ) ) · f 3 ‘ ( f 4 ( x ) ) · f 4 ‘ ( x )

Получаем, что следует найти

Производим объединение промежуточных результатов и получаем, что

y ‘ = f ‘ ( f 1 ( f 2 ( f 3 ( f 4 ( x ) ) ) ) ) · f 1 ‘ ( f 2 ( f 3 ( f 4 ( x ) ) ) ) · · f 2 ‘ ( f 3 ( f 4 ( x ) ) ) · f 3 ‘ ( f 4 ( x ) ) · f 4 ‘ ( x ) = = cos ( ln 3 a r c t g ( 2 x ) ) · 3 · ln 2 a r c t g ( 2 x ) · 1 a r c t g ( 2 x ) · 1 1 + 4 x 2 · 2 = = 6 · cos ( ln 3 a r c t g ( 2 x ) ) · ln 2 a r c t g ( 2 x ) a r c t g ( 2 x ) · ( 1 + 4 x 2 )

Разбор таких функций напоминает матрешки. Правила дифференцирования не всегда могут быть применены в явном виде при помощи таблицы производных. Зачастую нужно применять формулу нахождения производных сложных функций.

Существуют некоторые различия сложного вида от сложных функций. При явном умении это различать, нахождение производных будет давать особенно легко.

y ‘ = ( t g x 2 + 3 t g x + 1 ) ‘ = ( t g x 2 ) ‘ + ( 3 t g x ) ‘ + 1 ‘ = = ( t g x 2 ) ‘ + 3 · ( t g x ) ‘ + 0 = ( t g x 2 ) ‘ + 3 cos 2 x

Переходим к нахождению производной сложной функции ( t g x 2 ) ‘ :

Получаем, что y ‘ = ( t g x 2 + 3 t g x + 1 ) ‘ = ( t g x 2 ) ‘ + 3 cos 2 x = 2 x cos 2 ( x 2 ) + 3 cos 2 x

Функции сложного вида могут быть включены в состав сложных функций, причем сами сложные функции могут являться составными функции сложного вида.

Для примера рассмотрим сложную функцию вида y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 )

Отсюда видно, что h ( x ) = l ( x ) m ( x ) = n ( x ) + p ( x ) q ( x ) + r ( x ) = n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) + r ( x )

y = log 3 x 2 + 3 cos 3 ( 2 x + 1 ) + 7 e x 2 + 3 3 + ln 2 x · ( x 2 + 1 ) = = f n ( x ) + 3 · p 1 ( p 2 ( p 3 ( x ) ) ) q 1 ( q 2 ( x ) ) = r ( x ) + s 1 ( s 2 ( x ) ) · t ( x )

По структурам функции стало явно, как и какие формулы необходимо применять для упрощения выражения при его дифференцировании. Для ознакомления подобных задач и и для понятия их решения необходимо обратиться к пункту дифференцирования функции, то есть нахождения ее производной.

Источник

Лекция по математике на тему «Сложная и обратная функции»

Ищем педагогов в команду «Инфоурок»

Лекция: Сложная функция. Обратная функция.

Преподаватель: Горячева А.О.

Функция – соответствие между множествами (Х и У), при котором каждому элементу первого множества (Х) соответствует не более одного элемента другого множества (У).

Представим это наглядно:

Формула для задания сложной функции:

Задание 1: В указанных сложных функциях назовите внешнюю и внутреннюю функции:

1). y = sin2x; 2) y = (x 3 – 1 ) 5 ; 3) y = cos(7x + 2); y = sin 2 x + 5sinx.

Привести пример с законом Ома для участка цепи: знаем напряжение – находим силу тока. Как зная силу тока найти напр.?

Пусть дана возрастающая или убывающая функция y= f(x), определенная на некотором отрезке [a; b]. Для определенности будем рассматривать возрастающую функцию (для убывающей все аналогично).

Рассмотрим два различных значения х1 и х2. Пусть y1=f(x1), y2=f(x2). Из определения возрастающей функции следует, что если x1

Эта функция называется обратной для функции y=f(x). Очевидно, что и функция y=f(x) является обратной для функции x=g(у).

Обратная функция x=g(y) находится путем решения уравнения y=f(x) относительно х.

Не каждая функция имеет обратную.

Замечание : монотонность функции, является достаточным условием существования обратной функции. Но оно не является необходимым условием.

Примеры различных ситуаций, когда функция не монотонна, но обратима, когда функция не монотонна и не обратима, когда монотонна и обратима

Убедиться, что функция монотонна.

Выразить переменную х через у.

Пример 1: Показать, что для функции y=5x-3 существует обратная функция, и найти ее аналитическое выражение.

Решение. Линейная функция y=5x-3 определена на R, возрастает на R и область ее значений есть R. Значит, обратная функция существует на R. Чтобы найти ее аналитическое выражение, решим уравнение y=5x-3 относительно х; получим Это и есть искомая обратная функция. Она определена и возрастает на R.

Функция непрерывна, монотонна в своей области определения, следовательно, она обратима. Проанализировав области определения и множества значений функции, делается соответствующий вывод об аналитическом выражении для обратной функции.

Ответ:

Источник

Таблица производных функций

10 класс, 11 класс, ЕГЭ/ОГЭ

Что такое производная и зачем она нужна

Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:

Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.

Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.

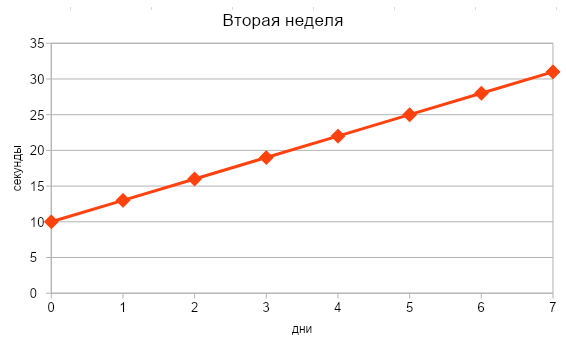
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:

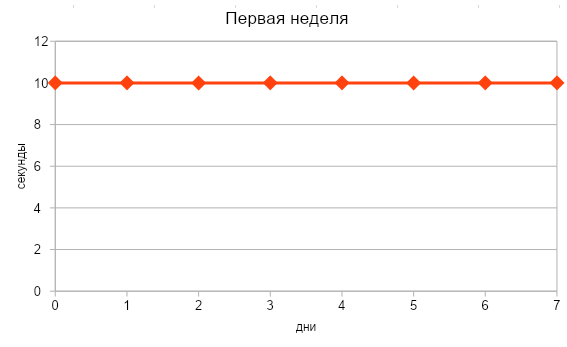
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.

Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.

Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.

Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.

Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.

Производные основных элементарных функций

Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Приведем несколько формул, которых достаточно для решения большинства задач.

Источник

Сложная функция

Смотреть что такое «Сложная функция» в других словарях:

сложная функция — — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом EN composite function … Справочник технического переводчика

сложная функция — функция от функции. Если величина у является функцией от u, то есть у = f(u), а u, в свою очередь, функцией от х, то есть и = φ(х), то у=F(х) является сложной функцией от х, то есть y=F(x)=f[φ(x)]. * * * СЛОЖНАЯ ФУНКЦИЯ СЛОЖНАЯ ФУНКЦИЯ, функция… … Энциклопедический словарь

СЛОЖНАЯ ФУНКЦИЯ — функция, представленная как композиция нескольких функций. Если множество значений Yi функции fi содержится во множестве определения Х i+1 функции fi+1, т. е. то функция определяемая равенством наз. сложной функцией или (п 1) кратной композицией… … Математическая энциклопедия

СЛОЖНАЯ ФУНКЦИЯ — функция от функции. Если величина у является функцией от и, то есть у = f(u), а и, в свою очередь, функцией от х, то есть u = ф(х), то y = F(x) является С. ф. от х, то есть y = F(x) = f[ф(x)] … Естествознание. Энциклопедический словарь

Сложная функция — … Википедия

Сложная трёхчастная форма — Сложная трёхчастная форма музыкальная репризная трёхчастная форма, первая часть которой сложнее периода. Чаще всего первая часть представляет собой простую двух или трёхчастную форму, но иногда бывает и сложнее (кроме того, средний раздел… … Википедия

МОДУЛЯРНАЯ ФУНКЦИЯ — эллиптическая модулярная функция, одного комплексного переменного автоморфная функция комплексного переменного ассоциированная с группой Г всех дробно линейных преобразований вида где целые действительные числа (эта группа наз. модулярной).… … Математическая энциклопедия

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ — раздел математики, в к ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу… … Математическая энциклопедия

АБСОЛЮТНАЯ НЕПРЕРЫВНОСТЬ — 1) А. н. интеграла свойство неопределенного интеграла (Лебега). Пусть функция f интегрируема на множестве Е. Интеграл от f на измеримых подмножествах является абсолютно непрерывной функцией (см. ниже п. 3) множества относительно меры m, т. е. для … Математическая энциклопедия

Источник