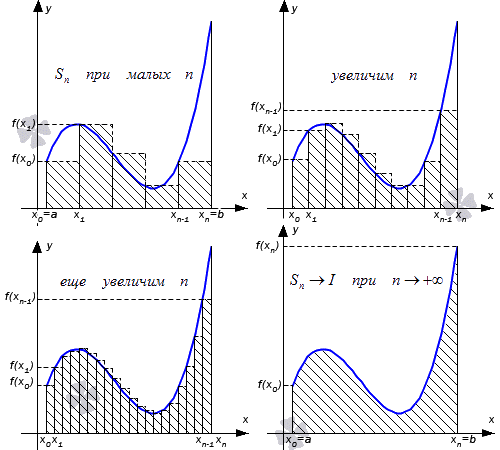
какую функцию можно интегрировать

Классы интегрируемых функций

Классы интегрируемых функций

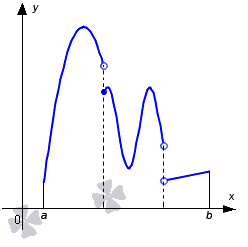
Классы интегрируемых функций. Примените найденную функциональность к созданию интегрируемой функции для определенного класса. I. Если функция f (x) непрерывна на интервале[a, b \ y, то она интегрируема. Доказательство. Поскольку функция f (x) непрерывна, то только интервал[a, b) разбивается на части с длиной, основанной на индуктивном методе теоремы Кантора[n°7b]при заданном e> 0, и отсюда он делится на две части. с-1 с-1 ^ а> а* > 2 ДХ,= W(В-а). Ио = 0 так как b-a является постоянной величиной, а e произвольно мало, то условие(8) выполняется, и существование интеграла следует за ним. Вы можете обобщить некоторые из проверенных утверждений. I. Доказательство ограничивается случаем, когда существует только 1 точка разрыва n /между a и b(рис.66).Возьмем любой e> 0.

Если число точек разрыва, содержащихся в ограниченной функции, конечно, то оно интегрируемо. Людмила Фирмаль

Наконец, он показывает еще один простой класс функций, которые могут быть интегрированы, которые не были охвачены в предыдущем. Людмила Фирмаль

Если вам потребуется помощь по математическому анализу вы всегда можете написать мне в whatsapp.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник

Интегралы для чайников: как решать, правила вычисления, объяснение

Решение интегралов – задача легкая, но только для избранных. Эта статья для тех, кто хочет научиться понимать интегралы, но не знает о них ничего или почти ничего. Интеграл. Зачем он нужен? Как его вычислять? Что такое определенный и неопределенный интегралы?

Если единственное известное вам применение интеграла – доставать крючком в форме значка интеграла что-то полезное из труднодоступных мест, тогда добро пожаловать! Узнайте, как решать простейшие и другие интегралы и почему без этого никак нельзя обойтись в математике.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Изучаем понятие « интеграл »

Интегрирование было известно еще в Древнем Египте. Конечно, не в современном виде, но все же. С тех пор математики написали очень много книг по этой теме. Особенно отличились Ньютон и Лейбниц, но суть вещей не изменилась.

Как понять интегралы с нуля? Никак! Для понимания этой темы все равно понадобятся базовые знания основ математического анализа. Сведения о пределах и производных, необходимые и для понимания интегралов, уже есть у нас в блоге.

Неопределенный интеграл

Пусть у нас есть какая-то функция f(x).

Неопределенным интегралом функции f(x) называется такая функция F(x), производная которой равна функции f(x).

Другими словами интеграл – это производная наоборот или первообразная. Кстати, о том, как вычислять производные, читайте в нашей статье.

Первообразная существует для всех непрерывных функций. Также к первообразной часто прибавляют знак константы, так как производные функций, различающихся на константу, совпадают. Процесс нахождения интеграла называется интегрированием.

Простой пример:

Чтобы постоянно не высчитывать первообразные элементарных функций, их удобно свести в таблицу и пользоваться уже готовыми значениями.

Полная таблица интегралов для студентов

Определенный интеграл

Имея дело с понятием интеграла, мы имеем дело с бесконечно малыми величинами. Интеграл поможет вычислить площадь фигуры, массу неоднородного тела, пройденный при неравномерном движении путь и многое другое. Следует помнить, что интеграл – это сумма бесконечно большого количества бесконечно малых слагаемых.

В качестве примера представим себе график какой-нибудь функции.

Как найти площадь фигуры, ограниченной графиком функции? С помощью интеграла! Разобьем криволинейную трапецию, ограниченную осями координат и графиком функции, на бесконечно малые отрезки. Таким образом фигура окажется разделена на тонкие столбики. Сумма площадей столбиков и будет составлять площадь трапеции. Но помните, что такое вычисление даст примерный результат. Однако чем меньше и уже будут отрезки, тем точнее будет вычисление. Если мы уменьшим их до такой степени, что длина будет стремиться к нулю, то сумма площадей отрезков будет стремиться к площади фигуры. Это и есть определенный интеграл, который записывается так:

Точки а и b называются пределами интегрирования.

Бари Алибасов и группа

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Правила вычисления интегралов для чайников

Свойства неопределенного интеграла

Как решить неопределенный интеграл? Здесь мы рассмотрим свойства неопределенного интеграла, которые пригодятся при решении примеров.

Свойства определенного интеграла

Как считать определенный интеграл? С помощью формулы Ньютона-Лейбница.

Мы уже выяснили, что определенный интеграл – это предел суммы. Но как получить конкретное значение при решении примера? Для этого существует формула Ньютона-Лейбница:

Примеры решения интегралов

Ниже рассмотрим неопределенный интеграл и примеры с решением. Предлагаем самостоятельно разобраться в тонкостях решения, а если что-то непонятно, задавайте вопросы в комментариях.

Для закрепления материала посмотрите видео о том, как решаются интегралы на практике. Не отчаиваетесь, если интеграл не дается сразу. Обратитесь в профессиональный сервис для студентов, и любой тройной или криволинейный интеграл по замкнутой поверхности станет вам по силам.

Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.

Источник

Определенный интеграл Римана, Дарбу, Ньютона-Лейбница, виды интегрируемых функций

После обобщения выражения и определения получили, что любая непрерывная функция y = f ( x ) с числом I имеет отрезок, который и получил название определенного интеграла.

Его геометрическое понятие было показано в школе в 11 классе. Рассмотрим рисунок, приведенный ниже. Имеем изображение определенного интеграла.

В данной статье будет показано определения определенного интеграла, которые были заданы Риманом и Дарбу, Ньютоном-Лейбницом. Подробно будет показано условие интегрируемости функции на заданном определенном отрезке с перечислением интегрируемых функций.

Определенный интеграл Римана

Рассмотрим рисунок, приведенный ниже.

Числа a и b называют нижним и верхним пределом интегрирования, а f ( x ) – подынтегральная функция, где x – переменная интегрирования.

Определенный интеграл Дарбу

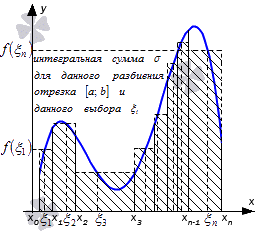
Чтобы понять необходимо и достаточное условие существования определенного интеграла Дарбу, необходимо применить несколько определений.

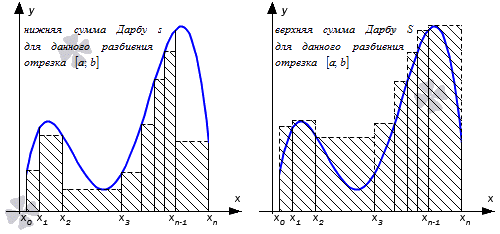
для разбиения отрезка [ a ; b ] называют нижней и верхней суммами Дарбу.

Рассмотрим рисунок, приведенный ниже.

Определенный интеграл Ньютона-Лейбница

Рассмотрим подробно понятие определенного интеграла Ньютона-Лейбница.

Необходимое условие интегрируемости функции на отрезке, виды интегрируемых функций

Рассмотрим необходимое условие существования определенного интеграла функции на отрезке.

Виды функций, для которых существует определенный интеграл:

Рассмотрим рисунок, приведенный ниже. На нем располагается пример интегрируемой функции.

Итоги

Задавание определенного интеграла Римана происходит через предел интегральных сумм, а интеграл Дарбу – предел разности верхних и нижних сумм Дарбу, в свою очередь интеграл Ньютона-Лейбница – при помощи значения первообразной.

Источник

Определение и условия существования определенного интеграла

Задачи, приводящие к понятию определенного интеграла.

Площадь криволинейной трапеции.

Пусть функция \(f\) непрерывна на отрезке \(\Delta = [a, b]\) и неотрицательна, то есть \(f(x) \geq 0\) при всех \(x \in \Delta\). Рассмотрим фигуру \(G\) (рис. 34.1), ограниченную отрезками прямых \(x = a,\ x = b,\ y = 0\) и графиком функции \(y = f(x)\), то есть
$$
G = \<(x, y): a \leq x \leq b,\ 0 \leq y \leq f(x)\>.\nonumber
$$

Такую фигуру называют криволинейной трапецией, а отрезок \(\Delta\) — ее основанием.

Рис. 34.1

Разобьем отрезок \(\Delta\) на \(n\) частей точками \(x_(i = \overline<1, n-1>)\), где \(x_ <1>Пример 1.

Найти площадь фигуры, ограниченной параболой \(y = x^<2>\) и отрезками прямых \(x = a\), где \(a > 0\), и \(y = 0\) (рис. 34.2).

\(\triangle\) Пользуясь тем, что предел суммы \(\sigma\) для непрерывной функции \(f(x) = x^<2>\) (см. раздел «Классы интегрируемых функций») не зависит от способа дробления отрезка \(\Delta = [0, a]\) и выбора точек \(\xi_\) будем считать, что отрезок \(\Delta\) разбит на \(n\) отрезков равной длины, а в качестве точки \(\xi_\ (i = \overline<1, n>)\) взят правый конец отрезка \(\Delta_\). Тогда \(\xi_ = x_ = \displaystyle \fraci,\ \Delta x_ = \frac,\ \sigma = \sum_ <\substack>^<\substack>x_^<2>\Delta x_ = \frac>>\sum_ <\substack>^<\substack>i^<2>\).

Так как \(\displaystyle \sum_^i^ <2>= \frac<6>\) (доказательство представлено здесь), то \(\sigma =\displaystyle \frac><3>\left(1 + \frac<1>\right)\left(1 + \frac<1><2n>\right)\), откуда \(\displaystyle \lim_ \sigma = \frac><3>\). Поэтому искомая площадь равна \(\displaystyle \frac><3>\). \(\blacktriangle\)

Заметим, что этот результат был получен еще Архимедом с помощью предельного перехода. Существует также простой способ нахождения предела для \(\sigma\), основанный на формуле Ньютона Лейбница.

Работа переменной силы.

Пусть материальная точка движется вдоль числовой прямой \(Ox\) под действием силы \(P\), причем направление действия силы совпадает с направлением движения материальной точки. Предположим, что сила \(P\) задана как непрерывная функция от координаты \(x\) этой прямой, то есть \(P = P(x)\).

Найдем работу силы \(P\) при перемещении материальной точки от \(x = a\) до \(x = b\). Разобьем отрезок [\(a, b\)], как и в задаче о площади криволинейной трапеции, точками \(x_\) и выберем \(\xi_ \in \Delta_ (i = \overline<1, n>)\). Тогда работа силы \(P\) на отрезке \(\Delta_\) приближенно равна \(P(\xi_)\Delta x_\), а на отрезке [\(a, b\)] работу этой силы можно считать приближенно равной сумме \(\displaystyle \sum_^P(\xi_)\Delta x_\). Предел этой суммы (при тех же условиях, что и в задаче о площади) естественно назвать работой переменной силы при перемещении материальной точки из точки \(a\) в точку \(b\).

В рассмотренных задачах речь идет о нахождении предела сумм вида \(\displaystyle \sum_^f(\xi_)\Delta x_\), которые называют интегральными суммами. К вычислению предела таких сумм сводится решение многих важных задач из геометрии, физики, техники и других дисциплин. Поэтому вопросы, связанные с обоснованием предельного перехода описанного типа, заслуживают всестороннего изучения.

Понятие определенного интеграла.

Пусть функция одного переменного \(f(x)\) определена на отрезке [\(a, b\)] и пусть \(x_ (i = \overline<0, n>)\) — совокупность точек этого отрезка таких, что
$$
a = x_ <0>Определение.

Если существует число \(J\), определяемое условиями \eqref, то функцию \(f\) называют интегрируемой (по Риману) на отрезке \([a, b]\) и говорят, что существует интеграл от функции \(f\) на отрезке \([a, b]\).

Источник

Интегрирование

Интегрирование

Пример. По таблице производных можно восстановить интегралы следующего вида: .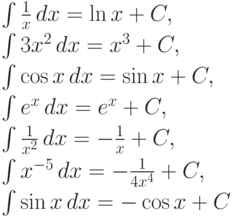

Используя таблицу производных, можно записать (и нужно запомнить) следующую таблицу неопределенных интегралов:

Используя свойства неопределенных интегралов и таблицу основных интегралов, можно интегрировать некоторые функции.

Пример. Нетрудно проверить справедливость следующих равенств:

Правил для интегрирования произведения, частного, сложной, обратной функции в общем случае нет. Имеются лишь отдельные приемы интегрирования некоторых классов функции.

Основные рекомендации по интегрированию можно свести к следующим основным правилам.

В качестве функции u следует выбирать ту из функций f, g которая имеет более простую производную, а за dv принимать дифференциал той функции из них, который будет легко интегрироваться.

Для получения окончательного результата приходится часто несколько раз последовательно применять формулу интегрирования по частям.

Пример. .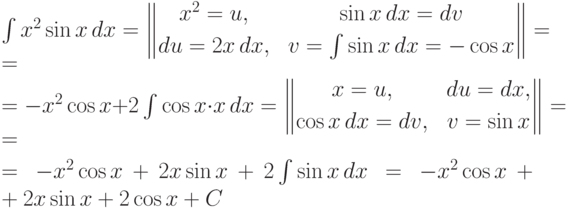

Здесь в двойные вертикальные линии заключены все вычисления, которые являются подготовительными для применения формулы интегрирования по частям.

Источник