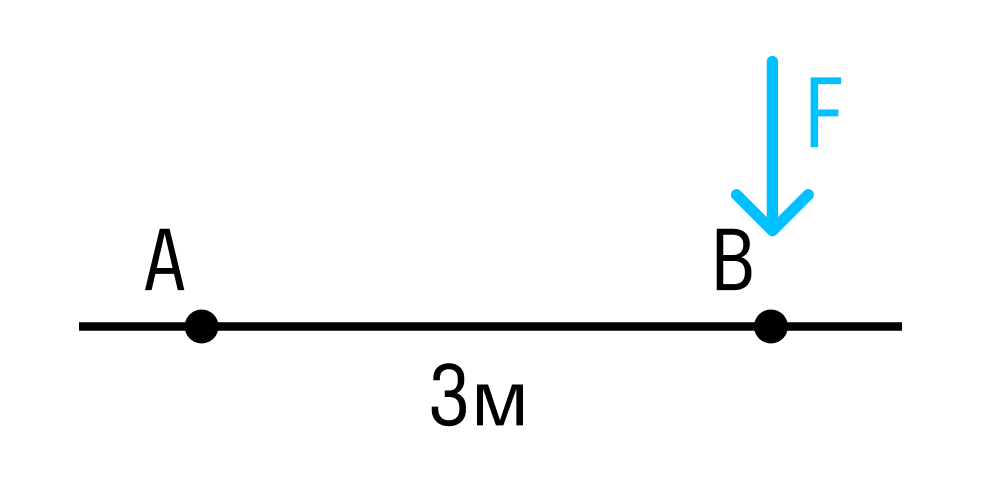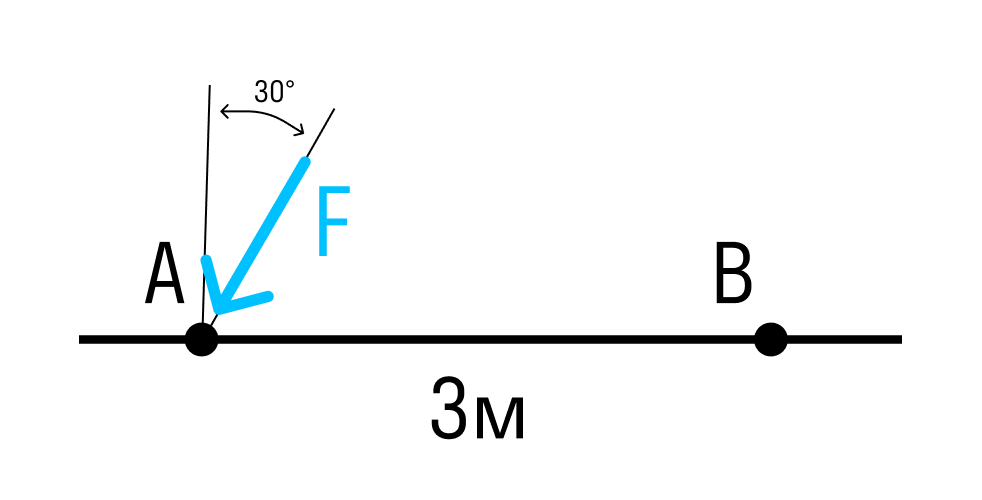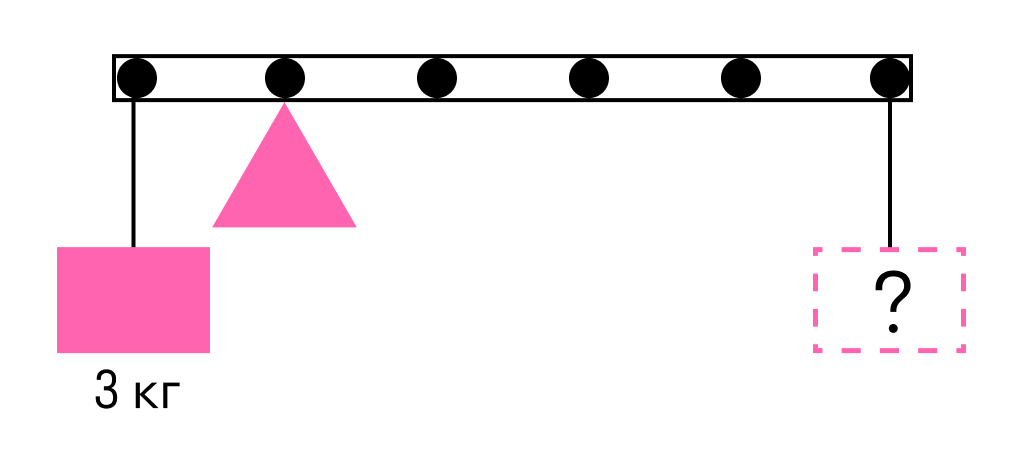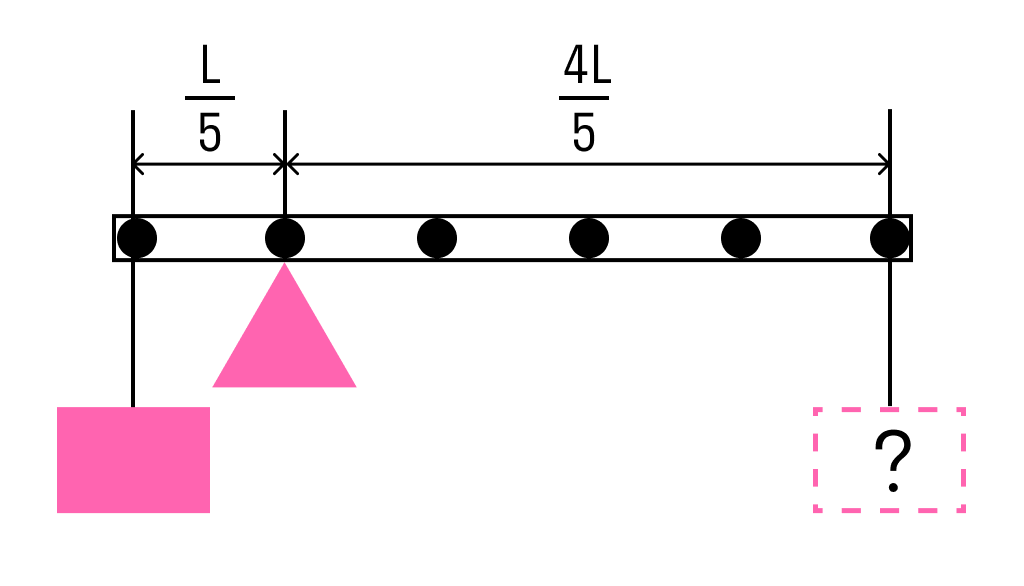какую физическую величину называют моментом силы

Момент силы

Сила: что это за величина

В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.

Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.

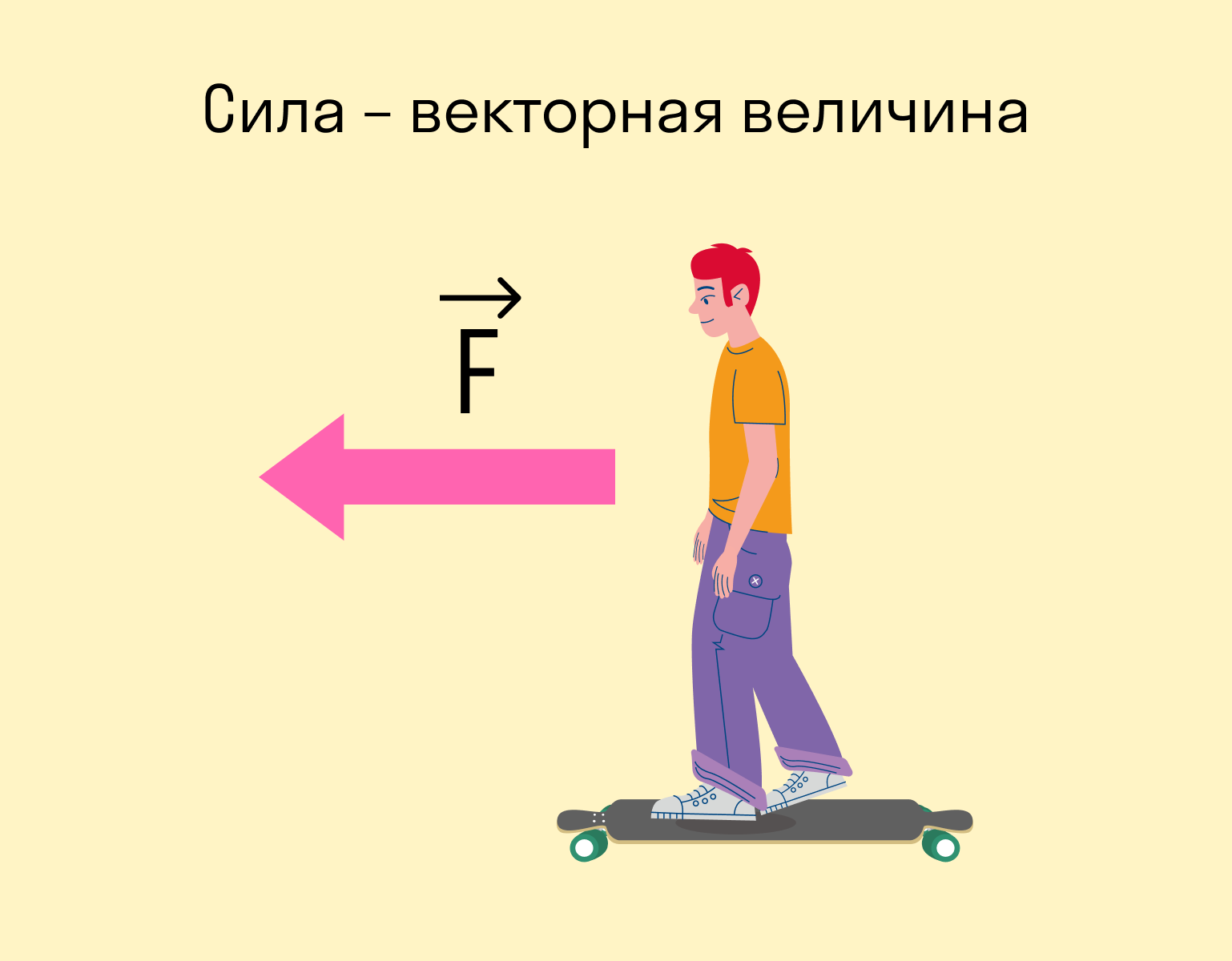
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.

Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.

Плечо силы

Для начала давайте разберемся, что такое плечо силы — оно нам сегодня очень пригодится.

Представьте человека. Совершенно обычного. Если он совершенно обычный, у него точно будут плечи — без них получится уже какой-то инопланетянин. Если мы прочертим прямую вдоль линии плеча, а потом еще одну — вдоль линии руки — мы получим две пересекающиеся прямые. Угол между такими прямыми будет равен 90 градусов, а значит эти линии перпендикулярны.

Как анатомическое плечо перпендикулярно руке, так и в физике плечо перпендикулярно, только уже линии действия силы.

То есть перпендикуляр, проведенный от точки опоры до линии действия силы —это плечо силы.

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Момент силы

При решении задач на различные силы нам обычно хватало просто сил. Сила действует всегда линейно (ну в худшем случае под углом), поэтому очень удобно пользоваться законами Ньютона, приравнивать разные силы. Это работало с материальными точками, но не будет так просто применяться к телам, у которых есть форма и размер.

Вот мы приложили силу к краю палки, но при этом не можем сказать, что на другом ее конце будут то же самое ускорение и та же самая сила. Для этого мы вводим такое понятие, как момент силы.

Момент силы — это векторное произведение силы на плечо. Для определения физического смысла можно сказать, что момент — это вращательное действие.

Момент силы

M = Fl

M — момент силы [Н*м]
F — сила [Н]
l — плечо [м]

Вернемся к примеру с дверями. Вот мы приложили силу к краю двери — туда, где самый длинный рычаг. Получаем некоторое значение момента силы.

Теперь ту же силу приложим ближе к креплению двери, там, где плечо намного короче. По формуле получим момент меньшей величины.

На себе мы это ощущаем таким образом: нам легче толкать дверь там, где момент больше. То есть, чем больше момент, тем легче идет вращение.

То же самое можно сказать про гаечный ключ. Чтобы закрутить гайку, нужно взяться за ручку дальше гайки.

В этом случае, прикладывая ту же силу, мы получаем большую величину момента за счет увеличения плеча.

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

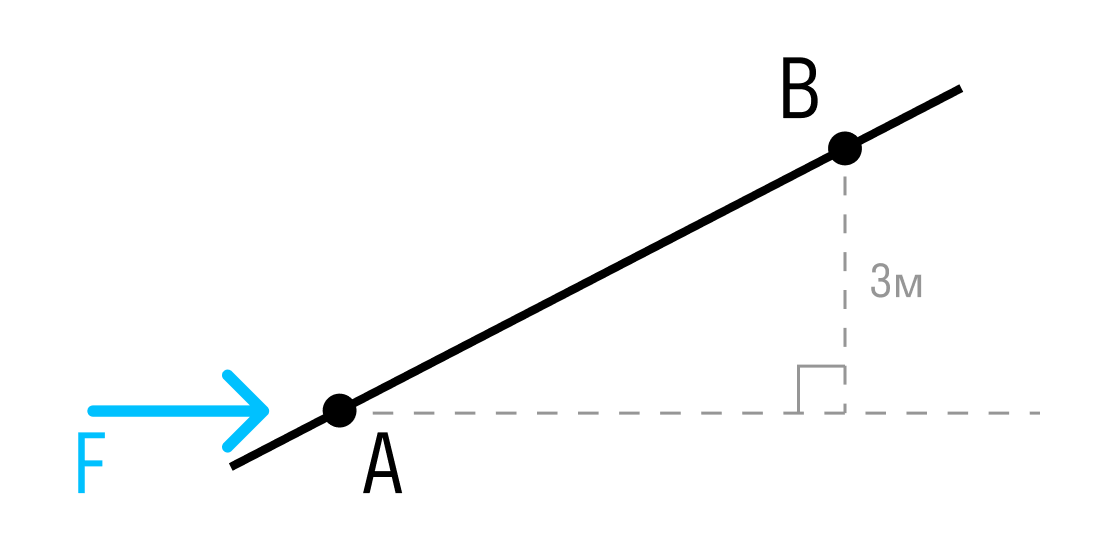
Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

Момент силы относительно точки A:

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

Момент силы относительно точки B:

Если известно расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

Момент силы относительно точки B:

Правило моментов

Вернемся к нашим баранам качелям. Мы умудряемся на них качаться, потому что существует вращательное действие — момент. Силы, с которыми мы действуем на разные стороны этих качелей могут быть разными, но вот моменты должны быть одинаковыми.

Правило моментов говорит о том, что если рычаг не вращается, то сумма моментов сил, поворачивающих рычаг против часовой стрелки, равна сумме моментов сил, поворачивающих рычаг по часовой стрелке.

Это условие выполняется относительно любой точки.

Правило моментов

M1 + M2 +. + Mn = M’1 + M’2 +. + M’n

M1 + M2 +. + Mn — сумма моментов сил, поворачивающих рычаг по часовой стрелке [Н*м]

Давайте рассмотрим этот закон на примере задач.

Задача 1

К левому концу невесомого стержня прикреплен груз массой 3 кг.

Стержень расположили на опоре, отстоящей от его левого конца на 0,2 длины стержня. Чему равна масса груза, который надо подвесить к правому концу стержня, чтобы он находился в равновесии?

Решение:

Одним из условий равновесия стержня является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно точки опоры. Момент, создаваемый левым грузом равен mgL5 он вращает стержень против часовой стрелки. Момент, создаваемый правым грузом:Mg4L5 — он вращает по часовой.

Приравнивая моменты, получаем, что для равновесия к правому концу стержня необходимо подвесить груз массой
M = m : 4 = 3 : 4 = 0,75 кг

Ответ: для равновесия к правому концу стержня необходимо подвесить груз массой 0,75 кг

Задача 2

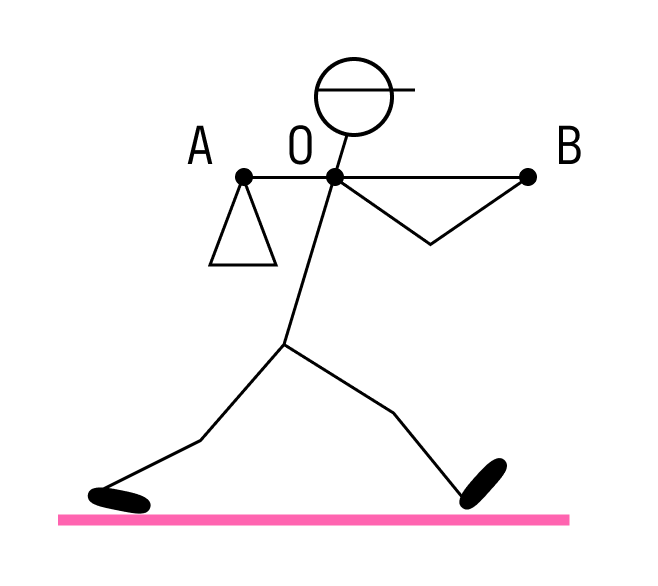
Путешественник несёт мешок с вещами на лёгкой палке. Чтобы удержать в равновесии груз весом 80 Н, он прикладывает к концу B палки вертикальную силу 30 Н. OB = 80 см. Чему равно OA?

Решение:

По правилу рычага: FB/FA=|OA|/|OB| где FA и FB — силы, приложенные соответственно к точкам A и B. Выразим длину OA:

Ответ: расстояние ОА равно 30 см

Задача 3

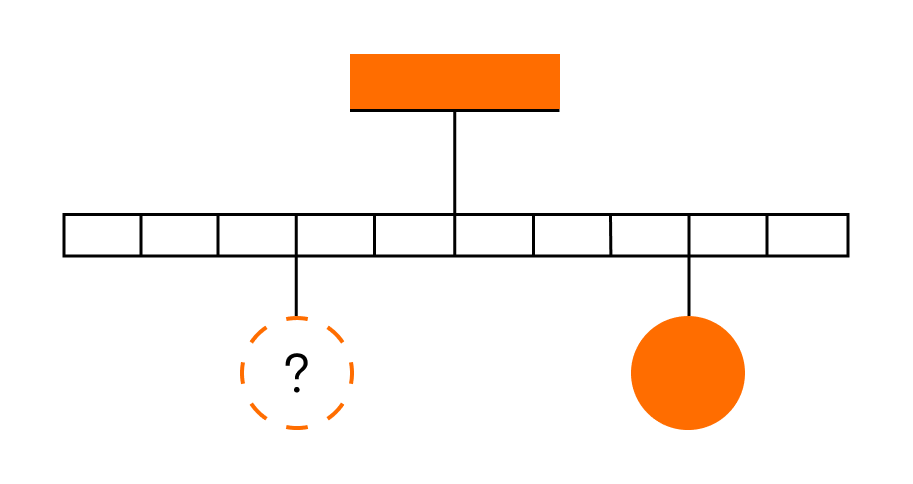
Тело массой 0,2 кг подвешено к правому плечу невесомого рычага (см. рисунок). Груз какой массы надо подвесить ко второму делению левого плеча рычага для достижения равновесия?

Решение:

По правилу рычага m1g*l1=m2g*l2

Отсюда m2=l1/l2*m1=3/2*0,2 = 0,3 кг

Ответ: Масса груза равна 0,3 кг

Задача 4

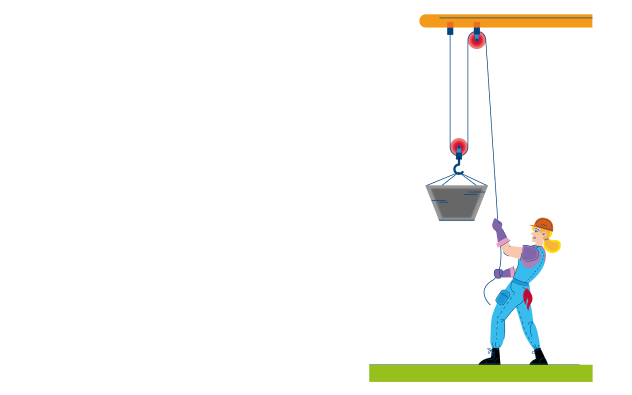
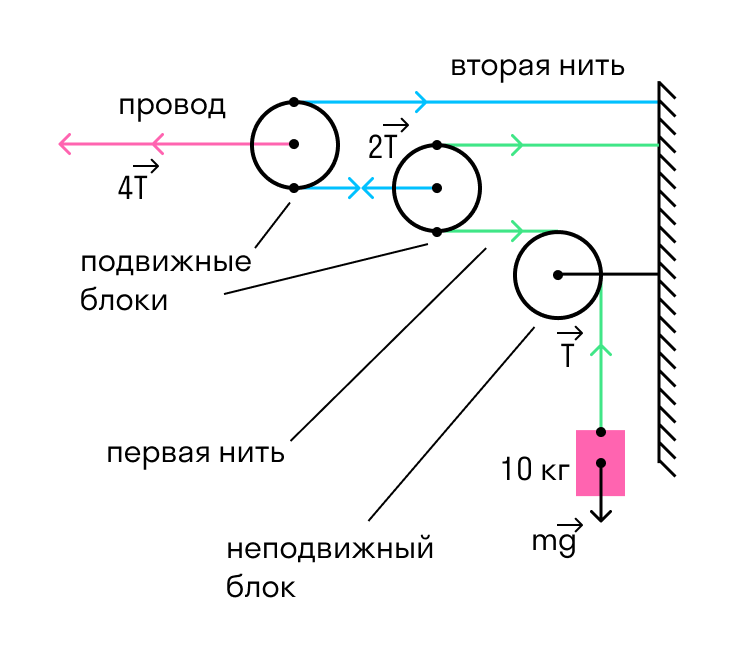
На железной дороге для натяжения проводов используется показанная на рисунке система, состоящая из легких блоков и тросов, натягиваемых тяжелым грузом. Чему равна сила натяжения провода?

Решение:

Система на рисунке состоит из трех блоков: двух подвижных и одного неподвижного. Назначение неподвижного блока заключается только в том, что он меняет направление действия силы, однако никакого выигрыша в силе при этом не возникает. Каждый подвижный блок, напротив, дает выигрыш в силе.

Определим силу, с которой натянута первая нить. Груз растягивает ее с силой:
T = mg = 10*10 = 100 Н

Рассмотрим теперь первый подвижный блок. Так как вся система статична, полная сила, действующая на этот блок, должна быть равна нулю. Первая нить тянет его направо с суммарной силой 2T, значит, натяжение второй нити тоже должно быть равно 2T (вот он — выигрыш в силе). Аналогичное рассмотрение для второго подвижного блока показывает, что натяжение провода должно быть равно

Ответ: натяжение провода равно 400 Н

Задача 5 — a.k.a самая сложная задачка

Под действием силы тяжести mg груза и силы F рычаг, представленный на рисунке, находится в равновесии. Вектор силы F перпендикулярен рычагу, груз на плоскость не давит. Расстояния между точками приложения сил и точкой опоры, а также проекции этих расстояний на вертикальную и горизонтальную оси указаны на рисунке.

Если модуль силы F равен 120 Н, то каков модуль силы тяжести, действующей на груз?

Решение:

Одним из условий равновесия рычага является то, что полный момент всех внешних сил относительно любой точки равен нулю. Рассмотрим моменты сил относительно опоры рычага. Момент, создаваемый силой F, равен F*5 м и он вращает рычаг по часовой стрелке. Момент, создаваемый грузом относительно этой точки — mg*0,8 м, он вращает против часовой. Приравнивая моменты, получаем выражение для модуля силы тяжести

Ответ: модуль силы тяжести, действующей на груз равен 750 Н

Источник

Статика. Момент силы.

Момент силы вычисляют при помощи формулы:

Плечо силы – это самое короткое расстояние от линии действия силы до оси вращения тела. На рисунке ниже изображено твердое тело, которое может вращаться вокруг оси. Ось вращения этого тела является перпендикулярной к плоскости рисунка и проходит через точку, которая обозначена как буква О. Пле­чом силы F_t здесь оказывается расстояние l, от оси вращения до линии действия силы. Определяют его таким образом. Первым шагом проводят линию действия силы, далее из т. О, через которую проходит ось вращения тела, опускают на линию действия силы перпендикуляр. Длина этого перпендикуляра оказывается плечом данной силы.

Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от плеча. Чем больше плечо, тем меньшую силу необходимо приложить, чтобы получить желаемый результат, то есть один и тот же момент силы (см. рис. выше). Именно поэтому открыть дверь, толкая ее возле петель, намного сложнее, чем берясь за ручку, а гайку отвернуть намного легче длинным, чем коротким гаечным ключом.

За единицу момента силы в СИ принимается момент силы в 1 Н, плечо которой равно 1м — ньютон-метр (Н · м).

Правило моментов.

Твердое тело, которое может вращаться вокруг неподвижной оси, находится в равновесии, если момент силы М₁ вращающей его по часовой стрелке, равняется моменту силы М₂, которая вращает его против часовой стрелки:

Момент силы принято считать положительным, если тело вращается по часовой стрелке, и от­рицательным, если — против.

Правило моментов есть следствие одной из теорем механики, которая была сформулирована французским ученым П. Вариньоном в 1687 г.

Пара сил.

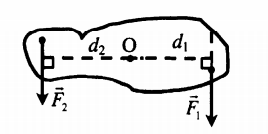
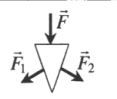
Если на тело действуют 2 равные и противоположно направленные силы, которые не лежат на одной прямой, то такое тело не находится в равновесии, так как результирующий момент этих сил относительно любой оси не равняется нулю, так как обе силы имеют моменты, направленные в одну сторону. Две такие силы, одновременно действующие на тело, называют парой сил. Если тело закреплено на оси, то под действием пары сил оно будет вращаться. Если пара сил приложена «свободному телу, то оно будет вращаться вокруг оси. проходящей через центр тяжести тела, рисунке б.

Момент пары сил одинаков относительно любой оси, перпендикулярной к плоскости пары. Суммарный момент М пары всегда равен произведению одной из сил F на расстояние l между силами, которое называется плечом пары, независимо от того, на какие отрезки l, и разделяет положение оси плечо пары:

.

Момент нескольких сил, равнодействующая которых равна нулю, будет одинаковым относи­тельно всех осей, параллельных друг другу, поэтому действие всех этих сил на тело можно заме нить действием одной пары сил с тем же моментом.

Источник

Момент силы и правило моментов

теория по физике 🧲 статика

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие

Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (E_{p min}).

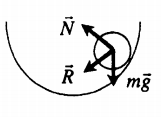
Неустойчивое равновесие

Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (E_{p max}).

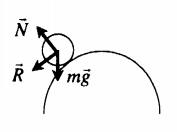
Безразличное равновесие

При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

Момент силы

Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:

M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

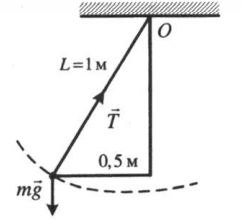
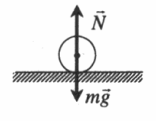
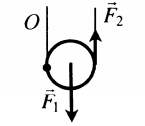
Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?

Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

Иначе правило моментов можно сформулировать так:

Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.

Условия равновесия тел

Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)

∑ → F i = 0 ; → v o = 0 и ∑ → F i = 0 ; → v o = 0

Простые механизмы

Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.

Наклонная плоскость

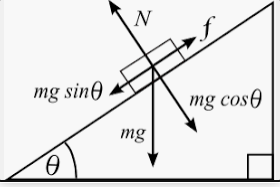
Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости:

Рычаг

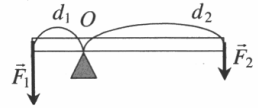
Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой:

Неподвижный блок

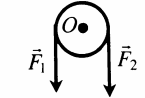
Изменяет направление действия силы. Модули и плечи сил при этом равны:

Подвижный блок

Дает выигрыш в силе в 2 раза:

Делит силу на две равные части, направление которых зависит от формы клина:

Золотое правило механики

При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии. Поэтому выигрыша в работе простые механизмы не дают.

Алгоритм решения

Решение

Известна лишь масса батона: m₁ = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:

Запишем правило моментов:

Сила тяжести равна произведению массы на ускорение свободного падения. Поэтому:

Отсюда масса рыбы равна:

pазбирался: Алиса Никитина | обсудить разбор | оценить

Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F → тр «> F _тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно.

Алгоритм решения

Решение

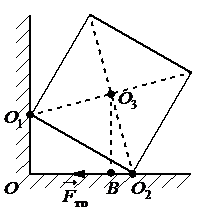
Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила. Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О₃В.

pазбирался: Алиса Никитина | обсудить разбор | оценить

Источник

Момент силы, формулы

Момент силы – это характеристика вращательного воздействия силы на объект. Момент силы рассчитывают, как векторное произведение вектора силы и радиус-вектора, опущенного от центра вращения до точки, к которой приложена сила.

При этом понятия «крутящий» и «вращающий» нельзя отождествлять, потому что технически вращающим моментом принято считать внешнее усилие, которое прикладывается к телу, а крутящий момент обозначает внутреннее усилие, появляющееся в теле при нагрузке. Данное понятие применимо при расчете сопротивления материалов.

Основные понятия

Не нашли что искали?

Просто напиши и мы поможем

Момент силы – это вращающая сила. По международной системе СИ единицей измерения момента вращающей силы есть ньютон-метр. Архимед при работе с рычагами отмечал, что моментом силы также считается момент пары сил.

На сегодняшний день момент силы измеряют при помощи оптических, индуктивных и тензометрических приборов нагрузки.

Формулы для нахождения момента силы

Данная формула позволяет определить только значение момента силы, но не его направление. Когда сила перпендикулярна вектору \(r ⃗,\) то момент рычага равняется расстоянию от центра вращения до точки действия силы, а момент силы имеет наибольшее значение:
\(\vec=\vec\vec\)

Сложно разобраться самому?

Попробуй обратиться за помощью к преподавателям

Если сила воздействует на определённом расстоянии, это значит, что она делает механическую работу. Момент силы тоже делает работу, выполняя действие через угловое расстояние.
\(P = \vec \omega\)
где \(P\) – мощность, Ватт;
\(\vec\) – момент силы, ньютон-метр;
\(ω\) – угловая скорость, радиан/секунда.

Момент нескольких сил

Если тело закрепить на оси, то под воздействием пары сил оно будет вращаться вокруг этой оси. Если же пару сил приложить к свободному телу, то его вращение будет вокруг оси, проходящей через его центр тяжести.

Если равнодействующая момента нескольких сил равняется нулю, то он будет одинаковым по отношению ко всем параллельным между собой осям. Поэтому действие на объект данных сил можно заменить воздействием одной пары сил с таким же моментом.

Источник

Что такое момент силы: определение, формула, физический смысл. Работа момента силы

Вращение вокруг оси или точки различных объектов является одним из важных видов движения в технике и в природе, который изучают в курсе физики. Динамика вращения, в отличие от динамики линейного движения, оперирует понятием момента той или иной физической величины. Данная статья посвящена вопросу, что такое момент сил.

Понятие о моменте силы

Каждый любитель велосипеда хотя бы один раз в своей жизни раскручивал рукой колесо своего «железного коня». Если описанное действие выполнять, взявшись рукой за покрышку, то раскрутить колесо гораздо легче, чем взявшись за спицы ближе к оси вращения. Это простое действие описывается в физике с помощью момента силы или вращающего момента.

Вам будет интересно: Основная образовательная программа дошкольного образования: разработка, содержание, задачи

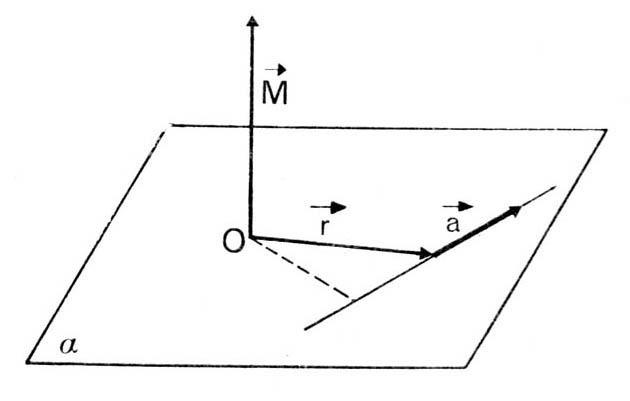
Что такое момент силы? Ответить на этот вопрос можно, если представить себе систему, которая может вращаться вокруг оси O. Если в некоторой точке P к системе приложить вектор силы F¯, тогда момент действующей силы F¯ будет равен:

То есть момент M¯ представляет собой векторную величину, равную произведению векторной силы F¯ на радиус-вектор OP¯.

Записанная формула позволяет отметить важный факт: если внешняя сила F¯ приложена под любым углом к любой точке оси вращения, то момента она не создает.

Абсолютная величина момента силы

В предыдущем пункте мы рассмотрели определение, что такое момент силы относительно оси. Теперь обратимся к рисунку ниже.

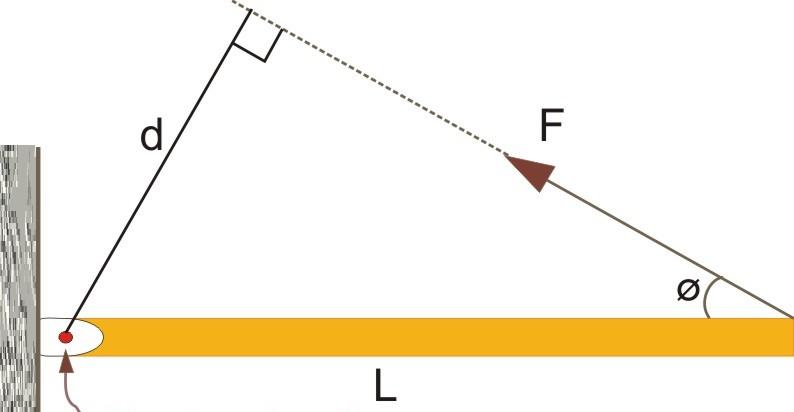
Здесь изображен некоторый стержень, имеющий длину L. С одной стороны он закреплен через шарнирное соединение на вертикальной стене. Другой конец стержня является свободным. На этот конец оказывает действие сила F¯. Также известен угол между стержнем и вектором силы. Он равен φ.

Вращающий момент определяется через векторное произведение. Модуль такого произведения равен произведению абсолютных значений векторов на синус угла между ними. Применяя тригонометрические формулы, приходим к следующему равенству:

Обращаясь снова к рисунку выше, можно это равенство переписать в следующей форме:

M = d*F, где d = L*sin(φ).

Величина d, которая равна расстоянию от вектора силы до оси вращения, получила название рычага силы. Чем больше значение d, тем больший момент создаст сила F.

Направление момента силы и его знак

Изучение вопроса, что такое момент силы, не может быть полным, если не рассмотреть его векторную природу. Вспоминая свойства векторного произведения, можно с уверенностью сказать, что момент силы будет перпендикулярен плоскости, построенной на векторах-множителях.

Конкретное направление M¯ определяется однозначно, если применить так называемое правило буравчика. Звучит оно просто: вращая буравчик по направлению кругового движения системы, поступательным движением буравчика определяется направление момента силы.

Если смотреть на вращающуюся систему вдоль ее оси, то вектор момента силы, приложенный к точке, может быть направлен как на читателя, так и от него. В связи с этим при количественных расчетах используют понятие о положительном или об отрицательном моменте. В физике принято положительным считать тот момент силы, который приводит к вращению системы против хода часовой стрелки.

В чем смысл величины M¯?

Разную возможность совершения вращения или поворота легко понять, если вспомнить, что дверь открывается легче, если ее толкнуть подальше от дверных петель, то есть в области ручки. Еще один пример: любой более-менее тяжелый предмет легче удержать, если прижать руку к телу, чем держать его на вытянутой руке. Наконец, открутить гайку проще, если воспользоваться длинным ключом. В названных примерах момент силы изменяется за счет уменьшения или увеличения рычага силы.

Здесь уместно привести аналогию философского характера, взяв за пример книгу Экхарта Толле «Сила момента Сейчас». Книга относится к психологическому жанру и учит жить без стресса в данный момент своей жизни. Только текущее мгновение имеет смысл, только во время него совершаются все действия. Учитывая названную идею книги «Сила момента Сейчас» можно сказать, что вращающий момент в физике осуществляет ускорение или замедление вращения в текущий момент времени. Поэтому главное уравнение моментов имеет следующий вид:

Важность понятия о моменте силы для статики

Многие знакомы с задачами на рычаги разного рода. Практически во всех этих задачах статики требуется найти условия равновесия системы. Для нахождения этих условий проще всего воспользоваться концепцией момента силы.

Если система не движется и находится в состоянии равновесия, то сумма всех моментов сил относительно оси, точки или выбранной опоры должна быть равна нулю, то есть:

Напомним, что абсолютные значения моментов Mi в равенство выше нужно подставлять с учетом их знака. Сила реакции опоры, которая рассматривается в качестве оси вращения, вращающего момента не создает. Ниже приводится видео, которое поясняет тему этого пункта статьи.

Момент силы и его работа

Источник