Как называют цилиндр в геометрии
Цилиндр (геометрия)
Бесконечное тело, ограниченное замкнутой бесконечной цилиндрической поверхностью, называется бесконечным цилиндром, ограниченное замкнутым цилиндрическим лучом и его основанием, называется открытым цилиндром. Основание и образующие цилиндрического луча называют соответственно основанием и образующими открытого цилиндра.
Конечное тело, ограниченное замкнутой конечной цилиндрической поверхностью и двумя выделившими её сечениями, называется конечным цилиндром, или собственно цилиндром. Сечения называются основаниями цилиндра. По определению конечной цилиндрической поверхности, основания цилиндра равны.
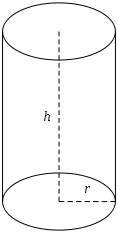
Очевидно, образующие боковой поверхности цилиндра — равные по длине (называемой высотой цилиндра) отрезки, лежащие на параллельных прямых, а концами лежащие на основаниях цилиндра. К математическим курьёзам относят определение любой конечной трёхмерной поверхности без самопересечений как цилиндра нулевой высоты (данную поверхность считают одновременно обоими основаниями конечного цилиндра). Основания цилиндра качественно влияют на цилиндр.
Если основания цилиндра плоские (и, следовательно, содержащие их плоскости параллельны), то цилиндр называют стоящим на плоскости. Если основания стоящего на плоскости цилиндра перпендикулярны образующей, то цилиндр называется прямым.
В частности, если основание стоящего на плоскости цилиндра — круг, то говорят о круговом (круглом) цилиндре; если эллипс — то эллиптическом.
Объём конечного цилиндра равен интегралу площади основания по образующей. В частности, объём прямого кругового цилиндра равен
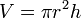
(где 
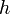
Площадь боковой поверхности цилиндра считается по следующей формуле:
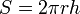
Площадь полной поверхности цилиндра складывается из площади боковой поверхности и площади оснований. Для прямого кругового цилиндра:
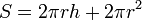
Что такое цилиндр: определение, элементы, виды, варианты сечения
В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения одной из самых распространенных трехмерных геометрических фигур – цилиндра. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.
Определение цилиндра
Далее мы подробно остановимся на прямом круговом цилиндре как самой популярной разновидности фигуры. Другие ее виды будут перечислены в последнем разделе данной публикации.
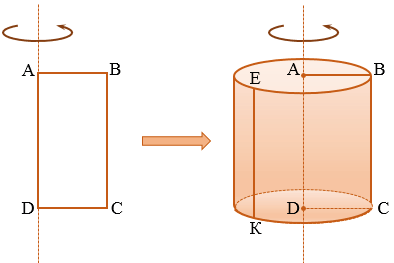
Прямой круговой цилиндр – это геометрическая фигура в пространстве, полученная путем вращения прямоугольника вокруг своей стороны или оси симметрии. Поэтому такой цилиндр иногда называют цилиндром вращения.
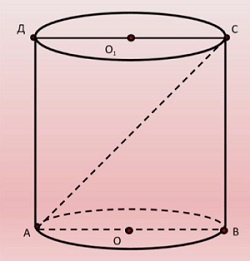
Цилиндр на рисунке выше получен в результате вращения прямоугольного треугольника ABCD вокруг оси O1O2 на 180° или прямоугольников ABO2O1/O1O2CD вокруг стороны O1O2 на 360°.
Основные элементы цилиндра
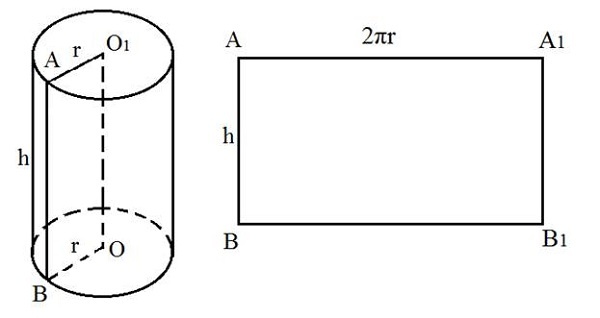
Развёртка цилиндра – боковая (цилиндрическая) поверхность фигуры, развернутая в плоскость; является прямоугольником.
Примечание: формулы для нахождения площади поверхности и объема цилиндра представлены в отдельных публикациях.
Определение цилиндра: его основание и высота, разновидности
Разбираемся в особенностях трехмерного геометрического тела под названием цилиндр. Смотрим виды цилиндров, его свойства, какие бывают развертки, а также даем определения составным частям этой фигуры.
Что такое цилиндр в геометрии
Цилиндр — это трехмерное геометрическое тело, которое ограничено цилиндрической поверхностью и двумя параллельными плоскостями.
Цилиндрическая поверхность — это поверхность, которая образуется за счет движения в пространстве прямой (образующей) параллельно самой себе, пересекающей данную линию (направляющую).
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Основания — это одинаковые круги, которые ограничивают цилиндр и находятся параллельно друг другу.
Образующая — отрезок, который соединяет точки окружностей оснований цилиндра и перпендикулярный плоскостям этих оснований. Она равна высоте цилиндра или расстоянию от одного его основания до другого.
Виды цилиндров
Классификация цилиндров может быть разной в зависимости от тех или иных параметров:
У прямого цилиндра образующие строго перпендикулярны основаниям фигуры.
Помимо кругов, в основаниях фигуры могут быть еще и эллипсы или другие замкнутые фигуры. Однако, кроме замкнутых форм, основании цилиндру может служить и парабола, и гипербола, и любая друга открытая функция. Такой цилиндр будет называться развернутым.
Как найти высоту цилиндра
Рассмотрим варианты нахождения высоты фигуры, а также длины ее образующей (которая равна этой высоте).
Через эту формулу можем выразить высоту:
Таким образом мы можем узнать H данного геометрического тела, если нам известен его объем и радиус. Если же вместо радиуса мы знаем диаметр, формула расчета будет выглядеть так:
В случае, когда нам известен диаметр и площадь фигуры, мы так же можем найти высоту. Следует обратить внимание, что в зависимости от того, будет ли известна площадь боковой или полной поверхности, формула будет меняться.
Для расчета S боковой поверхности (часть, ограниченная цилиндрической поверхностью) цилиндра мы используем формулу:
выражаем H и получаем:
Если известна S полной поверхности (включает в себя площадь оснований фигуры), используем формулу:
\(S=2\pi R(H+R)=2\pi R\times H+2\pi R^2\)
выражаем H и получаем:
Таким образом, получается прямоугольный треугольник САВ. А так как высота равна образующей, мы можем вычислить ее по теореме Пифагора:
Развертка
Как уже было упомянуто выше, всего существует две площади поверхности цилиндра: боковой поверхности и полной поверхности. У каждой из них также есть и своя развертка. Разберемся, как они выглядят.
Развертка боковой поверхности
Легче всего представить себе развертку боковой поверхности цилиндра, посмотрев на этикетку пластиковой бутылки. Когда вы ее отклеиваете, то видите прямоугольник. То же самое и с цилиндрическим геометрическим телом: развёрткой его боковой поверхности является прямоугольник. Его длина соответствует длине окружности, лежащей в основании, а ширина — высоте самой трехмерной фигуры.
Развертка полной поверхности
Если развернуть полную поверхность цилиндра, получится примерно то же самое, только с двумя дополнительными элементами в виде окружностей оснований. Выглядит это так:
Геометрические тела. Цилиндр.
 |  |
Цилиндрическая поверхность образуется посредством движения прямой параллельно самой себе. Точка прямой, которая выделена, перемещается вдоль заданной плоской кривой – направляющей. Эта прямая называется образующей цилиндрической поверхности.
Прямой цилиндр – это такой цилиндр, в котором образующие перпендикулярны основанию. Если образующие цилиндра не перпендикулярны основанию, то это будет наклонный цилиндр.
Круговой цилиндр – цилиндр, основанием которого является круг.
Круглый цилиндр – такой цилиндр, который одновременно и прямой, и круговой.
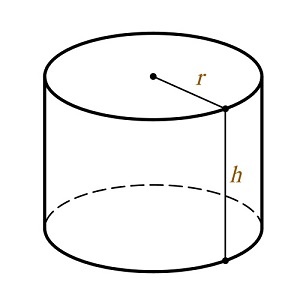
Прямой круговой цилиндр определяется радиусом основания R и образующей L, которая равна высоте цилиндра H.
Призма – это частный случай цилиндра.
Формулы нахождения элементов цилиндра.
Площадь боковой поверхности прямого кругового цилиндра:
Площадь полной поверхности прямого кругового цилиндра:
Объем прямого кругового цилиндра:
Прямой круговой цилиндр со скошенным основанием либо кратко скошенный цилиндр определяют с помощью радиуса основания R, минимальной высоты h1 и максимальной высоты h2.
Площадь боковой поверхности скошенного цилиндра:
Площадь оснований скошенного цилиндра:
Площадь полной поверхности скошенного цилиндра:
Объем скошенного цилиндра:
Цилиндр
Тела вращения – это объемные тела, которые возникают при вращении некой плоской фигуры, которая ограничена кривой и крутится вокруг оси, лежащей в той же плоскости. К телам вращения относятся цилиндр, конус и шар.
Возьмем прямоугольник АВСD. Будем вращать этот прямоугольник против часовой стрелки вокруг стороны АD.
Определение
Объем цилиндра
| Объем цилиндра равен произведению площади основания на высоту. |
Доказательство:
Дано: цилиндр с площадью основания S, высотой h и объемом V.
Доказать: V = Sh.
Доказательство:
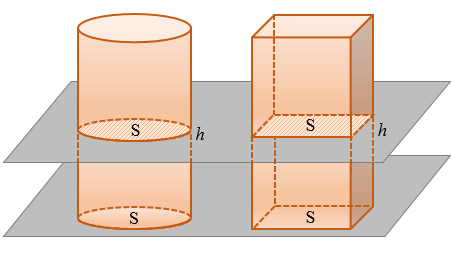
Воспользуемся принципом Кавальери. Рассмотрим цилиндр и призму с площадями оснований, равными S, и высотами, равными h, «стоящие» на одной плоскости.
Площадь боковой поверхности цилиндра
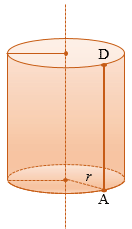
Рассмотрим цилиндр с радиусом r и высотой h.
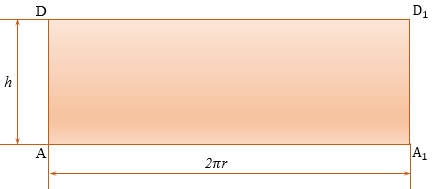
Представим, что его боковую поверхность разрезали по одной из его образующих АD и развернули так, что получился прямоугольник АDА1D1, стороны АD и А1D1 которого являются двумя краями разреза боковой поверхности цилиндра. Этот прямоугольник называется разверткой боковой поверхности цилиндра.
Сторона АА1 прямоугольника АDА1D1 равна длине окружности основания, а сторона АD равна высоте цилиндра, т.е. АА1 = 2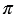
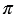
Площадь Sбок боковой поверхности цилиндра равна площади ее развертки, т.е. Sбок = 2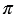 rh. rh. |
Поделись с друзьями в социальных сетях: