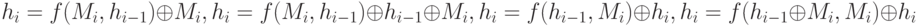Как называется значение хеш функции
Хэш-алгоритмы
О себе
Студент кафедры информационной безопасности.
О хэшировании
В настоящее время практически ни одно приложение криптографии не обходится без использования хэширования.
Хэш-функции – это функции, предназначенные для «сжатия» произвольного сообщения или набора данных, записанных, как правило, в двоичном алфавите, в некоторую битовую комбинацию фиксированной длины, называемую сверткой. Хэш-функции имеют разнообразные применения при проведении статистических экспериментов, при тестировании логических устройств, при построении алгоритмов быстрого поиска и проверки целостности записей в базах данных. Основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента.
Криптографической хеш-функцией называется всякая хеш-функция, являющаяся криптостойкой, то есть удовлетворяющая ряду требований специфичных для криптографических приложений. В криптографии хэш-функции применяются для решения следующих задач:
— построения систем контроля целостности данных при их передаче или хранении,
— аутентификация источника данных.
Как правило хэш-функции строят на основе так называемых одношаговых сжимающих функций y = f(x1, x2) двух переменных, где x1, x2 и y — двоичные векторы длины m, n и n соответственно, причем n — длина свертки, а m — длина блока сообщения.
Для получения значения h(M) сообщение сначала разбивается на блоки длины m (при этом, если длина сообщения не кратна m то последний блок неким специальным образом дополняется до полного), а затем к полученным блокам M1, M2. MN применяют следующую последовательную процедуру вычисления свертки:
Здесь v — некоторая константа, часто ее называют инициализирующим вектором. Она выбирается
из различных соображений и может представлять собой секретную константу или набор случайных данных (выборку даты и времени, например).
При таком подходе свойства хэш-функции полностью определяются свойствами одношаговой сжимающей функции.
Выделяют два важных вида криптографических хэш-функций — ключевые и бесключевые. Ключевые хэш-функции называют кодами аутентификации сообщений. Они дают возможность без дополнительных средств гарантировать как правильность источника данных, так и целостность данных в системах с доверяющими друг другу пользователями.
Бесключевые хэш-функции называются кодами обнаружения ошибок. Они дают возможность с помощью дополнительных средств (шифрования, например) гарантировать целостность данных. Эти хэш-функции могут применяться в системах как с доверяющими, так и не доверяющими друг другу пользователями.
О статистических свойствах и требованиях
Как я уже говорил основным требованием к хэш-функциям является равномерность распределения их значений при случайном выборе значений аргумента. Для криптографических хеш-функций также важно, чтобы при малейшем изменении аргумента значение функции сильно изменялось. Это называется лавинным эффектом.
К ключевым функциям хэширования предъявляются следующие требования:
— невозможность фабрикации,
— невозможность модификации.
Первое требование означает высокую сложность подбора сообщения с правильным значением свертки. Второе — высокую сложность подбора для заданного сообщения с известным значением свертки другого сообщения с правильным значением свертки.
К бесключевым функциям предъявляют требования:
— однонаправленность,
— устойчивость к коллизиям,
— устойчивость к нахождению второго прообраза.
Под однонаправленностью понимают высокую сложность нахождения сообщения по заданному значению свертки. Следует заметить что на данный момент нет используемых хэш-функций с доказанной однонаправленностью.
Под устойчивостью к коллизиям понимают сложность нахождения пары сообщений с одинаковыми значениями свертки. Обычно именно нахождение способа построения коллизий криптоаналитиками служит первым сигналом устаревания алгоритма и необходимости его скорой замены.
Под устойчивостью к нахождению второго прообраза понимают сложность нахождения второго сообщения с тем же значением свертки для заданного сообщения с известным значением свертки.
Это была теоретическая часть, которая пригодится нам в дальнейшем…
О популярных хэш-алгоритмах
Алгоритмы CRC16/32 — контрольная сумма (не криптографическое преобразование).
Алгоритмы MD2/4/5/6. Являются творением Рона Райвеста, одного из авторов алгоритма RSA.
Алгоритм MD5 имел некогда большую популярность, но первые предпосылки взлома появились еще в конце девяностых, и сейчас его популярность стремительно падает.
Алгоритм MD6 — очень интересный с конструктивной точки зрения алгоритм. Он выдвигался на конкурс SHA-3, но, к сожалению, авторы не успели довести его до кондиции, и в списке кандидатов, прошедших во второй раунд этот алгоритм отсутствует.
Алгоритмы линейки SHA Широко распространенные сейчас алгоритмы. Идет активный переход от SHA-1 к стандартам версии SHA-2. SHA-2 — собирательное название алгоритмов SHA224, SHA256, SHA384 и SHA512. SHA224 и SHA384 являются по сути аналогами SHA256 и SHA512 соответственно, только после расчета свертки часть информации в ней отбрасывается. Использовать их стоит лишь для обеспечения совместимости с оборудованием старых моделей.
Российский стандарт — ГОСТ 34.11-94.
Криптографические хеш-функции
Цель лекции: познакомиться с понятием «хеш- функция «, а также с принципами работы таких функций.
Понятие хеш-функции
где М – исходное сообщение, называемое иногда прообразом, а h – результат, называемый значением хеш-функции (а также хеш-кодом или дайджестом сообщения (от англ. message digest )).
Хеш-функции широко применяются в современной криптографии.
Например, пусть исходное сообщение, переведенное в цифровой вид, было следующим (в шестнадцатеричном формате):
Переведем сообщение в двоичный вид, запишем байты друг под другом и сложим биты в каждом столбике по модулю 2:
Результат ( 0110 0101(2) или 65(16) ) и будет значением хеш-функции.
Однако такую хеш-функцию нельзя использовать для криптографических целей, например для формирования электронной подписи, так как достаточно легко изменить содержание подписанного сообщения, не меняя значения контрольной суммы.
Поэтому рассмотренная хеш- функция не годится для криптографических применений. В криптографии хеш- функция считается хорошей, если трудно создать два прообраза с одинаковым значением хеш-функции, а также, если у выхода функции нет явной зависимости от входа.
Сформулируем основные требования, предъявляемые к криптографическим хеш-функциям:
Создать хеш-функцию, которая удовлетворяет всем перечисленным требованиям – задача непростая. Необходимо также помнить, что на вход функции поступают данные произвольного размера, а хеш-результат не должен получаться одинаковым для данных разного размера.
В настоящее время на практике в качестве хеш-функций применяются функции, обрабатывающие входное сообщение блок за блоком и вычисляющие хеш- значение hi для каждого блока Mi входного сообщения по зависимостям вида
где hi-1 – результат, полученный при вычислении хеш-функции для предыдущего блока входных данных.
В результате выход хеш-функции hn является функцией от всех n блоков входного сообщения.
Использование блочных алгоритмов шифрования для формирования хеш-функции
Возможен также другой способ использования блочного шифра в режиме простой замены: элементы сообщения шифруются хеш-значениями, полученными на предыдущем этапе:
На самом деле возможны еще несколько схем использования блочного шифра для формирования хеш-функции. Пусть Мi – блок исходного сообщения, hi – значение хеш-функции на i-том этапе, f – блочный алгоритм шифрования, используемый в режиме простой замены, 
Во всех этих схемах длина формируемого хеш-значения равна длине блока при шифровании. Все эти, а также некоторые другие схемы использования блочного алгоритма шифрования для вычисления хеш-значений могут применяться на практике.
Хеш-функция, что это такое?
Приветствую уважаемого читателя!
Сегодня я хотел бы рассказать о том, что из себя представляет хеш-функция, коснуться её основных свойств, привести примеры использования и в общих чертах разобрать современный алгоритм хеширования SHA-3, который был опубликован в качестве Федерального Стандарта Обработки Информации США в 2015 году.
Общие сведения
Результат, производимый хеш-функцией, называется «хеш-суммой» или же просто «хешем», а входные данные часто называют «сообщением».
Для идеальной хеш-функции выполняются следующие условия:
а) хеш-функция является детерминированной, то есть одно и то же сообщение приводит к одному и тому же хеш-значению
b) значение хеш-функции быстро вычисляется для любого сообщения
c) невозможно найти сообщение, которое дает заданное хеш-значение
d) невозможно найти два разных сообщения с одинаковым хеш-значением
e) небольшое изменение в сообщении изменяет хеш настолько сильно, что новое и старое значения кажутся некоррелирующими
Давайте сразу рассмотрим пример воздействия хеш-функции SHA3-256.
Число 256 в названии алгоритма означает, что на выходе мы получим строку фиксированной длины 256 бит независимо от того, какие данные поступят на вход.
На рисунке ниже видно, что на выходе функции мы имеем 64 цифры шестнадцатеричной системы счисления. Переводя это в двоичную систему, получаем желанные 256 бит.
Любой заинтересованный читатель задаст себе вопрос: «А что будет, если на вход подать данные, бинарный код которых во много раз превосходит 256 бит?»
Надеюсь, теперь нет сомнений в том, что это очень внушительное число!
Поэтому ничего не мешает нам сопоставлять длинному входному массиву данных массив фиксированной длины.
Свойства
Криптографическая хеш-функция должна уметь противостоять всем известным типам криптоаналитических атак.
В теоретической криптографии уровень безопасности хеш-функции определяется с использованием следующих свойств:
Pre-image resistance
Имея заданное значение h, должно быть сложно найти любое сообщение m такое, что
Second pre-image resistance
Имея заданное входное значение , должно быть сложно найти другое входное значение
такое, что
Collision resistance
Должно быть сложно найти два различных сообщения и
таких, что
Такая пара сообщений и
называется коллизией хеш-функции
Давайте чуть более подробно поговорим о каждом из перечисленных свойств.
Collision resistance. Как уже упоминалось ранее, коллизия происходит, когда разные входные данные производят одинаковый хеш. Таким образом, хеш-функция считается устойчивой к коллизиям до того момента, пока не будет обнаружена пара сообщений, дающая одинаковый выход. Стоит отметить, что коллизии всегда будут существовать для любой хеш-функции по той причине, что возможные входы бесконечны, а количество выходов конечно. Хеш-функция считается устойчивой к коллизиям, когда вероятность обнаружения коллизии настолько мала, что для этого потребуются миллионы лет вычислений.
Несмотря на то, что хеш-функций без коллизий не существует, некоторые из них достаточно надежны и считаются устойчивыми к коллизиям.
Pre-image resistance. Это свойство называют сопротивлением прообразу. Хеш-функция считается защищенной от нахождения прообраза, если существует очень низкая вероятность того, что злоумышленник найдет сообщение, которое сгенерировало заданный хеш. Это свойство является важным для защиты данных, поскольку хеш сообщения может доказать его подлинность без необходимости раскрытия информации. Далее будет приведён простой пример и вы поймете смысл предыдущего предложения.
Second pre-image resistance. Это свойство называют сопротивлением второму прообразу. Для упрощения можно сказать, что это свойство находится где-то посередине между двумя предыдущими. Атака по нахождению второго прообраза происходит, когда злоумышленник находит определенный вход, который генерирует тот же хеш, что и другой вход, который ему уже известен. Другими словами, злоумышленник, зная, что пытается найти
такое, что
Отсюда становится ясно, что атака по нахождению второго прообраза включает в себя поиск коллизии. Поэтому любая хеш-функция, устойчивая к коллизиям, также устойчива к атакам по поиску второго прообраза.
Неформально все эти свойства означают, что злоумышленник не сможет заменить или изменить входные данные, не меняя их хеша.
Таким образом, если два сообщения имеют одинаковый хеш, то можно быть уверенным, что они одинаковые.
В частности, хеш-функция должна вести себя как можно более похоже на случайную функцию, оставаясь при этом детерминированной и эффективно вычислимой.
Применение хеш-функций
Рассмотрим несколько достаточно простых примеров применения хеш-функций:
• Проверка целостности сообщений и файлов
Сравнивая хеш-значения сообщений, вычисленные до и после передачи, можно определить, были ли внесены какие-либо изменения в сообщение или файл.
• Верификация пароля
Проверка пароля обычно использует криптографические хеши. Хранение всех паролей пользователей в виде открытого текста может привести к массовому нарушению безопасности, если файл паролей будет скомпрометирован. Одним из способов уменьшения этой опасности является хранение в базе данных не самих паролей, а их хешей. При выполнении хеширования исходные пароли не могут быть восстановлены из сохраненных хеш-значений, поэтому если вы забыли свой пароль вам предложат сбросить его и придумать новый.
• Цифровая подпись
Подписываемые документы имеют различный объем, поэтому зачастую в схемах ЭП подпись ставится не на сам документ, а на его хеш. Вычисление хеша позволяет выявить малейшие изменения в документе при проверке подписи. Хеширование не входит в состав алгоритма ЭП, поэтому в схеме может быть применена любая надежная хеш-функция.
Предлагаю также рассмотреть следующий бытовой пример:
Алиса ставит перед Бобом сложную математическую задачу и утверждает, что она ее решила. Боб хотел бы попробовать решить задачу сам, но все же хотел бы быть уверенным, что Алиса не блефует. Поэтому Алиса записывает свое решение, вычисляет его хеш и сообщает Бобу (сохраняя решение в секрете). Затем, когда Боб сам придумает решение, Алиса может доказать, что она получила решение раньше Боба. Для этого ей нужно попросить Боба хешировать его решение и проверить, соответствует ли оно хеш-значению, которое она предоставила ему раньше.
Теперь давайте поговорим о SHA-3.
Национальный институт стандартов и технологий (NIST) в течение 2007—2012 провёл конкурс на новую криптографическую хеш-функцию, предназначенную для замены SHA-1 и SHA-2.
Организаторами были опубликованы некоторые критерии, на которых основывался выбор финалистов:
Способность противостоять атакам злоумышленников
• Производительность и стоимость
Вычислительная эффективность алгоритма и требования к оперативной памяти для программных реализаций, а также количество элементов для аппаратных реализаций
• Гибкость и простота дизайна
Гибкость в эффективной работе на самых разных платформах, гибкость в использовании параллелизма или расширений ISA для достижения более высокой производительности
В финальный тур попали всего 5 алгоритмов:
Победителем и новым SHA-3 стал алгоритм Keccak.
Давайте рассмотрим Keccak более подробно.
Keccak
Хеш-функции семейства Keccak построены на основе конструкции криптографической губки, в которой данные сначала «впитываются» в губку, а затем результат Z «отжимается» из губки.
Любая губчатая функция Keccak использует одну из семи перестановок которая обозначается
, где
перестановки представляют собой итерационные конструкции, состоящие из последовательности почти одинаковых раундов. Число раундов
зависит от ширины перестановки и задаётся как
где
В качестве стандарта SHA-3 была выбрана перестановка Keccak-f[1600], для неё количество раундов
Далее будем рассматривать
Давайте сразу введем понятие строки состояния, которая играет важную роль в алгоритме.
Строка состояния представляет собой строку длины 1600 бит, которая делится на и
части, которые называются скоростью и ёмкостью состояния соотвественно.
Соотношение деления зависит от конкретного алгоритма семейства, например, для SHA3-256
В SHA-3 строка состояния S представлена в виде массива слов длины
бит, всего
бит. В Keccak также могут использоваться слова длины
, равные меньшим степеням 2.
Алгоритм получения хеш-функции можно разделить на несколько этапов:
• С помощью функции дополнения исходное сообщение M дополняется до строки P длины кратной r
• Строка P делится на n блоков длины
• «Впитывание»: каждый блок дополняется нулями до строки длиной
бит (b = r+c) и суммируется по модулю 2 со строкой состояния
, далее результат суммирования подаётся в функцию перестановки
и получается новая строка состояния
, которая опять суммируется по модулю 2 с блоком
и дальше опять подаётся в функцию перестановки
. Перед началом работы криптографической губки все элементы
равны 0.
• «Отжимание»: пока длина результата меньше чем
, где
— количество бит в выходном массиве хеш-функции,
первых бит строки состояния
добавляется к результату
. После каждой такой операции к строке состояния применяется функция перестановок
и данные продолжают «отжиматься» дальше, пока не будет достигнуто значение длины выходных данных
.
Все сразу станет понятно, когда вы посмотрите на картинку ниже:
Функция дополнения
Первый единичный бит в функции дополнения нужен, чтобы результаты хеш-функции от сообщений, отличающихся несколькими нулевыми битами в конце, были различны.
Функция перестановок
Базовая функция перестановки состоит из раундов по пять шагов:
Шаг
Шаг
Шаг
Шаг
Шаг
Тета, Ро, Пи, Хи, Йота
Далее будем использовать следующие обозначения:
Так как состояние имеет форму массива
, то мы можем обозначить каждый бит состояния как
Обозначим результат преобразования состояния функцией перестановки
Также обозначим функцию, которая выполняет следующее соответствие:
— обычная функция трансляции, которая сопоставляет биту
бит
,
где — длина слова (64 бит в нашем случае)
Я хочу вкратце описать каждый шаг функции перестановок, не вдаваясь в математические свойства каждого.
Шаг
Эффект отображения можно описать следующим образом: оно добавляет к каждому биту
побитовую сумму двух столбцов
и
Схематическое представление функции:
Шаг
Отображение направлено на трансляции внутри слов (вдоль оси z).
Проще всего его описать псевдокодом и схематическим рисунком:

Шаг
Шаг представляется псевдокодом и схематическим рисунком:

Шаг
Шаг является единственный нелинейным преобразованием в
Псевдокод и схематическое представление:

Шаг
Отображение состоит из сложения с раундовыми константами и направлено на нарушение симметрии. Без него все раунды
были бы эквивалентными, что делало бы его подверженным атакам, использующим симметрию. По мере увеличения
раундовые константы добавляют все больше и больше асимметрии.
Ниже приведена таблица раундовых констант для
бит
Все шаги можно объединить вместе и тогда мы получим следующее:

Где константы являются циклическими сдвигами и задаются таблицей:
Итоги
В данной статье я постарался объяснить, что такое хеш-функция и зачем она нужна
Также в общих чертах мной был разобран принцип работы алгоритма SHA-3 Keccak, который является последним стандартизированным алгоритмом семейства Secure Hash Algorithm
Надеюсь, все было понятно и интересно
Всем спасибо за внимание!