Как называется элементарная единица информации
Как называется элементарная единица информации
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
Байт – основная единица измерения количества информации.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:
I – количество информации,
N – количество возможных событий,
Pi – вероятность i-го события.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события (N=4).
По формуле Хартли имеем: 4=2 i . Так как 2 2 =2 i , то i=2. Значит, это сообщение содержит 2 бита информации.
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log2 N=log2 32=5 битов (2 5 =32).
Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log2101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log2128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p1=1/2, p2=1/4, p3=1/8, p4=1/8.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Так как каждый символ кодируется одним байтом, нам только нужно подсчитать количество символов, но при этом не забываем считать знаки препинания и пробелы. Всего получаем 30 символов. А это означает, что информационный объем данного сообщения составляет 30 байтов или 30 * 8 = 240 битов.
Единицы измерения информации
Единицы измерения информации служат для измерения объёма информации — величины, исчисляемой логарифмически. [1] Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество информации — складывается. Не важно, идёт речь о случайных величинах в математике, регистрах цифровой памяти в технике или в квантовых системах в физике.
Чаще всего измерение информации касается объёма компьютерной памяти и объёма данных, передаваемых по цифровым каналам связи.
Содержание
Первичные единицы
Объёмы информации можно представлять как логарифм [2] количества состояний.
Наименьшее целое число, логарифм которого положителен — 2. Соответствующая ему единица — бит — является основой исчисления информации в цифровой технике.
Единица, соответствующая числу 3 (трит) равна 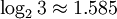
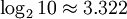
Такая единица как нат (nat, е-бит), соответствующая натуральному логарифму применяется в вычислительной технике в инженерных и научных расчётах. Основание натуральных логарифмов не является целым числом.
Единицы, производные от бита
Целые количества бит отвечают количеству состояний, равному степеням двойки.
Особое название имеет 4 бита — ниббл (полубайт, тетрада, четыре двоичных разряда), которые вмещают в себя количество информации, содержащейся в одной шестнадцатеричной цифре.
| Измерения в байтах | ||||||
|---|---|---|---|---|---|---|
| Десятичная приставка | Двоичная приставка | |||||
| Название | Символ | Степень | Название | Символ | Степень | |
| МЭК | ГОСТ | |||||
| байт | B | 10 0 | байт | B | байт | 2 0 |
| килобайт | kB | 10 3 | кибибайт | KiB | Кбайт | 2 10 |
| мегабайт | MB | 10 6 | мебибайт | MiB | Мбайт | 2 20 |
| гигабайт | GB | 10 9 | гибибайт | GiB | Гбайт | 2 30 |
| терабайт | TB | 10 12 | тебибайт | TiB | Тбайт | 2 40 |
| петабайт | PB | 10 15 | пебибайт | PiB | Пбайт | 2 50 |
| эксабайт | EB | 10 18 | эксбибайт | EiB | Эбайт | 2 60 |
| зеттабайт | ZB | 10 21 | зебибайт | ZiB | Збайт | 2 70 |
| йоттабайт | YB | 10 24 | йобибайт | YiB | Йбайт | 2 80 |
Следующей по порядку популярной единицей информации является 8 бит, или байт (о терминологических тонкостях написано ниже). Именно к байту (а не к биту) непосредственно приводятся все большие объёмы информации, исчисляемые в компьютерных технологиях.
Такие величины как машинное слово и т. п., составляющие несколько байт, в качестве единиц измерения почти никогда не используются.
Килобайт
Для измерения больших количеств байтов служат единицы «килобайт» = 1000 байт и «Кбайт» [3] (кибибайт, kibibyte) = 1024 байт (о путанице десятичных и двоичных единиц и терминов см. ниже). Такой порядок величин имеют, например:
Объём информации, получаемой при считывании дискеты «3,5″ высокой плотности» равен 1440 Кбайт (ровно); другие форматы также исчисляются целым числом Кбайт.
Мегабайт
Единицы «мегабайт» = 1000 килобайт = 1000000 байт и «Мбайт» [3] (мебибайт, mebibyte) = 1024 Кбайт = 1 048 576 байт применяются для измерения объёмов носителей информации.
Объём адресного пространства процессора Intel 8086 был равен 1 Мбайт.
Современные жёсткие диски имеют объёмы, выражаемые в этих единицах минимум шестизначными числами, поэтому для них применяются гигабайты.
Гигабайт
Единицы «гигабайт» = 1000 мегабайт = 1000000000 байт и «Гбайт» [3] (гибибайт, gibibyte) = 1024 Мбайт = 2 30 байт измеряют объём больших носителей информации, например жёстких дисков. Разница между двоичной и десятичной единицами уже превышает 7 %.
Размер 32-битного адресного пространства равен 4 Гбайт ≈ 4,295 гигабайт. Такой же порядок имеют размер DVD-ROM и современных носителей на флеш-памяти. Размеры жёстких дисков уже достигают сотен и тысяч гигабайт.
Для исчисления ещё больших объёмов информации имеются единицы терабайт—тебибайт ( 10 12 и 2 40 соответственно), петабайт—пебибайт ( 10 15 и 2 50 соответственно) и т. д.
Что такое «байт»?
В принципе, байт определяется для конкретного компьютера как минимальный шаг адресации памяти, который на старых машинах не обязательно был равен 8 битам (а память не обязательно состоит из битов — см., например: троичный компьютер). В современной традиции, байт часто считают равным восьми битам.
В таких обозначениях как Кбайт (русское) или KB (английское) под байт (B) подразумевается именно 8 бит, хотя сам термин «байт» не вполне корректен с точки зрения теории.
Во французском языке используются обозначения o, Ko, Mo и т. д. (от слова octet) дабы подчеркнуть, что речь идёт именно о 8 битах.
Чему равно «кило»?
Долгое время разнице между множителями 1000 и 1024 старались не придавать большого значения. Во избежание недоразумений следует чётко понимать различие между:
Последние по определению равны соответственно 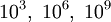
В качестве терминов для «Кбайт», «Мбайт», «Гбайт» и т. д. МЭК предлагает «кибибайт», «мебибайт», «гибибайт» и т. д., однако эти термины критикуются за непроизносимость и не встречаются в устной речи.
В различных областях информатики предпочтения в употреблении десятичных и двоичных единиц тоже различны. Причём, хотя со времени стандартизации терминологии и обозначений прошло уже несколько лет, далеко не везде стремятся прояснить точное значение используемых единиц. В английском языке для «киби»=1024 иногда используют прописную букву K, дабы подчеркнуть отличие от обозначаемой строчной буквой приставки СИ кило. Однако, такое обозначение не опираются на авторитетный стандарт, в отличие от российского ГОСТа касательно «Кбайт».
Примечания
См. также
Ссылки
Полезное
Смотреть что такое «Единицы измерения информации» в других словарях:
Единицы количества информации — Единицы измерения информации служат для измерения объёма информации величины, исчисляемой логарифмически.[1] Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество… … Википедия
Единицы измерения ёмкости носителей и объёма информации — Единицы измерения информации служат для измерения различных характеристик связанных с информацией. Чаще всего измерение информации касается измерения ёмкости компьютерной памяти (запоминающих устройств) и измерения объёма данных, передаваемых по… … Википедия
Единицы измерения количества информации — Единицы измерения информации служат для измерения объёма информации величины, исчисляемой логарифмически.[1] Это означает, что когда несколько объектов рассматриваются как один, количество возможных состояний перемножается, а количество… … Википедия
Единицы измерения — В физике и технике единицы измерения (единицы физических величин, единицы величин[1]) используются для стандартизованного представления результатов измерений. Использование термина единица измерения противоречит рекомендациям метрологических… … Википедия
Единицы измерения объёма выполненного перевода — Объём письменного перевода может оцениваться либо по времени, затраченному на перевод, либо по объёму текста. В первом случае единицей измерения служит час (астрономический). Применяется относительно редко, в основном, когда переводятся изменения … Википедия
ЕДИНИЦЫ ИЗМЕРЕНИЯ ОБЪЕМОВ ИНФОРМАЦИИ — В основе измерения больших объемов информации лежит байт. Более крупные единицы измерения: килобайт (1 Кбайт = 1024 байта), мегабайт (1 Мбайт = 1024 Кбайт = 1048576 байт), гигабайт (1 Гбайт = 1024 Мбайт = 1073741824 байт). Например, на листе… … Словарь бизнес-терминов
ЕДИНИЦЫ ИЗМЕРЕНИЯ И ЕДИНИЦЫ АНАЛИЗА В КОНТЕНТ-АНАЛИЗЕ — элементы логич. модели предмета контент анлиза (см.). Содержание текста может быть измерено при помощи двух типов измерения (мер): единиц протяженности и единицы частоты. Единицы протяженности характеризуют содержание в целом, без учета его… … Российская социологическая энциклопедия
Нат (единица измерения информации) — Нат больше бита, но немного меньше трита. Жёлтая кривая график логарифма. Нат одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Применяется в … Википедия
Нат (Единица измерения информации) — Нат больше бита, но немного меньше трита. Жёлтая кривая график логарифма. Нат одна из единиц измерения информации. Определяется через натуральный логарифм, в отличие от других единиц, где основание логарифма является целым числом. Применяется в … Википедия
Информатика. 7 класс
Конспект урока
Единицы измерения информации
Перечень вопросов, рассматриваемых в теме:
Каждый символ информационного сообщения несёт фиксированное количество информации.
Единицей измерения количества информации является бит – это наименьшаяединица.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Формулы, которые используются при решении типовых задач:
Информационный объём сообщения определяется по формуле:
I – объём информации в сообщении;
К – количество символов в сообщении;
i – информационный вес одного символа.
Теоретический материал для самостоятельного изучения.
Любое сообщение несёт некоторое количество информации. Как же его измерить?
Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.
Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.
Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.
Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.
Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.
Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.
Составим краткую запись условия задачи и решим её:
Информационный вес одного символа этого алфавита составляет 4 бита.
Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.
Математически это произведение записывается так: I = К · i.
Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?
I = 180 · 5 = 900 бит.
Итак, информационный вес всего сообщения равен 900 бит.
В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.
I = 23 · 8 = 184 бита.
Значит, сообщение весит 184 бита.
Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.
Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.
1 Кб (килобайт) = 1024 байта= 2 10 байтов
1 Мб (мегабайт) = 1024 Кб = 2 10 Кб
1 Гб (гигабайт) = 1024 Мб = 2 10 Мб
1 Тб (терабайт) =1024 Гб = 2 10 Гб
Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.
Материал для углубленного изучения темы.
Как текстовая информация выглядит в памяти компьютера.
Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?
Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.
Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.
В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.
Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:
01100110 01101001 01101100 01100101.
А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:
01100100 01101001 01110011 01101011?
В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.
Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.
Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.
Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.
Разбор решения заданий тренировочного модуля
№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?
№2. Выразите в килобайтах 2 16 байтов.
2 6 = 64, а 2 10 байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.
№3. Тип задания: выделение цветом
8 х = 32 Кб, найдите х.
Лекция-2 «Информация: понятие, представление, единицы измерения информации» (1 курс специальности СД)
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Специальность 34.02.01 «Сестринское дело»
« Информация: понятие, представление, единицы измерения информации »
Представление и кодирование информации
Кодирование информации — это процесс преобразования информации из одной формы представления в другую.
Аналоговая форма представляет непрерывный сигнал, который меняется пропорционально изменению информации, т. е. информация кодируется изменяющимся во времени напряжением или током. Такое представление информации используется в аналоговых вычислительных машинах (АВМ). Однако эти машины не получили дальней шего развития в основном из-за невысокой точности вычислений.
Цифровая форма представления информации используется в цифровых вычислительных машинах (ЦВМ). В этих машинах информация кодируется цифрами. В виде цифр представляются различные виды информации: числа, буквы, звук, изображения.
В ЦВМ применяется двоичная система счисления. В этой системе используются только две цифры: 0 и 1.
Имеются и другие системы счисления: восьмеричная, десятичная, шестнадцатеричная и др. Но двоичная система отлича- ется от них высокой надежностью представления информации. Распознать два состояния (0 или 1) значительно проще, чем, например, 10 состояний. В живых системах также для передачи информации используется двоичное кодирование информации в виде потенциала покоя и потенциала действия, биологические 0 и 1.
В двоичной системе счисления можно выполнять все математические действия, как и в привычной нам десятичной системе счисления. В ЦВМ для кодирования двоичных знаков используются два уровня напряжения.
Обычно, единица — это высокий уровень напряжения, порядка 5 В, а низкий уровень (меньше 0,8 В) — ноль. Имеются специальные устройства для преобразования аналоговой формы в цифровую, и наоборот.
Такие устройства называются соответственно аналого-цифровым преобразователем (АЦП) и цифро-аналоговым преобразователем (ЦАП).
Процесс преобразования непрерывных сигналов в цифровую форму состоит из трех этапов: дискретизации, квантования и кодирования.
Дискретизация — это процесс разбиения сигнала на отдельные составляющие, взятые через равные промежутки времени, величины которых зависят от частоты дискретизации (рис. 1.2, а).
Информация — это сведения об объектах и явлениях окружающего мира, уменьшающие степень неопределённости знаний об этих объектах или явлениях.
В роли источника или приемника может быть любой объект материального мира: человек, устройство, животное, растение. То есть информация всегда предназначена конкретному объекту.
Источник информации — это объект, порождающий информацию и представляющий её в виде сообщения.
Приемник информации — это объект, принимающий сообщение и способный правильно его интерпретировать.
Под словом «кодирование» понимают процесс представления информации, удобный для её хранения и/или передачи. Следовательно, запись текста на естественном языке можно рассматривать как способ кодирования речи с помощью графических элементов (букв, иероглифов). Записанный текст является кодом, заключающим в себе содержание речи, т. е. информацию.
Код — система условных знаков (символов ), предназначенных для представления информации в соответствии с определенными правилами.
Кодирование — переход от одной формы представления информации к другой, наиболее удобной для её хранения, передачи или обработки.
Декодирование — процесс по восстановлению первоначальной формы представления информации, т. е. операция, обратная кодированию.
При кодировании ставятся разные цели и, соответственно, применяются различные способы кодирования.
Наиболее распространенные цели кодирования:
1) экономность (сократить запись);
2) надежность (засекретить информацию);
Чаще всего кодированию подвергаются тексты на естественных языках (русском, английском и пр.).
Существуют три основных способа кодирования текста:
1) графический — с помощью специальных рисунков или значков;
2) числовой — с помощью чисел;
3) символьный — с помощью символов того же алфавита, что и исходный текст.
Процесс чтения текста — это обратный по отношению к письму процесс, при котором письменный текст преобразуется в устную речь. Чтение можно назвать декодированием письменного текста.
А теперь обратим внимание на то, что может существовать много способов кодирования одного и того же текста на одном и том же языке.
Русский текст мы привыкли записывать с помощью русского алфавита. Но то же самое можно сделать, используя латинский алфавит. Иногда так приходится поступать, отправляя SMS по мобильному телефону, на котором нет русских букв, или электронное письмо на русском языке за границу, если у адресата нет русифицированного программного обеспечения. Например, фразу «Здравствуй, дорогой Саша!» приходится писать так: « Zdravstvui , dorogoi Sasha !».
Существует множество способов кодирования. Например, стенография — быстрый способ записи устной речи. Ею владеют лишь немногие специально обученные люди — стенографисты. Они успевают записывать текст синхронно с речью выступающего человека. В стенограмме один значок обозначает целое слово или сочетание букв. Скорость стенографического письма превосходит скорость обычного в 4-7 раз. Расшифровать (декодировать) стенограмму может только сам стенографист.
Для кодирования одной и той же информации могут быть использованы разные способы; их выбор зависит от ряда обстоятельств: цели кодирования, условий, имеющихся средств.
Заметим, что две эти записи, эквивалентные по смыслу, используют разные языки: первая — естественный русский язык, вторая — формальный язык математики, не имеющий национальной принадлежности. Переход от представления на естественном языке к представлению на формальном языке можно также рассматривать как кодирование. Человеку удобно использовать для кодирования чисел десятичную систему счисления, а компьютеру — двоичную систему.
Шифрование представляет собой процесс превращения открытого текста в зашифрованный, а дешифрование — процесс обратного преобразования, при котором восстанавливается исходный текст. Шифрование — это тоже кодирование, но с засекреченным методом, известным только источнику и адресату. Методами шифрования занимается наука криптография .
Шифрование — медот защиты любой информации от несанкционированного доступа, просмотра, а также её использования, основанный на преобразовании данных в зашифрованный формат.
Криптография — это наука о методах и принципах передачи и приема зашифрованной с помощью специальных ключей информации.
Ключ — секретная информация, используемая криптографическим алгоритмом при шифровании/расшифровке сообщений.
Единицы измерения информации.
Для информации существуют свои единицы измерения информации. Если рассматривать сообщения информации как последовательность знаков, то их можно представлять битами, а измерять в байтах, килобайтах, мегабайтах, гигабайтах, терабайтах и петабайтах.
Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.
Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.
1бит – это количество информации, содержащейся в сообщении, которое вдвое уменьшает неопределенность знаний о чем-либо.
Байт – основная единица измерения количества информации.
Байтом называется последовательность из 8 битов.
Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.
Производные единицы измерения количества информации
1 килобайт (Кб)=1024 байта =2 10 байтов
1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов
1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов
1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов
Методы измерения количества информации
Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:
Алфавитный подход к измерению количества информации
При этом подходе отвлекаются от содержания (смысла) информации и рассматривают ее как последовательность знаков определенной знаковой системы. Набор символов языка, т.е. его алфавит можно рассматривать как различные возможные события. Тогда, если считать, что появление символов в сообщении равновероятно, по формуле Хартли можно рассчитать, какое количество информации несет в себе каждый символ:
Вероятностный подход к измерению количества информации
Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

I – количество информации,
N – количество возможных событий,
P i – вероятность i-го события.
Если подбросить монету и проследить, какой стороной она упадет, то мы получим определенную информацию. Обе стороны монеты “равноправны”, поэтому одинаково вероятно, что выпадет как одна, так и другая сторона. В таких случаях говорят, что событие несет информацию в 1 бит.
Если положить в мешок два шарика разного цвета, то, вытащив вслепую один шар, мы также получим информацию о цвете шара в 1 бит.
Задача 1.
Шар находится в одной из четырех коробок. Сколько бит информации несет сообщение о том, в какой именно коробке находится шар.
Имеется 4 равновероятных события ( N=4 ).
Задача 2.
Чему равен информационный объем одного символа русского языка?
В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа.I=log 2 N =log 2 32=5 битов ( 2 5 =32 ).
Задача 3.
Чему равен информационный объем одного символа английского языка?
Задача 4.
Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?
С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.
Задача 5.
Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.
Задача 6.
Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.
Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:
Задача 7.
Задача 8.
Оцените информационный объем следующего предложения:
Тяжело в ученье – легко в бою!
Представление информации в различных системах счисления
В непозиционной системе счисления цифры не изменяют своего значения при изменении их расположения в числе. Примером непозиционной системы может служить римская система, в которой независимо от местоположения одинаковый символ имеет неизменное значение (например, символ X в числе XXV ).
Количество ( р ) различных символов, используемых для изображения числа в позиционной системе счисления, называется основанием системы счисления.
Основание показывает, во сколько раз изменяется количественное значение цифры при перемещении ее в младший или старший разряд.
Набор символов, используемый для обозначения цифр, называется алфавитом.
Любое число N в позиционной системе счисления можно представить в следующем виде:
N p =±( a k −1 ⋅ p k −1 + a k −2 ⋅ p k −2 +. + a 0 ⋅ p 0 + a −1 ⋅ p −1 +. + a − m ⋅ p − m )
Нижние индексы определяют местоположение цифры в числе (разряд):
Свернутой формой записи числа называется запись в виде:
Свернутой формой записи чисел мы и пользуемся в повседневной жизни, ее называют естественной илицифровой.
Десятичная система счисления
Десятичная система счисления наиболее распространенная система счисления в мире. Используется при повседневном счете. Для записи чисел используются арабские цифры (0, 1, 2, 3, 4, 5, 6, 7, 8, 9).
Число в десятичной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 10 ), в качестве коэффициентов которых выступают цифры данного числа.
765,345 10 =7 ⋅ 10 2 +6 ⋅ 10 1 +5 ⋅ 10 0 +3 ⋅ 10 −1 +4 ⋅ 10 −2 +5 ⋅ 10 −3
Двоичная система счисления
Двоичную систему счисления широко применяют в вычислительной технике. К ее достоинствам относятся:
— возможность использования аппарата булевой алгебры для выполнения логических преобразований информации;
— возможность использования простейших правил арифметики.
Число в двоичной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 2 ), в качестве коэффициентов которых выступают цифры данного числа.
1011,01 2 =1 ⋅ 2 3 +0 ⋅ 2 2 +1 ⋅ 2 1 +1 ⋅ 2 0 +0 ⋅ 2 −1 +1 ⋅ 2 −2
Восьмеричная система счисления
Восьмеричная система чаще всего используется в областях, связанных с цифровыми устройствами. Характеризуется лёгким переводом восьмеричных чисел в двоичные и обратно, путём замены восьмеричных чисел на триады (группы по 3 разряда) двоичных. Ранее широко использовалась в программировании и вообще компьютерной документации, однако в настоящее время почти полностью вытеснена шестнадцатеричной.
Число в восьмеричной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 8 ), в качестве коэффициентов которых выступают цифры данного числа.
567,12 8 =5 ⋅ 8 2 +6 ⋅ 8 1 +7 ⋅ 8 0 +1 ⋅ 8 −1 +2 ⋅ 8 −2
Шестнадцатеричная система счисления
Шестнадцатеричная система счисления, на сегодняшний день является наиболее популярным средством компактной записи двоичных чисел. Очень широко используется при разработке и проектировании цифровой техники.
Число в шестнадцатеричной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 16 ), в качестве коэффициентов которых выступают цифры данного числа.
10 FC 16 =1 ⋅ 16 3 +0 ⋅ 16 2 + F ⋅ 16 1 + C ⋅ 16 0
Помимо рассмотренных выше позиционных систем счисления, существуют и другие, например:
— троичная ( 0,1,2 );
В системах счисления с основанием больше 10 для представления чисел после цифр 0,1,2,…,9 используют латинские буквы в алфавитном порядке: А ( 10 ), В ( 11 ), С ( 12 ) и т. д.
1) Представим двоичное число 10110,101 2 в виде суммы слагаемых, а затем произведем их сложение:
10110,101 2 =1 ⋅ 2 4 +0 ⋅ 2 3 +1 ⋅ 2 2 +1 ⋅ 2 1 +0 ⋅ 2 0 +1 ⋅ 2 −1 +0 ⋅ 2 −2 +1 ⋅ 2 −3 ==16+0+4+2+0+0,5+0+0,125=22,625 10
Таким образом, 10110,101 2 =22,625 10
3) Вычислим сумму чисел 2 F 16 , 232 4 и 53 8 , представив результат в десятичной системе счисления.
Переведем все числа в десятичную систему счисления, и сложим их:
2 F 16 =2 ⋅ 16 1 +15 ⋅ 16 0 =32+15=47 10
232 4 =2 ⋅ 4 2 +3 ⋅ 4 1 +2 ⋅ 4 0 =32+12+2=46 10
53 8 =5 ⋅ 8 1 +3 ⋅ 8 0 =40+3=43 10
47 10 +46 10 +43 10 =136 10
Таким образом, 2 F 16 +232 4 +53 8 =136 10
Перевод числа из десятичной системы счисления в другую позиционную систему
Правило перевода целой части числа состоит из следующих этапов:
— число N делится на новое основание р ;
— полученный остаток запоминается или записывается (это будет цифра младшего разряда);
— целая часть полученного частного снова делится на р ;
— опять запоминаем полученный остаток (это будет цифра следующего разряда) и т. д.
Правило перевода дробной части числа состоит из следующих этапов:
— дробная часть числа умножается на основание р ;
— запоминается или записывается цифра результата, переносимая в целую часть;
— оставшаяся дробная часть числа умножается на основание р ;
— снова фиксируется цифра результата, переносимая в целую часть, и т. д.
Такое последовательное умножение продолжается до тех пор, пока в дробной части не будет получен ноль или достигнута требуемая точность, например 5 знаков после запятой. Результат формируется в виде последовательной записи зафиксированных цифр переносов в целую часть в том порядке, в котором они были получены.
1) Переведем число 75 из десятичной системы в двоичную, восьмеричную и шестнадцатеричную:
Замечание : остаток 11 10 записывается шестнадцатеричной цифрой B 16 .
Ответ: 75 10 =1001011 2 =113 8 =4 B 16
Замечание : число 13 10 записывается шестнадцатеричной цифрой D 16 .
Ответ: 0,8125 10 =0,1101 2 =0,64 8 =0, D 16
Для чисел, имеющих как целую, так и дробную части, перевод из десятичной системы счисления в другую осуществляется отдельно для целой и дробной частей по правилам, указанным выше. Необходимо отдельно преобразовать целую и дробную части числа и соединить их через запятую.
Ответ: 194,125 10 =110000010,001 2
Для перевода восьмеричного числа в двоичное достаточно каждую цифру этого числа заменить двоичной триадой (три разряда) в соответствии с таблицей (если нужно, слева дописывается дополнительный ноль).
734,46 8 =111011100,100110 2
Для перевода двоичного числа в восьмеричное следует воспользоваться следующим алгоритмом:
— разделить целую часть числа на триады от младших разрядов к старшим (влево от запятой);
— разделить дробную часть на триады в обратном направлении (вправо от запятой);
— заменить каждую триаду двоичных чисел соответствующей восьмеричной цифрой по таблице, предложенной выше;
— недостающие до триады позиции заполнить незначащими нуями.
1010,11111 2 =001010,111110 2 =12,76 8
Подобным свойством обладают и шестнадцатеричные цифры. Все шестнадцатеричные цифры (от 0 до F ) можно записать при помощи четырех двоичных разрядов ( тетрады ) (см. таблицу выше).
10101001,10111 2 =10101001,10111000 2 = A 9, B 8 16
Если в качестве промежуточной системы использовать двоичную, то существенно упрощается перевод из восьмеричной системы в шестнадцатеричную и обратно. Это показано в следующем примере.
A 2 =010111101,000011100
A 2 =10111101,00001110
Форматы представления чисел в компьютере
Для хранения чисел в памяти компьютера используется два формата: целочисленный (естественная форма) и с плавающей точкой (нормализованная форма) (точка — разделительный знак для целой и дробной части числа).
В форме с фиксированной запятой числа изображаются в виде последовательности цифр с постоянным для всех чисел положением запятой (или точки), отделяющей целую часть от дробной.
Эта форма проста и привычна для большинства пользователей, но имеет небольшой диапазон представления чисел и поэтому не всегда пригодна при вычислениях. Если же в результате какой-либо арифметической операции получается число, выходящее за допустимый диапазон, то происходит переполнение разрядной сетки, и все дальнейшие вычисления теряют смысл.
Если число вышло за указанные границы, произойдет переполнение! Поэтому при работе с большими целыми числами под них выделяется больше места, например 4 байта.
Нормализованная форма представления чисел обеспечивает огромный диапазон их записи и является основной в современных ЭВМ.
Представление целого положительного числа в компьютере
Для представления целого положительного числа в компьютере используется следующее правило:
Представление целого отрицательного числа в компьютере
Для представления целого отрицательного числа в компьютере используется следующее правило:
Обратный код для положительного двоичного числа совпадает с его прямым кодом, а для отрицательного числа нужно во всех разрядах, кроме знакового, нули заменить единицами и наоборот.
Дополнительный код для положительного числа совпадает с его прямым кодом, а для отрицательного числа образуется путем прибавления 1 к обратному коду.
Отрицательное число может быть представлено в виде 2 или 4 байт.
— 135 10 10000111 (перевод десятичного числа без знака в двоичный код);
— 0000000010000111 (дополнение двоичного числа нулями слева в пределах формата);
— 0000000010000111 1111111101111000 (перевод в обратный код);
— 1111111101111000 1111111101111001 (перевод в дополнительный код).
Представление вещественного (действительного) числа в компьютере
Вещественное число может быть представлено в экспоненциальном виде, например:
16000000 10 =0,16 ⋅ 10 8
− 0,0000156 10 =−0,156 ⋅ 10 −4
В этом формате вещественное число ( R ) представляется в виде произведения мантиссы ( m ) и основания системы счисления ( P ) в целой степени ( n ), называемой порядком.
Мантисса должна быть правильной дробью, у которой первая цифра после точки (запятой в обычной записи) отлична от нуля. Если это требование выполнено, то число называется нормализованным.
При представлении в компьютере действительного числа с плавающей точкой тоже используется нормализованная мантисса и целый порядок. И мантисса и порядок представляются в двоичном виде, как это было описано выше.
Для размещения вещественного числа обычно используется 2 или 4 байта.
Чем больше разрядов отводится под запись мантиссы, тем выше точность представления числа.








