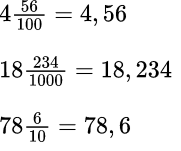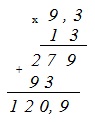Как называется числа с запятыми
Десятичная запятая
Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.
| обыкновенная дробь | десятичная дробь |
|---|---|
| 4 /10 | 0,4 |
| 79 395 /1000 | 79,395 |
Очевидно, в начало целой части и/или в конец дробной части можно дописывать сколько угодно нулей.
Существуют также бесконечные десятичные дроби — периодические и непериодические. Например, ⅓ записывается как бесконечная периодическая дробь 0,3333… или 0,(3). А число π записывается как бесконечная непериодическая дробь 3,141592…
Периодическая десятичная дробь называется чистой периодической дробью, если её период (группа повторяющихся цифр) начинается сразу после запятой, а период может содержать любое конечное число цифр. Так, дробь 1,(3) — чистая периодическая дробь. Если периодическая десятичная дробь содержит ещё число, заключённое между целой частью и периодом, то такая периодическая дробь называется смешанной; число периодической дроби, стоящее между целой частью и периодом, называется предпериодом этой дроби.
Очевидно, что всякая периодическая дробь является рациональным числом вида 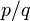
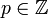
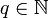
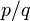
Произношение десятичных дробей
В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» («целая»), потом десятичная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.).
Однако на практике часто встречается такое произношение: целая часть, союз «и», дробная часть.
Десятичные дроби
Обыкновенную дробь (или смешанное число), у которой знаменатель является единицей с одним или более нулями (т. е. 10, 100, 1000 и т. д.):
можно записать в более простой форме: без знаменателя, разделяя целую и дробную части друг от друга запятой (при этом считают, что целая часть правильной дроби равна 0). Сначала записывается целая часть, затем ставится запятая, и после неё записывается дробная часть:
Записанные в такой форме обыкновенные дроби (или смешанные числа) называются десятичными дробями.
Чтение и запись десятичных дробей
Десятичные дроби записывают по тем же правилам, по которым записывают натуральные числа в десятичной системе счисления. Это означает, что в десятичных дробях, как и в натуральных числах, каждая цифра выражает единицы, которые в десять раз больше соседних единиц, стоящих справа.
Рассмотрим следующую запись:
Цифра 8 означает простые единицы. Цифра 3 означает единицы, в 10 раз меньшие, чем простые единицы, т. е. десятые доли. 4 означает сотые доли, 2 — тысячные и т. д.
Цифры, которые стоят справа после запятой, называются десятичными знаками.
3,1 читается так: три целых одна десятая ;
Чтобы лучше понять правила записи и чтения десятичных дробей, рассмотрим таблицу разрядов и приведённые в ней примеры записи чисел:
Обратите внимание, после запятой в записи десятичной дроби получается столько цифр, сколько нулей содержит знаменатель соответствующей ей обыкновенной дроби:
Десятичные дроби
теория по математике 📈 числа и вычисления
Десятичная дробь — дробь, которая представляет собой способ представление числа в виде записи числа с запятой, где цифры перед запятой называются целой частью, а цифры после запятой – дробной частью (десятичной частью).
Десятичные дроби получают из записи обыкновенных дробей со знаменателем 10, 100, 1000 и так далее. Например, десятичные дроби:
4,56 – четыре целых пятьдесят шесть сотых 18,234 – восемнадцать целых двести тридцать четыре тысячных 78,6 – семьдесят восемь целых шесть десятых
Чтение десятичных дробей
Чтение десятичной части (десятых, сотых и так далее) зависит от количества цифр после запятой. Если цифра одна, то читают – десятых (в числе десять — один нуль, это соответствует одной цифре). Если две цифры после запятой, то читают – сотых (в сотне два нуля).
Десятичные дроби получаются из обыкновенных дробей:
Сложение (вычитание) десятичных дробей
Чтобы сложить (вычесть) в столбик две десятичные дроби нужно:
Если складывают (вычитают) целое число и десятичную дробь, то нужно поставить запятую после целого числа и приписать необходимое количество нулей после запятой.
Пример №1. Запись, где запятая под запятой и соответствующий разряд под соответствующим.
34,145 + 5,678 = 39,823
Пример №2. Запись, где также запятая под запятой, а во втором числе дописан нуль, чтобы уравнять количество знаков после запятой.
Пример №3. В первом слагаемом нет десятичной части, поэтому, после числа 56 поставили запятую и добавили нужное количество нулей.
Умножение десятичных дробей
При умножении двух десятичных дробей в столбик необходимо:
Пример №4. Запись выполнена так, что цифры по правому краю записаны ровно одна под одной, то есть как при обычном умножении чисел в столбик. Умножение выполнено без учета запятой. В ответе справа отделены 4 цифры запятой, так как в первом множителе их 3 после запятой, а во втором – одна, в двух множителях вместе – четыре.
0,125 × 2,3 00375 0250 0,2875
Пример №5. Здесь показано умножение десятичной дроби и целого числа. Умножение выполнено без учета запятой. В ответе отделена справа запятой только одна цифра, так как только в первом множителе есть десятичная часть с одной цифрой после запятой.
Умножение десятичных дробей на 10, 100, 1000…
Чтобы умножить десятичную дробь на 10, 100, 1000 и так далее, нужно перенести запятую вправо на столько цифр, сколько нулей у множителя. Умножение в данном случае выполняется в строчку.
Пример №6. 2,456 × 10 = 24,56 Запятую в десятичной дроби перенесли вправо на 1 цифру, так как у 10 один нуль.
Пример №7. 0,45678 × 100 = 45,678 Запятую перенесли вправо на 2 цифры, так как у 100 два нуля. Нуль, стоящий в начале десятичной дроби, убрали, так как впереди целой части, отличной от нуля он не пишется.
Пример №8. 9,46 × 1000 = 9460 в данном случае при переносе запятой на три цифра не хватило одной, поэтому в конце числа приписали нуль, и в ответе получилось целое число.
Умножение десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При умножении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 (и так далее) нужно перенести запятую на столько цифр влево, сколько цифр в данной разрядной единице после запятой. Умножение обычно выполняется в строчку устно.
Пример №9. 983,7821 × 0,01= 9,837821 Переносим запятые влево на 2 цифры, так как в числе 0,01 две цифры после запятой.
Пример №10. 8,7654 × 0,1 = 0,87654 Перенесли на 1 цифру влево, так как в числе 0,1 одна цифра после запятой. В данном случае перед 8 появился нуль, так как при переносе запятой слева цифр не оказалось.
Пример №11. 7,98 × 0,0001 = 0,000798 При переносе влево на 4 цифры не хватило трех, поэтому впереди поставили нули, а также нуль образуется и в целой части.
Деление десятичных дробей
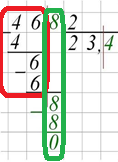
Пример №12. Деление десятичной дроби на целое число. 46,8 : 2 = 23,4
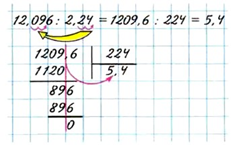
Пример №13. Деление десятичной дроби на десятичную дробь. 12,096 : 2,24 = 5,4 Из данного примера видно, что деление десятичных дробей обязательно сводится к делению на целое число.
Пример №14. 276,3 : 0,003 = 276300 : 3 = 92100. Здесь видно, что не хватает двух цифр в числе 276,3 и поэтому при переносе запятой к нему приписали два нуля. Затем выполнили деление двух целых чисел.
Деление десятичной дроби на 10, 100, 1000…
При делении десятичной дроби на 10,100, 1000 и так далее нужно перенести запятую на столько цифр влево, сколько нулей в данном числе. Деление выполняется в строчку устно.
Пример №16. 134,987 : 1000 = 0,134987 Перенесли запятую на три цифры влево, так как у 1000 три нуля. В целой части поставили нуль, так как цифр не хватило.
Пример №17. 7,234 : 100 = 0,07234 Перенесли запятую влево на две цифры. Так как цифр не хватало, то недостающие заменили нулями.
Деление десятичной дроби на разрядную единицу 0,1; 0,01; 0,001…
При делении десятичной дроби на разрядную единицу 0,1; 0,01; 0,001 и так далее нужно перенести запятую на столько цифр вправо, сколько цифр в данной разрядной единице после запятой. Деление обычно выполняется в строчку устно.
Пример №19. 41,234 : 0,01 = 4123,4 Перенос запятой на 2 цифры вправо, так как в числе 0,01 две цифры после запятой.
Пример №20. 56,91 : 0,001 = 56910 При переносе запятой на три цифры вправо приписали один нуль, так как одной цифры не хватило.
Сформируем из чисел ряд от наименьшего из них до наибольшего. Для этого сначала разделим их на положительные и отрицательные. И сразу получим наибольшее в ряду (поскольку оно единственное больше нуля): 0,021.
Три оставшихся отрицательных распределим по их модулям. Известно, что из двух отрицательных чисел больше то, у которого модуль меньше. Тогда получаем, что –0,304
pазбирался: Даниил Романович | обсудить разбор | оценить
Для получения результата необходимо последовательно выполнить математические действия в соответствии с их приоритетом.
Выполняем возведение в степень. Получаем числа, состоящие из единицы и следующего за ней количества нулей, равного показателю степени. При этом знаки «–» в скобках исчезают, поскольку показатели степеней четные. Получаем:
Выполняем умножение. Для этого в числе 0,3 переносим десятичную запятую на 4 знака вправо (так как в 10000 четыре нуля), а к 4 дописываем, соответственно, 2 нуля. Получаем:
Выполняем сложение –3000+400. Поскольку это числа с разными знаками, то вычитаем из большего модуля меньший и перед результатом ставим «–», поскольку число с большим модулем отрицательное. Получаем:
Так как оба числа отрицательные, то складываем их модули и перед результатом ставим «–». Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Это задание требует простого умения выполнять арифметические действия с десятичными дробями.
Сначала выполняем умножение. Умножаем –13 и –9,3 в столбик без учета знаков «–» перед сомножителями. В полученном произведении отделяем одну – последнюю – цифру десятичной запятой:
Знак произведения будет положительным, поскольку умножаются два отрицательных числа. Получаем:
Эту разность можно вычислить в столбик, но можно и устно. Выполним это действие в уме: вычитаем отдельно целые части и десятичные. Получаем:
pазбирался: Даниил Романович | обсудить разбор | оценить
Задачу можно решать разными путями, а именно менять последовательность действий, но этот вариант решения рекомендуется для тех, кто уверен в своих возможностях и знает математику на отлично. Для остальных мы рекомендуем выполнить последовательно действия в числителе и знаменателе, а затем разделить числитель на знаменатель. Числитель вычислять в данном примере нет необходимости, это число 9.
Вычислим значение знаменателя:
Можно произвести вычисления в столбик, тогда получим:
Либо перевести дробь к простому виду:
4,5 • 2,5 = 4½ • 2 ½ = 9 / 2 • 5 / 2 = 45 / 4
Последний случай предпочтительней, так как для дальнейшей операции — деления числителя на знаменатель задача упрощается. Делим числитель на знаменатель, умножая числитель на перевернутую дробь в знаменателе:
9 / ( 45 / 4 ) = ( 9 / 1 ) • ( 4 / 45 ) = ( 9 • 4 ) / (1 • 45 )
9 и 45 можно сократить на 9:
( 9 • 4 ) / (1 • 45 ) = ( 1 • 4 )/ (1 • 5 ) = 4 / 5 = 8 / 10 = 0,8
pазбирался: Даниил Романович | обсудить разбор | оценить
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Десятичные дроби — для чайников
Действия с десятичными дробями – деление умножение, сложение, вычитание, сравнение. Разбор примеров.
Между прочим, большинство ошибок на экзаменах происходят как раз из-за незнания простейших действий вроде этих.
Так что читай эту статью и отрабатывай скиллы.
Десятичные дроби — коротко о главном
1. Определение
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени.
2. Конечная и бесконечная десятичная дробь
Десятичная дробь может быть:
3. Свойства десятичных дробей
4. Сложение десятичных дробей
Сложение происходит, как и сложение натуральных чисел в столбик, при этом запятая в ответе ставиться четко на том же месте, как и в складываемых числах.
5. Вычитание десятичных дробей
Так же, как и при сложении, при вычитании десятичные дроби записываются «столбиком»:
6. Умножение десятичных дробей
Десятичные дроби также записываются в столбик и умножаются как обыкновенные числа. При умножении нам неважно, стоят ли запятые под запятыми и так далее.
Однако, удобно, когда числа выровнены по правому краю – умножение происходит более упорядочено.
7. Деление десятичных дробей
Деление десятичной дроби на натуральное число
Деление десятичных дробей друг на друга
Десятичные дроби — подробнее
Конечно, ты знаешь, что такое обыкновенная дробь. Например, \( \displaystyle \frac<1><3>,\ \frac<1><4>,\frac<5><112>\).
Наравне с приведенными выше дробями существуют дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) и т.д.
Такие дроби можно записать намного удобнее и более кратко, то есть:
Данного вида дроби называются десятичными. Иными словами:
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Ты наверняка знаешь, что каждая цифра после запятой имеет свое название. На всякий случай напомню тебе про них, чтобы в дальнейшем мы говорили на одном языке:
Это огромное число читается по следующему алгоритму:
А теперь прочитаем все вместе – «\( 46\) целых одна тысяча двести тридцать четыре десятитысячные». Разобрался? Переходим к визуализации полученных знаний!
Итак, небольшая тренировка на понимание, что такое эта десятичная дробь! Нарисуй квадрат \( 10\) на \( 10\) и закрась какую-нибудь его часть равную:
Справился? Проверяем, что у тебя получилось.
Во-первых, квадрат \( 10\) на \( 10\) состоит из \( 100\) клеточек. Соответственно, \( 0.05\) – \( 5\) клеточек из \( 100\); \( 0,4\) – \( 40\) клеточек из \( 100\) и так далее.
С понятиями разобрались, теперь научимся переводить из десятичной дроби в обыкновенную и обратно.
Перевод из десятичной дроби в обыкновенную и обратно
Уверена, что ты с легкостью справился! А как насчет обратного перевода? Из обыкновенных в десятичные?
Попробуй свои силы на вот этих дробях:
Если ты со всем справился, можешь пропускать следующий абзац, а если где-то допустил ошибку, внимательно прочти о том, как легко и 100% правильно переводить дроби из обыкновенных в десятичные.
Разобрался? Посмотри еще раз эту маленькую «инструкцию»:
Я думаю, ты во всем-всем разобрался! Потренируемся? Попробуй поработать еще с вот этими дробями:
Виды десятичных дробей
Десятичная дробь может быть:
Поговорим сначала о конечных дробях.
Конечная десятичная дробь
Само собой понятно, что дроби \( \displaystyle \frac<8><10>,\ \frac<13><100>,\frac<49><1000>\) являются конечными, ведь знаменатель дроби уже представлен как единица с последующими нулями, и поэтому мы сразу можем сказать, что данную обыкновенную дробь можно перевести в конечную десятичную. А что ты скажешь насчет этой дроби: \( \displaystyle \frac<1><4>\)? Ее знаменатель далеко не единица с последующими нулями, но ты четко знаешь, что у нее есть десятичный «аналог»:
То есть, чтобы определить, можно ли перевести дробь в десятичную, необходимо умножить числитель и знаменатель на одно и то же число, такое, чтобы знаменатель стал равен \( 10\), \( 100\), \( 1000\) и так далее.
Усвоил? Постарайся представить в виде конечной десятичной дроби следующие обыкновенные дроби:
Сравним наши ответы:
Справился? Молодец. Выходим на новый уровень и переходим к бесконечным десятичным дробям.
Бесконечная десятичная дробь
Итак, бери калькулятор и дели \( 1\) на \( 17\). Поделил? Ты получил \( 0,05882352941\) и дальше окошко калькулятора не показывает… Это тоже является десятичной дробью, только данная десятичная дробь является бесконечной. Ты сейчас скажешь, а как же наше определение?
Десятичной дробью называется обыкновенная дробь, знаменателем которой является \( 10\) в какой-либо степени (первый пример – \( 10\) в первой степени, второй – \( 10\) во второй степени и т.д.).
Все очень просто и никаких противоречий с определением нет. В данном случае нам необходимо привести наш знаменатель к \( <<10>^
Бесконечной десятичной дробью называется обыкновенная дробь, в записи которой после запятой содержится бесконечное количество цифр.
Как правило, в задачах, где встречаются бесконечные десятичные дроби, просят указать ответ либо с округлением (например, до десятых, или до сотых), либо записать в виде обыкновенной дроби, то есть как \( \displaystyle \frac<1><17>\).
Подумай, какой самый популярный пример можно привести на тему «бесконечная десятичная дробь»? Правильно! Число \( \pi \) является бесконечной десятичной дробью. Во всем мире люди договорились, что для решения математических задач принято, что \( \pi =3,14\), но это далеко не так. Число \( \pi \) не имеет определенного завершения. Оно настолько бесконечно, что ежегодно в мире проводятся соревнования по запоминанию числа \( \pi \). Мировой рекорд по запоминанию знаков числа \( \pi \) после запятой принадлежит китайцу Лю Чао, который в 2006 году в течение 24 часов и 4 минут воспроизвёл 67 890 знаков после запятой без ошибки! Все 67 890 знаков после запятой мы приводить не будем, а приведем несколько сокращенную запись:
Думаю, этого хватит, чтобы оценить «масштабы» данного числа.
Наравне с бесконечными десятичными дробями существуют периодические десятичные дроби. Они так же не имеют конца, но последующие числа в них повторяются, например, попробуй перевести в десятичную дробь \( \displaystyle \frac<1><3>\). Что у тебя получилось?
Чтобы не повторять число \( 3\) много много раз, решили говорить «ноль целых и три в периоде», так как тройка будет повторяться после запятой бесконечное число раз. Из этого умозаключения следует определение:
Дробь называется периодической, если её последовательность цифр после запятой, начиная с некоторого места, представляет собой периодически повторяющуюся группу цифр.
Чтобы кратко записать такую дробь, период (повторяющиеся цифры после запятой) пишут в скобках:
\( \displaystyle \frac<1><3>=0,\underbrace<3>_<период>33333333….=0,\left( 3 \right)\)
\( \displaystyle \frac<1><7>=0,\underbrace<142857>_<<период>>\underbrace<142857>_<период>142…=0,\left( 142857 \right)\)
Важно, что период не может начинаться слева от запятой:
\( \displaystyle \frac<100><7>=\underbrace<14,2857>_<не период>1428571428571…=14,\left( 285714 \right)\).