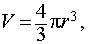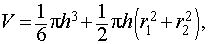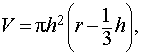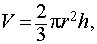Как называется часть сферы отсекаемая плоскостью
Сфера и шар. Площади сферы и ее частей. Объемы шара и его частей
Шар, сфера и их части
Введем следующие определения, связанные с шаром, сферой и их частями.
Определение 1. Сферой с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O равно r (рис. 1).
Определение 2. Шаром с центром в точке O и радиусом r называют множество точек, расстояние от которых до точки O не превосходит r (рис. 1).
Таким образом, сфера с центром в точке O и радиусом r является поверхностью шара с центром в точке O и радиусом r.
Замечание. Радиусом сферы ( радиусом шара ) называют отрезок, соединяющий любую точку сферы с центром сферы. Длину этого отрезка также часто называют радиусом сферы ( радиусом шара ).
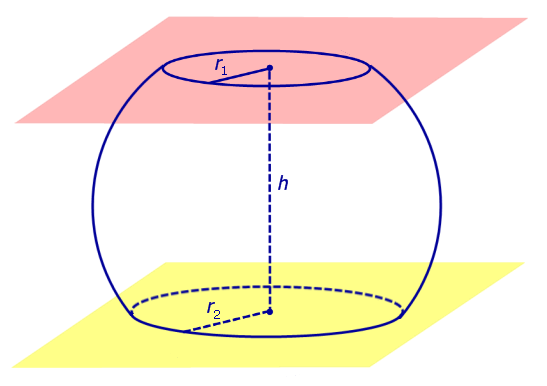
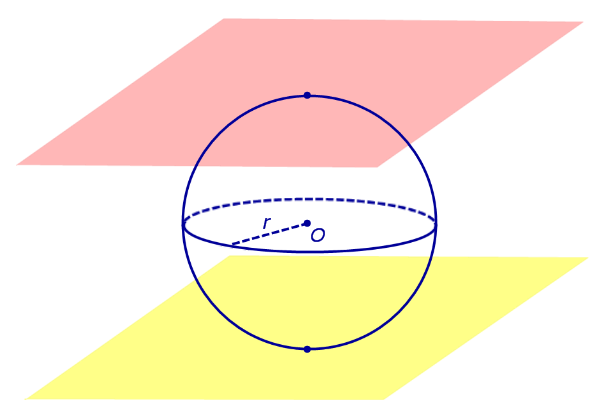
Определение 3. Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Определение 4. Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями параллельными плоскостями (рис. 2).
Окружности, ограничивающие сферический пояс, называют основаниями сферического пояса.
Расстояние между плоскостями Расстояние между плоскостями оснований сферического пояса называют высотой сферического пояса.
Из определений 3 и 4 следует, что шаровой слой ограничен сферическим поясом и двумя кругами, плоскости которых параллельны параллельны между собой. Эти круги называют основаниями шарового слоя.
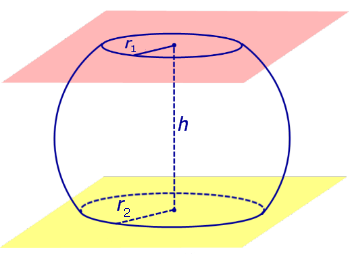
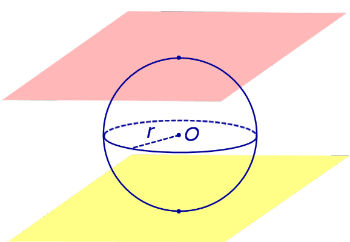
Определение 5. Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость (рис. 3).
Определение 6. Шаровым сегментом называют каждую из двух частей, на которые делит шар пересекающая ее плоскость (рис. 3).
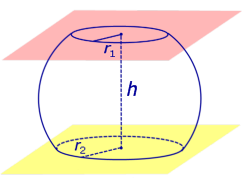
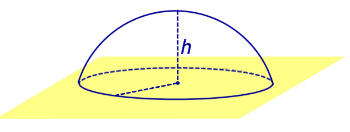
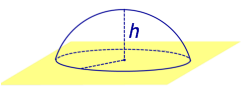
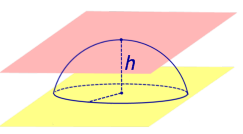
Из определений 3 и 5 следут, что сферический сегмент представляет собой сферический пояс, у которого одна из плоскостей оснований касается сферы (рис. 4). Высоту такого сферического пояса и называют высотой сферического сегмента.
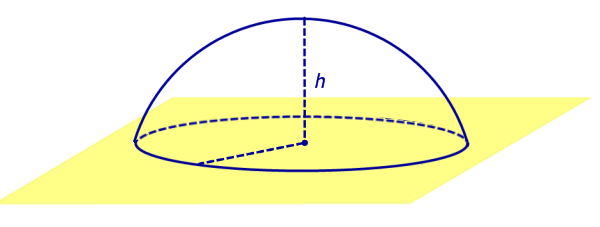
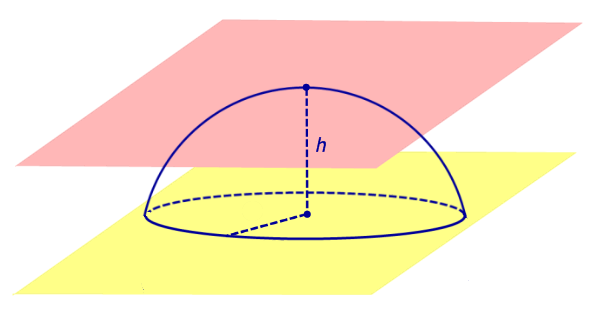
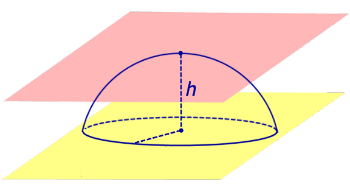
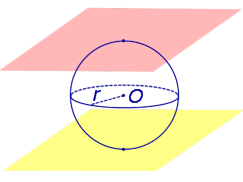
По той же причине всю сферу можно рассматривать как сферический пояс, у которого обе плоскости оснований касаются сферы (рис. 5). Соответственно, весь шар – это шаровой слой, у которого обе плоскости оснований касаются шара (рис. 5).
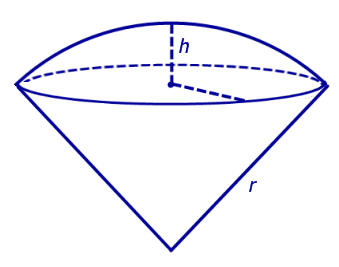
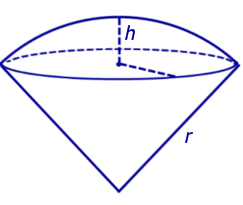
Определение 7. Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы (рис. 6).
Площади сферы и ее частей. Объемы шара и его частей
В следующей таблице приведены формулы, позволяющие вычислить объем шара и объемы его частей, а также площадь сферы и площади ее частей.
| Фигура | Рисунок | Формула | Описание |
| Сфера |  | Объем шарового сектора |
где
r – радиус сферы.
где
r – радиус шара.
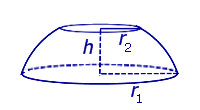
Площадь сферического пояса:
Нахождение площади шарового сегмента
В данной публикации мы рассмотрим формулы, с помощью которых можно вычислить площадь поверхности сегмента шара, а также разберем пример решения задачи для демонстрации их практического применения.
Определение сегмента шара
Сегмент шара (или шаровый сегмент) – это часть шара, отсеченная плоскостью. На чертеже ниже закрашен зеленым цветом.
Связь между радиусом основания сегмента, его высотой и радиусом шара:
Формулы для нахождения площади сегмента шара
Площадь основания
Основанием шарового сегмента является круг, площадь (S) которого находится по стандартной формуле (в расчетах число π округляется до 3,14):
Примечание: если известен диаметр круга (d), чтобы найти радиус (r), нужно первое разделить на второе, то есть:
Площадь сферической поверхности
Чтобы найти площадь (S) сферической/внешней поверхности шарового сегмента, необходимо знать его высоту и радиус самого шара.
Площадь полной поверхности
Чтобы найти площадь (S) полной поверхности сегмента шара, необходимо сложить площади его основания и внешней поверхности.
Пример задачи
Дан шар радиусом 6 см. Найдите полную площадь шарового сегмента, если известно, что его высота равняется 2,4 см, а радиус основания –
Решение
Воспользуемся формулами, приведенными выше, подставив в них известные по условиям задачи значения.
Sсфер. пов. = 2 ⋅ 3,14 ⋅ 6 см⋅ 2,4 см =
Sполн. = Sосн. + Sсфер. пов. = 69,3626 см 2 + 90,432 см 2 =
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №14. Объем шара и его частей
Перечень вопросов, рассматриваемых в теме
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.
Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.
Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.
Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями
Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями
Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы
Объем шара равен 
.
Объем шарового сегмента равен 
.
Объем шарового сектора равен 
.
Объем шарового слоя равен 
.
Примеры и разбор решения заданий тренировочного модуля
№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.
№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.
Решение: запишем формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна 
.
Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле 
. Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен 
(см), радиус второго основания равен 
(см).
Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен 
.
Как называется часть сферы отсекаемая плоскостью
Рассмотрим плоскость, проходящую на расстоянии, меньшем радиуса, от центра шара. Эта плоскость разбивает шар на два тела, каждое из которых называется шаровым сегментом. Круг, полученный в сечении шара рассматриваемой плоскостью, называется основанием шарового сегмента. Шаровой сегмент можно рассматривать как тело, полученное вращением кругового сегмента, относительно прямой, содержащей диаметр круга, перпендикулярный хорде кругового сегмента.
Часть шара, заключенная между двумя параллельными секущими плоскостями, называется шаровым слоем.
Математически верное определение
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью. Секущая плоскость, проходящая через точку 
(лежащую внутри шара), разделяет шар на два шаровых сегмента. Круг, получившийся в сечении, называется основанием каждого из этих сегментов, а длины отрезков 
и 
диаметра 
(проходящего через точку 
), перпендикулярного к секущей плоскости, называются высотами сегментов.
Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 
, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Истроическая справка
Определения из учебников
Шаровым сектором назывется тело, которое получатся из шарового сегмента и конуса следующим образом. В случае, когда сегмент меньше полушара, шаровой сектор получается дополнением этого сегмента конусом с тем же основанием, которое у сегмента, и вершиной в центре шара. В случае сегмента, большего полушара, шаровой сектор получается из этого сегмента удалением из него конуса, у которого основанием служит основание сегмента, а вершина в центре шара.
Шаровым сектором называют фигуру, полученную при вращении кругового сектора вокруг оси, содержащей один из его граничных радиусов.
Шаровым сектором называется тело, полученное вращением кругового сектора с углом, меньшим 
, вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов.
Шаровым сегментом называется меньшая часть шара, отсекаемая от него какой-нибудь плоскостью, не проходящей через центр шара. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть радиуса шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента.
Шаровым поясом будем называть часть шара, заключенную между двумя параллельными секущими плоскостями. Сечения шара этими плоскостями называются основаниями шарового пояса, а расстояние между ними называется высотой шарового пояса.
Шаровым сегментом называется меньшая часть шара, отсекаемая от него какой-нибудь плоскостью, не проходящей через центр шара. Круг, образованный сечением шара этой плоскостью, называется основанием шарового сегмента. Часть радиуса шара, лежащая внутри шарового сегмента и перпендикулярная его основанию, называется высотой шарового сегмента.
Шаровым поясом будем называть часть шара, заключенную между двумя параллельными секущими плоскостями. Сечения шара этими плоскостями называются основаниями шарового пояса, а расстояние между ними называется высотой шарового пояса.
Перпендикуляр, проведенный из точки одного основания к плоскости другого, называется высотой шарового слоя (шарового пояса).
Сегментную поверхность и шаровой пояс можно рассматривать как поверхности вращения: в то время, как при вращении полуокружности вокруг диаметра 
образуется шаровая поверхность (сфера), при вращении дуги 
этой полуокружности вокруг того же диаметра образуется сегментная поверхность, а при вращении дуги 
— шаровой пояс.
Тело, образованное при вращении кругового сектора с углом 
(
) вокруг прямой, которая содержит диаметр круга, не имеющий с круговым сектором общих внутренних точек, называется шаровым сектором.
Из этого определения следует, что поверхность шарового сектора состоит из сегментной поверхности и боковой поверхности конуса или из поверхности шарового пояса и боковых поверхностей двух конусов.
Шаровой пояс и сегментную поверхность можно рассматривать как поверхность вращения, в то время как полуокружность, вращаясь вокруг диаметра 
, описывает шаровую поверхность, часть ее 
описывает пояс, а часть 
— сегментную поверхность.
Тело, получаемое от вращения кругового сектора вокруг диаметра, не пересекающего ограничивающую его дугу, называется шаровым сектором. Это тело ограничено боковыми поверхностями двух конусов и поверхностью шарового пояса; последняя называется основанием шарового сектора.
Сравнения определений
В учебниках А.В.Погорелова и В.М.Клопского, З.А.Скопеца, М.И.Ягодовского угол в осевом сечении шарового сектора божет быть больше 
. В остальных из рассматриваемых здесь учебниках этот угол меньше 
.
В учебниках А.П.Киселева и Е. В. Потоскуева, Л. И. Звавича в определении шарового сектора ось вращения шарового сектора не обязана содержать радиус кругового сектора.
Геометрия. 11 класс
Конспект урока
Геометрия, 11 класс
Урок №14. Объем шара и его частей
Перечень вопросов, рассматриваемых в теме
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. и др. Геометрия 10-11 учебник для общеобразов. учрежд.: база и профильн. М: Просвещение.2009
Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Геометрия. 10–11 классы : учеб. для общеобразоват. организаций : базовый и углубл. уровни и др. – М.: Просвещение, 2014. – 255, сс. 121-126.
Шарыгин И.Ф. Геометрия. 10–11 кл. : учеб. для общеобразоват. учреждений – М.: Дрофа, 2009. – 235, : ил., ISBN 978–5–358–05346–5, сс. 178-196.
Потоскуев Е.В., Звавич Л.И. Геометрия. 11кл.: учеб. Для классов с углубл. И профильным изучением математики общеобразоват. Учреждений – М.: Дрофа, 2004. – 368 с.: ил., ISBN 5–7107–8310–2, сс. 5-30.
Открытые электронные ресурсы:
Теоретический материал для самостоятельного изучения
Шаром называется множество всех точек пространства, находящихся от данной точки на расстоянии, не больше данного R.
Радиусом шара называют всякий отрезок, соединяющий центр шара с точкой шаровой поверхности.
Отрезок, соединяющий две точки шаровой поверхности и проходящий через центр шара, называется диаметром шара.
Концы любого диаметра шара называются диаметрально противоположными точками шара. Отрезок, соединяющий две любые точки шаровой поверхности и не являющийся диаметром шара, называют хордой шара.
Сферическим поясом (шаровым поясом) называют часть сферы, заключенную между двумя параллельными плоскостями
Шаровым слоем называют часть шара, заключенную между двумя параллельными плоскостями
Сферическим сегментом называют каждую из двух частей, на которые делит сферу пересекающая ее плоскость.
Шаровым сегментом называется часть шара, отсекаемая от него какой-нибудь плоскостью.
Шаровым сектором называют фигуру, состоящую из всех отрезков, соединяющих точки сферического сегмента с центром сферы
Объем шара равен .
Объем шарового сегмента равен .
Объем шарового сектора равен .
Объем шарового слоя равен .
Примеры и разбор решения заданий тренировочного модуля
№1. Круговой сектор радиуса R с центральным углом 60 градусов вращается вокруг одного из радиусов, образующих этот угол. Найдите объем тела вращения.
№2. Найдите объем шарового сектора, если радиус шара равен 6 см, а высота конуса, образующего сектор, составляет треть диаметра шара.
Решение: запишем формулу для вычисления объема шарового слоя.
Чтобы найти объём шарового слоя нам необходимо знать его высоту и радиусы двух его оснований.
По условию задачи нам дано расстояние между сечениями, как раз-таки это расстояние и есть высота данного шарового слоя, и она равна .
Теперь найдём чему равны радиусы оснований шарового слоя. Напомню, что сечением шара плоскостью является круг. Площадь круга вычисляется по формуле . Отсюда найдём радиусы оснований шарового слоя. Тогда имеем, радиус одного основания равен (см), радиус второго основания равен (см).
Подставим радиусы оснований и высоту шарового слоя в формулу его объёма. Посчитаем. Получаем, что объём данного шарового слоя равен .