что такое термодинамическая система в физике

Термодинамическая система

Термодинамика
Статья является частью одноименной серии.
Начала термодинамики
Уравнение состояния
Термодинамические величины
Термодинамические потенциалы
Термодинамические циклы
Фазовые переходы
править
См. также «Физический портал»

Термодинамическая система — это некая физическая система, состоящая из большого количества частиц, способная обмениваться с окружающей средой энергией и веществом. Также обычно полагается, что такая система подчиняется статистическим закономерностям. Для термодинамических систем справедливы законы термодинамики.

Описание

Для описания термодинамической системы вводят так называемые термодинамические величины — набор физических величин, значения которых определяют термодинамическое состояние системы. Примерами термодинамических величин являются:

Если термодинамическое состояние системы не меняется со временем, то говорят, что система находится в состоянии равновесия. Строго говоря, термодинамические величины, приведённые выше, могут быть определены только в состоянии термодинамического равновесия.

Классификация

Термодинамические системы подразделяются на однородные по составу (например, газ в сосуде) и неоднородные (вода и пар или смесь газов в сосуде).

Выделяют также изолированные системы, то есть системы, которые не обмениваются с окружающей средой ни энергией, ни веществом, и закрытые системы, которые обмениваются со средой только энергией, но не обмениваются веществом. Если же в системе происходят обменные процессы с окружающей средой, то её называют открытой.

Полезное

Смотреть что такое «Термодинамическая система» в других словарях:

ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА — совокупность макроскопич. тел, к рые могут взаимодействовать между собой и с др. телами (внеш. средой) обмениваться с ними энергией и в вом. Т. с. состоит из столь большого числа структурных ч ц (атомов, молекул), что её состояние можно… … Физическая энциклопедия

ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА — макроскопическое тело, выделенное из окружающей среды при помощи перегородок или оболочек (они могут быть также и мысленными, условными) и характеризующееся макроскопическими параметрами: объемом, температурой, давлением и др. Для этого… … Большой Энциклопедический словарь

термодинамическая система — термодинамическая система; система Совокупность тел, могущих энергетически взаимодействовать между собой и с другими телами и обмениваться с ними веществом … Политехнический терминологический толковый словарь

ТЕРМОДИНАМИЧЕСКАЯ СИСТЕМА — совокупность физ. тел, которые могут обмениваться между собой и с др. телами (внешней средой) энергией и веществом. Т. с. является любая система, состоящая из очень большого числа молекул, атомов, электронов и др. частиц, имеющих множество… … Большая политехническая энциклопедия

термодинамическая система — Тело (совокупность тел), способное (способных) обмениваться с другими телами (между собой) энергией и (или) веществом. [Сборник рекомендуемых терминов. Выпуск 103. Термодинамика. Академия наук СССР. Комитет научно технической терминологии. 1984 г … Справочник технического переводчика

термодинамическая система — – произвольно выбранная часть пространства, содержащая одно или несколько веществ и отделенная от внешней среды реальной или условной оболочкой. Общая химия : учебник / А. В. Жолнин [1] … Химические термины

термодинамическая система — [thermodynamic system] макроскопическое тело, отделенное от окружающей среды реальными или воображаемыми границами, которое можно охарактеризовать термодинамическими параметрами: объемом, температурой, давлением и др. Различают изолированные,… … Энциклопедический словарь по металлургии

термодинамическая система — макроскопическое тело, выделенное из окружающей среды при помощи перегородок или оболочек (они могут быть также и мысленными, условными), которое можно характеризовать макроскопическими параметрами: объёмом, температурой, давлением и др. Для… … Энциклопедический словарь

термодинамическая система — termodinaminė sistema statusas T sritis chemija apibrėžtis Kūnas (kūnų visuma), kurį nuo aplinkos skiria reali ar įsivaizduojama riba. atitikmenys: angl. thermodynamic system rus. термодинамическая система … Chemijos terminų aiškinamasis žodynas

термодинамическая система — termodinaminė sistema statusas T sritis fizika atitikmenys: angl. thermodynamic system vok. thermodynamisches System, n rus. термодинамическая система, f pranc. système thermodynamique, m … Fizikos terminų žodynas

Источник

Что такое термодинамическая система в физике

Термодина́мика (греч. θέρμη — «тепло», δύναμις — «сила») — раздел физики, изучающий соотношения и превращения теплоты и других форм энергии. Термодинамика — это феноменологическая наука, опирающаяся на обобщения опытных фактов. Она изучает макроскопические системы, состоящие из огромного числа частиц —термодинамические системы. Процессы, происходящие в таких системах, описываются макроскопическими величинами, такими как давление или температура, которые не применимы к отдельным молекулам и атомам.

Современная феноменологическая термодинамика является строгой теорией, развиваемой на основе нескольких постулатов. Однако обоснование этих постулатов и их связь со свойствами и законами взаимодействия частиц, из которых построены термодинамические системы, даётся статистической физикой. Статистическая физика позволяет выяснить также и границы применимости термодинамики.

Законы термодинамики носят общий характер и не зависят от конкретных деталей строения вещества на атомарном уровне. Поэтому термодинамика успешно применяется в широком круге вопросов науки и техники, таких как энергетика, двигатели, фазовые переходы,химические реакции, явления переноса и даже чёрные дыры. Термодинамика имеет важное значение для самых разных областей физики и химии, химической технологии, аэрокосмической техники, машиностроения, клеточной биологии, биомедицинской инженерии,материаловедения и находит своё применение даже в таких областях, как экономика.

Разделы термодинамики

Современную феноменологическую термодинамику принято делить на равновесную (или классическую) термодинамику, изучающую равновесные термодинамические системы и процессы в таких системах, и неравновесную термодинамику, изучающую неравновесные процессы в системах, в которых отклонение от термодинамического равновесия относительно невелико и ещё допускает термодинамическое описание.

В равновесной термодинамике вводятся такие переменные, как внутренняя энергия, температура, энтропия, химический потенциал. Все они носят название термодинамических параметров (величин). Классическая термодинамика изучает связи термодинамических параметров между собой и с физическими величинами, вводимыми в рассмотрение в других разделах физики, например, с гравитационным или электромагнитным полем, действующим на систему. Химические реакции и фазовые переходы также входят в предмет изучения классической термодинамики. Однако изучение термодинамических систем, в которых существенную роль играют химические превращения, составляет предмет химической термодинамики, а техническими приложениями занимается теплотехника.

В системах, не находящихся в состоянии термодинамического равновесия, например, в движущемся газе, может применяться приближение локального равновесия, в котором считается, что соотношения равновесной термодинамики выполняются локально в каждой точке системы. Однако в неравновесной термодинамике переменные рассматриваются как локальные не только в пространстве, но и во времени, то есть в её формулы время может входить в явном виде. Отметим, что посвящённая вопросам теплопроводности классическая работа Фурье «Аналитическая теория тепла» (1822) опередила не только появление неравновесной термодинамики, но и работу Карно «Размышления о движущей силе огня и о машинах, способных развивать эту силу» (1824), которую принято считать точкой отсчёта в истории классической термодинамики.

Классическая термодинамика включает в себя следующие разделы:

Кроме этого, современная термодинамика включает также следующие направления:

Основы термодинамики

Термодинамика изучает системы, состоящие из очень большого числа частиц. Описание таких систем методами классической механики не только не представляется возможным, но и фактически лишено смысла. Особенности термодинамического описания возникают вследствие того, что поведение больших ансамблей частиц подчиняется статистическим закономерностям и не может быть сведено к анализу детерминированной эволюции динамических систем. Однако исторически термодинамика развивалась без опоры на представления статистической теории, и основные положения термодинамики могут быть сформулированы на основе ограниченного числа постулатов, являющихся обобщениями опытных фактов. Число этих постулатов варьируется у разных авторов в соответствии с тем, как строится аксиоматика термодинамики, но традиционно считается, что можно выделить четыре начала термодинамики.

Основные понятия термодинамики

Термодинамические системы

Термодинамическое равновесие

Фундаментальным для классической термодинамики является понятие термодинамического равновесия, которое тоже плохо поддаётся логическому определению и формулируется как обобщение экспериментальных фактов. Утверждается, что любая замкнутая термодинамическая система, для которой внешние условия остаются неизменными, с течением времени переходит в равновесное состояние, в котором прекращаются все макроскопические процессы. При этом в системе на микроскопическом уровне могут происходить самые разные процессы, например, химические реакции, которые могут протекать и в прямом, и в обратном направлении, однако в среднем эти процессы компенсируют друг друга, и макроскопические параметры системы остаются неизменными, флуктуируя относительно равновесного значения. Флуктуации изучаются в статистической физике.

Термодинамические параметры

Термодинамика не рассматривает особенности строения тел на молекулярном уровне. Равновесные состояния термодинамических систем могут быть описаны с помощью небольшого числа макроскопических параметров, таких как температура, давление, плотность, концентрации компонентов и т. д., которые могут быть измерены макроскопическими приборами. Описанное таким образом состояние называется макроскопическим состоянием, и законы термодинамики позволяют установить связь между макроскопическими параметрами. Если параметр имеет одно и то же значение, не зависящее от размера любой выделенной части равновесной системы, то он называется неаддитивным или интенсивным, если же значение параметра пропорционально размеру части системы, то он называется аддитивным или экстенсивным. Давление и температура — неаддитивные параметры, а внутренняя энергия и энтропия — аддитивные параметры.

Макроскопические параметры могут подразделяться на внутренние, характеризующие состояние системы как таковой, и внешние, описывающие взаимодействие системы с окружающей средой и силовыми полями, воздействующими на систему, однако это разделение достаточно условно. Так, если газ заключен в сосуд с подвижными стенками и его объём определяется положением стенок, то объём является внешним параметром, а давление газа зависит от скоростей теплового движения молекул и является внутренним параметром. Напротив, если задаётся внешнее давление, то его можно считать внешним параметром, а объём газа — внутренним параметром. Постулируется, что в состоянии термодинамического равновесия каждый внутренний параметр может быть выражен через внешние параметры и температуру системы. Такая функциональная связь называется обобщённым уравнением состояния системы.

Термодинамические процессы

Начала термодинамики

Нулевое начало термодинамики

Нулевое начало термодинамики названо так потому, что оно было сформулировано уже после того, как первое и второе начало вошли в число устоявшихся научных понятий. Оно утверждает, что изолированная термодинамическая система с течением времени самопроизвольно переходит в состояние термодинамического равновесия и остаётся в нём сколь угодно долго, если внешние условия сохраняются неизменными. Оно также называется общим началом. Термодинамическое равновесие предполагает наличие в системе механического, теплового и химического равновесия, а также равновесия фаз. Классическая термодинамика постулирует лишь существование состояния термодинамического равновесия, но ничего не говорит о времени его достижения.

В литературе в нулевое начало также часто включают положения о свойствах теплового равновесия. Тепловое равновесие может существовать между системами, разделёнными неподвижной теплопроницаемой перегородкой, то есть перегородкой, позволяющей системам обмениваться внутренней энергией, но не пропускающей вещество. Постулат о транзитивности теплового равновесия утверждает, что если два тела, разделённые такой перегородкой (диатермической), находятся в тепловом равновесии между собой, то любое третье тело, находящееся в тепловом равновесии с одним из этих тел, будет находиться также и в тепловом равновесии с другим телом.

Иначе говоря, если две замкнутые системы A и B приведены в тепловой контакт друг с другом, то после достижения термодинамического равновесия полной системой A+B системы Aи B будут находиться в состоянии теплового равновесия друг с другом. При этом каждая из систем A и B сама по себе также находится в состоянии термодинамического равновесия. Тогда если системы B и C находятся в тепловом равновесии, то системы A и C также находятся в тепловом равновесии между собой.

В иноязычной и переводной литературе часто нулевым началом называют сам постулат о транзитивности теплового равновесия, а положение о достижении термодинамического равновесия могут называть «минус первым» началом. Важность постулата о транзитивности состоит в том, что он позволяет ввести некоторую функцию состояния системы, обладающую свойствами эмпирической температуры, то есть создавать приборы для измерения температуры. Равенство эмпирических температур, измеренных с помощью такого прибора — термометра, есть условие теплового равновесия систем (или частей одной и той же системы).

Первое начало термодинамики

Первое начало термодинамики выражает универсальный закон сохранения энергии применительно к задачам термодинамики и исключает возможность создания вечного двигателяпервого рода, то есть устройства, способного совершать работу без соответствующих затрат энергии.

Внутреннюю энергию U термодинамической системы можно изменить двумя способами, совершая над ней работу или посредством теплообмена с окружающей средой. Первое начало термодинамики утверждает, что теплота, полученная системой, идёт на увеличение внутренней энергии системы и на совершение этой системой работы, что можно записать как δQ = δA + dU. Здесь dU — полный дифференциал внутренней энергии системы, δQ — элементарное количество теплоты, переданное системе, а δA — бесконечно малая или элементарнаяработа, совершённая системой. Так как работа и теплота не являются функциями состояния, а зависят от способа перехода системы из одного состояния в другое, применяется запись с символом δ, чтобы подчеркнуть, что δQ и δA — это бесконечно малые величины, которые нельзя считать дифференциалами какой-либо функции.

Знаки при δQ и δA в приведённом выше соотношении выражают соглашение о том, что положительной считают работу, совершаемую системой, и теплоту, получаемую системой, принятое в большинстве современных работ по термодинамике.

Работу, связанную с изменением количества вещества в системе (химическую работу), могут выделять из общего выражения для работы в отдельное слагаемое.

Второе начало термодинамики

Второе начало термодинамики задаёт ограничения на направление процессов, которые могут происходить в термодинамических системах, и исключает возможность создания вечного двигателя второго рода. Фактически к этому результату пришёл уже Сади Карно в сочинении «О движущей силе огня и о машинах, способных развивать эту силу». Однако Карно опирался на представления теории теплорода и не дал ясной формулировки второго начала термодинамики. Это было сделано в 1850—1851 годах независимо Клаузиусом иКельвином. Имеется несколько различных, но в то же время эквивалентных формулировок этого закона.

Постулат Кельвина: «Невозможен круговой процесс, единственным результатом которого было бы производство работы за счёт охлаждения теплового резервуара». Такой круговой процесс называется процессом Томсона-Планка, и постулируется, что такой процесс невозможен.

Постулат Клаузиуса: «Теплота не может самопроизвольно переходить от тела менее нагретого к телу более нагретому». Процесс, при котором не происходит никаких других изменений, кроме передачи теплоты от холодного тела к горячему, называется процессом Клаузиуса. Постулат утверждает, что такой процесс невозможен. Теплота может переходить самопроизвольно только в одном направлении, от более нагретого тела к менее нагретому, и такой процесс является необратимым.

Приняв за постулат невозможность процесса Томсона-Планка, можно доказать, что процесс Клаузиуса невозможен, и наоборот, из невозможности процесса Клаузиуса следует, что процесс Томсона-Планка также невозможен.

Третье начало термодинамики

Нулевые значения температуры и энтропии при абсолютном нуле приняты как удобные соглашения для устранения неоднозначности в построении шкалы для термодинамических величин. Нулевое значение температуры служит реперной точкой для построения термодинамической шкалы температур. Энтропия, обращающаяся в ноль при абсолютном нуле температуры, называется абсолютной энтропией. В справочниках термодинамических величин часто приводятся значения абсолютной энтропии при температуре 298,15 К, которые соответствуют увеличению энтропии при нагреве вещества от 0 К до 298,15 К.

Термодинамическое состояние

Динамическое, микро- и макросостояние

Моделирование всякой физической системы подразумевает указание полного набора параметров, необходимого для описания всех её возможных состояний и наблюдаемых величин. Описание термодинамических систем, состоящих из огромного числа частиц, варьируется в зависимости от того, какая степень детализации принимается для выбора набора параметров. Наиболее подробное описание в классической механике требует указания координат и импульсов всех частиц системы в какой-либо начальный момент времени и законов взаимодействия частиц, определяющих их эволюцию во времени. Описанное таким образом состояние системы называется динамическим. Для практических целей динамическое описание систем большого числа частиц непригодно. Следующим, более огрубленным уровнем описания является статистическое описание, когда динамические состояния усредняются по ячейкам фазового пространства в классической механике. В квантовой механике состояния различаются набором квантовых чисел и могут усредняться, например, по небольшим интервалам на шкале энергии. Такие состояния называются микросостояниями и изучаются в классической или квантовой статистической механике. Выбор способа описания системы зависит от характерных временных масштабов, на которых изучается эволюция системы.

Термодинамика имеет дело с макросостояниями, наиболее общим уровнем описания, где для указания состояния системы требуется минимальное число макроскопических параметров. Вообще говоря, проблема определения микро- и макросостояний и описания их статистических свойств относится к наиболее фундаментальным и пока не получившим окончательного решения вопросам статистической физики.

Функции состояния и уравнение состояния

При описании макросостояний используются функции состояния — это функции, однозначно определённые в состоянии термодинамического равновесия и не зависящие от предыстории системы и способа её перехода в равновесное состояние. Важнейшими функциями состояния при аксиоматическом построении термодинамики являются температура, внутренняя энергия и энтропия, вводимые в началах термодинамики, а также термодинамические потенциалы. Однако функции состояния не являются независимыми, и для однородной изотропной системы любая термодинамическая функция может быть записана как функция двух независимых переменных. Такие функциональные связи называются уравнениями состояния. Различают термическое уравнение состояние, выражающее связь между температурой, давлением и объёмом (или, что тоже самое, плотностью), калорическое уравнение состояние, выражающее внутреннюю энергию как функцию от температуры и объёма, и каноническое уравнение состояние, записываемое как термодинамический потенциал в соответствующих естественных переменных, из которого можно получить и термическое, и калорическое уравнения состояния. Знание уравнения состояния необходимо для применения общих принципов термодинамики к конкретным системам. Для каждой конкретной термодинамической системы её уравнение состояния определяется из опыта или методами статистической механики, и в рамках термодинамики оно считается заданным при определении системы.

Термическое уравнение состояния

Для многокомпонентной системы число термических уравнений состояния равно числу компонентов, например, для смеси идеальных газов эти уравнения состояния выглядят как p iV = ν iRT, где ν i — число молей i-го компонента смеси. Общее давление при этом будет равно сумме парциальных давлений компонентов, p=Σp i. Это соотношение называется законом Дальтона.

Термическое уравнение состояния фотонного газа устанавливает зависимость давления электромагнитного излучения от температуры и не содержит других переменных.

Для пространственно однородного элемента упругой среды при его продольной деформации примером термического уравнения состояния служит закон Гука; в термодинамике деформируемого твёрдого тела термические уравнения состояния, связывающие температуру и компоненты тензоров напряжений и деформаций, входят в число определяющих уравнений; для магнитных сред используют магнитное уравнение состояния M = M(H,T), примером которого может служить закон Кюри; для диэлектриков уравнение состояния имеет вид P = P(E,T); здесь M — магнитный момент вещества, H — напряжённость магнитного поля, P — поляризация, E — напряжённость электрического поля.

Существование термического уравнения состояния вытекает из закона транзитивности термического равновесия, однако сама термодинамика ничего не говорит относительно вида функциональной зависимости между входящими в это уравнение переменными, за исключением того, что уравнение состояния должно удовлетворять определённым условиям устойчивости.

Основные формулы термодинамики

Условные обозначения

[42]Изохорно-изотермический потенциал (свободная энергия Гельмгольца)ДжИзобарно-изотермический потенциал (свободная энергия Гиббса, свободная энтальпия)ДжРабота, совершённая газомДжТепло, переданное газуДжМолярная теплоёмкость газа при постоянном давленииДж/(К·моль)Молярная теплоёмкость газа при постоянном объёмеДж/(К·моль)Удельная теплоёмкостьДж/(К·кг)Показатель адиабаты—

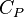
Формулы термодинамики идеального газа

Уравнение состояния идеального газа (уравнение Клапейрона—Менделеева)
Изменение внутренней энергии газа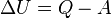
Работа газа
Средняя энергия молекулы газа
Средняя кинетическая энергия молекулы газа: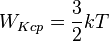
Внутренняя энергия газа

Теплоёмкость газа при постоянном объёмеТеплоёмкость газа при постоянном давлении

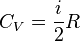
Выражение основных величин через термодинамические потенциалы

Все термодинамические потенциалы имеют свои канонические наборы переменных и используются для анализа процессов при соответствующих условиях. Так, для изотермических изохорических процессов () удобно использовать , для изотермических изобарических () — , а для изолированных систем () — .

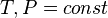
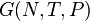
S(N,U,V) (энтропия)

F(N,T,V) (свободная энергия Гельмгольца)

G(N,T,P) (энергия Гиббса)

U(N,S,V) (внутренняя энергия)

Уравнение Гиббса и уравнение Гиббса—Дюгема

Выражение для полного дифференциала внутренней энергии называется фундаментальным уравнением Гиббса или просто уравнением Гиббса:

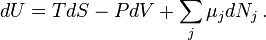
Значимость этого уравнения (и его более общих вариантов) состоит в том, что оно представляет собой тот фундамент, на котором базируется весь математический аппарат современной феноменологической термодинамики, как равновесной, так и неравновесной. По большому счёту, рассмотренные выше законы (начала) термодинамики нужны были именно для обоснования этого соотношения. Всю аксиоматику равновесной термодинамики можно свести к постулированию самого этого уравнения и свойств входящих в него термодинамических переменных.

С использованием других термодинамических потенциалов уравнение Гиббса можно переписать в следующих эквивалентных формах:

Среди термодинамических величин выделяют экстенсивные (внутренняя энергия, энтропия, объём и др.) и интенсивные (давление, температура и др.) величины. Величина называется экстенсивной, если ее значение для системы, сложенной из нескольких частей, равно сумме значений этой величины для каждой части. Предположением об экстенсивности термодинамических величин, однако, можно пользоваться, если рассматриваемые системы достаточно большие и можно пренебречь различными краевыми эффектами при соединении нескольких систем, например, энергией поверхностного натяжения. Пусть U (экстенсивная величина) является однородной функцией первого порядка от своих экстенсивных аргументов (математическое выражение аксиомы экстенсивности): для любого 0″ src=»http://upload.wikimedia.org/math/7/c/5/7c51dee4cd461ebcbbecf8fcee8d236a.png» style=»border:none;vertical-align:middle;margin:0px» />

Для любой дифференцируемой однородной функции первого порядка выполняется теорема Эйлера:

Для энергии теорема Эйлера имеет вид:

Отсюда легко следует уравнение Гиббса — Дюгема:

Это уравнение показывает, что между интенсивными переменными существует одна связь, являющаяся следствием предположения об аддитивности свойств системы. В частности, непосредственным следствием соотношений Гиббса-Дюгема является выражение для термодинамического потенциала Гиббса через химические потенциалы компонент смеси:

Термодинамика сплошных сред

Приведённые выше формулировки аксиом термодинамики и соотношения для термодинамических потенциалов имеют место для простых систем — изотропных сред. Для более сложных сред — анизотропных жидкостей и твёрдых тел, сред с электромагнитными свойствами и других, законы термодинамики имеют более сложную формулировку, а термодинамические потенциалы формулируются в обобщенном виде с использованием тензоров. В физике сплошных сред (физике континуума) термодинамика рассматривается как её составная часть, вводящая в рассмотрение переменные, характеризующие тепловые (термические) и химические свойства среды, и их связь с другими физическими величинами, а аксиомы термодинамики включаются в общую систему аксиом.

Источник