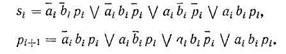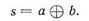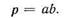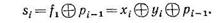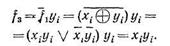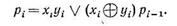алгоритм преобразования двоично десятичного кода в двоичный код
Преобразование двоично-десятичного кода в двоичный
Во многих случаях двоично-десятичный код можно достаточно просто получить непосредственно, например с помощью двоично-десятичных счетчиков. Как будет показано ниже, в двоично-десятичном коде также можно выполнять многие вычислительные операции. Однако в некоторых случаях необходимо все же провести преобразование его в двоичный код.
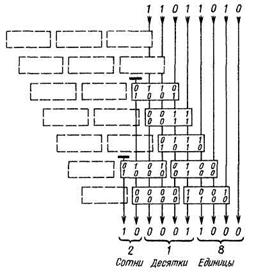
Рис. 7. Преобразование двоичного кода в двоично-десятичный
с помощью комбинационной схемы. Приведенные значения соответствуют
преобразованию числа 218.
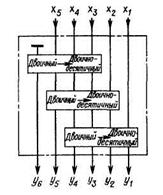
Рис. 8. Структура интегральной микросхемы для преобразования
двоичного кода в двоично-десятичный SN 74185.
Это можно сделать путем последовательного деления числа на 2. Для этого десятичное число делится на 2. Если оно нечетное, то в остатке получится 1, т.е. в разряде 2° записывается 1. Затем частное от деления еще раз делится на 2, и, если остаток равен нулю, в разряде 2 1 записывается 0. Если остаток равен 1, то в этом разряде записывается 1. Аналогично получают и более старшие разряды двоичного числа. Деление двоично-десятичного числа на 2 очень просто можно провести путем сдвига вправо на один разряд, так как отдельные цифры уже представлены в двоичном коде. Самый правый бит, выдвинутый из двоично-десятичной разрядной сетки, и является искомым значением разряда. Но если при сдвиге единица пересекает границу между декадами, то возникает ошибка: при переходе от десятков к единицам значение разряда должно уменьшиться наполовину от десяти до пяти. Однако в случае двоичного числа эта величина становится равной восьми. Поэтому, для коррекции нужно вычесть 3. Из этого вытекает следующее правило коррекции: если старший разряд в декаде равен единице, то необходимо данную декаду уменьшить на три. Таким образом, можно непосредственно составить таблицу переключений для корректирующего элемента 3. Процесс преобразования заканчивается, если все двоично-десятичное число будет выдвинуто из разрядной сетки.
На рис. 9 приведена комбинационная схема для преобразования 272-разрядного двоично-десятичного числа. Здесь, так же как и в схеме на рис. 7, сдвиг двоично-десятичных разрядов достигается путем соответствующего соединения одинаковых комбинационных схем. Чтобы наглядно продемонстрировать структуру этой
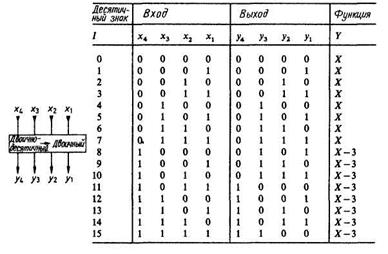
Таблица 3.Таблица переключений корректирующего элемента
для преобразования двоично-десятичного кода в двоичный
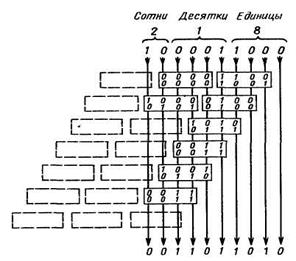
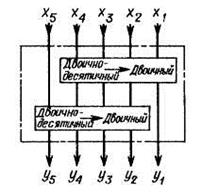
Рис. 9. Преобразование двоично-десятичного кода в двоичный с помощью комбинационной схемы. Приведенные значения соответствуют преобразованию числа 218.
схемы, на рис. 9. изображены все три корректирующих элемента для каждой ступени кодопреобразователя. В действительности если старший разряд корректирующего элемента не используется, то, согласно табл. 3, коррекция не нужна и данный элемент можно исключить. На рис. 9 такие элементы изображены пунктирной линией.
Рис. 10. Структура интегральной микросхемы для преобразования
двоично-десятичного кода в двоичный.
Корректирующие схемы составляются из отдельных секций, содержащих по два элемента (рис. 10). Каждая секция представляет собой одну интегральную микросхему ПЗУ на 32 байта, программируемую изготовителем. Такая микросхема (типа SN 74184) имеет пять входов и пять выходов.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования», стр: 64-67.
2. У. Титце, К. Шенк «Полупроводниковая схемотехника», стр: 321-325.
3. Э.В. Евреинов «Цифровая и вычислительная техника», стр: 74-76.
4. В.А. Скаржепа «Электроника и микросхемотехника» (сборник задач), стр: 122-127.
ЗАНЯТИЕ 1.1.10 Назначение сумматоров. Комбинационные сумматоры. Синтез
одноразрядного комбинационного сумматора.
ВОПРОСЫ ЗАНЯТИЯ:
1. Назначение и классификация сумматоров.
2. Комбинационные сумматоры. Синтез одноразрядного комбинационного сумматора.
ПЕРВЫЙ ВОПРОС
Сумматор – электронный узел, выполняющий операцию суммирования цифровых кодов двух чисел. При сложении двух чисел, представленных в виде двоичных кодов, происходит сложение этих чисел в данном i-м разряде и прибавление единицы переноса (если она возникает) из младшего (i—1)-го разряда.
По принятой системе счисления и кодирования различают сумматоры двоичные, троичные, десятичные, двоично-десятичные и др.
По способу организации суммирования сумматоры могут быть комбинационные и накапливающие.
Сумматор для сложения многоразрядных чисел представляет собой набор одноразрядных сумматоров, имеющих входы для слагаемых и переноса из младшего разряда и выходы суммы и переноса в старший разряд.
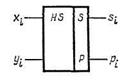
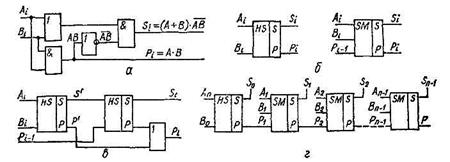
Рис. 1. Условное графическое Рис. 2. Условное графическое
обозначение полусумматора. обозначение одноразрядного сумматора.
По способу обработки многоразрядных чисел различают сумматоры последовательные, параллельные ипараллельно-последовательные.
Рассмотрим сложение двух целых двоичных чисел без знаков А и В с формированием их суммы S:
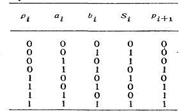
Из примера следует, что при формировании результата в любом i-м разряде необходимо учесть значения чисел в этом разряде аi и Ьi а также перенос в этот разряд из предыдущего разряда р.Формируются значение суммы в этом разряде si и перенос в следующий разряд pi+1. Сумматор может быть построен в виде комбинационного устройства, содержащего схемы для сложения отдельных разрядов (одноразрядные двоичные сумматоры). Условия функционирования одноразрядного двоичного сумматора определяются в табл. 1.
Булевы функции, описывающие работу одноразрядного двоичного сумматора, можно записать в виде
Используя различные варианты преобразования этих функций, можно реализовать большое число структур одноразрядных двоичных сумматоров.
ВТОРОЙ ВОПРОС
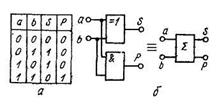
Суммирование двоичных чисел в вычислительных устройствах осуществляется комбинационными сумматорами. Одним из простейших суммирующих устройств является комбинационный одноразрядный суммирующий элемент, таблица истинности и схема которого показаны на рис. 1.
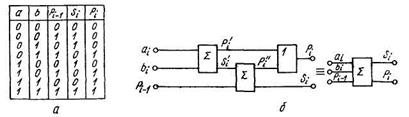
Рис.1 Таблица истинности (а) одноразрядного
комбинационного сумматора и его схема (б).
Устройство осуществляет суммирование двух одноразрядных двоичных чисел, сумма s которых также имеет один разряд. На выходе р устройства формируется сигнал переноса в следующий, более старший разряд, если оба суммируемых числа имеют единичные значения.
Нетрудно заметить, что функция s реализуется элементом неравнозначности (сумма по модулю 2):
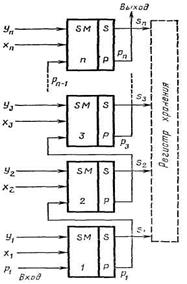
Функция переноса — это операция «И»:
На рис. 1, б показано условное обозначение данного элемента. Этот элемент называют иногда одноразрядным полусумматором, поскольку в нем не учитывается возможность суммирования сигнала переноса из предыдущего разряда.
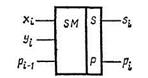
Два одноразрядных полусумматора образуют одноразрядный сумматор. Таблица истинности, схема и его условное обозначение показаны на рис. 2.
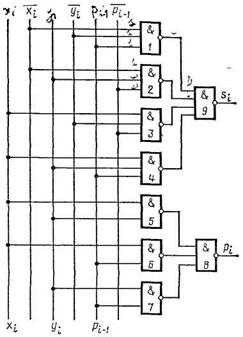
Рис. 2. Таблица истинности (а), схема (б) и условное
обозначение одноразрядного сумматора.
Промежуточная сумма s образуется в результате суммирования значений одноименных разрядов ai и bi исходных чисел Затем s суммируется с сигналом переноса рi-1 из предыдущего разряда и получается окончательное значение суммы si. Сигналы переносов 



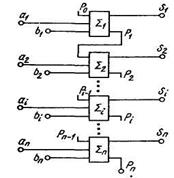
Рис. 3. Схема одноразрядного комбинационного сумматора
Рис. 3. Схема многоразрядного комбинационного сумматора.
Одноразрядный накапливающий сумматор.Это логическая схема, в которой исходные слова хi, уi, pi — 1 в виде входных сигналов поступают на вход поочередно и накапливаются и сохраняются на выходе после прекращения подачи сигналов. Схема накапливающего сумматора строится на основе триггера со счетным входом, реализующим операцию сложения по модулю 2.
Схема одноразрядного накапливающего сумматора приведена на рис. 4. В этой схеме после установки триггера в состояние 0 сигналы xi,yi, pi-1 поступают на элемент И – ИЛИ последовательно в моменты времени t1, t2, t3 соответственно.
В момент времени t1 поступает сигнал первого слагаемого хi ,который запоминается в триггере. Затем в момент времени t2 через И – ИЛИ на счетный вход триггера поступает сигнал второго слагаемого уi. При этом триггер реализует функцию si = fi(xi 
Сигнал переноса в старший разряд имеет две составляющие,
одна из которых вырабатывается схемой И1; peaлизующей переключательную функцию.Вторая составляющая вырабатывается в том случае, если хi и yi равны 1. Она реализуется схемой И2, на один из входов которой подается сигнал с инверсного выхода триггера, а на другой второе слагаемое yi,которое подается в дискретный момент времени t3. В этот момент времени в триггере хранится функция fi, поэтому элемент И2 реализует переключательную функцию
Таким образом, сигнал переноса на выходе схемы ИЛИ3 определяется выражением
Рис. 4. Схема одноразрядного накапливающего сумматора.
Основной недостаток накапливающего сумматора – малое быстродействие, поскольку в каждом цикле суммирования одного разряда двух слагаемых число срабатываний счетной схемы может быть равно трем.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 105-108.
2. Б.Я. Лихтциндер «Микропроцессоры и вычислительные устройства в радиотехнике» стр: 43-44.
ЗАНЯТИЕ 1.1.11 Комбинационные сумматоры последовательного и
ЗАНЯТИЕ 1.1.12 Основные характеристики надежности цифровых устройств.
Функции систем контроля и диагностирования.
ВОПРОСЫ ЗАНЯТИЯ:
1. Сумматоры последовательного и параллельного действия.
2. Основные характеристики надежности цифровых устройств.
3. Функции систем контроля и диагностирования.
ПЕРВЫЙ ВОПРОС
Последовательные сумматоры. Это одноразрядные сумматоры, в которых числа поступают на сложение последовательным кодом. Они преобразуют последовательные коды слагаемых, подаваемых на вход сумматора, в последовательный код суммы этих слагаемых.
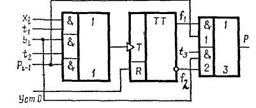
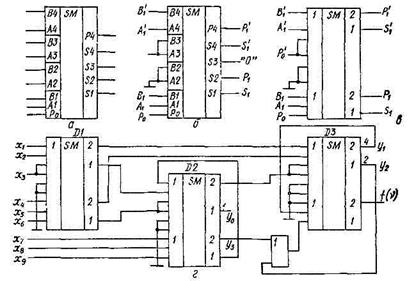
Рис. 1. Схема параллельного n-разрядного сумматора.
Быстродействие такого сумматора определяется временем суммирования в разряде сумматора tc и временем распространения переноса tp последовательно по всему n-разрядному сумматору, т. е. T=tc+(n—l)tp.
Для повышения быстродействия сумматоры выполняют с использованием схем с ускоренным распространением переносов (параллельным или групповым).
Для сложения n-разрядных чисел необходимо п – 1 одноразрядных полных сумматоров и один полусумматор в нулевом разряде (рис. 1, г).
В настоящее время в виде микросхем выпускаются одно-(165ИМ1), двух- (155ИМ2) и четырехразрядные (155ИМЗ, 564ИМ1) двоичные сумматоры. На рис 2, а показано условное графическое обозначение четырехразрядного двоичного сумматора. Входы At и В;, где t = 1, 2, 3, 4 и Ро логически равноценны.
ВТОРОЙ ВОПРОС
Под надёжностью изделия (элемента, узла, устройства, системы) понимают свойство последнего сохранять своё качество при определенных условиях эксплуатации в течении заданного промежутка времени, т.е. надежность – качество, развернутое во времени.
Изделия в процессе эксплуатации подразделяются по показателям надежности:
1. Невосстанавливаемые изделия – изделия, поведение которых существенно лишь до первого отказа. Характеризуются следующими показателями надёжности: интенсивностью отказов λ(t); частотой отказов f(t); вероятностью безотказной работы P(t); вероятностью отказа Q(t); наработкой на отказ То.
2. Восстанавливаемые изделия – изделия, эксплуатация которых допускает их многократный ремонт. Характеризуются следующими количественными показателями надежности: параметрами потока отказов ω(t) и потока восстановлений μ(t); функцией готовности Кг(t); коэффициентом готовности Кг; средним временем работы между двумя отказами tср; средним временем восстановления tв.
При анализе и сравнении качества изделий, при расчете надежности, при определении вероятности исправного действия системы и сроков ремонта, при определении запасов комплектующих изделий, а также при некоторых других технических и экономических расчетах необходима количественная оценка надежности.
Для удобства рассмотрения показатели надежности подразделяются на четыре группы.
Преобразование двоично-десятичного кода в двоичный.
Во многих случаях двоично-десятичный код можно достаточно просто получить непосредственно, например с помощью двоично-десятичных счетчиков. Как будет показано ниже, в двоично-десятичном коде также можно выполнять многие вычислительные операции. Однако в некоторых случаях необходимо все же провести преобразование его в двоичный код.
Рис. 7. Преобразование двоичного кода в двоично-десятичный
с помощью комбинационной схемы. Приведенные значения соответствуют
преобразованию числа 218.
Рис. 8. Структура интегральной микросхемы для преобразования
двоичного кода в двоично-десятичный SN 74185.
Это можно сделать путем последовательного деления числа на 2. Для этого десятичное число делится на 2. Если оно нечетное, то в остатке получится 1, т.е. в разряде 2° записывается 1. Затем частное от деления еще раз делится на 2, и, если остаток равен нулю, в разряде 2 1 записывается 0. Если остаток равен 1, то в этом разряде записывается 1. Аналогично получают и более старшие разряды двоичного числа. Деление двоично-десятичного числа на 2 очень просто можно провести путем сдвига вправо на один разряд, так как отдельные цифры уже представлены в двоичном коде. Самый правый бит, выдвинутый из двоично-десятичной разрядной сетки, и является искомым значением разряда. Но если при сдвиге единица пересекает границу между декадами, то возникает ошибка: при переходе от десятков к единицам значение разряда должно уменьшиться наполовину от десяти до пяти. Однако в случае двоичного числа эта величина становится равной восьми. Поэтому, для коррекции нужно вычесть 3. Из этого вытекает следующее правило коррекции: если старший разряд в декаде равен единице, то необходимо данную декаду уменьшить на три. Таким образом, можно непосредственно составить таблицу переключений для корректирующего элемента 3. Процесс преобразования заканчивается, если все двоично-десятичное число будет выдвинуто из разрядной сетки.
На рис. 9 приведена комбинационная схема для преобразования 272-разрядного двоично-десятичного числа. Здесь, так же как и в схеме на рис. 7, сдвиг двоично-десятичных разрядов достигается путем соответствующего соединения одинаковых комбинационных схем. Чтобы наглядно продемонстрировать структуру этой
Таблица 3.Таблица переключений корректирующего элемента
для преобразования двоично-десятичного кода в двоичный
Рис. 9. Преобразование двоично-десятичного кода в двоичный с помощью комбинационной схемы. Приведенные значения соответствуют преобразованию числа 218.
схемы, на рис. 9. изображены все три корректирующих элемента для каждой ступени кодопреобразователя. В действительности если старший разряд корректирующего элемента не используется, то, согласно табл. 3, коррекция не нужна и данный элемент можно исключить. На рис. 9 такие элементы изображены пунктирной линией.
Рис. 10. Структура интегральной микросхемы для преобразования
двоично-десятичного кода в двоичный.
Корректирующие схемы составляются из отдельных секций, содержащих по два элемента (рис. 10). Каждая секция представляет собой одну интегральную микросхему ПЗУ на 32 байта, программируемую изготовителем. Такая микросхема (типа SN 74184) имеет пять входов и пять выходов.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования», стр: 64-67.
2. У. Титце, К. Шенк «Полупроводниковая схемотехника», стр: 321-325.
3. Э.В. Евреинов «Цифровая и вычислительная техника», стр: 74-76.
4. В.А. Скаржепа «Электроника и микросхемотехника» (сборник задач), стр: 122-127.
ЗАНЯТИЕ 1.1.10 Назначение сумматоров. Комбинационные сумматоры. Синтез
одноразрядного комбинационного сумматора.
ВОПРОСЫ ЗАНЯТИЯ:
1. Назначение и классификация сумматоров.
2. Комбинационные сумматоры. Синтез одноразрядного комбинационного сумматора.
ПЕРВЫЙ ВОПРОС
Сумматор – электронный узел, выполняющий операцию суммирования цифровых кодов двух чисел. При сложении двух чисел, представленных в виде двоичных кодов, происходит сложение этих чисел в данном i-м разряде и прибавление единицы переноса (если она возникает) из младшего (i—1)-го разряда.
По принятой системе счисления и кодирования различают сумматоры двоичные, троичные, десятичные, двоично-десятичные и др.
По способу организации суммирования сумматоры могут быть комбинационные и накапливающие.
Сумматор для сложения многоразрядных чисел представляет собой набор одноразрядных сумматоров, имеющих входы для слагаемых и переноса из младшего разряда и выходы суммы и переноса в старший разряд.
Рис. 1. Условное графическое Рис. 2. Условное графическое
обозначение полусумматора. обозначение одноразрядного сумматора.
По способу обработки многоразрядных чисел различают сумматоры последовательные, параллельные ипараллельно-последовательные.
Рассмотрим сложение двух целых двоичных чисел без знаков А и В с формированием их суммы S:
Из примера следует, что при формировании результата в любом i-м разряде необходимо учесть значения чисел в этом разряде аi и Ьi а также перенос в этот разряд из предыдущего разряда р.Формируются значение суммы в этом разряде si и перенос в следующий разряд pi+1. Сумматор может быть построен в виде комбинационного устройства, содержащего схемы для сложения отдельных разрядов (одноразрядные двоичные сумматоры). Условия функционирования одноразрядного двоичного сумматора определяются в табл. 1.
Булевы функции, описывающие работу одноразрядного двоичного сумматора, можно записать в виде
Используя различные варианты преобразования этих функций, можно реализовать большое число структур одноразрядных двоичных сумматоров.
ВТОРОЙ ВОПРОС
Суммирование двоичных чисел в вычислительных устройствах осуществляется комбинационными сумматорами. Одним из простейших суммирующих устройств является комбинационный одноразрядный суммирующий элемент, таблица истинности и схема которого показаны на рис. 1.
Рис.1 Таблица истинности (а) одноразрядного
комбинационного сумматора и его схема (б).
Устройство осуществляет суммирование двух одноразрядных двоичных чисел, сумма s которых также имеет один разряд. На выходе р устройства формируется сигнал переноса в следующий, более старший разряд, если оба суммируемых числа имеют единичные значения.
Нетрудно заметить, что функция s реализуется элементом неравнозначности (сумма по модулю 2):
Функция переноса — это операция «И»:
На рис. 1, б показано условное обозначение данного элемента. Этот элемент называют иногда одноразрядным полусумматором, поскольку в нем не учитывается возможность суммирования сигнала переноса из предыдущего разряда.
Два одноразрядных полусумматора образуют одноразрядный сумматор. Таблица истинности, схема и его условное обозначение показаны на рис. 2.
Рис. 2. Таблица истинности (а), схема (б) и условное
обозначение одноразрядного сумматора.
Промежуточная сумма s образуется в результате суммирования значений одноименных разрядов ai и bi исходных чисел Затем s суммируется с сигналом переноса рi-1 из предыдущего разряда и получается окончательное значение суммы si. Сигналы переносов 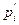
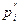
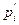
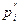
Рис. 3. Схема одноразрядного комбинационного сумматора
Рис. 3. Схема многоразрядного комбинационного сумматора.
Одноразрядный накапливающий сумматор.Это логическая схема, в которой исходные слова хi, уi, pi — 1 в виде входных сигналов поступают на вход поочередно и накапливаются и сохраняются на выходе после прекращения подачи сигналов. Схема накапливающего сумматора строится на основе триггера со счетным входом, реализующим операцию сложения по модулю 2.
Схема одноразрядного накапливающего сумматора приведена на рис. 4. В этой схеме после установки триггера в состояние 0 сигналы xi,yi, pi-1 поступают на элемент И – ИЛИ последовательно в моменты времени t1, t2, t3 соответственно.
В момент времени t1 поступает сигнал первого слагаемого хi ,который запоминается в триггере. Затем в момент времени t2 через И – ИЛИ на счетный вход триггера поступает сигнал второго слагаемого уi. При этом триггер реализует функцию si = fi(xi 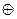
Сигнал переноса в старший разряд имеет две составляющие,
одна из которых вырабатывается схемой И1; peaлизующей переключательную функцию.Вторая составляющая вырабатывается в том случае, если хi и yi равны 1. Она реализуется схемой И2, на один из входов которой подается сигнал с инверсного выхода триггера, а на другой второе слагаемое yi,которое подается в дискретный момент времени t3. В этот момент времени в триггере хранится функция fi, поэтому элемент И2 реализует переключательную функцию
Таким образом, сигнал переноса на выходе схемы ИЛИ3 определяется выражением
Рис. 4. Схема одноразрядного накапливающего сумматора.
Основной недостаток накапливающего сумматора – малое быстродействие, поскольку в каждом цикле суммирования одного разряда двух слагаемых число срабатываний счетной схемы может быть равно трем.
Литература:
1. В.В. Стрыгин «Основы вычислительной, микропроцессорной техники и программирования» стр: 105-108.
2. Б.Я. Лихтциндер «Микропроцессоры и вычислительные устройства в радиотехнике» стр: 43-44.
ЗАНЯТИЕ 1.1.11 Комбинационные сумматоры последовательного и
ЗАНЯТИЕ 1.1.12 Основные характеристики надежности цифровых устройств.
Функции систем контроля и диагностирования.
ВОПРОСЫ ЗАНЯТИЯ:
1. Сумматоры последовательного и параллельного действия.
2. Основные характеристики надежности цифровых устройств.
3. Функции систем контроля и диагностирования.
ПЕРВЫЙ ВОПРОС
Последовательные сумматоры. Это одноразрядные сумматоры, в которых числа поступают на сложение последовательным кодом. Они преобразуют последовательные коды слагаемых, подаваемых на вход сумматора, в последовательный код суммы этих слагаемых.
Рис. 1. Схема параллельного n-разрядного сумматора.
Быстродействие такого сумматора определяется временем суммирования в разряде сумматора tc и временем распространения переноса tp последовательно по всему n-разрядному сумматору, т. е. T=tc+(n—l)tp.
Для повышения быстродействия сумматоры выполняют с использованием схем с ускоренным распространением переносов (параллельным или групповым).
Для сложения n-разрядных чисел необходимо п – 1 одноразрядных полных сумматоров и один полусумматор в нулевом разряде (рис. 1, г).
В настоящее время в виде микросхем выпускаются одно-(165ИМ1), двух- (155ИМ2) и четырехразрядные (155ИМЗ, 564ИМ1) двоичные сумматоры. На рис 2, а показано условное графическое обозначение четырехразрядного двоичного сумматора. Входы At и В;, где t = 1, 2, 3, 4 и Ро логически равноценны.
ВТОРОЙ ВОПРОС
Под надёжностью изделия (элемента, узла, устройства, системы) понимают свойство последнего сохранять своё качество при определенных условиях эксплуатации в течении заданного промежутка времени, т.е. надежность – качество, развернутое во времени.
Изделия в процессе эксплуатации подразделяются по показателям надежности:
1. Невосстанавливаемые изделия – изделия, поведение которых существенно лишь до первого отказа. Характеризуются следующими показателями надёжности: интенсивностью отказов λ(t); частотой отказов f(t); вероятностью безотказной работы P(t); вероятностью отказа Q(t); наработкой на отказ То.
2. Восстанавливаемые изделия – изделия, эксплуатация которых допускает их многократный ремонт. Характеризуются следующими количественными показателями надежности: параметрами потока отказов ω(t) и потока восстановлений μ(t); функцией готовности Кг(t); коэффициентом готовности Кг; средним временем работы между двумя отказами tср; средним временем восстановления tв.
При анализе и сравнении качества изделий, при расчете надежности, при определении вероятности исправного действия системы и сроков ремонта, при определении запасов комплектующих изделий, а также при некоторых других технических и экономических расчетах необходима количественная оценка надежности.
Для удобства рассмотрения показатели надежности подразделяются на четыре группы.
Дата добавления: 2015-12-08 ; просмотров: 3468 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ