записать в прямом обратном и дополнительном кодах
Записать в прямом обратном и дополнительном кодах
Арифметические операции на сумматорах прямого, обратного и дополнительного кода
Все операции в ЭВМ выполняют над числами, представленными специальными машинными кодами. Их использование позволяет обрабатывать знаковые разряды чисел так же, как и значащие разряды, а также заменять операцию вычитания операцией сложения.
Каждому двоичному числу можно поставить в соответствие несколько видов кодов.
Различают следующие коды двоичных чисел: прямой (П), обратный (ОК) и дополнительный (ДК).
Прямой код двоичного числа образуется из абсолютного значения этого числа и кода знака (0 или 1) перед его старшим числовым разрядом.
Прямой код двоичного числа образуется по следующему алгоритму:
1) определить данное двоичное число: либо целое (порядок), либо правильная дробь (мантисса);
2) если это дробь, то цифры после запятой можно рассматривать как целое число;
3) если это целое и положительное двоичное число, то вместе с добавлением нуля в старший разряд число превращается в код.
Для отрицательного двоичного числа перед ним ставится единица.
число Y 2 = +0,11011012 → код числа Y пр = 01101101.
Подчеркиванием выделяют знаковые разряды.
Обратный код двоичного числа образуется по следующему алгоритму:
1) обратный код положительных чисел совпадает с их прямым кодом;
2) обратный код отрицательного числа содержит единицу в знаковом разряде числа, а значащие разряды числа заменяются инверсными, т. е. нули заменяются единицами, а единицы нулями.
Свое название обратный код получил потому, что коды цифр отрицательного числа заменены инверсными.
Наиболее важные свойства обратного кода чисел:
— сложение положительного числа С с его отрицательным значением в обратном коде дает так называемую машинную единицу МЕок = 1|1111, состоящую из единиц в знаковом и в значащих разрядах числа;
— нуль в обратном коде имеет двоякое значение.
Он может быть как положительным числом 0|0000, так и отрицательным 1|1111.
Двойственное представление нуля явилось причиной того, что в современных ЭВМ все числа представляются не обратным, а дополнительным кодом.
Обратный код положительного двоичного числа совпадает с прямым кодом, а для отрицательного числа нужно, исключая знаковый разряд, во всех остальных разрядах нули заменить единицами и наоборот.
Дополнительный код положительных чисел совпадает с их прямым кодом. Дополнительный код отрицательного числа представляет собой результат суммирования обратного кода числа с единицей младшего разряда (2 0 – для целых чисел, 2 –k – для дробных).
Основные свойства дополнительного кода:
· сложение дополнительных кодов положительного числа С с его отрицательным значением дает так называемую машинную единицу дополнительного кода:
т. е. число 10 (два) в знаковых разрядах числа;
Дополнительный код положительного числа совпадает с его прямым кодом. Дополнительный код отрицательного числа образуется путем прибавления единицы к обратному коду.
Арифметические действия в машинных кодах
Сложение, а также вычитание чисел в обратном или дополнительном кодах выполняют с использованием обычного правила арифметического сложения многоразрядных чисел.
Это правило распространяется и на знаковые разряды чисел.
Различие обратного и дополнительного кодов связано с последующими действиями с единицей переноса из старшего разряда, изображающего знак числа.
При сложении чисел в обратном коде эту единицу надо прибавить к младшему разряду результата, а в дополнительном коде единица переноса из старшего разряда игнорируется, так как дополнительный код из обратного получается как раз прибавлением единицы.
Сложение и вычитание машинных чисел
Операция вычитания приводится к операции сложения путем преобразования чисел в обратный или дополнительный код согласно таблице.
Сложение (вычитание) машинных чисел
Скобки в представленных выражениях указывают на замену операции вычитания операцией сложения с обратным или дополнительным кодом соответствующего числа.
Сложение двоичных чисел осуществляется последовательно, поразрядно в соответствии с таблицей.
При выполнении сложения цифр необходимо соблюдать следующий алгоритм:
1) слагаемые должны иметь одинаковое число разрядов.
Для выравнивания разрядной сетки слагаемых можно дописывать незначащие нули слева к целой части числа и незначащие нули справа к дробной части числа;
2) знаковые разряды участвуют в сложении так же, как и значащие;
3) необходимые преобразования кодов производят с изменением знаков чисел. Приписанные незначащие нули изменяют свое значение при преобразованиях по общему правилу;
4) при преобразовании единицы переноса из старшего знакового разряда, в случае использования ОК, эта единица складывается с младшим числовым разрядом.
При использовании ДК единица переноса теряется. Знак результата формируется автоматически, результат представляется в том коде, в котором представлены исходные слагаемые.
1. Сложить два числа: А10 = 7, В10 = 16.
Исходные числа имеют различную разрядность, необходимо провести выравнивание разрядной сетки:
Сложение в обратном или дополнительном коде дает один и тот же результат:
2. Сложить два числа: А10 = +16, В10 = –7 в ОК и ДК.
По таблице необходимо преобразование А +(–В), в которой второй член преобразуется с учетом знака:
При сложении чисел в ОК и ДК были получены переносы в знаковый разряд и из знакового разряда.
В случае ОК перенос из знакового разряда требует дополнительного прибавления единицы младшего разряда.
В случае ДК этот перенос игнорируется.
Пример сложения чисел +18 и –7 приведен в таблице.
Прямой, дополнительный и обратный коды
Прямой, дополнительный и обратный код числа (создан по запросу).
Далее идет калькулятор, который переводит введенное положительное или отрицательное целое число в двоичный код, а также выводит обратный код этого числа и его дополнительный код. Под калькулятором, как водится, немного теории.
Обновление: Из комментариев становится ясно, что люди не вполне понимают, что делает этот калькулятор. Точнее, что делал — применял алгоритм вычисления дополнительного кода к любому числу. Люди хотят, чтобы он им просто показывал дополнительный код числа. Ну хорошо — теперь при вводе положительного числа калькулятор показывает представление числа в двоичной форме, ибо для него нет обратного и дополнительного кода, а при вводе отрицательного показывает дополнительный и обратный код.
Прямой, дополнительный и обратный код
Прямой код числа это представление беззнакового двоичного числа. Если речь идет о машинной арифметике, то как правило на представление числа отводится определенное ограниченное число разрядов. Диапазон чисел, который можно представить числом разрядов n равен
Обратный код числа, или дополнение до единицы (one’s complement) это инвертирование прямого кода (поэтому его еще называют инверсный код). То есть все нули заменяются на единицы, а единицы на нули.
Дополнительный код числа, или дополнение до двойки (two’s complement) это обратный код, к младшему значащему разряду которого прибавлена единица
А теперь «зачем, зачем это все?» ©
Для различия положительных и отрицательных чисел выделяют старший разряд числа, который называется знаковым (sign bit)
0 в этом разряде говорит нам о том, что это положительное число, а 1 — отрицательное.
С положительными числами все вроде бы понятно, для их представления можно использовать прямой код
0 — 0000
1 — 0001
7 — 0111
А как представить отрицательные числа?
И это оказалось очень удобно для машинных вычислений — при таком представлении отрицательного числа операции сложения и вычитания можно реализовать одной схемой сложения, при этом очень легко определять переполнение результата (когда для представления получившегося числа не хватает разрядности)
Пара примеров
7-3=4
0111 прямой код 7
1101 дополнительный код 3
0100 результат сложения 4
-1+7=6
1111 дополнительный код 1
0111 прямой код 7
0110 результат сложения 6
Что касается переполнения — оно определяется по двум последним переносам, включая перенос за старший разряд. При этом если переносы 11 или 00, то переполнения не было, а если 01 или 10, то было. При этом, если переполнения не было, то выход за разряды можно игнорировать.
Примеры где показаны переносы и пятый разряд
00111 прямой код 7
00001 прямой код 1
01110 переносы
01000 результат 8 — переполнение
Два последних переноса 01 — переполнение
-7+7=0
00111 прямой код 7
01001 дополнительный код 7
11110 переносы
10000 результат 16 — но пятый разряд можно игнорировать, реальный результат 0
Два последних переноса 11 з перенос в пятый разряд можно отбросить, оставшийся результат, ноль, арифметически корректен.
Опять же проверять на переполнение можно простейшей операцией XOR двух бит переносов.
Вот благодаря таким удобным свойствам дополнительный код это самый распространенный способ представления отрицательных чисел в машинной арифметике.
Прямой, обратный и дополнительный коды двоичного числа
Прямой код двоичного числа
Обратный код двоичного числа
Дополнительный код двоичного числа

Мы знаем, что десятичное число можно представить в двоичном виде. К примеру, десятичное число 100 в двоичном виде будет равно 1100100, или в восьмибитном представлении 0110 0100. А как представить отрицательное десятичное число в двоичном виде и произвести с ним арифметические операции? Для этого и предназначены разные способы представления чисел в двоичном коде.
Сразу отмечу, что положительные числа в двоичном коде вне зависимости от способа представления (прямой, обратный или дополнительный коды) имеют одинаковый вид.
Прямой код
Обратный код
Для неотрицательных чисел обратный код двоичного числа имеет тот же вид, что и запись неотрицательного числа в прямом коде.
Для отрицательных чисел обратный код получается из неотрицательного числа в прямом коде, путем инвертирования всех битов (1 меняем на 0, а 0 меняем на 1).
Для преобразования отрицательного числа записанное в обратном коде в положительное достаточного его проинвертировать.
Арифметические операции с отрицательными числами в обратном коде:
Дополнительный код
В дополнительном коде (как и в прямом и обратном) старший разряд отводится для представления знака числа (знаковый бит).
Арифметические операции с отрицательными числами в дополнительном коде
Вывод:
1. Для арифметических операций сложения и вычитания положительных двоичных чисел наиболее подходит применение прямого кода
2. Для арифметических операций сложения и вычитания отрицательных двоичных чисел наиболее подходит применение дополнительного кода


Записать в прямом обратном и дополнительном кодах
2. Основы машинной арифметики с двоичными числами.
Любая информация (числа, команды, записи и т. п.) представляется в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. Двоичный код состоящий из 8 разрядов носит название байта. Для записи чисел также используют 32-разрядный формат (машинное слово), 16-разрядный формат (полуслово) и 64-разрядный формат (двойное слово).
В ЭВМ в целях упрощения выполнения арифметических операций применяют специальные коды для представления чисел. Использование кодов позволяет свести операцию вычитания чисел к арифметическому сложению кодов этих чисел. Применяются прямой, обратный и дополнительный коды чисел. Прямой код используется для представления отрицательных чисел в запоминающем устройстве ЭВМ, а также при умножении и делении. Обратный и дополнительный коды используются для замены операции вычитания операцией сложения, что упрощает устройство арифметического блока ЭВМ. К кодам выдвигаются следующие требования:
1) Разряды числа в коде жестко связаны с определенной разрядной сеткой.
2) Для записи кода знака в разрядной сетке отводится фиксированный, строго определенный разряд.
Например, если за основу представления кода взят один байт, то для представления числа будет отведено 7 разрядов, а для записи кода знака один разряд.
Прямой код. Прямой код двоичного числа совпадает по изображению с записью самого числа. Значение знакового разряда для положительных чисел равно 0, а для отрицательных чисел 1.
Знаковым разрядом обычно является крайний разряд в разрядной сетке. В дальнейшем при записи кода знаковый разряд от цифровых условимся отделять запятой. Если количество разрядов кода не указано будем предполагать, что под запись кода выделен один байт.
Обратный код. Обратный код для положительного числа совпадает с прямым кодом. Для отрицательного числа все цифры числа заменяются на противоположные (1 на 0, 0 на 1), а в знаковый разряд заносится единица.
Дополнительный код. Дополнительный код положительного числа совпадает с прямым кодом. Для отрицательного числа дополнительный код образуется путем получения обратного кода и добавлением к младшему разряду единицы.
Для числа +1101:
| Прямой код | Обратный код | Дополнительный код |
| 0,0001101 | 0,0001101 | 0,0001101 |
2.2 Особенности сложения чисел в обратном и дополнительном кодах.
При сложении чисел в дополнительном коде возникающая единица переноса в знаковом разряде отбрасывается.
При сложении чисел в обратном коде возникающая единица переноса в знаковом разряде прибавляется к младшему разряду суммы кодов.
Если результат арифметических действий является кодом отрицательного числа, необходимо преобразовать его в прямой код. При этом обратный код преобразуется в прямой заменой цифр во всех разрядах кроме знакового на противоположные. Дополнительный код преобразуется в прямой также, как и обратный, с последующим прибавлением единицы к младшему разряду.
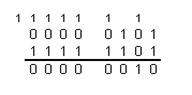
Сложить двоичные числа X и Y в обратном и дополнительном кодах.
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
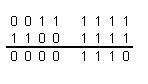
1) Сложим числа, пользуясь правилами двоичной арифметики:
2) Сложим числа, используя коды:
| Прямой код | Сложение в обратном коде | Сложение в дополнительном коде |
2.3 Модифицированные обратный и дополнительный коды.
При переполнении разрядной сетки, происходит перенос единицы в знаковый разряд. Это приводит к неправильному результату, причем положительное число, получившееся в результате арифметической операции может восприниматься как отрицательное (так как в знаковом разряде «1») и наоборот.
Рассмотрим предыдущий пример, выполнив сложение в модифицированном обратном коде:
1) Переведем X и Y в модифицированный дополнительный код:











 2 0
2 0 7 6 5 4 3 2 1 0
7 6 5 4 3 2 1 0