самая лучшая фигура в геометрии
Основные геометрические фигуры
Основные понятия
Основные геометрические фигуры на плоскости — это точка и прямая линия. А простейшие фигуры — это луч, отрезок и ломаная линия.
Минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет размеров: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах измерения длины, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения площади:
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Примеры объемных геометрических фигур:
Рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Узнать площадь прямоугольника помогут следующие формулы:
Диагональ — это отрезок, который соединяет противоположные вершины фигуры. Он есть во всех фигурах, число вершин которых больше трех.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Найти площадь квадрата легко:
Периметр квадрата — это длина стороны, умноженная на четыре.
P = 4 × a, где a — длина стороны.
Трапеция
Трапеция — это четырехугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее оснований равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 × h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и был расположен перпендикулярно к этим основаниям.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у равнобедренной трапеции есть две равные стороны.
P = a + b + 2 × c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны
Ромб — это параллелограмм с равными сторонами.
Общие формулы расчета площади фигур:
Периметр ромба — это произведение длины стороны на четыре.
P = 4 × a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 × (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это такая фигура, которая образуется, когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
S = 0,5 × a × h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
S = 0,5 × a × b × sinα, где a и b — две стороны, sinα — синус угла между ними.
S = (a × b × с) : 4 × R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
S = p × r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это длины стороны, умноженная на три.
P = 3 × a, где a — длина стороны.
Круг — это множество точек на плоскости, которые удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
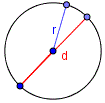
Радиус окружности — это расстояние от центра окружности до любой точки на ней.
Диаметр круга — это отрезок, который соединяет две точки на окружности и проходящий через ее центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d × π = 2 × r × π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Никогда не задумывались, почему треугольник самая крутая фигура?
Самая простая фигура это точка. Точка не имеет ни длины ни ширины. Точка вообще ничего не имеет.
Если взять две прямые и соединить их точкой, Получим угол. Про угол известно, что он может быть острым, прямым или тупым. Да да, тупой угол ха-ха. А еще у угла есть подружка которую зовут биссектриса. Про нее известно, что она бегает по углам и делит угол пополам.
Примечание1. Кот найдет в интернетах, как свидетельство крутизны треугольника.
Примечание2. Я не знаю зачем я это написал
Автор, пофиг на завидующих. Я с тобой согласен полностью. Мало того самые крутые котики ложатся в треугольник. В плане морды. Его можно брать как эталон крутости чего угодно. Помимо того что это самая сакральная и часто встречающаяся форма мире. Все что угодно можно свести в треугольник. а его самого только тоже в треугольник. Самый мощный перкуссионный инструмент в оркестре? Треугольник. А если взять два треугольника. то сами знаете что.
«Прямая имеет длину, если она отрезок. Или направление, если она луч.»
Все уроки математики даром
— А ты почему не работаешь!?
Ипотека
Покупатель не Спартак, не вымрет
Год назад
OZON, вы какие то чудные.
Решил заказать 6 пачек стирального порошка по 3 кг (скидка под 50%).
Заказываю с выдачей в постомате. Сумма порядка 1900 рублей.
Отказ. «Слишком габаритная посылка».
Ладно. Разбиваю на 2 заказа по 3 пачки порошка в каждом.
Опять не так. Недостачная стоимость заказа (Чуть меньше тысячи в каждом). Ладно. Добавляю по одноразовой бритве в каждый заказ. Всё норм, оплачиваю.
Приходит заказ в постомат. 8 посылок. 8 ячеек. 8 кодов. Одну бритву забираю из ячейки размера такого, что 10 летнего ребёнка можно поместить. Остальные ячейки поменьше, но каждый пакет порошка в своей ячейке и занимает от силы 10% её объёма. Забирал заказ наверное минут 15.
Герои среди нас
Домой, в Белгород, милиционер вернулся только через год. И как обещал до командировки, первым делом женился.
Ответ на пост «Куплю квартиру в Вашем доме. »
Маг воды
Дефицит русских? Нет
Я слышал, что Яндекс планирует запретить мигрантам работать в такси, либо такие правила уже введены, да только пока ничего не изменилось. Яндекс, может как-то ситуацию уже начнете менять?
8 необычных геометрических форм, о существовании которых ты вряд ли знал
Какие фигуры ты знаешь? Квадрат, круг, треугольник. Этого вполне достаточно для повседневных задач. Но форм куда больше, чем ты можешь себе представить, и они порой настолько необычные, что кажется, будто их выдумали, просто чтобы потренироваться в фантазии.
1. Тор
Если говорить научным языком, тор, или, как его ещё называют, тороид, — это поверхность, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её. Звучит непонятно, и человеку, незнакомому с геометрией, вообще невозможно представить, что это такое.
А на самом деле всё просто, ведь тор ты видишь каждый день — это форма бублика, пончика, спасательного круга, шины колеса и всего похожего на них. Что касается природы, то и в ней встречаются такие фигуры. Например, форму тора имеют вихревые потоки, электромагнитные поля, траектории элементарных частиц.
Так что в следующий раз, когда тебя спросят, какую форму имеет пончик, можешь сказать, что это тор.
2. Треугольник Рёло
Треугольник Рёло — это область пересечения трёх равных кругов с центрами в вершинах правильного треугольника и радиусами, равными его стороне. Сам треугольник чем-то напоминает медиатор для гитары и имеет не прямые, а изогнутые грани.
Его ты тоже регулярно встречаешь в обычной жизни. Так, например, треугольник Рёло используют в сфере искусства для уже упомянутых струнных инструментов, а также при рисовании различных диаграмм, где несколько элементов по кругу, сочетаясь между собой, приводят к центральному ядру.
Кроме того, треугольник Рёло — это одна из первых изобретённых человеком форм, так как древние люди, изготавливая свои примитивные орудия труда из камня, нередко обтачивали их именно в такой форме, что позволяло использовать их с любой стороны.
3. Гиперболоид
Гиперболоид — это трёхмерная форма, которая напоминает песочные часы. Существуют однополостные и двухполостные гиперболоиды. Вторые ты можешь увидеть в тех знаменитых тарелках спутниковой связи, а также в телескопах, если интересуешься астрономией. Не путай гиперболоид с гиперболой — это разные вещи.
4. Аполлонийская прокладка, или аполлоническая сетка
Это очень сложная фигура, состоящая из одного большого круга с кругами меньшего размера, которые заполняют пространство внутри него.
Эта фигура редко где используется, и её можно было встретить в старых калейдоскопах, а также в искусстве. В художественных школах иногда ученики рисуют аполлонийские прокладки для отработки навыка рисования ровных кругов от руки.
5. Балбис
Думаешь, что буква Н — это просто буква? На самом деле это геометрическая форма, которую по-простому можно описать как одну первичную линию, которая завершается вторичной линией на одном конце и ещё одной — на другом. Завершающие линии располагаются под прямым углом к первичной, а его параллельные стороны могут быть бесконечно длинными.
6. Лента Мёбиуса
Про эту фигуру ты мог слышать в каких-нибудь фантастических фильмах, да и то редко. Это простейшая неориентируемая поверхность, являющаяся односторонней и непрерывной в трёхмерном пространстве. Лучше увидеть ленту Мёбиуса своими глазами, чтобы понять, что это такое. Если ты хочешь пошутить над человеком, то просто попроси его развернуть ленту Мёбиуса так, чтобы она не изгибалась. Заранее скажем, что сделать это невозможно.
7. «Рыбий пузырь»
Эта фигура больше известна как Vesica piscis, и она образована пересечением двух кругов с одинаковым радиусом, наложенных так, что центр одного лежит на окружности другого.
Где ты мог видеть такую фигуру? К примеру, в эмблеме Audi или Олимпийских игр. Также «рыбий пузырь» можно встретить в средневековой архитектуре в орнаментах и мозаиках.
8. Лемниската
Не зря лемниската идет у нас под восьмым номером, ведь своим видом она напоминает именно эту цифру, а также символ бесконечности. Эта плоская алгебраическая кривая может иметь несколько фиксированных фокусов, и от количества точек будет зависеть её конечная форма.
Удивительные фигуры в геометрии
Геометрия – точная математическая наука, которая занимается изучением пространственных и других подобных отношений и форм. Но ее часто называют «сухой», поскольку она не способна описать форму многих природных объектов, ведь облака – это не сферы, горы – не конусы, а молнии распространяются не по прямым линиям. Многие объекты в природе отличаются сложностью форм в сравнении со стандартной геометрией.
Тем не менее, существует ряд удивительных фигур, которые обычно не изучаются на школьных уроках геометрии, но именно они окружают человека в реальном мире: в природе и архитектуре, головоломках, компьютерных играх и т. д.
Фрактал
Главное свойство этой сложной геометрической фигуры – самоподобие, то есть она состоит из нескольких частей, каждая из которых подобна целому объекту. Именно это свойство отличает фракталы от объектов классической (или, как говорят, евклидовой) геометрии.
При этом сам термин «фрактал» не является математическим и не имеет однозначного определения, поэтому может применяться к объектам, которые являются самоподобными или приближенно самоподобными. Его придумал в 1975 г. Бенуа Мандельброт, позаимствовав латинское слово «fractus» (ломанный, дробленный).
Фрактальные формы как нельзя лучше подходят для описания реального мира и часто встречаются среди природных объектов: снежинок, листьев растений, системы кровеносных сосудов человека и животных.
Лента Мебиуса
Это одна из самых необыкновенных трехмерных фигур в геометрии, которую легко сделать в домашних условиях. Для этого достаточно взять бумажную полоску, ширина которой в 5-6 раз меньше ее длины, и, перекрутив один из концов на 180°, склеить их между собой.
Если все сделано правильно, то можно проверить самостоятельно ее удивительные свойства:
Лента Мебиуса широко используется в промышленности и науке (в ленточных конвейерах, матричных принтерах, механизмах для заточки и пр.). Кроме этого существует научная гипотеза, по которой сама Вселенная также представляет собой ленту Мебиуса невероятных размеров.
Полимино
Это плоские геометрические фигуры, которые образуются за счет соединения нескольких квадратов равных размеров по их сторонам.
Названия полимино зависят от количества квадратов, из которых они сформированы:
При этом для каждой разновидности существует разное количество типов фигур: у домино 1 тип, у тримино – 3 типа, у гексамино (из 6 квадратов) – 35 типов. Число различный вариаций зависит от количества используемых квадратов, но при этом еще никому из ученых не удалось найти удивительную формулу, которая будет выражать эту зависимость. Из деталей полимино можно выкладывать как геометрические фигуры, так и изображения людей, животных, предметов. Несмотря на то, что это будут схематичные силуэты, основные признаки и формы предметов делают их вполне узнаваемыми.
Полиамонд
Наряду с полимино, существует еще одна удивительная геометрическая фигура, используемая для составления других фигур – полиамонд. Он представляет собой многоугольник, сформированный из нескольких равносторонних треугольников равного размера.
Название придумал математик Т. О’Бейрн на основании одного из названий ромба в английском языке – диамонд, который можно составить из 2-х равносторонних треугольников. По аналогии, фигуру из 3-х равносторонних треугольников О’Бейрн назвал триамондом, из 4-х – тетриамондом и т. д.
Главным вопросом их существования остается вопрос о возможном количестве полиамондов, которые можно составить из определенного количества треугольников. Применение полиамондов в реальной жизни также аналогично использованию полимино. Это могут быть разного рода головоломки и логические задачи.
Треугольник Рело
Как ни удивительно звучит, но с помощью дрели можно просверлить квадратное отверстие, а помогает в этом треугольник Рело. Он представляет собой область, образованную посредством пересечения 3 равных окружностей, центры которых являются вершинами правильного треугольника, а радиусы равны его стороне.
Сам треугольник Рело назван по фамилии немецкого ученого-инженера, который первым наиболее детально исследовал его особенности и использовал для своих механизмов на рубеже XIX-XX в. в., хотя его удивительные свойства были известны еще Леонардо да Винчи. Кто бы ни был его первооткрывателем, в современном мире эта фигура нашла широкое применение в виде:
Невозможные фигуры
Отдельного внимания заслуживают так называемые невозможные фигуры – удивительные оптические иллюзии, которые на первый взгляд кажутся проекцией трехмерного объекта, но при ближайшем рассмотрении становятся заметны необычные соединения элементов. Наиболее популярными из их числа являются:
Трибар, созданный отцом и сыном Лайонелом и Роджером Пенроузами, который представляет собой изображение равностороннего треугольника, но имеет странные закономерности. Стороны, образующие верхнюю часть треугольника кажутся перпендикулярными, но правая и левая грани в нижней части также кажутся перпендикулярными. Если рассматривать каждую часть этого треугольника по отдельности, еще можно признать их существование, но в действительности такая фигура существовать не может, поскольку при ее создании были неправильно соединены правильные элементы.
Бесконечная лестница, авторство которой также принадлежит отцу и сыну Пенроузам, поэтому ее часто называют по их имени – «лестницей Пенроуза», а также «Вечной лестницей». На первый взгляд, она выглядит как обычная, ведущая вверх или вниз лестница, но при этом человек, шагающий по ней будет непрерывно подниматься (против часовой стрелки) или опускаться (по часовой стрелке). Если визуально путешествовать по такой лестнице, то по окончании «путешествия» взгляд останавливается в точке начала пути. Если бы такая лестница существовала в действительности, по ней пришлось бы подниматься и спускаться бесконечное число раз, что можно сравнить с бесконечным сизифовым трудом.
Невозможный трезубец – удивительный объект, глядя на который невозможно определить, где начинается средний зубец. Он также основан на принципе неправильных соединений, которые могут существовать только в двухмерном, но не трехмерном пространстве. Рассматривая части трезубца по отдельности, с одной стороны видны 3 круглых зуба, с другой стороны – 2 прямоугольных.
Таким образом, части фигуры вступают в своеобразный конфликт: во-первых, происходит смена переднего и заднего плана, во-вторых круглые зубцы в нижней части трансформируются в плоские в верхней.
Геометрические фигуры — виды с названиями и основные свойства
Скопление точек и линий на плоскости образует геометрические фигуры. Их названия зависят от свойств и особенностей. Фигура ограничена линиями и это условие влияет на многообразие форм. Каждый предмет индивидуален, имеет свои предназначения и задачи. Существуют простые и сложные фигуры, различающиеся личными параметрами.
Общая характеристика
Предметы в геометрическом изображении состоят из отдельных частей: точек, линий, лучей, отрезков и вершин. Отдельно взятый предмет имеет свое предназначение.
Основные понятия о составляющих
Когда все точки фигуры принадлежат одной плоскости, она является плоской. К ней относятся отрезок, прямоугольник. Существуют геометрические объекты, не являющиеся разновидностью плоскости, — куб, шар, пирамида, призма.
Минимальным объектом геометрии является точка. Определение того, какой она должна быть известно из школьного математического курса. Учебник характеризует ее как объект, не имеющий измерительных особенностей. Точка (Т) не содержит стандартных свойств: высоты, длины, радиуса, важным является только ее расположение. Обозначается числом или большой заглавной буквой. Например, точка называется D, E, F или 1, 2, 3. Несколько точек бывают отмечены разными цветами или буквами для удобного различия.
Линия состоит из множества точек. Измеряется длина этого составляющего объекта и обозначается маленькими буквами (abc).
Виды линий:
Задания из школьной программы кажутся школьникам скучными, неинтересным, но эти азы являются основой составления фигур простых и более сложных.
Существуют подвиды прямой линии: пересекающиеся, содержащие общую точку и когда две прямые линии соединяются в одной точке.
Луч в математике представляет часть прямой, имеющей начальную точку, но не имеющую конец. Это продолжение в одну сторону. Если Т разделяет линию пополам — получается два луча. Лучевые линии совпадают, когда расположены на одной прямой, начинаются в точке или направляются в одну сторону.
Отрезок представляет составную часть прямой, ограниченной двумя точками — она имеет начало и конец, поэтому измеряется. Длина отрезка представляет расстояние между его первой и последней точками. Через одну Т проводится бесконечное число линий, а через две — кривые и только одна прямая.
Стандартные объекты
К основным фигурам геометрии на плоскости относятся прямоугольник, треугольник, квадрат, многоугольник и круг. Прямоугольник выглядит как фигура, состоящая из четырех сторон и четырех прямых углов (ПУ). Противоположные стороны равны между собой. В математике прямоугольник обозначается четырьмя латинским заглавными буквами. Все ПУ расположены под 90 градусов. Прямоугольник с равными, одинаковыми сторонами называется квадратом.
Фигура, имеющая 3 стороны и столько же углов (вершин), называется треугольником. Существует классификация этой фигуры по типу У.
Виды треугольника в зависимости от угла (У):
Геометрическая фигура с углами разной формы называется многоугольником. Его вершины представлены точками, соединяющими отрезками.
Радиус круга — промежуток от середины окружности до любой ее точки. Диаметр — это отрезок, соединяющий две точки окружности, проходящий через ее середину.
Параллелепипед — это призма, у которой основанием является параллелограмм. Когда все ребра параллелепипеда равны, получается куб.
Многогранная фигура, у которой одна грань является многоугольником, а остальные грани (боковые) — треугольники с общей вершиной, называется пирамидой.
Семиугольник (гептагон) — это многоугольник с 7 углами. Многоугольник представляет замкнутую ломанную линию.
Основные фигуры перечислены, но геометрия включает еще сложные объекты, использующиеся в различных областях жизни.
Сложные модели
В сложной геометрии выделяют фигуры с пространственным, плоским и объемным наполнением. Существует понятие геометрического тела, 3D-моделирование и проекция.
Определение тела и пространства
Геометрическое тело (ГТ) представляет часть пространства, отделенное замкнутой поверхностью наружной границы. Это понятие относится к компактному множеству точек, а две из них соединяют отрезком, проходящим внутри границы тела. Внешняя граница ГТ является его гранью, которых может быть несколько. Множество плоских граней определяет вершины и ребра ГТ. Все геометрические тела делятся на многогранники и тела вращения.
Тела вращения — объемные тела, образующиеся из-за вращения плоской фигуры, ограниченной кривой, вокруг оси. Эта ось расположена в той же плоскости. При вращении контуров фигур вокруг собственной оси возникает поверхность вращения, а если вращать заполненные контуры — возникают объекты (шар).
Шар представляет множество точек, расположенных от данной точки на небольшом пространстве. Точка является центром шара, а расстояние ограничено радиусом.
В сферу геометрии входят плоские (двухмерные) и объемные пространственные фигуры (трехмерные).
Плоские фигуры представляют точка, круг, полукруг, окружность, овал, прямоугольник, квадрат, луч, ромб, трапеция.
Существуют двухмерные фигуры (2D), представленные углом, многоугольником, четырехугольником, окружностью, кругом, эллипсом и овалом. Объекты 3D выделены двугранным или многогранным углом. Среди них известны призма, параллелепипед, куб, антипризма, пирамида, тетраэдр икосаэдр, бипирамида, геоид, эллипсоид, сфера шар и другие. Плоские фигуры изучает планиметрия, а объемные — стереометрия.
Объемные фигуры:
Конус образуется из треугольника с прямыми углами, при вращении его вокруг одного из катетов. Тороид возникает из замкнутой плоскости (окружности), вращающейся вокруг прямой и не пересекающей ее. Многогранник называется полиэдр, представляет замкнутую поверхность, состоящую из многоугольников.
Виды многогранников:
В школьной программе имеются специальные разделы геометрии, позволяющие распределить знания и не путать их в будущем. Это касается плоских, объемных фигур — одни изучает стереометрия, другие планиметрия.
Познавательные игрушки детям
Геометрия является наукой, которой можно знакомить детей с раннего возраста. Лучше распечатать картинки, геометрические фигуры для детей, затем нарисовать их вместе на чистом листе. Малышу первого года подобное занятие будет не очень интересным и понятным, а у дошкольника вызовет интерес, особенно если объекты изучения будут разноцветными или в необычном исполнении.
Основной материал для обучения детей:
Увлекательные, забавные, задорные стихи «Веселая геометрия для малышей» помогут детям быстро познакомиться и усвоить много важной информации о фигурах и размерах предметов. Веселые стишки помогут юному читателю соотнести малопонятные геометрические знания с обыденными предметами обихода. Например, в женской юбке представлена трапеция, в блюдце— круг, а в трубе цилиндр.
Учить детей начинают с плоских фигурок, сделанных из цветной бумаги или фетра. Не нужно ограничивать ребенка в фантазии, ведь он различает фигуры по цветам и форме — треугольник, овал, круг, ромб, квадрат. Увлекательным будет занятие с использованием сортеров, пирамидок из различных геометрических объектов.
Ближе к дошкольному возрасту переходят на объемные фигуры, кубики, конусы, кольца и цилиндры. В школьном возрасте знания накопятся, и дети будут осознанно различать равнобедренный, равносторонний треугольник, три понятия: луч, отрезок, окружность.
Раздел математики геометрия изучает пространственные отношения и формы. Фигура как понятие, рассмотренное во всех учебниках геометрии, является пространственной формой.
Геометрию можно обнаружить везде — в любых окружающих предметах. Это современные здания, архитектурные строения, формы, космическая станция, интерьер квартиры, подводные лодки.
Математические знания являются профессионально важными для современных специальностей: дизайнеров и конструкторов, рабочих и ученых. Без знания основ геометрии невозможно построить здание или отремонтировать квартиру.