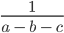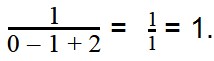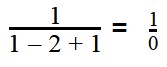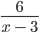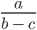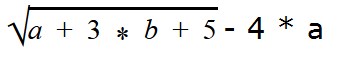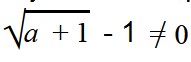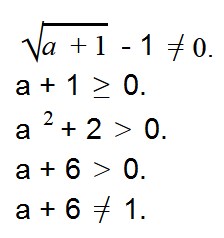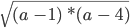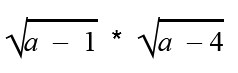квадратом какого выражения является выражение 16x4y6
Область допустимых значений функции
Допустимые и недопустимые значения переменных
В 7 классе заканчивается математика и начинается ее-величество-алгебра. Первым делом школьники изучают выражения с переменными.
Мы уже знаем, что математика состоит из выражений — буквенных и числовых. Каждому выражению, в котором есть переменная, соответствует область допустимых значений (ОДЗ). Если игнорировать ОДЗ, то в результате решения можно получить неверный ответ. Получается, чтобы быстро получить верный ответ, нужно всегда учитывать область допустимых значений.
Чтобы дать верное определение области допустимых значений, разберемся, что такое допустимые и недопустимые значения переменной.
Рассмотрим все необходимые определения, связанные с допустимыми и недопустимыми значениями переменной.
Выражение с переменными — это буквенное выражение, в котором буквы обозначают величины, принимающие различные значения.
Значение числового выражения — это число, которое получается после выполнения всех действий в числовом выражении.
Выражение с переменными имеет смысл при данных значениях переменных, если при этих значениях переменных можно вычислить его значение.
Выражение с переменными не имеет смысла при данных значениях переменных, если при этих значениях переменных нельзя вычислить его значение.
Теперь, опираясь на данные определения, мы можем сформулировать, что такое допустимые и недопустимые значения переменной.
Допустимые значения переменных — это значения переменных, при которых выражение имеет смысл.
Если при переменных выражение не имеет смысла, то значения таких переменных называют недопустимыми.
В выражении может быть больше одной переменной, поэтому допустимых и недопустимых значений может быть больше одного.
Пример 1
Рассмотрим выражение
В выражении три переменные (a, b, c).
Запишем значения переменных в виде: a = 1, b = 1, c = 2.
Такие значения переменных являются допустимыми, поскольку при подстановке этих значений в выражение, мы легко можем найти ответ:
Таким же образом можем выяснить, какие значения переменных — недопустимые.
Подставим значения переменных в выражение
На ноль делить нельзя.
Что такое ОДЗ
ОДЗ — это невидимый инструмент при решении любого выражении с переменной. Чаще всего, ОДЗ не отображают графически, но всегда «держат в уме».
Область допустимых значений (ОДЗ) — это множество всех допустимых значений переменных для данного выражения.
Пример 2
Рассмотрим выражение
Пример 3
Рассмотрим выражение
ОДЗ такого выражения будет выглядеть вот так: b ≠ c; a — любое число.
Такая запись означает, что область допустимых значений переменных b, c и a = это все значения переменных, при которых соблюдаются условия b ≠ c; a — любое число.
Как найти ОДЗ: примеры решения
Найти ОДЗ — это значит, что нужно указать все допустимые значения переменных для выражения. Часто, чтобы найти ОДЗ, нужно выполнить преобразование выражения.
Чтобы быстро и верно определять ОДЗ, запомните условия, при которых значение выражения не может быть найдено.
Мы не можем вычислить значение выражения, если:
Теперь, приступая к поиску ОДЗ, вы можете сверять выражение по всем этим пунктам.
Давайте потренируемся находить ОДЗ.
Пример 4
Найдем область допустимых значений переменной выражения a 3 + 4 * a * b − 6.
В куб возводится любое число. Ограничений при вычитании и сложении нет. Это значит, что мы можем вычислить значение выражения a 3 + 4 * a * b − 6 при любых значениях переменной.
ОДЗ переменных a и b — это множество таких пар допустимых значений (a, b), где a — любое число и b — любое число.
Ответ: (a и b), где a — любое число и b — любое число.
Пример 5
Найдем область допустимых значений (ОДЗ) переменной выражения
Здесь нужно обратить внимание на наличие нуля в знаменатели дроби. Одним из условий, при котором вычисление значения выражения невозможно явлется наличие деления на ноль.
Это значит, что мы может сказать, что ОДЗ переменной a в выражении 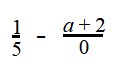
Пустое множество изображается в виде вот такого символа Ø.
Пример 6
Найдем область допустимых значений (ОДЗ) переменных в выражении
Если есть квадратный корень, то нам нужно следить за тем, чтобы под знаком корня не было отрицательного числа. Это значит, что при подстановке значений a и b должны быть условия, при которых a + 3 * b + 5 ≥ 0.
Ответ: ОДЗ переменных a и b — это множество всех пар, при которых a + 3 * b + 5 ≥ 0.
Пример 7
Найдем ОДЗ переменной a в выражении
Прежде всего, нам нужно подобрать такое условие, при котором в знаменателе дроби не будет ноля —
Мы знаем, что выражение под знаком корня должно быть положительным. Это дает нам второе условие: a + 1 ≥ 0.
Мы не можем вычислить логарифм отрицательного выражения. Получаем третье условие: a 2 + 2 > 0.
Выражении в основании логарифма не должно быть отрицательным и не должно равняться единице. Получаем условие 4: a + 6 > 0.
Как видите, записывая ОДЗ, мы ставим квадратные и круглые скобки.
Запомните
Например, если х > 6, но х
Зачем учитывать ОДЗ при преобразовании выражения
Иногда выражение просто невозможно решить, если не выполнить ряд тождественных преобразований. К ним относятся: перестановки, раскрытие скобок, группировка, вынесение общего множителя за скобки, приведение подобных слагаемых.
Кроме того, что видов таких преобразований довольно много: нужно понимать, в каких случаях какое преобразование возможно. В этом может помочь определение ОДЗ.
Тождественное преобразование может:
Рассмотрим каждый случай в отдельности.
Пример 8
Поскольку мы должны следить за тем, чтобы в выражении не возникало деление ноль, определяем условие a ≠ 0.
Это условие отвечает множеству (−∞ ; 0) ∪ (0 ; +∞).
В выражении есть подобные слагаемые, если привести подобные слагаемые, то мы получаем выражение вида a.
ОДЗ для a — это R — множество всех вещественных чисел.
Преобразование расширило ОДЗ — добавился ноль.
Пример 9
Рассмотрим выражение a 2 + a + 4 * a
ОДЗ a для этого выражения — множество R.
В выражении есть подобные слагаемые, выполним тождественное преобразование.
После приведения подобных слагаемых выражение приняло вид a 2 + 5 * a
ОДЗ переменной a для этого выражения — множество R.
Это значит, что тождественное преобразование никак не повлияло на ОДЗ.
Пример 10
Рассмотрим выражение
Решить такое неравенство можно методом интервалов, что дает нам ОДЗ (−∞; 1] ∪ [4 ; +∞).
Затем выполним преобразование исходного выражения по свойству корней: корень произведения = произведению корней.
Приведем выражение к виду
Решив систему линейных неравенств, получаем множество [4; + ∞).
Отсюда видно, что тождественные преобразования сузили ОДЗ.
От (−∞; 1] ∪ [4 ; +∞) до [4; + ∞).
Решив преобразовать выражение, внимательно следите за тем, чтобы не допустить сужение ОДЗ.
Запомните, что выполняя преобразование, следует выбирать такие, которые не изменят ОДЗ.
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Записаться на марафон
Бесплатный марафон: как самому создавать игры, а не только играть в них (◕ᴗ◕)
Какое выражение является квадратом одночлена 6m ^ 4n ^ 5A)12m ^ 8n ^ 10 ; B)12m ^ 16n ^ 26 ; C)36m ^ 16n ^ 25Решение обязательно?
Какое выражение является квадратом одночлена 6m ^ 4n ^ 5
A)12m ^ 8n ^ 10 ; B)12m ^ 16n ^ 26 ; C)36m ^ 16n ^ 25
Ответ C) 36 m ^ 16 n ^ 25 = (6m ^ n ^ 12, 5)².
Представте выражение в виде квадрата одночлена 16a⁴b²?
Представте выражение в виде квадрата одночлена 16a⁴b².
Запишите одночлен в виде квадрата другого одночлена а)49а⁴b¹²?
Запишите одночлен в виде квадрата другого одночлена а)49а⁴b¹².
Како из чисел является решением неравентсва х в квадрате>9?
Како из чисел является решением неравентсва х в квадрате>9.
Представьте данное выражение в виде куба или квадрата другого одночлена : а) б)?
Представьте данное выражение в виде куба или квадрата другого одночлена : а) б).
Записать одночлен в виде квадрата другого одночлена 9a в квадрате?
Записать одночлен в виде квадрата другого одночлена 9a в квадрате.
Запишите данный одночлен в виде квадрата некоторого одночлена?
Запишите данный одночлен в виде квадрата некоторого одночлена.
Представьте выражение в виде квадрата одночлена m4n8 ; 1 / 4m6n2 ; 0, 0025x4y12?
Представьте выражение в виде квадрата одночлена m4n8 ; 1 / 4m6n2 ; 0, 0025x4y12.
Представьте выражение в виде квадрата одночлена a4 b6 a2b8 x2y10?
Представьте выражение в виде квадрата одночлена a4 b6 a2b8 x2y10.
Можно ли представить одночлен C в виде квадрата некоторого одночлена D, если C = 25a10?
Можно ли представить одночлен C в виде квадрата некоторого одночлена D, если C = 25a10?
(Если представить одночлен в виде квадрата некоторого одночлена нельзя, в первом и втором окошке напиши «нет»).
Представив выражение 0, 64m12n10k18 в виде квадрата одночлена, получим :
Квадратом какого выражения является одночлен 81a ^ 4b ^ 6?
Квадратом какого выражения является одночлен 81a ^ 4b ^ 6?
1300÷500 = 2, 6 пачки в неделю 2, 6×7 = 18, 2 пачки на 7 недель ответ : 19 пачек.
Информатика ЕГЭ 15 задание разбор
15 задание ЕГЭ «Основные законы алгебры логики»
15-е задание: «Основные законы алгебры логики»
Уровень сложности — повышенный,
Требуется использование специализированного программного обеспечения — нет,
Максимальный балл — 1,
Примерное время выполнения — 5 минут.
Проверяемые элементы содержания: Знание основных понятий и законов математической логики
Плейлист видеоразборов задания на YouTube:
Задания с множествами
Элементами множества А являются натуральные числа. Известно, что выражение
Ответ: 12
Элементами множества А являются натуральные числа. Известно, что выражение
Ответ: 18
Определите наибольшее возможное количество элементов в множестве A .
Ответ: 7
Элементами множества А являются натуральные числа. Известно, что выражение
Определите наименьшее возможное количество элементов множества A.
Ответ: 1
Задания с отрезками на числовой прямой
Отрезки на числовой прямой:
На числовой прямой даны два отрезка: P=[44,48] и Q=[23,35].
Укажите наибольшую возможную длину отрезка А, для которого формула
тождественно ложна, то есть принимает значение 0 при любом значении переменной x.
Ответ: 4
✎ Решение 2 (программирование):
Внимание! этот способ подходит НЕ для всех заданий с отрезками!
Python:
def f(a1,a2,x): return((44 maxim: maxim=a2-a1 print(a1,a2, a2-a1) # сами точки отрезка и длина
PascalABC.net:
Отрезки на числовой прямой:
На числовой прямой даны два отрезка: P = [10,20] и Q = [30,40].
Укажите наибольшую возможную длину отрезка A, для которого формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Ответ: 10
Отрезки на числовой прямой:
На числовой прямой даны два отрезка: P = [3, 20] и Q = [6, 12].
Укажите наибольшую возможную длину отрезка A, для которого формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Ответ: 8
Далее возможно 2 способа решения.
✎ 2 способ:
После того, как мы избавились от импликации, имеем:
Отрезки на числовой прямой:
На числовой прямой даны два отрезка: P = [11, 21] и Q = [15, 40].
Укажите наибольшую возможную длину отрезка A, для которого формула
тождественно истинна, то есть принимает значение 1 при любом значении переменной x.
Ответ: 19
Задания с ДЕЛ
Поиск наибольшего А, известная часть Дел ∨ Дел = 1
Для какого наибольшего натурального числа А формула
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 8
Далее можно решать задание либо с помощью кругов Эйлера, либо с помощью логических рассуждений.
Решение с помощью логических рассуждений:
Решение с помощью кругов Эйлера:
Результат: 8
✎ Решение 2 (программирование):
Python:
for A in range(1,500): OK = 1 for x in range(1,1000): OK *= ((x % 40 == 0) or (x % 64 == 0))
Поиск наименьшего А, известная часть Дел ∧ ¬Дел = 1
Для какого наименьшего натурального числа А формула
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 3
Избавимся от импликации:
✎ Решение 2 (программирование). Язык Python, Pascal:
- Из общего выражения:
for A in range(1,50): OK = 1 for x in range(1,1000): OK *= (x % A == 0) 0)or (x mod 42 = 0)) = false then begin ok := 0; break; end; end; if (ok = 1) then begin print(A); break; end end; end.
Результат: 3
Для какого наименьшего натурального числа А формула
тождественно истинна (то есть принимает значение 1 при любом натуральном значении переменной х)?
Ответ: 285
✎ Решение 2 (программирование):
Python:
Из общего выражения: