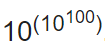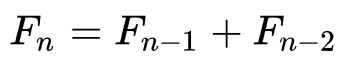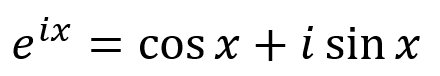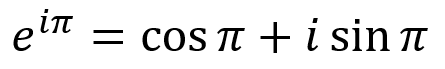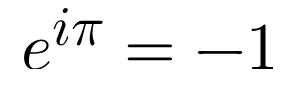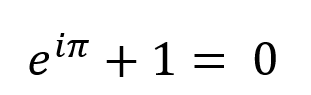красивая сумма какие еще числа знаете
Задача Яндекса про красивые числа
Для просмотра формул ваш браузер должен поддерживать MathML.
| Объявления | Последний пост | |
|---|---|---|
 | Запущен новый раздел «Задачки и головоломки» | 29.08.2019 00:42 |
 | Постдок позиция по математике в Гетеборге (Швеция) | 10.09.2021 19:11 |
 | Работа автором топиков и проектов на математическом треке Hyperskill | 24.09.2021 21:18 |
Это тестовое задание для учеников 8-9 классов, желающих поступить в математический лицей Яндекса. Для ее решения не нужно знать языков программирования, но можно пользоваться всеми техническими средствами. Время на решение задачи ограничено.
Назовём красивыми числа, в записи которых есть минимум две одинаковые цифры (например: 44, 505, 1101, 2324).
Сумма красивых чисел, меньших 100, равна 495 (11+22+33+44+55+66+77+88+99=495).
Найдите сумму красивых натуральных чисел, меньших 10000.
Я понимаю, что задачу уже решили на питоне и даже ответ есть. Но мне интересно, каким образом школьник может решить такую задачу меньше, чем за 45 минут?
После подсчета 4-значных чисел считаем трехзначные, двухзначные и однозначные. В конце концов все это складываем и вычитаем из суммы всех чисел.
Десяти минут и листочка бумаги с карандашом вполне хватит.
Красота и математика: 13 фантастических чисел, которые нас окружают
О числах и математических терминах, которые будут интересны не только математикам.
Нередко числа находятся с помощью красивых уравнений и формул. А еще они могут обладать математической красотой. Это значит, что их свойства ведут к непредсказуемому результату — привлекательному как визуально, так и интеллектуально.
Ниже мы обсудим 13 удивительных чисел и понятий, от бесконечности до золотого сечения, которые доказывают, что математика — тоже своего рода искусство.
13. Алеф-ноль ℵ0
Алеф-ноль — это наименьшее бесконечное кардинальное число. Возможно, вы подумаете: как же так? Ведь бесконечность — это всего лишь понятие, а не множество бесконечных чисел. В конце концов, если и существует бесконечность, которая больше другой бесконечности, то первая — уже определенно не бесконечность.
Сейчас разберемся. Предположим, у нас есть базовое представление о том, что такое бесконечность (см. пункт 12). Алеф-ноль — это множество натуральных чисел (0, 1, 2, 3 и т. д.). Это понятие (или число) велико по размеру и, в общем-то, бесконечно.
Что, если мы пересчитаем все натуральные числа два или три раза? После завершения первого множества мы получим числа, выходящие за рамки натуральных чисел по порядку. Итак, нам понадобится порядок чисел или порядковый номер. Следующее число после Алеф-ноль — это омега (ω). Затем идет ω + 1. Эти два последних числа — не кардинальные числа, а порядковые (ординалы): то есть они показывают положение элементов относительно горизонтальной оси. График ниже — их упрощенное представление.
Каждое множество чисел может представлять набор множеств натуральных чисел с мощностью ℵ0. Если добавить к первому множеству единицу — это не изменит количество элементов (вы даже можете просто изменить порядок, и у вас все равно останется мощность Алеф-ноль).
Это позволяет рассматривать их как порядковые величины (ординалы). Следовательно, первое порядковое трансфинитное число после набора — это то, что мы обсуждали выше — омега «ω». Интересно и то, что число ω + 1 необязательно больше ω — оно просто идет после него.
Да, возможно, это слишком для мгновенного понимания. Это то, о чем следует размышлять и к чему следует возвращаться. Поэтому ниже мы расписали все, что вам нужно знать:
А Алеф-ноль — всего лишь первый кардинал из огромного множества других «Алефов».
12. Бесконечность ∞
Это скорее идея или концепция, чем число. Этот символ часто называют лемнискатой. Прежде чем обсуждать характеристики и интересные факты о бесконечности, важно отметить, что число π (см. пункт 4) считается одной из ее форм. Конечно, под этим мы подразумеваем диапазон чисел после запятой в 3,14159… Вот почему бесконечность — это понятие, а не то, что можно выразить количественно. Другой пример: прекрасное поле фракталов. Возьмем, к примеру, простую снежинку Коха, которую можно разделить на бесконечно малые «хлопья» одинаковой формы.
Интересно и то, что, когда мы думаем о бесконечности, мы представляем постоянно растущую меру, но она не расширяется и не становится больше. Она такая, какая есть.
Обсудим две простые темы, связанные с бесконечностью (те, которые не требуют мощной мозговой активности):
Верно ли, что 0,99999 = 1?
Учитывая, что после запятой у нас есть девятки, которые стремятся к бесконечности, мы можем предположить, что 0,99999 приблизительно равно 1. Но существует и алгебраическое доказательство:
10x = 9,9999
Если вычесть x с каждой стороны, то получим:
9x = 9
Разделим обе стороны на 9 и получим, что:
x = 1
Немного странно, вы не находите?
Любое число, вычтенное из самого себя, даст ноль. Но ведь бесконечность — это не число. Значит, попробуем провести «тест»:
Добавим по 1 с каждой стороны:
Зная, что ∞ + 1 = ∞, упростим уравнение:
В школе нас также учат, что мы не можем делить на 0. Нам говорят, что 1 : 0 не имеет смысла. Что ж, это утверждение нельзя назвать неверным, но в то же время оно не отражает всей истины. Просто подумайте: если вы разделите 1 яблоко на 0 человек, сколько людей вам понадобится, чтобы съесть фрукт? Это форма бесконечности, которая никогда не разрушается.
Итак, получается 1 : 0 = ∞. Тогда почему нас учат, что результат не определен и не имеет смысла?
Итоговая таблица для вычислений с бесконечностью:
Буква i обозначает мнимое число. Это такое число, квадрат которого дает отрицательный результат. Это не то, о чем мы обычно думаем при возведении чисел в квадрат, потому что мы знаем, что умножение двух одинаковых чисел всегда дает положительный результат. Но это не мешает нам создать аксиому, которая бы изменила правила игры. Мы называем их воображаемыми, потому что их просто не должно быть.
Концепция мнимых чисел проста. Мы представляем, что они существуют. Чем они полезны? Мы можем решать уравнения, для которых нужен квадратный корень из отрицательного числа.
x 2 + 1 = 0
x = ± i
Есть и другое использование мнимых чисел: их объединяют с натуральными для получения комплексных чисел (например, 7i + 12), а также используют в электричестве.
10. Гугол
Гугол — это число в десятичной системе счисления, который изображается единицей со 100 нулями. И вот так оно выглядит: 10, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000, 000. Или:
А еще его можно представить в виде факториала 70! — то есть 70 x 69 x 68 x 67 x 66 x 65 x 64 x 63 x 62 x 61 x 60 x 59… х 1
Чтобы еще больше вас запутать, существует число под названием «гуголплекс». Это 10 в степени гугол:
Интересный факт: название компании Google представляет собой неправильное написание числа. Хитроумный способ назвать поисковую систему. Число в основном используется в астрономических исследованиях, в частности, в альтернативе теории Большого Взрыва — в Большом замораживании.
9. Цифра 9
Любимое число всех маркетологов (вспомните ценники) и красивое визуально и математически. В геометрии оно часто прячется во многих местах. Например, возьмем круг:
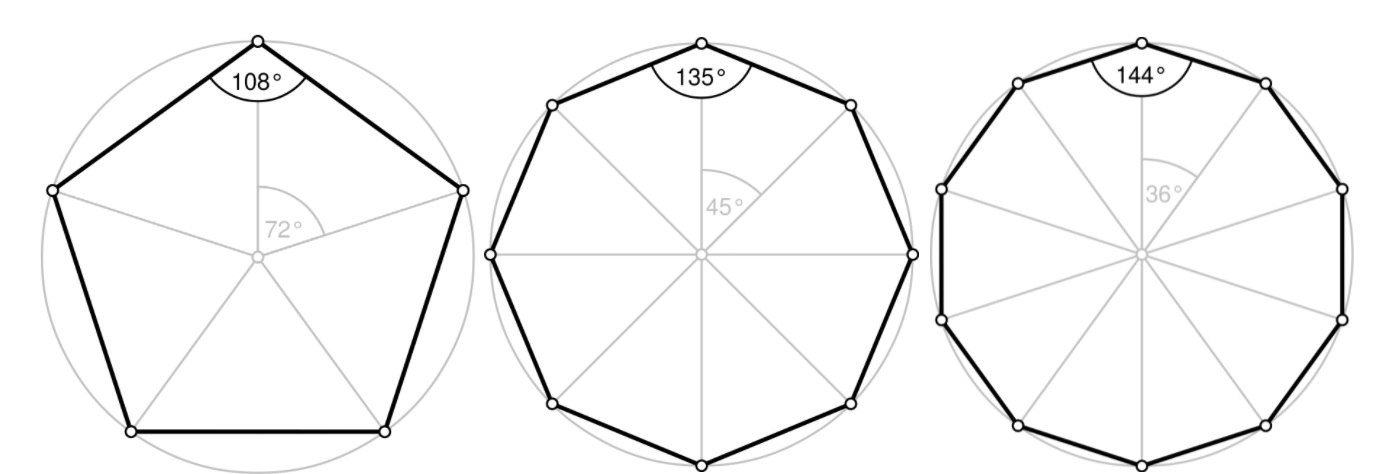
Еще несколько фигур с обозначением углов:
Слева направо: Пентагон, Октагон, Декагон.
Отвлечемся от геометрии. Если сложить цифры, которые предшествуют девяти, то получим 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 = 36. И вновь: 3 + 6 = 9
Если умножить цифры, предшествующие 9, на девять и сложить их элементы, сумма будет всегда равна 9. А вот и примеры:
Разделив цифры на 9, мы всегда получим одну и ту же цифру, повторяющуюся до бесконечности:
8. Число 73
Если вы фанат «Теории Большого взрыва», то, должно быть, вы помните, как Шелдон Купер объяснял, почему 73 — идеальное число:
«Самое замечательное число — 73. Вы, скорее всего, теряетесь в догадках почему. 73 — это 21-ое простое число. Его зеркальное отражение 37 является 12-ым, чье отражение 21 является результатом умножения, не упадите, 7 и 3».
«В двоичной системе 73 — еще палиндром. 1001001, что справа налево читается, как 100100».
Все эти цитаты — из 10 серии 4-го сезона сериала, которая, по определенному стечению обстоятельств, ялвяется 73-м эпизодом сериала (а еще годом рождения Джима Парсонса, актера, сыгравшего Шелдона).
7. Число Эйлера
Названное в честь Леонарда Эйлера, e — иррациональное число и основание натуральных логарифмов. Интересно, что число Эйлера известно с точностью до 1 триллиона цифр. А найти его можно с помощью этой формулы:
Когда n приближается к бесконечности, мы получаем более ясное представление о значении e. Когда n = 100000, e = 2,71827.
Еще одно удивительное свойство e — его наклон является его же значением. Оно также используется в финансах для расчета сложных процентов.
6. Последовательность Фибоначчи
Леонардо Боначчи, также известный как Фибоначчи (это прозвище, означающее «сын Боначчи»), создал одну из самых увлекательных последовательностей в нашей вселенной. И для этого он использовал простые методы сложения, наблюдая за популяциями кроликов.
Несмотря на то, что есть несколько свидетельств, которые говорят о том, что индийские математики вывели последовательность намного раньше, предлагаем придерживаться широко признанного факта, что ее автор — Фибоначчи.
Получить числа Фибоначчи можно с помощью простой формулы для n > 2:
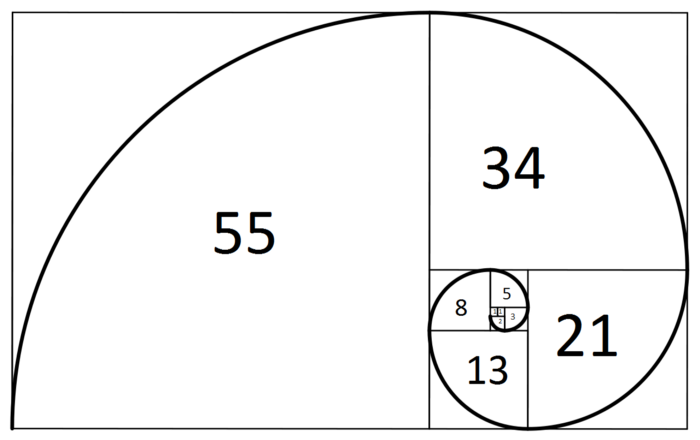
Так, мы получаем последовательность, которая уходит в бесконечность:
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,….
Ее прелесть в том, что она связана с природой. Например, ее можно обнаружить в цветении артишока и некоторых цветов вроде ромашек.
А что насчет Галактики? Гэри Б. Мэйснер выдвинул интересное и фактически обоснованное предположение, согласно которому размеры Земли и Луны находятся в соотношении Фи, образуя Треугольник, основанный на 1,618.
Но что такое Фи, и что за 1,618?
Если взять два любых последовательных числа в последовательности, их отношение (Xn / Xn-1) приблизится к 1,618. Это число называется Фи — в честь древнегреческого скульптора и архитектора Фидия — или «золотым числом»:
317 811 : 196 418 = 1,61803
Стремясь к бесконечности, значения отношений приближаются к 1,618.
5. Число 23
Наверное, многие видели фильм «Роковое число 23», в котором Джим Керри играет Уолтера Спэрроу — человека, который становится одержимым числом 23, после того как читает о нем в книге. Считается, что это число таинственным образом совпадает со многими событиями по всему миру, и, хотя это можно назвать наглядным примером Апофении, все-таки интересно перечислить некоторые «случайности»:
4. Пи (π) и Тау (τ)
Знаменитое иррациональное число, представляющее отношение длины окружности к ее радиусу. Сложно найти человека, который никогда его не видел.
Если мы нарисуем круг диаметром 1, тогда длина окружности будет равна 3,14159… что просто обозначается буквой π. Это длина окружности по диаметру.
А теперь к интересным свойствам:
А причем здесь Тау? Некоторые математики спорят над «полезностью» π и предлагают использовать вместо него тау (τ), которое равно 2π. По их словам, оно лучше подходит для вычисления кругов. Если вникнуть в детали, интуиция их не подводит. Но разве можно не любить π?
Кстати, ежегодно 14 марта отмечается день числа Пи (дата в США пишется в виде MM / DD — получается, 3/14).
3. Тождество Эйлера
А вот и главная причина, по которой в заголовке статьи фигурирует слово «красота». Сочетание красивейших математических концепций обычно дает простые результаты. Но для начала вспомним, о каких концепциях идет речь и как мы собираемся их объединить:
Но как это вышло?
Если переместить приведенную выше формулу Эйлера на комплексную плоскость (с настоящими и мнимыми числами), мы получим окружность. Включив в уравнение радиус r, мы сможем преобразовать точки в другую форму, например, возведя re в степень ix.
Если мы предположим, что x = π, то получим следующее:
Мы можем вновь изменить это уравнение, чтобы сделать его более красивым, и добавить еще одно простое число:
Это число, также известное как Постоянная Капрекара, имеет отличительную особенность. Вы поймете, какую, когда выполните следующие шаги:
Если вы будете повторять эти шаги, вы всегда будете получать 6174 — и это настоящая загадка.
Почему всегда выходит 6174, независимо от того, с каких чисел вы начнете? Давайте разберемся.
Возьмем, к примеру, 2714:
Теперь, когда мы получили 6174, мы больше не сдвинемся с этой точки. Потому что 7641-1467 = 6174.
А еще 6174 — число Харшада. Это значит, что оно делится на сумму его составляющих: 6174 / (6 + 1 + 7 + 4) = 6174/18 = 343.
1. Золотое сечение
Пожалуй, это самое важное соотношение в мире. Напоминаем: его вывели греки. А вот список его основных характеристик:
Бонус
На самом деле самое большое число из существующих — 40. А вот и доказательство:
Красота чисел. Антипростые числа
У числа 60 двенадцать делителей: 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60
Все знают об удивительных свойствах простых чисел, которые делятся только на самих себя и на единицу. Эти числа исключительно полезны. Относительно большие простые числа (примерно от 10 300 ) используются в криптографии с открытых ключом, в хеш-таблицах, для генерации псевдослучайных чисел и т.д. Кроме огромной пользы для человеческой цивилизации, эти особенные числа поразительно красивы:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199.
Все остальные натуральные числа больше единицы, которые не являются простыми, называются составными. У них несколько делителей. Так вот, среди составных чисел выделяется особая группа чисел, которые можно назвать «суперсоставными» или «антипростыми», потому что у них особенно много делителей. Такие числа почти всегда являются избыточными (кроме 2 и 4).
Избыточными называются положительное целое число N, у которого сумма собственных делителей (кроме N) превышает N.
Например, у числа 12 сразу шесть делителей: 1, 2, 3, 4, 6, 12.
Это избыточное число, потому что
Неудивительно, что именно число 12 используется в огромном количестве практических областей, начиная с религии: 12 богов в греческом пантеоне и столько же в пантеоне скандинавских богов, не считая Одина, 12 учеников Христа, 12 ступеней колеса буддистской сансары, 12 имамов в исламе и т.д. Двенадцатиричная система счисления — одна из самых удобных на практике, поэтому её используют в календаре, чтобы разделить год на 12 месяцев и 4 времени года, а также чтобы разделить день и ночь на 12 часов. Сутки составляют 2 круга часовой стрелки по кругу, разделённому на 12 отрезков; кстати, количество в 60 минут тоже выбрано неспроста — это ещё одно антипростое число с большим количеством делителей.
Удобная двенадцатиричная система используется в нескольких денежных системах, в том числе в древнерусских княжествах (12 полушек = 1 алтын = 2 рязанки = 3 новгородки = 4 тверских деньги = 6 московок). Как видим, большое количество делителей является критически важным качеством в условиях, когда монеты из разных систем нужно свести к одному номиналу.
Большие избыточные числа полезны в других областях. К примеру, возьмём число 5040. Это в каком-то смысле уникальное число, вот первые из списка его делителей:
То есть число 5040 делится на все простые числа от 1 до 10. Другими словами, если мы возьмём группу из 5040 людей или предметов, то мы можем поделить её на 2, 3, 4, 5, 6, 7, 8, 9 или 10 равных групп. Это просто великолепное число. Вот полный список делителей 5040:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 15, 16, 18, 20, 21, 24, 28, 30, 35, 36, 40, 42, 45, 48, 56, 60, 63, 70, 72, 80, 84, 90, 105, 112, 120, 126, 140, 144, 168, 180, 210, 240, 252, 280, 315, 336, 360, 420, 504, 560, 630, 720, 840, 1008, 1260, 1680, 2520, 5040
Чёрт побери, да мы можем поделить это число практически на что угодно. У него 60 делителей!
5040 — идеальное число для урбанистики, политики, социологии и т.д. На это обратил внимание ещё афинский мыслитель Платон 2300 лет назад. В своём фундаментальном труде «Законы» Платон писал, что в идеальной аристократической республике должно быть 5040 граждан, потому что такое количество граждан можно разделить на любое количество равных групп до десяти, без исключения. Соответственно, в такой системе удобно планировать управленческую и представительскую иерархию.
Конечно, это идеализм и утопия, но использование числа 5040 в самом деле исключительно удобно. Если в городе 5040 жителей, то его удобно делить на равные районы, планировать определённое количество объектов обслуживания для равного количества граждан, выбирать представительные органы на голосовании.
Такие высокосоставные, крайне избыточные числа и называются «антипростыми». Если мы хотим дать чёткое определение, то можно сказать, что антипростое число — такое положительное целое число, у которого больше делителей, чем у любого целого числа меньше его.
По такому определению, самым маленьким антипростым числом кроме единицы будет 2 (два делителя), 4 (три делителя). Далее следуют:
6 (четыре делителя), 12 (шесть делителей), 24, 36, 48, 60 (количество минут в часе), 120, 180, 240, 360 (количество градусов в круге), 720, 840, 1260, 1680, 2520, 5040, 7560, 10080, 15120, 20160, 25200, 27720, 45360, 50400
Именно эти числа удобно использовать в настольных играх с картами, фишками, деньгами и т.д. Например, они позволяют раздавать одинаковое количество карт, фишек, денег на разное количество игроков. По этой же причине их удобно использовать для составления классов школьников или студентов — например, чтобы разделить их на равное количество одинаковых групп для выполнения заданий. Для количества игроков в спортивной команде. Для количества команд в лиге. Для количество жителей в городе (о чём уже говорилось выше). Для административных единиц в городе, области, стране.
Как видно из примеров, многие из антипростых чисел уже де-факто используется в практических устройствах и системах счисления. Например, числа 60 и 360. Это было довольно предсказуемо, учитывая удобство наличия большого количества делителей.
О красоте антипростых чисел можно спорить. Если простые числа неоспоримо красивы, то антипростые числа, возможно, кому-то покажутся отвратительными. Но это поверхностное впечатление. Давайте посмотрим на них с другой стороны. Ведь фундаментом этих чисел являются простые числа. Именно из простых чисел, словно из строительных блоков, составлены составные числа, избыточные числа и венец творения — антипростые числа.
Основная теорема арифметики утверждает, что любое составное число можно представить как произведение нескольких простых множителей. Например,
При этом составное число не будет делиться больше ни на какое другое простое число, кроме своих простых множителей. Антипростые числа по определению отличаются максимальным произведением степеней простых множителей, из которых они состоят.
При этом их простые множители — это всегда последовательные простые числа. И степени в ряду простых множителей никогда не увеличиваются.
Так что в антипростых числах тоже есть своя особая красота.