косинус это какая ось
Как запомнить тригонометрический круг?
Лучший способ запомнить новую информацию в математике – это понять логику. Поэтому в этой статье я расскажу вам логику тригонометрического круга.

Дальше я сосредоточусь на том, как запомнить расположение чисел на осях синуса, косинуса, тангенса и котангенса.
Как запомнить какой точке какой синус и косинус соответствует?
— косинус равен абсциссе точки на числовой окружности
— синус равен ординате точки на числовой окружности.
Поэтому положительные значения косинусов и синусов расположены там же, где соответственно «иксы» и «игреки» положительны. Аналогично с отрицательными (на картинке ниже: оранжевые – плюс, синие – минус).
Шаг 2. Вспомните, что радиус тригонометрического круга равен \(1\), а это значит, что единицы и минус единицы на осях будут там, где круг пересечет оси.
Шаг 3. Так как ось котангенсов — это скопированная ось косинусов сдвинутая на 1 вверх, то и положительные отрицательные части осей там же где и на оси косинусов. Аналогично с осью тангенсов и синусов.
Шаг 4. Значение «\(1\)» на оси тангенсов и котангенсов находятся на одном уровне с единицей на оси косинусов и синусов. Аналогично, \(-1\) находятся на одном уровне с \(-1\) на оси синусов и косинусов.
Шаг 5. Дальше стоит понять, что \(±\frac<1><\sqrt<3>>\) находится ближе к \(0\), чем \(±\sqrt<3>\).
Шаг 6. \(±\sqrt<3>\) – это самые крайние точки, которые мы ставим на осях.
Опять же, подписывать все значения на тригонометрическом круге, и расставлять все числа на осях ни к чему. Достаточно нанести лишь те значения, которые надо найти.
Пример (ЕГЭ). Найдите значение выражения \(36\sqrt<6>\, tg\,\frac<π> <6>sin\,\frac<π><4>\).
Решение:
Геометрия. Урок 1. Тригонометрия
Смотрите бесплатные видео-уроки по теме “Тригонометрия” на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
Тригонометрия в прямоугольном треугольнике
Рассмотрим прямоугольный треугольник. Для каждого из острых углов найдем прилежащий к нему катет и противолежащий.
Синус угла – отношение противолежащего катета к гипотенузе.
sin α = Противолежащий катет гипотенуза
Косинус угла – отношение прилежащего катета к гипотенузе.
cos α = Прилежащий катет гипотенуза
Тангенс угла – отношение противолежащего катета к прилежащему (или отношение синуса к косинусу).
tg α = Противолежащий катет Прилежащий катет
Котангенс угла – отношение прилежащего катета к противолежащему (или отношение косинуса к синусу).
ctg α = Прилежащий катет Противолежащий катет
tg ∠ A = sin ∠ A cos ∠ A = C B A C
ctg ∠ A = cos ∠ A sin ∠ A = A C C B
tg ∠ B = sin ∠ B cos ∠ B = A C C B
ctg ∠ B = cos ∠ B sin ∠ B = C B A C
Тригонометрия: Тригонометрический круг
Тригонометрия на окружности – это довольно интересная абстракция в математике. Если понять основной концепт так называемого “тригонометрического круга”, то вся тригонометрия будет вам подвластна. В описании к видео есть динамическая модель тригонометрического круга.
Тригонометрический круг – это окружность единичного радиуса с центром в начале координат.
Рассмотрим прямоугольный треугольник A O B :
cos α = O B O A = O B 1 = O B
sin α = A B O A = A B 1 = A B
Итак, косинус угла – координата точки A по оси x (ось абсцисс), синус угла – координата точки A по оси y (ось ординат).
Давайте рассмотрим еще один случай, когда угол α – тупой, то есть больше 90 ° :
Ещё одно замечание.
Синус тупого угла – положительная величина, а косинус – отрицательная.
Основное тригонометрическое тождество
sin 2 α + cos 2 α = 1
Данное тождество – теорема Пифагора в прямоугольном треугольнике O A B :
A B 2 + O B 2 = O A 2
sin 2 α + cos 2 α = R 2
sin 2 α + cos 2 α = 1
Тригонометрия: Таблица значений тригонометрических функций
Тригонометрия: градусы и радианы
Как перевести градусы в радианы, а радианы в градусы? Как и когда возникла градусная мера угла? Что такое радианы и радианная мера угла? Ищите ответы в этом видео!
Тригонометрия: Формулы приведения
Тригонометрия на окружности имеет некоторые закономерности. Если внимательно рассмотреть данный рисунок,
можно заметить, что:
sin 180 ° = sin ( 180 ° − 0 ° ) = sin 0 °
sin 150 ° = sin ( 180 ° − 30 ° ) = sin 30 °
sin 135 ° = sin ( 180 ° − 45 ° ) = sin 45 °
sin 120 ° = sin ( 180 ° − 60 ° ) = sin 60 °
cos 180 ° = cos ( 180 ° − 0 ° ) = − cos 0 °
cos 150 ° = cos ( 180 ° − 30 ° ) = − cos 30 °
cos 135 ° = cos ( 180 ° − 45 ° ) = − cos 45 °
cos 120 ° = cos ( 180 ° − 60 ° ) = − cos 60 °
Рассмотрим тупой угол β :
Для произвольного тупого угла β = 180 ° − α всегда будут справедливы следующие равенства:
sin ( 180 ° − α ) = sin α
cos ( 180 ° − α ) = − cos α
tg ( 180 ° − α ) = − tg α
ctg ( 180 ° − α ) = − ctg α
Тригонометрия: Теорема синусов
В произвольном треугольнике стороны пропорциональны синусам противолежащих углов.
a sin ∠ A = b sin ∠ B = c sin ∠ C
Тригонометрия: Расширенная теорема синусов
Отношение стороны к синусу противолежащего угла равно двум радиусам описанной вокруг данного треугольника окружности.
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R
Тригонометрия: Теорема косинусов
Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
a 2 = b 2 + c 2 − 2 b c ⋅ cos ∠ A
b 2 = a 2 + c 2 − 2 a c ⋅ cos ∠ B
c 2 = a 2 + b 2 − 2 a b ⋅ cos ∠ C
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с тригонометрией.
Тригонометрия: Тригонометрические уравнения
Это тема 10-11 классов.
Из серии видео ниже вы узнаете, как решать простейшие тригонометрические уравнения, что такое обратные тригонометрические функции, зачем они нужны и как их использовать. Если вы поймёте эти базовые темы, то вскоре сможете без проблем решать любые тригонометрические уравнения любого уровня сложности!
Тригонометрия простыми словами
Официальное объяснение тригонометрии вы можете почитать в учебниках или на других интернет сайтах, а в этой статье мы хотим объяснить суть тригонометрии «на пальцах».
Для удобства работы с тригонометрическими функциями был придуман тригонометрический круг, который представляет собой окружность с единичным радиусом (r = 1).
Тогда проекции радиуса на оси X и Y (OB и OA’) равны катетам построенного треугольника ОАВ, которые в свою очередь равны значениям синуса и косинуса данного угла.
Тангенс и котангенс получаются соответстсвенно из треугольников OCD и OC’D’, построенных подобно исходному треугольнику OAB.
Для упрощения обучения тригонометрическим функциям в школе используют только некоторые удобные углы в 0°, 30°, 45°, 60° и 90°.
Значения тригонометрических функций повторяются каждые 90° и в некоторых случаях меняя знак на отрицательный.
Достаточно запомнить значения некоторых важных углов и понять принцип повтора значений для бОльших углов.
Значения тригонометрических функций
для первой четверти круга (0° – 90°)
Принцип повтора знаков тригонометрических функций
Угол может быть как положительный, так и отрицательный. Отрицательный угол считается угол, откладываемый в противоположную сторону.
В виду того, что полная окружность составляет 360°, значения тригонометрических функций углов, описывающих одинаковое положение радиуса, РАВНЫ.
Для лучшего понимания и запоминания значений тригонометрических функций воспользуйтесь динамическим макетом тригонометрического круга ниже. Нажимая кнопки «+» и «–» значения угла будут увеличиваться или уменьшаться соответственно.
Тригонометрический круг
Углы в радианах
Чтобы закрепить свои знания и проверить себя, воспользуйтесь онлайн-тренажером для запоминания значений тригонометрических функций.
Синус, косинус
До сих пор мы измеряли углы только в градусах. Оказывается, есть и другая система измерения углов – радианы.
По определению, 1 радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу. Вот он, на рисунке.
Вспомним, что полный круг – это 360 градусов. Длина окружности равна 2πr. Составим пропорцию. Длина окружности так относится к длине дуги на нашем рисунке, как 360°- к величине угла, опирающегося на дугу на рисунке, то есть к углу в 1 радиан.
Слева в нашей пропорции углы, справа – длина полного круга и длина дуги на нашем рисунке.
Из этой пропорции получаем, что 360° = 2π радиан. Значит, полный круг – это 2π радиан. Тогда полкруга – это π радиан, четверть круга (то есть 90°) – это π/2 радиан.
Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот,
Любой угол, выраженный в градусах, можно перевести в радианы. И наоборот, 1 радиан приблизительно равен 57 градусов.
Нарисуем единичную окружность — то есть окружность с радиусом, равным единице, и с центром в начале системы координат. Той самой системы координат с осями OX и OY, в которой мы привыкли рисовать графики функций.
Договоримся отсчитывать углы от положительного направления оси ОХ против часовой стрелки.
Мы помним, что полный круг — это 360 градусов. Тогда точка с координатами (1;0) соответствует углу в 0 градусов. Точка с координатами (-1; 0) отвечает углу в 180 градусов, точка с координатами (0;1) — углу в 90 градусов. Каждому углу от нуля до 360 градусов соответствует точка на единичной окружности. Обратите внимание,что на нашем тригонометрическом круге углы отмечены и в градусах, и в радианах.
14. Свойства функций синуса, косинуса, тангенса
и котангенса и их графики
14.1. СВОЙСТВА ФУНКЦИИ y = sin x И ЕЕ ГРАФИК
График функции y = sin x (синусоида)

Свойства функции y = sin x

Объяснение и обоснование
Описывая свойства функций, мы будем чаще всего выделять такие их характеристики:
1) область определения; 2) область значений; 3) четность или нечетность; 4) периодичность; 5) точки пересечения с осями
координат; 6) промежутки знакопостоянства; 7) промежутки возрастания и убывания * ;8) наибольшее и наименьшее
З а м е ч а н и е. Абсциссы точек пересечения графика функции с осью Ох
(то есть те значения аргумента, при которых функция равна нулю) называют нулями функции.
Напомним, что значение синуса — это ордина-
та соответствующей точки единичной окружности
(рис. 79). Поскольку ординату можно найти для
любой точки единичной окружности (в силу того,
что через любую точку окружности всегда можно
провести единственную прямую, перпендикуляр-
ную оси ординат), то область определения функции
y = sin x — все действительные числа. Это можно за-
писать так: D (sin x) = R.
Для точек единичной окружности ординаты нахо-
дятся в промежутке [–1; 1] и принимают все значения
от –1 до 1, поскольку через любую точку отрезка [–1; 1]
оси ординат (который является диаметром единичной
окружности) всегда можно провести прямую, перпендикулярную оси орди-
нат, и получить точку окружности, которая имеет рассматриваемую орди-
нату. Таким образом, для функции y = sin x область значений: y ∈ [–1; 1].
Это можно записать так: E (sin x) = [–1; 1].
Как видим, наибольшее значение функции sin x равно единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окружности является точка A, то есть при
Наименьшее значение функции sin x равно минус единице. Это значение
достигается только тогда, когда соответствующей точкой единичной окружности является точка B, то есть
при
поэтому ее график симметричен относительно начала координат.
В § 13 было обосновано также, что синус — периодическая функция с наименьшим положительным периодом
k — любое натуральное число.
Чтобы найти точки пересечения графика функции с осями координат,
напомним, что на оси Oy значение x = 0. Тогда соответствующее значение
y = sin 0 = 0, то есть график функции y = sin x проходит через начало координат.
На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых sin x, то есть ордината соответствующей точки единичной окруж
ности, равна нулю. Это будет тогда и только тогда, когда на единичной окруж-
ности будут выбраны точки C или D, то есть при x = πk, k ∈ Z (см. рис. 79).
функции синус положительны (то есть ордината соответствующей точки
единичной окружности положительна) в I и II четвертях (рис. 80). Таким
образом, sin x > 0 при всех x ∈ (0; π), а также, учитывая период, при всех
x ∈ (2πk; π + 2πk), k ∈ Z.
Значения функции синус отрицательны (то есть ордината соответствую-
щей точки единичной окружности отрицательна) в III и IV четвертях, поэто-
Промежутки возрастания и убывания
Учитывая периодичность функции sin x с периодом T = 2π, достаточно
исследовать ее на возрастание и убывание на любом промежутке длиной
2π, например на промежутке
то при увеличении аргумента x (x 2 > x 1 ) ордината соответствующей точки единичной окружности увеличивается (то есть
sin x 2 > sin x 1 ), следовательно, на этом промежутке функция sin x возрастает. Учитывая периодичность функции sin x,
делаем вывод, что она такж е возрастает на каждом из промежутков
Если x ∈ 
окружности уменьшается (то есть sin x 2 1 ), таким образом, на этом промежутке функция sin x убывает. Учитывая
периодичность функции sin x, делаем вывод, что она также убывает на каждом из промежутков
Проведенное исследование позволяет обоснованно построить график функции y = sin x. Учитывая периодичность этой
функции (с периодом 2π), д о статочно сначала построить график на любом промежутке длиной 2π, на пример на
промежутке [–π; π]. Для более точного построения точек графика воспользуемся тем, что значение синуса — это ордината
соответствующей точки единичной окружности. На рисунке 82 показано построение графика функции y = sin x на
промежутке [0; π]. Учитывая нечетность функции sin x (ее график симметричен относительно начала координат), для
построения графика на промежутке [–π; 0] отображаем полученную кривую симметрич но относительно начала координат
Поскольку мы построили график на
промежутке длиной 2π, то, учитывая
периодичность синуса (с периодом 2π),
повторяем вид графика на каждом про-
межутке длиной 2π (то есть переносим па-
раллельно график вдоль оси Ох на 2πk,
где k — целое число).
Получаем график, который называется
З а м е ч а н и е. Тригонометрические функции широко применяются в ма тематике, физике и технике. Например,
множество процессов, таких как колебания струны, маятника, напряжения в цепи переменного тока и т. п.,
описываются функцией, которая задается формулой y = A sin (ωх + φ). Та кие процессы называют гармоническими
колебаниями. График функции y = A sin (ωx + φ) можно получить из синусоиды y = sin х сжатием или растяжением ее вдоль
координатных осей и параллельным пере носом вдоль оси Ох. Чаще всего гармоническое колебание является функцией
времени t. Тогда оно задается формулой y = A sin (ωt + φ), где А — амплитуда колебания, ω — частота, φ — начальная
фаза,
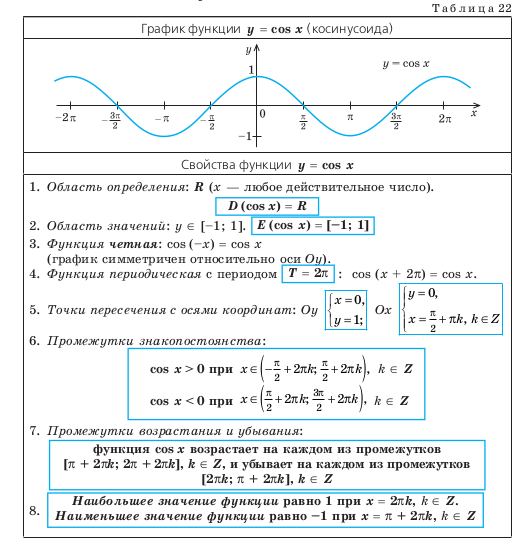
14.2. СВОЙСТВА ФУНКЦИИ y = cos x И ЕЕ ГРАФИК
Объяснение и обоснование
Напомним, что значение косинуса — это абсцис-
са соответствующей точки единичной окружности
(рис. 85). Поскольку абсциссу можно найти для лю-
бой точки единичной окружности (в силу того, что
через любую точку окружности, всегда можно про-
вести единственную прямую, перпендикулярную оси
абсцисс), то область определения функции y = cos x —
все действительные числа. Это можно записать так:
D (cos x) = R.
Для точек единичной окружности абсциссы нахо-
дятся в промежутке [–1; 1] и принимают все значе-
ния от –1 до 1, поскольку через любую точку отрезка [–1; 1] оси абсцисс (который является диаметром единичной
всегда можно провести прямую, перпендикулярную оси абсцисс, и получить
точку окружности, которая имеет рассматриваемую абсциссу. Следователь но, область значений функции y = cos x:
y ∈ [–1; 1]. Это можно записать так: E (cos x) = [–1; 1]. Как видим, наибольшее значение функции cos x равно единице. Это
зна чение достигается только тогда, когда соответствующей точкой единичной окружности является точка A, то есть при
x = 2πk, k ∈ Z. Наименьшее значение функции cos x равно минус единице. Это значение достигается только тогда, когда
соответствующей точкой единичной окруж ности является точка B, то есть при x = π + 2πk, k ∈ Z.
Как было показано в § 13, косинус — четная функция : cos (–x) = cos x, поэтому ее график симметричен относительно оси
Оу. В § 13 было обосновано также, что косинус — периодическая функция с наименьшим положительным периодом
T = 2π: cos (x + 2π) = cos x. Таким об разом, через промежутки длиной 2π вид графика функции cos x повторяется.
соответствующее значение y = cos 0 = 1. На оси Ox значение y = 0. Поэтому необходимо найти такие значения x, при
которых cos x, то есть абсцисса соответствующей точки единичной окружности будет равна нулю. Это будет тогда и только
тогда, когда на единичной окружности будут выбраны точки C или D, то есть при
Промежутки знакопостоянства. Как было обосновано в § 13, значения
функции косинус положительны (то есть абсцисса соответствующей точки
единичной окружности положительна) в I и IV четвертях (рис. 86). Следова-
тельно, cos x > 0 при x ∈ (-П/2; П/2) а также, учитывая период, при всех
Значения функции косинус отрицательны (то есть абсцисса соответству-
ющей точки единичной окружности отрицательна) во ІІ и ІІІ четвертях,
поэтому cos x
Промежутки возрастания и убывания
Учитывая периодичность функции cos x (T = 2π), достаточно исследовать
ее на возрастание и убывание на любом промежутке длиной 2π, например
на промежутке [0; 2π].
Если x ∈ [0; π] (рис. 87, а), то при увеличении аргумента x (x 2 > x 1 ) абсцисса соответствующей точки единичной
окружности уменьшается (то есть cos x 2 1 ), следовательно, на этом промежутке функция cos x убывает. Учитывая
периодичность функции cos x, делаем вывод, что она также убывает на каждом из промежутков [2πk; π + 2πk], k ∈ Z.
Если x ∈ [π; 2π] (рис. 87, б), то при увеличении аргумента x (x 2 > x 1 ) аб-
сцисса соответствующей точки единичной окружности увеличивается (то
есть cos x 2 >cos x 1 ), таким образом, на этом промежутке функция cos x
возрастает. Учитывая периодичность функции cos x, делаем вывод, что
она возрастает также на каждом из промежутков [π + 2πk; 2π + 2πk], k ∈ Z.
Проведенное исследование позволяет построить график функции y = cos x
аналогично тому, как был построен график функ-
ции y = sin x. Но график функции у = cos x можно
также получить с помощью геометрических преоб-
разований графика функции у = sin х, используя
Эту формулу можно обосновать, например, так.
Рассмотрим единичную окружность (рис. 88), отметим на ней точки