конечная последовательность команд по средством выполнения которой машина решает какую либо задачу
Урок 14
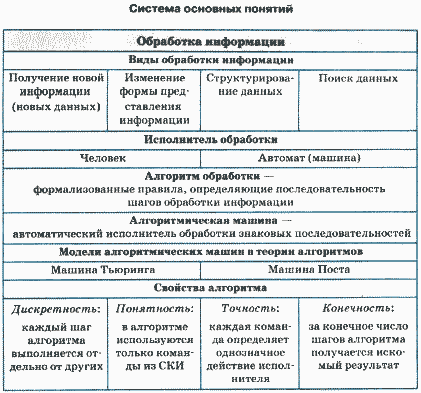
Обработка информации и алгоритмы
Содержание урока
Алгоритмические машины и свойства алгоритмов
Алгоритмические машины и свойства алгоритмов
В 30-х годах XX века возникает новая наука — теория алгоритмов. Вопрос, на который ищет ответ эта наука: для всякой ли задачи обработки информации может быть построен алгоритм решения? Но чтобы ответить на этот вопрос, надо сначала договориться об исполнителе, на которого должен быть ориентирован алгоритм.
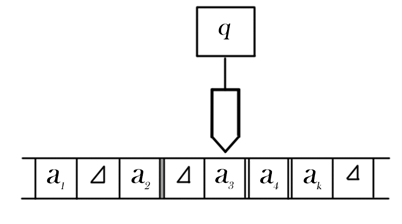
Английский ученый Алан Тьюринг предложил модель такого исполнителя, получившую название «машина Тьюринга». По замыслу Тьюринга, его «машина» является универсальным исполнителем обработки любых символьных последовательностей в любом алфавите. Практически одновременно с Тьюрингом (1936-1937 гг.) другую модель алгоритмической машины описал Эмиль Пост. Машина Поста работает с двоичным алфавитом и несколько проще в своем «устройстве». Можно сказать, что машина Поста является частным случаем машины Тьюринга. Однако именно работа с двоичным алфавитом представляет наибольший интерес, поскольку, как вы знаете, современный компьютер тоже работает с двоичным алфавитом. Подробнее с машиной Поста вы познакомитесь в следующем параграфе.
На основании моделей Тьюринга, Поста и некоторых других ученые пришли к выводу о существовании алгоритмически неразрешимых задач.
Язык программирования алгоритмических машин представляет собой описание конечного числа простых команд, которые могут быть реализованы в автоматическом устройстве.
Совокупность всех команд языка исполнителя называется системой команд исполнителя алгоритмов — СКИ.
Алгоритм управления работой алгоритмической машины представляет собой конечную последовательность команд, посредством выполнения которой машина решает задачу обра ботки информации.

• дискретностью (каждый шаг алгоритма выполняется отдельно от других);
• понятностью (в алгоритме используются только команды из СКИ);
• точностью (каждая команда определяет однозначное действие исполнителя);
• конечностью (за конечное число шагов алгоритма получается искомый результат).
Отметим разницу между понятиями «команда алгоритма» и «шаг алгоритма». Команда — это отдельная инструкция в описании алгоритма, а шаг алгоритма — это отдельное действие, которое исполнитель выполняет по команде. В циклических алгоритмах число шагов при выполнении алгоритма может быть больше, чем число команд в алгоритме, за счет повторного выполнения одних и тех же команд.
Следующая страница 
Алгоритмические машины и свойства алгоритмов
Урок 13. Информатика 10 класс (ФГОС)
В данный момент вы не можете посмотреть или раздать видеоурок ученикам
Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.
Получите невероятные возможности
Конспект урока «Алгоритмические машины и свойства алгоритмов»
В начале урока давайте вспомним, что такое алгоритм.
Алгоритм – это строгий порядок правил, которые определяют последовательность шагов обработки информации.
Ранее говорилось о том, что люди хотели создать машину, которая будет исполнять формальный алгоритм без помощи человека.
Для создания такой машины необходимо было выполнить некоторые условия: соответствие техническим требованиям; доскональное изучение работы алгоритма для обработки информации; разработка формализованного способа представления таких алгоритмов.
На этом уроке мы познакомимся с моделями алгоритмических машин в теории алгоритмов, а также вспомним свойства алгоритма.
Само понятие алгоритма исследовалось и совершенствовалось на протяжении многих лет. Но несмотря на все усилия, строгого определения понятия «алгоритм» не было. Поэтому начали появляться различные определения алгоритма. Но в тоже время все они были равнозначными.
Например, Андрей Николаевич Колмагоров, русский советский математик предложил следующее определение: алгоритм – это всякая система вычислений, выполняемых по строго определённым правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
А вот Андрей Андреевич Марков, советский математик, дал следующее определение для алгоритма. Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
Несмотря на то, что было много вариаций определения алгоритма, все они сводились к одним и тем же требованиям:
· алгоритм должен содержать конечное количество простых для выполнения команд, то есть удовлетворять требованию конечности записи;
· алгоритм должен выполнять конечное количество шагов при решении задачи, то есть удовлетворять требованию конечности действий;
· алгоритм должен быть единым для всех допустимых исходных данных, то есть удовлетворять требованию универсальности;
· алгоритм должен приводить к правильному по отношению к поставленной задачи решению, то есть удовлетворять требование правильности.
В 1930-х гг. возникает новая наука – теория алгоритмов. Она занимается изучением алгоритмов. Главным толчком для этого была работа Курта Гёделя, австрийского логика, математика и философа математики.
Он сформулировал и доказал теоремы о неполноте. Его работы были опубликованы в 1931 году. В теореме о неполноте символических логик было показано, что некоторые математические проблемы не могут быть решены при помощи алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.
Основной вопрос, на который ищет ответ теория алгоритмов таков: для всякой ли задачи обработки информации может быть построен алгоритм решения? Для того, чтобы найти ответ на этот вопрос нужно было изначально договориться об исполнителе, на которого будет ориентирован алгоритм.
Алан Тьюринг, английский математик, логик, криптограф, предложил в качестве исполнителя машину Тьюринга.
Машина использовалась для расшифровки сообщений. На основе открытого текста (стандартные отрывки текста, значение которых известно аналитику), машина Тьюринга искала возможные настройки, использованные для шифрования сообщений. Она производила ряд логических предположений, основываясь на открытом тексте, а затем находила противоречия, отбрасывала набор параметров и переходила к следующему. Таким образом, большая часть всевозможных наборов отсеивалась и для более тщательного анализа оставалось всего несколько вариантов. В 1940 году была запущена такая первая машина.
В 1936–1937 годах американский математик и логик, Эмиль Пост описал другую модель алгоритмической машины. Она называется машиной Поста.
Можно сказать, что эта машина является более упрощённой версией машины Тьюринга. Работа машины Поста основана на двоичном алфавите. Поэтому она представляет для нас наибольший интерес, так как все компьютеры работают с двоичным алфавитом. Более подробно с этой машиной мы познакомимся чуть позже.
Язык программирования алгоритмических машин представляет собой описание конечного числа простых команд, которые могут быть реализованы в автоматическом устройстве.
Таким образом, система команд исполнителя (СКИ) – это совокупность всех команд языка исполнителя.
Алгоритм управления работой алгоритмической машины – это конечная последовательность команд, с помощью которой машина решает задачу обработки информации.
Для алгоритма управления такой машиной существуют свои требования:
· Дискретность. Этот пункт говорит о том, что исполнитель должен выполнять каждый шаг отдельно от других;
· Понятность. В алгоритме используются только команды СКИ, предназначенные конкретно для этого исполнителя;
· Точность. Каждая команда должна конкретно говорить о действии, которое должен выполнять исполнитель;
· Конечность. Для исполнителя должно быть задано определённое (конечное) число шагов, после выполнения которых должен получится искомый результат.
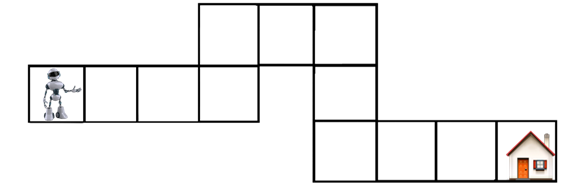
Рассмотрим пример. Нам необходимо записать алгоритм перемещения исполнителя Робот в клетку с домом. Данному исполнителю доступны три команды: вперёд, налево и направо.
Итак, наш алгоритм будет звучать следующим образом:
Учитель информатики
Сайт учителя информатики. Технологические карты уроков, Подготовка к ОГЭ и ЕГЭ, полезный материал и многое другое.
§ 2.1. Алгоритмы и исполнители
Информатика. 8 класса. Босова Л.Л. Оглавление
Ключевые слова:
2.1.1. Понятие алгоритма
Каждый человек в повседневной жизни, в учёбе или на работе решает огромное количество задач самой разной сложности. Сложные задачи требуют длительных размышлений для нахождения решения; простые и привычные задачи человек решает не задумываясь, автоматически. В большинстве случаев решение каждой задачи можно разбить на простые этапы (шаги). Для многих таких задач (установка программного обеспечения, сборка шкафа, создание сайта, эксплуатация технического устройства, покупка авиабилета через Интернет и т. д.) уже разработаны и предлагаются пошаговые инструкции, при последовательном выполнении которых можно прийти к желаемому результату.
Пример 1. Задача «Найти среднее арифметическое двух чисел» решается в три шага:
Пример 2. Задача «Внести деньги на счёт телефона» подразделяется на следующие шаги:
Пример 3. Этапы решения задачи «Нарисовать весёлого ёжика» представлены графически:
Нахождение среднего арифметического, внесение денег на телефонный счёт и рисование ежа — на первый взгляд совершенно разные процессы. Но у них есть общая черта: каждый из этих процессов описывается последовательностями кратких указаний, точное следование которым позволяет получить требуемый результат. Последовательности указаний, приведённые в примерах 1-3, являются алгоритмами решения соответствующих задач. Исполнитель этих алгоритмов — человек.
Алгоритм может представлять собой описание некоторой последовательности вычислений (пример 1) или шагов нематематического характера (примеры 2-3). Но в любом случае перед его разработкой должны быть чётко определены начальные условия (исходные данные) и то, что предстоит получить (результат). Можно сказать, что алгоритм — это описание последовательности шагов в решении задачи, приводящих от исходных данных к требуемому результату.
В общем виде схему работы алгоритма можно представить следующим образом (рис. 2.1).
Алгоритмами являются изучаемые в школе правила сложения, вычитания, умножения и деления чисел, многие грамматические правила, правила геометрических построений и т. д.
Анимации «Работа с алгоритмом» (193576), «Наибольший общий делитель» (170363), «Наименьшее общее кратное» (170390) помогут вам вспомнить некоторые алгоритмы, изученные на уроках русского языка и математики (http://sc.edu.ru/).
Пример 4. Некоторый алгоритм приводит к тому, что из одной цепочки символов получается новая цепочка следующим образом:
Получившаяся таким образом цепочка является результатом работы алгоритма.
Так, если исходной была цепочка А#В, то результатом работы алгоритма будет цепочка #А1В2, а если исходной цепочкой была АБВ@, то результатом работы алгоритма будет цепочка БА@В2.
2.1.2. Исполнитель алгоритма
Каждый алгоритм предназначен для определённого исполнителя.
Исполнитель — это некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Различают формальных и неформальных исполнителей. Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Неформальный исполнитель может выполнять команду по-разному.
Рассмотрим более подробно множество формальных исполнителей. Формальные исполнители необычайно разнообразны, но для каждого из них можно указать следующие характеристики: круг решаемых задач (назначение), среду, систему команд и режим работы.
Круг решаемых задач. Каждый исполнитель создаётся для решения некоторого круга задач — построения цепочек символов, выполнения вычислений, построения рисунков на плоскости и т. д.
Среда исполнителя. Область, обстановку, условия, в которых действует исполнитель, принято называть средой данного исполнителя. Исходные данные и результаты любого алгоритма всегда принадлежат среде того исполнителя, для которого предназначен алгоритм.
Система команд исполнителя. Предписание исполнителю о выполнении отдельного законченного действия называется командой. Совокупность всех команд, которые могут быть выполнены некоторым исполнителем, образует систему команд данного исполнителя (СКИ). Алгоритм составляется с учётом возможностей конкретного исполнителя, иначе говоря, в системе команд исполнителя, который будет его выполнять.
Режимы работы исполнителя. Для большинства исполнителей предусмотрены режимы непосредственного управления и программного управления. В первом случае исполнитель ожидает команд от человека и каждую поступившую команду немедленно выполняет. Во втором случае исполнителю сначала задаётся полная последовательность команд (программа), а затем он выполняет все эти команды в автоматическом режиме. Ряд исполнителей работает только в одном из названных режимов.
Рассмотрим примеры исполнителей.
Пример 5. Исполнитель Черепашка перемещается на экране компьютера, оставляя след в виде линии. Система команд Черепашки состоит из двух команд:
Запись Повтори k [ … ] означает, что последовательность команд в скобках повторится k раз.
Подумайте, какая фигура появится на экране после выполнения Черепашкой следующего алгоритма.
Повтори 12 [Направо 45 Вперёд 20 Направо 45]
Пример 6. Система команд исполнителя Вычислитель состоит из двух команд, которым присвоены номера:
1 — вычти 1
2 — умножь на 3
Первая из них уменьшает число на 1, вторая увеличивает число в 3 раза. При записи алгоритмов для краткости указываются лишь номера команд. Например, алгоритм 21212 означает следующую последовательность команд:
С помощью этого алгоритма число 1 будет преобразовано в 15: ((1 • 3 — 1) • 3-1) • 3 = 15.
Пример 7. Исполнитель Робот действует на клетчатом поле, между соседними клетками которого могут стоять стены. Робот передвигается по клеткам поля и может выполнять следующие команды, которым присвоены номера:
1 — вверх
2 — вниз
3 — вправо
4 — влево
При выполнении каждой такой команды Робот перемещается в соседнюю клетку в указанном направлении. Если же в этом направлении между клетками стоит стена, то Робот разрушается.
Что произойдёт с Роботом, если он выполнит последовательность команд 32323 (здесь цифры обозначают номера команд), начав движение из клетки А? Какую последовательность команд следует выполнить Роботу, чтобы переместиться из клетки А в клетку В, не разрушившись от встречи со стенами?
При разработке алгоритма:
Можно сказать, что алгоритм — модель деятельности исполнителя алгоритмов.
2.1.3. Свойства алгоритма
Не любая инструкция, последовательность предписаний или план действий может считаться алгоритмом. Каждый алгоритм обязательно обладает следующими свойствами: дискретность, понятность, определённость, результативность и массовость.
Свойство дискретности означает, что путь решения задачи разделён на отдельные шаги (действия). Каждому действию соответствует предписание (команда). Только выполнив одну команду, исполнитель может приступить к выполнению следующей команды.
Свойство понятности означает, что алгоритм состоит только из команд, входящих в систему команд исполнителя, т. е. из таких команд, которые исполнитель может воспринять и по которым может выполнить требуемые действия.
Свойство определённости означает, что в алгоритме нет команд, смысл которых может быть истолкован исполнителем неоднозначно; недопустимы ситуации, когда после выполнения очередной команды исполнителю неясно, какую команду выполнять следующей. Благодаря этому результат алгоритма однозначно определяется набором исходных данных: если алгоритм несколько раз применяется к одному и тому же набору исходных данных, то на выходе всегда получается один и тот же результат.
Свойство результативности означает, что алгоритм должен обеспечивать получение результата после конечного, возможно, очень большого, числа шагов. При этом результатом считается не только обусловленный постановкой задачи ответ, но и вывод о невозможности продолжения по какой-либо причине решения данной задачи.
Свойство массовости означает, что алгоритм должен обеспечивать возможность его применения для решения любой задачи из некоторого класса задач. Например, алгоритм нахождения корней квадратного уравнения должен быть применим к любому квадратному уравнению, алгоритм перехода улицы должен быть применим в любом месте улицы, алгоритм приготовления лекарства должен быть применим для приготовления любого его количества и т. д.
Пример 8. Рассмотрим один из методов нахождения всех простых чисел, не превышающих некоторое натуральное число п. Этот метод называется «решето Эратосфена» по имени предложившего его древнегреческого учёного Эратосфена (III в. до н. э.).
Для нахождения всех простых чисел, не больших заданного числа n, следуя методу Эратосфена, нужно выполнить следующие шаги:
Более наглядное представление о методе нахождения простых чисел вы сможете получить с помощью размещённой в Единой коллекции цифровых образовательных ресурсов анимации «Решето Эратосфена» (180279).
Рассмотренная последовательность действий является алгоритмом, так как она удовлетворяет свойствам:
Рассмотренные свойства алгоритма позволяют дать более точное определение алгоритма.
Алгоритм — это предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
2.1.4. Возможность автоматизации деятельности человека
Разработка алгоритма — как правило, трудоёмкая задача, требующая от человека глубоких знаний, изобретательности и больших временных затрат.
Решение задачи по готовому алгоритму требует от исполнителя только строгого следования заданным предписаниям.
Пример 9. Из кучки, содержащей любое, большее трёх, количество каких-либо предметов, двое играющих по очереди берут по одному или по два предмета. Выигрывает тот, кто своим очередным ходом сможет забрать все оставшиеся предметы.
Рассмотрим алгоритм, следуя которому первый игрок наверняка обеспечит себе выигрыш.
Исполнитель может не вникать в смысл того, что он делает, и не рассуждать, почему он поступает так, а не иначе, т. е. он может действовать формально. Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека. Для этого:
Самое главное: Алгоритмы и исполнители
Исполнитель — некоторый объект (человек, животное, техническое устройство), способный выполнять определённый набор команд.
Формальный исполнитель одну и ту же команду всегда выполняет одинаково. Для каждого формального исполнителя можно указать: круг решаемых задач, среду, систему команд и режим работы.
Алгоритм — предназначенное для конкретного исполнителя описание последовательности действий, приводящих от исходных данных к требуемому результату, которое обладает свойствами дискретности, понятности, определённости, результативности и массовости.
Способность исполнителя действовать формально обеспечивает возможность автоматизации деятельности человека.
§ 9. Обработка информации и алгоритмы
Из курса основной школы вам известно:
Обработка информации, наряду с хранением и передачей, относится к основным видам информационных процессов.
Варианты обработки информации
Обработка информации производится каким-то субъектом или объектом (например, человеком или компьютером) в соответствии с определенными правилами. Будем его называть исполнителем обработки информации. Информация, которая подвергается обработке, представляется в виде исходных данных. На рисунке 2.2 в обобщенном виде представлен процесс обработки информации.
Рис. 2.2. Модель обработки информации
Можно привести множество примеров, иллюстрирующих схему на рис. 2.2.
Первый пример: ученик (исполнитель), решая задачу по математике, производит обработку информации. Исходные данные содержатся в условии задачи. Математические правила, описанные в учебнике, определяют последовательность вычислений. Результат — это полученный ответ.
Второй пример: перевод текста с одного языка на другой — это пример обработки информации, при которой не меняется ее содержание, но изменяется форма представления — другой язык. Перевод осуществляет переводчик по определенным правилам, в определенной последовательности.
Третий пример: работник библиотеки составляет картотеку книжного фонда. На каждую книгу заполняется карточка, на которой указываются все параметры книги: автор, название, год издания, объем и пр. Из карточек формируется каталог библиотеки, где эти карточки располагаются в строгом порядке. Например, в алфавитном каталоге карточки располагаются в алфавитном порядке фамилий авторов.
Четвертый пример: в телефонной книге вы ищете телефон нужной вам организации, например плавательного бассейна; или в том же библиотечном каталоге разыскиваете сведения о нужной вам книге. В обоих случаях исходными данными является информационный массив — телефонный справочник или каталог библиотеки, а также критерии поиска — название организации или фамилия автора и название книги.
Все эти виды обработки может выполнять как человек, так и компьютер. В чем состоит принципиальное различие между процессами обработки, выполняемыми человеком и машиной?
Если исполнителем обработки информации является человек, то правила обработки, по которым он действует, не всегда формальны и однозначны. Человек часто действует творчески, неформально. Даже однотипные математические задачи он может решать разными способами. Работа журналиста, ученого, переводчика и других специалистов — это творческая работа с информацией, которая выполняется ими не по формальным правилам.
Об алгоритмах
Для обозначения формализованных правил, определяющих последовательность шагов обработки информации, в информатике используется понятие алгоритма.
Из курса информатики основной школы вы знаете, что слово «алгоритм» произошло от имени выдающегося математика средневекового Востока Мухаммеда аль-Хорезми (780-850 гг. н. э.), описавшего еще в IX веке правила выполнения вычислений с многозначными десятичными числами. Правила сложения, вычитания, умножения столбиком, деления «уголком», которым вас учили в младших классах, — это алгоритмы аль-Хорезми.
Первоклассник, который не знает, что такое НОД, но умеет сравнивать целые числа и выполнять вычитание, сможет исполнить алгоритм. Действовать при этом он будет формально.
Такой формализованный алгоритм легко запрограммировать для современного компьютера. Мечта создать машину — автоматическое устройство, которое сможет без вмешательства человека производить расчеты, появилась очень давно. Для ее реализации требовались не только технические возможности, но и глубокое понимание сущности алгоритмов обработки информации и разработка формализованного способа представления таких алгоритмов.
Алгоритмические машины и свойства алгоритмов
В 30-х годах XX века возникает новая наука — теория алгоритмов. Вопрос, на который ищет ответ эта наука: для всякой ли задачи обработки информации может быть построен алгоритм решения? Но чтобы ответить на этот вопрос, надо сначала договориться об исполнителе, на которого должен быть ориентирован алгоритм.
Английский ученый Алан Тьюринг (1912-1954) предложил модель такого исполнителя, получившую название «машина Тьюринга». По замыслу Тьюринга, его «машина» является универсальным исполнителем обработки любых символьных последовательностей в любом алфавите. Практически одновременно с Тьюрингом (1936-1937 гг.) другую модель алгоритмической машины описал Эмиль Пост. Машина Поста работает с двоичным алфавитом и несколько проще в своем «устройстве». Можно сказать, что машина Поста является частным случаем машины Тьюринга. Однако именно работа с двоичным алфавитом представляет наибольший интерес, поскольку, как вы знаете, современный компьютер тоже работает с двоичным алфавитом. Подробнее с машиной Поста вы познакомитесь в следующем параграфе.
На основании моделей Тьюринга, Поста и некоторых других ученые пришли к выводу о существовании алгоритмически неразрешимых задач.
Язык программирования алгоритмических машин представляет собой описание конечного числа простых команд, которые могут быть реализованы в автоматическом устройстве.
Совокупность всех команд языка исполнителя называется системой команд исполнителя алгоритмов — СКИ.
Алгоритм управления работой алгоритмической машины представляет собой конечную последовательность команд, посредством выполнения которой машина решает задачу обработки информации.
Отметим разницу между понятиями «команда алгоритма» и «шаг алгоритма». Команда — это отдельная инструкция в описании алгоритма, а шаг алгоритма — это отдельное действие, которое исполнитель выполняет по команде. В циклических алгоритмах число шагов при выполнении алгоритма может быть больше, чем число команд в алгоритме, за счет повторного выполнения одних и тех же команд.