кодирование появляется при передаче каких сообщений
Кодирование и Шифрование
В наш век интернет-технологий, когда мы доверяем все свои данные интернет-сервисам, нужно знать и понимать, как они их хранят и обрабатывают.
Но зачем это вообще нужно знать? Чтобы попросту не попасть в ситуацию, когда ваши личные данные, пароли от аккаунтов или банковских карт окажутся в руках мошенников. Как говорится: «Доверяй, но проверяй»
Важные аспекты в хранении данных, будь то на внешних серверах или домашнем компьютере, – это прежде всего кодирования и шифрование. Но чем они отличаются друг от друга? Давайте разбираться!
Ни для кого не секрет, что компьютер может хранить информацию, но он не может хранить её в привычной для нас форме: мы не сможем просто так написать на флешки реферат, не можем нарисовать на жестком диске картинку так, чтобы её мог распознать компьютер. Для этого информацию нужно преобразовать в язык понятный компьютеру, и именно этот процесс называется кодированием. Когда мы нажимаем на кнопку на клавиатуре мы передаем код символа, который может распознать компьютер, а не сам символ.
Определения и различия
Кодирование – процесс преобразования доступной нам информации в информацию понятную компьютерную.
Шифрование – процесс изменения информации таким образом, чтобы её смогли получить только нужные пользователи.
Шифрование применялось и задолго до создания компьютеров и информатики как таковой. Но зачем? Цели её применения можно было понять из определения, но я опишу их ещё раз более подробно. Главные цели шифрования это:
конфиденциальность – данные скрыты от посторонних
целостность – предотвращение изменения информации
идентифицируемость – возможность определить отправителя данных и невозможность их отправки без отправителя
Оценить стойкость шифра можно с помощью криптографической стойкости.
Криптографическая стойкость – это свойство шифра противостоять криптоанализу, изучению и дешифровки шифра.
Криптостойкость шифра делится на две основные системы: абсолютно стойкие системы и достаточно стойкие системы.
Абсолютно стойкие системы – системы не подверженные криптоанализу. Основные критерии абсолютно стойких систем:
Ключи должны генерироваться для каждого сообщения отдельно
Генерация ключей независима
Длина ключа должна быть не меньше длины сообщения
К сожалению, такие системы не удобны в своём использовании: появляется передача излишней информации, которая требует мощных и сложных устройств. Поэтому на деле применяются достаточно стойкие системы.
Достаточно стойкие системы – системы не могут обеспечить полную защиту данных, но гораздо удобнее абсолютно стойких. Надежность таких систем зависит от возможностей крипто аналитика:
Количества перехваченных сообщений
Времени и вычислительных способностей
А также от вычислительной сложности шифра.
Вычислительная сложность – совокупность времени работы шифрующей функции, объема входных данных и количества используемой памяти. Чем она больше, тем сложнее дешифровать шифр.
История шифрования
Шифрование берет своё начало ещё из древних времен. Примерно 1300 лет до нашей эры был создан один из первых методов шифрования – Атбаш. Принцип шифрования заключается в простой подставке символов по формуле:, где:
n – количество символов в алфавите
i – порядковый номер символа.
С тех самых пор шифрование активно развивалось вместе с развитием нашей цивилизации
Хоть шифры и менялись, но их принцип нет – для расшифровки сообщения требуется ключ. В случае с Абашем ключом может считать последовательность порядковых номеров исходных символов, но этот ключ ещё надо как-то передать. Методы шифрования, которые используются сейчас, научились-таки передавать ключи по открытым и незащищённым каналам связи. Казалось бы, передача ключей шифрования по обычным каналам — это добровольное жертвование своими данными, но не всё так просто. Разберём это на примере популярного алгоритма шифрования «RSA», разработанного в 1977 году.
Первым делом выбирается два случайный простых числа, которые перемножаются друг на друга – именно это и есть открытый ключ.
К слову: Простые числа — это те числа, которые могут делиться без остатка либо на 1, либо на себя.
Длина таких чисел может быть абсолютно любая. К примеру, возьмем два простых числа 223 и 13. Их произведение 2899 – будет являться открытым ключом, который мы и будем передавать по открытому каналу связи. Далее нам необходимо вычислить функцию «Эйлера» для произведения этих чисел.
Функция Эйлера – количество натуральных чисел, меньших чем само число и, которые будут являть взаимно простыми числами с самим числом.
Возможно, звучит непонятно, но давайте это разберем на небольшом примере:
φ (26) [фи от двадцати шести] = какому-то числу чисел, которое всегда будет меньше 26, а сами числа должны иметь только один общий делитель единицу с 26.
1 – подходит всегда, идем дальше;
7 – только на 1 – подходит;
Общее количество таких чисел будет равно 12. А найти это число можно по формуле: φ(n*k) = (n-1)(k-1) в нашем случае 26 можно представить как 2 * 13, тогда получим φ(26) = φ(2 * 13) = (2-1)*(13-1) = 1 * 12 = 12
Теперь, когда мы знаем, что такое функция Эйлера и умеем её вычислять найдем её для нашего открытого ключа – φ(2899) = φ(223 * 13) =(223 – 1)*(13-1) = 222 * 12 = 2664
После чего нам нужно найти открытую экспоненту. Не пугайтесь, тут будет гораздо проще чем с функцией «Эйлера».
Открытая экспонента – это любое простое число, которое не делится на функцию Эйлера. Для примера возьмем 13. 13 не делится нацело на число 2664. Вообще открытую экспоненту лучше выбирать по возрастанию простым перебором, а не просто брать случайную. Так для нашего примера разумнее было бы взять число 5, но давайте рассмотрим на примере 13
e – открытая экспонента
mod – остаток отделения
В обоих случаях у нас получится число 205
На этом подготовка отправки сообщения успешно завершается и начинается самое веселое – отправка данных для дешифрования сообщения. На этом шаге мы отправляем открытый ключ и открытую экспоненту человеку, сообщение которого хотим получить. Предположим, что в этот момент наш ключ и экспоненту перехватили 3-е лица, но до нужного нам человека они всё так же дошли
Теперь этому человеку нужно отправить нам сообщение, для простоты предположим, что это какое-то число, например: 92. Для этого ему нужно отправить нам остаток от деления 92 в степени открытой экспоненты на открытый ключ – T ^ e mod n , где
T – шифруемый текст
e – открытая экспонента
mod – остаток от деления
Предположим, что и в этот раз сообщение перехватили, но нам оно всё так же дошло
С – зашифрованный текст
d – закрытая экспонента
mod – остаток от деления
235 ^ 205 mod 2899 = 92.
Вуаля, и мы имеет исходное число. Но, что насчет перехваченных сообщений? У злоумышленника есть сообщение, ключ и экспонента, но как мы помни для дешифровки ему ещё нужна секретная экспонента, она же секретный ключ, но для того, чтобы вычислить её, ему придется разложить исходный ключ 2899 на множители, а сделать это не так уж и просто, особенно когда вместо двух чисел 223 и 13, будут использовать числа длиной несколько десятков символов
Но ничто в мире не идеально, в том числе и этот метод.
Его первый недостаток – это подборка пары чисел для открытого ключа. Нам нужно не просто сгенерировать случайно число, но ещё и проверить на то простое ли оно. На сегодняшний нет методов, которые позволяют делать это сверх быстро.
Второй недостаток – так же связан с генерацией ключа. Как мы с вами помним: «ключи должны генерировать независимо от каких-либо факторов», но именно это правило нарушается, когда мы пытается сгенерировать строго простые числа.
Третий недостаток – подбор и перебор чисел для экспонент.
Четвертый – длина ключей. Чем больше длина, тем медленнее идет процесс декодирования, поэтому разработчики пытаются использовать наименьшие по длиннее ключи и экспоненты. Даже я акцентировал на это внимание, когда говорил, что лучше взять число 5, вместо 13 для открытой экспоненты. Именно из-за этого и происходит большая часть взломов и утечек данных
Но не стоит печалиться, ведь как я и говорил: криптография и шифрование развивается вместе с развитием цивилизации. Поэтому довольно скоро все мы будем шифровать свои данные с помощью Квантового шифрование.
Этот метод основывается на принципе квантовой суперпозиции – элементарная частица может сразу находится в нескольких положениях, иметь разную энергию или разное направление вращения одновременно. По такому принципу и работает передача ключей шифрования по протоколу BB-84.
Есть оптоволокно, по которому передаются единичные фотоны света. Мы, как отправитель может сгенерировать абсолютно любой двоичный ключ, по тому же принципу квантовой супер позиции, ну или использовать обычные генераторы псевдослучайных чисел. Допустим мы хотим передать ключ 101001011. Для этого нам нужно принять за обозначение какое положение фотона соответствует единице, а какое нулю. Представим, что вертикальное положение – это 1, а горизонтальное – 0. Если оставить все так, то от передачи ключей таким образом не будет никакого смысла, ведь тогда злоумышленник всегда сможет измерить фотон, получить его значение, создать и отправить точно такой же обратно человеку, которому мы хоти передать ключ. Поэтому были введены ещё два положение – диагональные. Предоставим вертикальную волну, или же значение 1 и отклоним её на 45 градусов влево. Это будет вторая единица. Вернемся обратно и отклоним на 45 градусов вправо – это будет второй 0.
Вернемся к нашему ключу 101001011. Мы случайным образом выбираем направление – обычное или диагональное. Для удобства присвоим обычному номер 1, а диагональному 2.
Давайте отправим ключ – 1(1), 0(2), 1(1), 0(1), 0(1), 1(2), 0(2), 1(1), 1(2). Теперь человеку, которому мы отправляем ключ, нужно точно так же, совершенно случайно, выбрать случайное направление.
Допустим он выбрал направления: 221111212. Поскольку есть всего 2 плоскости отправки: 1 и 2, они же называются: канонический и диагональный базис, то шанс того, что он выбрал правильные направления 50%.
Если он угадал базис – он получил верное значение, если нет – неверное. Учитывая его направления, он получил: 001000011. Теперь нужно отсеять неправильные значения: можно сделать это обменом базисов по любому, даже не защищенному, каналу связи. После этого у нас обоих останется ключ: 0100011. Теперь с помощью его мы можем передавать и кодировать сообщения по обычному методу шифрования.
Заключение
Причитав и разобрав эту статью, мы с вами узнали, чем отличается кодирование от шифрования, их историю с будущим, узнали каким должен быть идеальный шифр и немного поговорили про крипто анализ. Уже с этими знаниями, которые были предоставлены в этой статье, можно спокойно идти и делать какую-нибудь систему авторизации или пытаться взломать какой-то сайт, главное не перебарщивать.
Электронная библиотека
Информационный процесс кодирования информации встречается в нашей жизни на каждом шагу. Любое общение между людьми происходит именно благодаря тому, что они научились выражать образы, чувства и эмоции с помощью специально предназначенных для этого знаков и сигналов – звуков, жестов, букв и пр.
Одну и ту же информацию мы можем выразить разными способами.
Каким образом можно сообщить об опасности?
1. Если на вас напали, вы можете просто крикнуть «Караул!» (англичанин крикнет «Help me!»).
2. Если имеется прибор под высоким напряжением, то требуется оставить предупреждающий знак (рисунок черепа или молнии).
В каждом из этих примеров необходимо знать правило, по которому отображается информация, правило кодирования. Такое правило назовем кодом.
Код (фр. code – кодекс, свод законов). Начиная с середины XIX века это слово, помимо основного значения, означало книгу, в которой словам естественного языка сопоставлены группы цифр или букв.
Чаще всего кодирование – это процесс представления информации в виде знаков (поскольку дискретные сигналы воспринимать и обрабатывать проще, чем непрерывные).
Знак вместе с его смыслом называют символом.
Используемый для кодирования конечный набор отличных друг от друга знаков называется алфавитом. Существует множество алфавитов.
· алфавит кириллических букв <А, Б, В, Г, Д, Е, …>;
· алфавит латинских букв <А, В, С, D, E, F, …>;
· алфавит знаков зодиака;
· набор знаков азбуки Брайля для слепых;
· набор китайских идеограмм;
· набор знаков генетического кода <А, Ц, Г, Т>.
Важнейшие технические коды для кодирования текстов, записанных на естественных языках, возникли с появлением электрического телеграфа, например:
· набор знаков второго международного телеграфного кода (телекс).
Алфавит, состоящий из двух знаков, называют двоичным, а каждый знак из этого алфавита – двоичным знаком.
Кодирование используется для представления информации в виде, удобном для хранения и передачи.
Передача сообщений всегда осуществляется во времени. Процесс кодирования также требует определенного количества времени, которым зачастую нельзя пренебрегать. При кодировании могут ставиться определенные цели и применяться различные методы. Наиболее распространенные цели кодирования:
· экономность (уменьшение избыточности сообщения, повышение скорости передачи или обработки);
· надежность (защита от случайных искажений);
· сохранность (защита от нежелательного доступа к информации);
· удобство физической реализации (двоичное кодирование информации в ЭВМ);
· удобство восприятия (схемы, таблицы).
Одно и то же сообщение можно закодировать разными способами, то есть выразить на разных языках. В процессе развития человеческого общества люди выработали большое число языков кодирования. К ним относятся:
· разговорные языки (русский, английский, хинди и др., всего более 2000);
· язык мимики и жестов;
· язык рисунков и чертежей;
· языки науки (языки математики, химии и т. д.);
· языки искусства (языки музыки, живописи, скульптуры);
· специальные языки (эсперанто, морской семафор, азбука Морзе, азбука Брайля для слепых и т. д.);
Для получения исходных символов по кодам символов применяют процедуру декодирования. При этом обязательно соблюдение условия: код должен быть однозначным, то есть одному исходному знаку должен соответствовать точно один код и наоборот.
Кодирование – это представление сигнала в определенной форме.
Декодирование – это получение исходных символов по кодам символов.
Виды кодирования зависят от поставленной цели.
Кодирование по образцу – каждый знак дискретного сигнала представляется знаком или набором знаков того алфавита, в котором выполняется кодирование. Кодирование по образцу используется, например, для ввода информации в компьютер с целью ее внутреннего представления.
Для перевода символов, вводимых с клавиатуры, в числовой код, хранящийся в памяти компьютера, используется кодовая таблица ASCII (American Standard Code for Information Interchange – американский стандартный код для обмена информацией), в которой каждому символу алфавита, а также множеству специальных управляющих команд соответствует числовой код.
Криптографическое кодирование, или шифрование, используется тогда, когда нужно защитить информацию от несанкционированного доступа.
Существует два основных широко применяющихся сегодня способа криптографического кодирования: симметричное кодирование с закрытым ключом и асимметричное кодирование с открытым ключом. При симметричном кодировании с закрытым ключом для кодирования и декодирования данных применяется один и тот же ключ. Этот ключ должен быть по безопасным каналам доставлен стороне, осуществляющей декодирование, что делает шифрование с симметричным ключом уязвимым. Напротив, при шифровании с асимметричным ключом сторона, осуществляющая декодирование, публикует так называемый открытый ключ (public key), который применяется для кодирования сообщений, а декодирование осуществляется другим – закрытым ключом (private key), известным только принимающей стороне. Такая схема делает асимметричный способ кодирования высоконадежным. По этой причине в последнее время он приобрел массовую популярность.
Во множестве шпионских фильмов-боевиков основным вопросом при захвате агента противника было получение ключей к шифрам. Получение ключа давало возможность прочесть все перехваченные ранее сообщения и сразу получить множество полезной информации. Но эта возможность достижима только тогда, когда речь идет о симметричных ключах. Получение публичного асимметричного ключа в этом смысле не дает никаких преимуществ, поскольку открытый ключ позволяет кодировать сообщения, но не может применяться для их декодирования.
Оптимальное кодирование служит для устранения избыточности данных путем снижения среднего числа символов кодового алфавита, предназначенных для представления одного исходного символа. Оптимальное кодирование обычно используется в архиваторах. В большинстве современных программ, предназначенных для оптимального кодирования (сжатия) данных, применяются одни и те же базовые алгоритмы.
Статистическое кодирование базируется на предварительном вычислении частоты повторения одних и тех же кодов в сообщении и составлении таблицы кодирования, позволяющей оптимальным образом расположить результирующий код. Таблица кодирования в этом случае должна стать неотъемлемой частью закодированных данных (методы Хаффмена, Шэннона-Фано, арифметическое кодирование).
Словарное кодирование основано на нахождении повторяющихся последовательностей символов в сообщении (слов) и замене каждого повторяющегося слова ссылкой на его первое вхождение.
В этом случае вместе с закодированным сообщением необходимо хранить (передавать) словарь. К алгоритмам словарного кодирования относятся LZ77, LZ78, LZSS, LZW.
Во многих современных программах-архиваторах применяется последовательное (двухшаговое) использование методов статистического и словарного кодирования, позволяющее достигнуть наилучшей степени сжатия данных.
Помехозащищенное кодирование служит для передачи данных по каналам связи и учитывает возможность возникновения помех и связанного с этим искажения или утраты части данных. При помехозащищенном кодировании избыточность не снижается, а, наоборот, увеличивается, тем самым обеспечивается возможность определения факта потери или искажения информации. Существует два основных типа помехозащищенного кодирования:
· кодирование с фиксацией ошибок обладает сравнительно небольшой избыточ¬ностью, позволяющей зафиксировать на приемной стороне факт появления в сообщении ошибки. В случае обнаружения ошибки сообщение передается повторно;
· кодирование с коррекцией ошибок еще более избыточно, что позволяет не только обнаружить возникшую при передаче по каналу связи ошибку, но и исправить ее. Недостатком этого вида кодирования является значительное (примерно в 3 раза) увеличение объема передаваемых данных. По этой причине оно используется гораздо реже, чем кодирование с фиксацией ошибок.
Срочно?
Закажи у профессионала, через форму заявки
8 (800) 100-77-13 с 7.00 до 22.00
Кодирование для чайников, ч.1
Не являясь специалистом в обозначенной области я, тем не менее, прочитал много специализированной литературы для знакомства с предметом и прорываясь через тернии к звёздам набил, на начальных этапах, немало шишек. При всём изобилии информации мне не удалось найти простые статьи о кодировании как таковом, вне рамок специальной литературы (так сказать без формул и с картинками).
Статья, в первой части, является ликбезом по кодированию как таковому с примерами манипуляций с битовыми кодами, а во второй я бы хотел затронуть простейшие способы кодирования изображений.
0. Начало
Давайте рассмотрим некоторые более подробно.
1.1 Речь, мимика, жесты
1.2 Чередующиеся сигналы
В примитивном виде кодирование чередующимися сигналами используется человечеством очень давно. В предыдущем разделе мы сказали про дым и огонь. Если между наблюдателем и источником огня ставить и убирать препятствие, то наблюдателю будет казаться, что он видит чередующиеся сигналы «включено/выключено». Меняя частоту таких включений мы можем выработать последовательность кодов, которая будет однозначно трактоваться принимающей стороной.
1.3 Контекст
2. Кодирование текста
Текст в компьютере является частью 256 символов, для каждого отводится один байт и в качестве кода могут быть использованы значения от 0 до 255. Так как данные в ПК представлены в двоичной системе счисления, то один байт (в значении ноль) равен записи 00000000, а 255 как 11111111. Чтение такого представления числа происходит справа налево, то есть один будет записано как 00000001.
Итак, символов английского алфавита 26 для верхнего и 26 для нижнего регистра, 10 цифр. Так же есть знаки препинания и другие символы, но для экспериментов мы будем использовать только прописные буквы (верхний регистр) и пробел.
Тестовая фраза «ЕХАЛ ГРЕКА ЧЕРЕЗ РЕКУ ВИДИТ ГРЕКА В РЕЧКЕ РАК СУНУЛ ГРЕКА РУКУ В РЕКУ РАК ЗА РУКУ ГРЕКУ ЦАП».
2.1 Блочное кодирование
Информация в ПК уже представлена в виде блоков по 8 бит, но мы, зная контекст, попробуем представить её в виде блоков меньшего размера. Для этого нам нужно собрать информацию о представленных символах и, на будущее, сразу подсчитаем частоту использования каждого символа:
Кодирование передаваемых сообщений



В большинстве радиоэлектронных систем передача сообщения сопровождается кодированием. Поэтому рассмотрим подробнее данный вопрос.
Кодом называется правило однозначного преобразования элементарных символов алфавита А в символы алфавита В. Процесс такого преобразования называется кодированием, а обратный ему процесс, связанный с переходом от алфавита В к А, — декодированием.
Максимальное количество составных сигналов или комбинаций А/кода при основании т и значности n.
При двоичном полном коде
гдезначность n = log2N есть число разрядов или бит в одном составном сигнале или в одной кодовой комбинации.
Процесс передачи и приема кодовых комбинаций может сопровождаться ошибками, что связано с трансформацией одних элементарных символов в другие, например, в приеме вместо символа 1 символа 0 или наоборот. Коды, обнаруживающие и исправляющие ошибки, называются корректирующими. Такой код обязательно является неполным, т.е. имеющим число кодовых комбинаций меньше числа, определяемого согласно (1.6) или (1.7).
В любом корректирующем коде исправление ошибок достигается за счет его избыточности, т.е. путем добавления к смысловым символам контрольных. К таким кодам относятся, например, групповые или блоковые коды [24, 30].
В групповом корректирующем двоичном коде значностью п все символы разбиваются на две группы: информационные (смысловые) и контрольные (избыточные). Каждая кодовая комбинация или слово, состоящая из п бит, имеет к информационных и (п-к ) контрольных символов.
| Буква | Число в десятичной системе | Число в двоичной системе |
| А | ||
| Б | ||
| В | ||
| Г | ||
| Д | ||
| Е | ||
| Ж | ||
| З | ||
| И | ||
| Й | ||
| К | ||
| Л | ||
| М | ||
| Н | ||
| П | ||
| Р | ||
| С | ||
| Т | ||
| У | ||
| Ф | ||
| X | ||
| Ц | ||
| Ч | ||
| Ш | ||
| Щ | ||
| Ъ | ||
| Ы | ||
| Ь | ||
| Э | ||
| Ю | ||
| Я | ||
| Пробел | 1G0001 | |
| Точка |
Таким образом, в групповом коде из общего числа N = 2 n используютсятолько К= 2 к комбинаций. В целом групповой код обозначаетсякак (n, к).
Пусть имеется семь строк кодированной информации в один байт с последним битом контроля четности. Добавим к этим семи строкам восьмую и помимо проверки контроля четности по строкам будем производить проверку четности по столбцам (табл. 1.2), что позволит обнаружить одиночную ошибку не только в строке, но и в том или ином столбце.
В результате в 64-битовом блоке удастся обнаружить ошибочный бит, лежащий на пересечении строки и столбца, не отвечающих правилу четности. Найденный ошибочный бит подлежит исправлению. Таким образом, корректирующий код при 64-битовом блоке за счет небольшого увеличения его избыточности помимо свойства обнаружения ошибки приобретает дополнительное качество по исправлению одиночных ошибок в каждой из семи строк.
Другой простой, но весьма надежный метод обнаружения ошибки состоит в подсчете общего числа символов 1 и 0 в передаваемом сообщении и включении в конец этого сообщения полученного числа. В принятом сообщении вновь производится подсчет сумм 1 и 0. Расхождение данных сумм, называемых контрольными, в переданном и принятом сообщениях является признаком обнаружения ошибки.
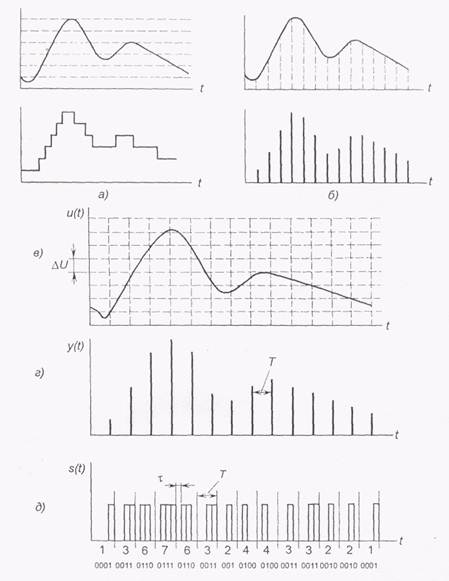
При кодировании сообщения необходимо его представление в дискретной форме (см. рис. 1.1,б). Поэтому рассмотрим, как аналоговый сигнал преобразовать в дискретный. Возможны три способа такого преобразования: путем квантования по уровню, по времени и одновременно по уровню и времени, и соответственно получение трех видов сигналов: релейного (рис. 1.3,а), импульсного (рис. 1.3,б) и цифрового (рис. 1.3,б). Заметим, что в релейном элементе сигнал на выходе меняется скачком при прохождении входным сигналом некоторого фиксированного значения. Поэтому сигнал со скачкообразным изменением амплитуды называется релейным (рис. 1.3,а).
Теперь вновь обратимся к рис. 1.3,в, поясняющему преобразование аналогового сообщения u(t) в цифровое s(t). Сначала произведем отсчеты функции u(t) через равные интервалы дискретизации Т.
В результате вместо аналогового сообщения u(t) получим цифровое s(f). На рис. 1.3,д показаны измеренные значения амплитуды сигнала в десятичной и двоичной системах счисления.
Временной шаг дискретизации устанавливается равным
Из (1.9) получим для скорости передаваемого сообщения, преобразованного в цифровую форму:
Именно такова скорость передачи речевых и иных сообщений в стандартном цифровом проводном канале связи.