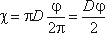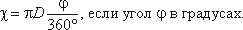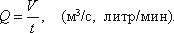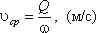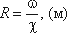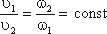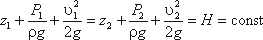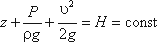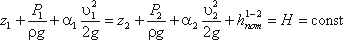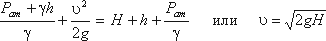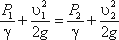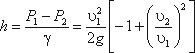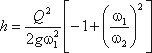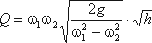какую скорость называют средней скоростью движения жидкости

Поток жидкости и его параметры

Поток жидкости — это часть неразрывно движущейся жидкости, ограниченная твердыми деформируемыми или недеформируемыми стенками, образующими русло потока. Потоки, имеющие свободную поверхность, называются безнапорными. Потоки, не имеющие свободной поверхности, называются напорными

Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.

Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.

Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

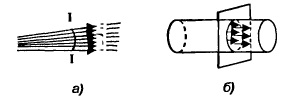
Рис. Векторы скорости потока жидкости (а) и живое сечение потока (б)

Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.

Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.

Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.

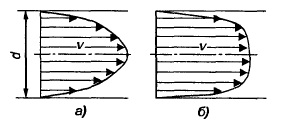
Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Рис. Распределение скоростей движения жидкости в живом сечении трубы при течении: а — турбулентном; б — ламинарном

Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:

Vcр = Sэ/d,
где Sэ — площадь эпюры местных скоростей; d — диаметр трубы

Объемный расход жидкости рассчитывается по формуле:

Q = Sэ*Мср,
где Q — площадь живого сечения потока.

Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.

Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.

Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.

Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.

Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.

Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.

Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.

Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.

Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.

Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.

Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:

Re = vd/V,
где Re — число Рейнольдса; v — средняя скорость потока; d — диаметр трубопровода; V — кинематическая вязкость жидкости.

Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:

Источник

Основные характеристики потока жидкости.

Поток жидкости.Под потоком жидкости подразумевается движение безразмерного множества отдельных частиц, которые движутся по своим траекториям. Как и в гидростатике, основной искомой величиной является величина гидростатического давления, а также значения скорости, расхода и т.п. при условии движения всех частиц жидкости.

Скорость течения потока. Под скорость движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении. В связи представлением о скорости потока необходимо ввести ряд определений скорости.

Локальная скорость течения.Локальной скоростью движения жидкости является скорость движения безразмерно малой частицы жидкости.

Средней скоростью течения.Под средней скоростью движения потока жидкости подразумевается суммарное передвижение всех частиц потока в одном направлении, проходящее через площадку перпендикулярную векторам скорости. Локальная и средняя скорость движения потока жидкости связаны выражением:

, (31)

где — локальная скорость; — площадь поперечного сечения движению потока.

Установившийся (стационарный) поток движение жидкости.Установившимся потоком движение жидкости является поток, скорость в котором не зависит от времени рис 2.2.6.

Переменный, установившийся (квазистационарный) поток движения жидкости.Квазистационарным установившимся потоком движения жидкости является поток, скорость в котором меняется в установленном порядке от времени, рис 2.2.8.

Неустановившийся (нестационарный) поток движение жидкости.Неустановившимся потоком движение жидкости является поток, скорость в котором зависит только от времени, рис 2.2.8.

Элементарная струйка. Понятие об элементарной струйке жидкости дает возможность рассматривать группу струек, движущихся совместно. Элементарна струйка (линяя тока) рис.2.2.9 может быть представлена как кривая, проходящая мгновенно совместно с такими же частицами, скорость которых направлены по касательной к этой кривой.

При этом установившееся движение можно представить как совокупность элементарных струек (линий тока), движущихся с равными скоростями частиц скользящими одна по другой. Линии тока в этом случае можно рассматривать как отдельные линии потока, к которым стремятся элементарные струйки при бесконечном уменьшении площадей их сечения. Такая совокупность движущихся струек образует поток жидкости.

Траектория движения частицы не является линией тока. В частном случае (стационарный режим движения) линия тока совпадает с траекторией и описывается функцией траектории.

Расход жидкости.Произведение площади элементарной струйку потока жидкости на величину локальной скорости движения U представляет некоторое количество жидкости. Это количество жидкости называется элементарным объемным расходом

. (32)

Определение расхода всего потока жидкости затрудняется не знанием закона распределения скоростей по сечению.

В этом случае можно записать:

(33)

Предполагая толкование средней скорости потока как выражение:

(34)

Исходя из выражения (34) можно записать:

(35)

В отдельных случаях секундный расход жидкости измеряют в весовых единицах, в кгс/сек. Такой элементарный расход называют весовым:

(36)

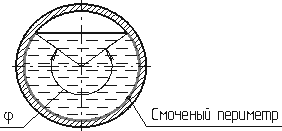
Смоченный периметр. Часть периметра поперечного сечения, образуемое твердыми стенками, входящее в контакт с потоком жидкости, называется смоченным периметром. Следовательно, при напорном движении смоченный периметр меньше полного периметра поперечного сечения

Гидравлический радиус. Гидравлический радиус представляют собой отношение площади поперечного сечения потока к его смоченному периметру П_см:

, (37)

где — площадь поперечного сечения; П_см смоченный периметр.

Эквивалентный диаметр.Эквивалентный диаметр используется, как правило, в вентиляционной технике. Эквивалентный диаметр равен четырем гидравлическим радиусам.

(38)

Источник

Основные параметры и режимы течения жидкости

Основными параметрами, характеризующими движение жидкости являются: площадь живого сечения S, расход жидкости Q и средняя скорость движенияv.

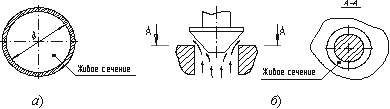
Площадь живого сечения.Живым сечением потока жидкости (рис. 8.1) называется сечение, которое в каждой своей точке нормально к векторам скоростей частиц жидкости.

Рис. 8.1. Живые сечения потока жидкости:

а– теоретическое сечение; б – практическое сечение;

в–эпюра скоростей в живом сечении по глубине потока

В практике чаще всего встречаются потоки жидкостей, живое сечение которых представляет собой поверхность, мало отличающуюся от плоскости.

Расход жидкости.Расходом жидкостиназывается количество жидкости, проходящее через данное живое сечениев единицу времени. Расход может измеряться в объемных или массовых единицах:

Средняя скорость движения жидкости. В общем случае скорости частиц в разных точках живого сечения будут различны. Если площадь эпюры частных скоростей F_э разделить на ширину потока жидкости H, то в соответствующем масштабе получим значение средней скорости движения жидкости, т.е.,

Это соотношение часто используется в практике для определения третьей неизвестной величины при двух известных, в частности, для определения средней скорости движения жидкости по расходу и площади живого сечения.

Основные режимы движения жидкости.В зависимости от того, остаются постоянными или изменяются те или иные параметры во времени и пространстве, режимы движения жидкости могут быть различными. Основными режимами движения жидкости являются:

– установившееся и неустановившееся;

– равномерное и неравномерное;

– напорное и безнапорное движение;

– неразрывное и кавитационное;

– ламинарное и турбулентное.

Установившееся и неустановившееся движение. Установившимся движениемназывается такой вид движения, при котором параметры, характеризующие движение, не изменяются во времени. Примером такого движения является истечение жидкости из емкости, в которой поддерживается постоянный уровень. При этом жидкость вытекает с постоянной скоростью, струя в пространстве занимает вполне определенное положение, давление в какой-либо точке А (рис. 8.2) остается неизменным. Если уровень в резервуаре не поддерживается постоянным, то перечисленные параметры будут переменными, Такое движение жидкости и называется неустановившимся.

Равномерное и неравномерное движение.Равномерным движением называется такой вид движения, при котором параметры, характеризующие это движение, не меняются по длине потока. Неравномерное движение, наоборот, характеризуется тем, что параметры движения потока будут переменными. Примером равномерного движения может служить движение жидкости в трубе постоянного диаметра при постоянном напоре. Неравномерное движение при тех же условиях будет, например, в конической трубе.

Рис. 8.2. Основные режимы движения жидкости:

а– установившееся; б – неустановившееся; в – равномерное; г – неравномерное;

д – напорное; е – безнапорное; ж – неразрывное; з – кавитационное;

и– ламинарное; к – турбулентное

Напорное и безнапорное движение.Напорным движением называется движение, при котором поток жидкости со всех сторон ограничен твердыми стенками. Примером такого движения является движение жидкости в трубопроводе за счет напора, создаваемого насосом. Напорное движение осуществляется за счет наличия разности давлений по длине трубопровода.

Безнапорное движение-это такое движение жидкости, при котором имеется свободная поверхность жидкости. Примером подобного движения является течение воды в реках, открытых каналах и др. Безнапорное движение происходит за счет разности уровней жидкости.

Неразрывное и кавитационное движение.Неразрывным движением называется такой вид движения, при котором жидкость движется сплошным потоком, образуя сплошную среду, заполняющую пространство. При движении газов неразрывность потока будет во всех случаях.

При движении капельных жидкостей неразрывность потока нарушается. Причиной этого может быть повышение температуры жидкости или понижение давления. В обоих случаях возможно выделение паров жидкости и растворенных вней газов. Когда давление парообразования становится равным внешнему давлению, в жидкости образуются пузыри и даже целые полости, заполненные парами или газами, которые расчленяют поток.

Давление парообразования, как уже отмечалось, зависит от температуры жидкости и характеризуется для воды следующими данными:

при t = 100 o C p_п = 760 мм рт. ст.;

Пузыри или полости с парами и газами, перемещаясь в жидкости или вместе с ней, попадают в узлы гидравлической системы с более низкой температурой или более высоким давлением. При этом пары жидкости мгновенно конденсируются, а газы снова растворяются в жидкости, в образовавшиеся пустоты с большой скоростью устремляются частицы жидкости. Это приводит к резкому повышению давления в этих местах (от 0,1 до 1 кПа), а также к местному повышению температуры (от 100 до 1500 o С). Рассмотренное явление носит названиекавитации. Кавитация вредна для гидравлических систем.

Ламинарное и турбулентное движение жидкости. Ламинарнымназывается струйчатое (или слоистое) течение без перемешивания частиц жидкости и без пульсации скорости и давления. При таком течении все линии тока жидкости вполне определяются формой русла. При ламинарном течении в трубе все линии тока направлены параллельно оси трубы. Ламинарное течение является упорядоченным, строго установившимся течением. Ламинарный режимнаблюдается преиму-щественно при движении вязких жидкостей (нефти, смазочных масел и т.п.), а также менее вязких жидкостей при их течении с небольшими скоростями.

Турбулентнымназывается течение, сопровождающееся интенсивным перемешиванием жидкости и пульсацией скоростей и давления. Движение отдельных частиц оказывается хаотичным, беспорядочным. Наряду с осевым перемещением наблюдается вращательное и поперечное перемещение отдельных объемов жидкости. Этим и объясняются пульсации скоростей и давления.

Источник

Какую скорость называют средней скоростью движения жидкости

Если отдельные частицы абсолютно твердого тела жестко связаны между собой, то в движущейся жидкой среде такие связи отсутствуют. Движение жидкости состоит из чрезвычайно сложного перемещения отдельных молекул.

если угол в радианах, или

Поскольку скорость движения различных частиц жидкости отличается друг от друга, поэтому скорость движения и усредняется. В круглой трубе, например, скорость на оси трубы максимальна, тогда как у стенок трубы она равна нулю.

Течение жидкости может быть установившимся и неустановившимся. Установившимся движением называется такое движение жидкости, при котором в данной точке русла давление и скорость не изменяются во времени

Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

Линия тока (применяется при неустановившемся движении) это кривая, в каждой точке которой вектор скорости в данный момент времени направлены по касательной.

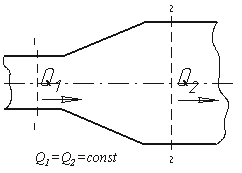
Из закона сохранения вещества и постоянства расхода вытекает уравнение неразрывности течений. Представим трубу с переменным живым сечением (рис.3.4). Расход жидкости через трубу в любом ее сечении постоянен, т.е. Q₁=Q₂= const, откуда

Таким образом, если течение в трубе является сплошным и неразрывным, то уравнение неразрывности примет вид:

Уравнение Даниила Бернулли, полученное в 1738 г., является фундаментальным уравнением гидродинамики. Оно дает связь между давлением P, средней скоростью υ и пьезометрической высотой z в различных сечениях потока и выражает закон сохранения энергии движущейся жидкости. С помощью этого уравнения решается большой круг задач.

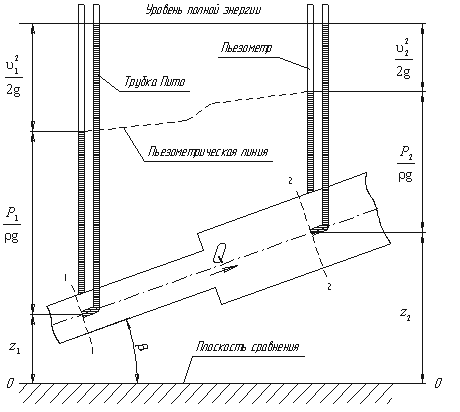
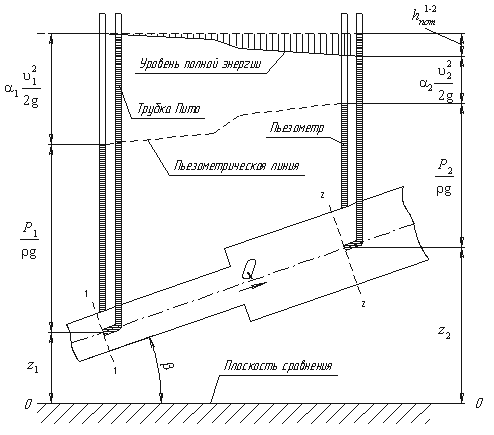
Рассмотрим трубопровод переменного диаметра, расположенный в пространстве под углом β (рис.3.5).

Выберем произвольно на рассматриваемом участке трубопровода два сечения: сечение 1-1 и сечение 2-2. Вверх по трубопроводу от первого сечения ко второму движется жидкость, расход которой равен Q.

Кроме пьезометров в каждом сечении 1-1 и 2-2 установлена трубка, загнутый конец которой направлен навстречу потоку жидкости, которая называется трубка Пито. Жидкость в трубках Пито также поднимается на разные уровни, если отсчитывать их от пьезометрической линии.

Пьезометрическую линию можно построить следующим образом. Если между сечением 1-1 и 2-2 поставить несколько таких же пьезометров и через показания уровней жидкости в них провести кривую, то мы получим ломаную линию (рис.3.5).

Однако высота уровней в трубках Пито относительно произвольной горизонтальной прямой 0-0, называемой плоскостью сравнения, будет одинакова.

Если через показания уровней жидкости в трубках Пито провести линию, то она будет горизонтальна, и будет отражать уровень полной энергии трубопровода.

Для двух произвольных сечений 1-1 и 2-2 потока идеальной жидкости уравнение Бернулли имеет следующий вид:

Так как сечения 1-1 и 2-2 взяты произвольно, то полученное уравнение можно переписать иначе:

и прочитать так: сумма трех членов уравнения Бернулли для любого сечения потока идеальной жидкости есть величина постоянная.

С энергетической точки зрения каждый член уравнения представляет собой определенные виды энергии:

Следовательно, согласно уравнению Бернулли, полная удельная энергия идеальной жидкости в любом сечении постоянна.

В этом случае уравнение Бернулли можно прочитать так: сумма геометрической, пьезометрической и скоростной высоты для идеальной жидкости есть величина постоянная.

Уравнение Бернулли для потока реальной жидкости несколько отличается от уравнения

Дело в том, что при движении реальной вязкой жидкости возникают силы трения, на преодоление которых жидкость затрачивает энергию. В результате полная удельная энергия жидкости в сечении 1-1 будет больше полной удельной энергии в сечении 2-2 на величину потерянной энергии (рис.3.6).

Потерянная энергия или потерянный напор обозначаются и имеют также линейную размерность.

Уравнение Бернулли для реальной жидкости будет иметь вид:

Из рис.3.6 видно, что по мере движения жидкости от сечения 1-1 до сечения 2-2 потерянный напор все время увеличивается (потерянный напор выделен вертикальной штриховкой). Таким образом, уровень первоначальной энергии, которой обладает жидкость в первом сечении, для второго сечения будет складываться из четырех составляющих: геометрической высоты, пьезометрической высоты, скоростной высоты и потерянного напора между сечениями 1-1 и 2-2.

Кроме этого в уравнении появились еще два коэффициента α₁ и α₂, которые называются коэффициентами Кориолиса и зависят от режима течения жидкости ( α = 2 для ламинарного режима, α = 1 для турбулентного режима ).

Потерянная высота складывается из линейных потерь, вызванных силой трения между слоями жидкости, и потерь, вызванных местными сопротивлениями (изменениями конфигурации потока)

Для измерения скорости в точках потока широко используется работающая на принципе уравнения Бернулли трубка Пито (рис.3.7), загнутый конец которой направлен навстречу потоку. Пусть требуется измерить скорость жидкости в какой-то точке потока. Поместив конец трубки в указанную точку и составив уравнение Бернулли для сечения 1-1 и сечения, проходящего на уровне жидкости в трубке Пито получим

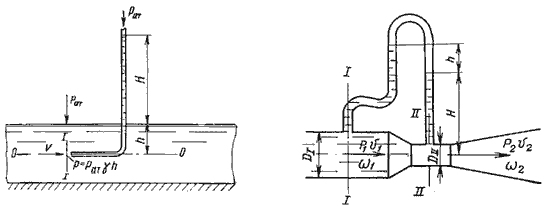
Для измерения расхода жидкости в трубопроводах часто используют расходомер Вентури, действие которого основано так же на принципе уравнения Бернулли. Расходомер Вентури состоит из двух конических насадков с цилиндрической вставкой между ними (рис.3.7). Если в сечениях I-I и II-II поставить пьезометры, то разность уровней в них будет зависеть от расхода жидкости, протекающей по трубе.

Выражение, стоящее перед 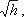, является постоянной величиной, носящей название постоянной водомера Вентури.

Из полученного уравнения видно, что h зависит от расхода Q. Часто эту зависимость строят в виде тарировочной кривой h от Q, которая имеет параболический характер.

Источник