какую силу называют уравновешивающей
Тема 1.1. Основные понятия и аксиомы статики
§1. Элементы векторной алгебры
В теоретической механике рассматриваются такие векторные величины как сила, моменты силы относительно точки и оси, момент пары сил, скорость, ускорение и другие.
1. Понятие вектора.
Операции над векторами. Вектора можно складывать и умножать на число.
— сумма двух векторов есть вектор
— существует нулевой вектор
Рис.1. Сложение векторов
В математике все вектора являются свободными, их можно переносить параллельно самим себе.
В сумме двух векторов (рис.1,а) начало второго вектора можно поместить в конец первого вектора, тогда сумму двух векторов можно представить как вектор, имеющий начало в начале первого вектора, а конец в конце второго вектора. Применяя это правило для суммы нескольких векторов (рис.1,б) получаем, что суммой нескольких векторов является вектор замыкающий ломаную линию, состоящую из слагаемых векторов.
Операции над векторами подчиняются следующим законам (см. рис.2):
Рис.2. Операции над векторами
2. Проекцией вектора на ось
Проекцией вектора на ось называется скалярная величина, которая определяется отрезком, отсекаемым перпендикулярами, опущенными из начала и конца вектора на эту ось. Проекция вектора считается положительной (+), если направление ее совпадает с положительным направлением оси, и отрицательной (-), если проекция направлена в противоположную сторону (см. рис.3).
Рис.3. Проекция вектора на ось
§2. Основные понятия статики
Статикой называется раздел механики, в котором излагается общее учение о силах и изучается условия равновесия материальных тел, находящихся под действием сил.
Твердое тело. В статике и вообще в теоретической механике все тела считаются абсолютно твердыми. То есть предполагается, что эти тела не деформируются, не изменяют свою форму и объем, какое бы действие на них не было оказано. Материальной точкой будет называться абсолютно твердое тело, размерами которого можно пренебречь.
Под равновесием будем понимать состояния покоя тела по отношению к другим материальным телам.
1. Величина, являющаяся количественной мерой механического взаимодействия материальных тел, называется в механике силой.
В Международной системе единиц (СИ) силу измеряют в ньютонах (Н), килоньютонах (кН). Сила является величиной векторной.
Ее действие на тело определяется:
1) численной величиной или модулем силы
2) направлением силы
3) точкой приложения силы (рис.4).
Рис.4. Сила, приложенная к телу
Силу, как и другие векторные величины, изображают в виде направленного отрезка со стрелкой на конце, указывающей его направление.
Прямая DE, вдоль которой направлена сила, называется линией действия силы.
Понятия «линия действия» и «направление» близки, но не тождественны. Очевидно, что по линии действия можно определить направление с точностью до противоположного. Аналогично связаны понятия «модуль» и «величина» для вектора.
2. Совокупность сил, действующих на какое-нибудь твердое тело, будем называть системой сил. Предполагается, что действие силы на тело не изменится, если ее перенести по линии действия в любую точку тела (конечно – твердого тела). Поэтому вектор силы называют скользящим вектором. Если силу перенести в точку, не расположенную на этой линии, действие ее на тело будет совсем другим.
3. Тело, не скрепленное с другими телами, которому из данного положения можно сообщить любое перемещение в пространстве, называется свободным.
4. Если одну систему сил, действующих на свободное твердое тело, можно заменить другой системой, не изменяя при этом состояния покоя или движения, в котором находится тело, то такие две системы сил называются эквивалентными.
Например, если системы сил, изображенных на рис. 5, а и рис. 5, б, уравновешены, то эти две системы сил будут эквивалентны друг другу.
Рис 5. Система сил:
а – заданная система сил; б – эквивалентная система сил
5. Система сил, под действием которой свободное твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю.
7. Сила, равная равнодействующей по модулю, прямо противоположная ей по направлению и действующая вдоль той же прямой, называется уравновешивающей силой.
8. Силы, действующие на твердое тело, можно разделить на внешние и внутренние. Внешними называются силы, действующие на частицы данного тела со стороны других материальных тел. Внутренними называются силы, с которыми частицы данного тела действуют друг на друга.
9. Сила, приложенная к телу в какой-нибудь одной его точке, называется сосредоточенной.
Силы, действующие на все точки данного объема или данной части поверхности тела, называются распределенными.
Понятие о сосредоточенной силе является условным, так как практически приложить силу к телу в одной точке нельзя. Силы, которые мы в механике рассматриваем как сосредоточенные, представляют собою по существу равнодействующие некоторых систем распределенных сил.
В частности, обычно рассматриваемая в механике сила тяжести, действующая на данное твердое тело, представляет собою равнодействующую сил тяжести его частиц. Линия действия этой равнодействующей проходит через точку, называемую центром тяжести тела.
§3. Аксиомы статики
Все теоремы и уравнения статики выводятся из нескольких исходных положений, принимаемых без математических доказательств и называемых аксиомами или принципами статики. Аксиомы статики представляют собою результат обобщений многочисленных опытов и наблюдений над равновесием и движением тел, неоднократно подтвержденных практикой. Часть из этих аксиом является следствиями основных законов механики, с которыми мы познакомимся в динамике.
Аксиома 1. Если на свободное абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю (F1 = F2) и направлены вдоль одной прямой в противоположные стороны (рис. 6).
Рис.6. Система сил, находящаяся в равновесии
Аксиома 1 определяет простейшую уравновешенную систему сил, так как опыт показывает, что свободное тело, на которое действует только одна сила, находиться в равновесии не может.
Аксиома 2. Действие данной системы, сил на абсолютно твердое тело не изменится, если к ней прибавить или от нее отнять уравновешенную систему сил.
Эта аксиома устанавливает, что две системы сил, отличающиеся на уравновешенную систему, эквивалентны друг другу.
Следствие из 1-й и 2-й аксиом. Действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела.
Рис.7. Система сил
В самом деле, пусть на твердое тело действует приложенная в точке А сила (рис.7). Возьмем на линии действия этой силы произвольную точку В и приложим к ней две уравновешенные силы
Аксиома 3 (аксиома параллелограмма сил). Две силы, приложенные к телу в одной точке, имеют равнодействующую, приложенную в той же точке и изображаемую диагональю параллелограмма, построенного на этих силах, как на сторонах.
Рис.8. Равнодействующая двух сил
Следовательно, аксиому 3 можно еще формулировать так: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке.
Аксиома 4 (принцип противодействия). При всяком действии одного материального тела на другое имеет место такое же по величине, но противоположное по направлению противодействие.
(рис. 9). Однако силы и не образуют уравновешенной системы сил, так как они приложены к разным телам. Эта аксиома соответствует третьему закону Ньютона: действие всегда равно и противоположно противодействию. При этом необходимо помнить, что в аксиоме 4 рассматривается случай, когда силы приложены к разным телам и в этом случае система сил не является уравновешенной в отличие от случая действия сил в аксиоме 2.
Рис.9. Противодействие
Рис. 10. Опирание балки на опоры:
а – схема загружения балки; б – силы действия балки на
опоры и противодействия со стороны опор на балку
Аксиома 5 (принцип отвердевания). Равновесие изменяемого (деформируемого) тела, находящегося под действием данной системы сил, не нарушится, если тело считать отвердевшим (абсолютно твердым). Из принципа отвердения следует, что условия, необходимые и достаточные для равновесия абсолютно твердого тела, необходимы, но не достаточны для равновесия деформируемого тела, по форме и размерам тождественного с данным.
Высказанное в этой аксиоме утверждение очевидно. Например, ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом и т. д.
Аксиома 6 (аксиома связей). Всякое несвободное тело можно рассматривать как свободное, если механическое действие связей заменить реакциями этих связей (пояснения к этой аксиоме в следующем параграфе).
Приведенные принципы и аксиомы положены в основу методов решения задач статики. Все они широко используются в инженерных расчетах.
Видео-урок «Аксиомы статики»
§4. Связи и их реакции
По определению, тело, которое не скреплено с другими телами и может совершать из данного положения любые перемещения в пространстве, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, будем называть связью.
Например, тело лежащее на столе – несвободное тело. Связью его является плоскость стола, которая препятствует перемещению тела вниз.
Очень важен так называемый принцип освобождаемости, которым будем пользоваться в дальнейшем. Записывается он так:
Любое несвободное тело можно сделать свободным, если связи убрать, а действие их на тело заменить силами, такими, чтобы тело оставалось в равновесии.
Сила, с которой данная связь действует на тело, препятствуя тем ила иным его перемещениям, называется силой реакции (противодействия) связи или просто реакцией связи.
Так у тела, лежащего на столе, связь – стол. Тело несвободное. Сделаем его свободным – стол уберем, а чтобы тело осталось в равновесии, заменим стол силой, направленной вверх и равной, конечно, весу тела.
Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь одновременно препятствует перемещениям тела по нескольким направлениям, направление реакции связи также наперед неизвестно и должно определяться в результате решения рассматриваемой задачи.
Если в качестве физического тела рассматривать какой-либо элемент инженерного сооружения (балка, ферма, колонна, плита и т. п.), который передает давление на опоры, то реакции опор (связей) называют опорными реакциями. Реакции связей носят вторичное происхождение, они возникают как противодействие другим силам.
Все силы, кроме реакции связей, называют заданными силами. Термин «заданные силы» имеет глубокий смысл. Заданные силы чаще всего являются активными, т.е. силами, которые могут вызвать движение тел, например: сила тяжести, снеговая или ветровые нагрузки и т.п. Учитывая сказанное выше, будем подразделять силы на активные силы и реакции связей.
Для определения направления реакции необходимо установить особенности взаимодействия твердого тела со связями различного вида. Следует иметь в виду, что реакция всегда направлена противоположно направлению возможного перемещения тела при удалении связи.
Рассмотрим, как направлены реакции некоторых основных видов связей:
1. Гладкая плоскость (поверхность) или опора. Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания (рис.11, а). Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. Когда одна из соприкасающихся поверхностей является точкой (рис. 11, б), то реакция направлена по нормали к другой поверхности.
03-в. Уравновешенные силы и равнодействующая
§ 03-в. Уравновешенные силы и равнодействующая
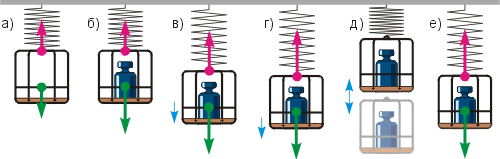
Проведём так называемый мысленный эксперимент с пружиной и подвешенной к ней корзинкой, в которую будем помещать груз.
На рисунке «а» на корзинку действуют две силы: сила тяжести со стороны Земли (зеленый вектор) и сила упругости со стороны пружины (красный вектор). Поскольку корзинка находится в покое, считаем, что эти силы уравновешивают друг друга: то есть равны по значению и противоположно направлены.
Затем в корзинку положили груз, и действующая сила тяжести увеличилась (рис. «б»). Теперь она больше, чем сила упругости, поэтому корзинка движется вниз (синяя стрелка – рис. «в»).
По мере растяжения пружины сила упругости возрастает и вскоре вновь уравновешивает силу тяжести (рис. «г»). Казалось бы, корзинка должна остановиться. Но из-за свойства инертности она не может мгновенно уменьшить скорость до нуля. Следовательно, корзинка продолжает двигаться вниз. Пружина растягивается, и сила упругости становится больше, в итоге поднимая корзинку вверх. Немного покачавшись вверх-вниз (рис. «д»), она остановится. С этого момента сила упругости пружины вновь уравновешивает силу тяжести (рис. «е»).
Итак, мы выяснили, что если на тело действуют две равные и противоположно направленные силы, то тело может покоиться, но может и двигаться прямолинейно (рис. «г»). Рассмотрим второй случай более подробно.
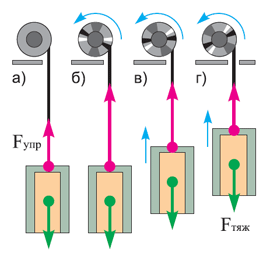
Обратимся к рисунку. На нём условно изображена кабина лифта, висящая на тросе, и двигатель, который может наматывать трос.
Сначала кабина неподвижна (рис. «а»). На неё действуют два тела: трос и Земля. Когда лифт «стоит», сила натяжения троса (F упр ) равна силе тяжести (F тяж ). Чтобы кабина поднималась, двигатель наматывает трос. Из-за свойства инертности кабина не может мгновенно прийти в движение. Поэтому трос натягивается сильнее, и сила упругости возрастает (рис. «б»). Если сила упругости всё время будет больше силы тяжести, то разгон никогда не прекратится. Однако обычно лифт разгоняется одну-две секунды, а затем движется прямолинейно и равномерно. Значит, сила упругости уменьшается и становится равной силе тяжести (рис. «г»).
Итак, мы обнаружили следующую закономерность: если на тело действуют только уравновешенные силы, то наблюдается либо покой, либо прямолинейное и равномерное движение тела. Закономерность будет верной и наоборот: если тело покоится или движется прямолинейно и равномерно, значит, на него действуют только уравновешенные силы (или не действуют совсем).
Две силы можно заменить равнодействующей силой (см. рис.).
Если силы сонаправлены, то равнодействующая сила равна их сумме и направлена в ту же сторону. Если силы противонаправлены, то равнодействующая сила равна их разности и направлена в сторону большей силы. Следствие: равнодействующая уравновешенных сил равна нулю.
Лекция 1. Основные понятия и положения статики. Сходящаяся система сил
1.1. Основные определения
Решение многих важных технических задач сводится к изучению механического движения и механического взаимодействия различных материальных тел – конструкций, машин, механизмов и их деталей и т.д. Наука о механическом движении и взаимодействии тел называется механикой.
Под механическим движением понимают изменение взаимного положения тел в пространстве с течением времени. Тело называют свободным, если его движение не стеснено другими телами. В противном случае тело называется несвободным. Механическим взаимодействием называется такое действие тел друг на друга, которое может вызвать изменение движения этих тел или их формы.
Диапазон проблем, изучаемых механикой, весьма широк. В зависимости от того, движение каких именно тел рассматривается, выделяют механику жидкости и газа, механику деформируемого твердого тела (включая теорию упругости и теорию пластичности). Наиболее общие законы механического движения и взаимодействия материальных тел изучает теоретическая механика. Как правило, в данном разделе науки рассматриваются материальные точки и абсолютно твердые тела.
Тело называют материальной точкой, если его размерами в условиях задачи можно пренебречь. Абсолютно твердое тело характеризуется тем, что расстояние между любыми двумя его точками остается постоянным. Иными словами, абсолютно твердое тело не подвержено деформации.
Разумеется, и материальная точка, и твердое тело – это идеализации. В реальности не существует тел с бесконечно малыми размерами, равно как и тел, которые нельзя деформировать. Так, поверхность стола прогибается даже под весом пушинки; дождевая капля, падающая с высоты километра, имеет небольшие, но вполне определенные размеры. Однако во многих практически важных случаях малыми деформациями, а также размерами некоторых тел можно пренебречь. Это существенно упрощает поставленные задачи, но их решения будут вполне пригодны и для описания реальных деформируемых тел конечных размеров.
На достижениях теоретической механики базируются и многие специальные технические дисциплины, например, теория механизмов и машин.
Мерой интенсивности механического взаимодействия является сила. Это векторная величина: она характеризуется своим числовым значением (модулем), направлением и точкой приложения.
Пример. Чтобы открыть дверь, к ней следует приложить некоторое усилие. В зависимости от того, куда и в каком направлении приложено это усилие, эффект будет различным. Так, если дверь толкать в точке ее подвеса, она не повернется. Аналогично, она не будет двигаться, если толкать ее в торец параллельно дверному полотну. Подробнее этот пример будет рассмотрен в Лекции 3.
В интернациональной системе единиц СИ модуль силы измеряется в ньютонах (Н). Один ньютон равен силе, с которой Земля притягивает к себе тело массой примерно 102 г, находящееся вблизи земной поверхности.
Замечание. В системе СГС («сантиметр, грамм, секунда») единицей измерения силы служит дина: 1 дин = 10 –5 Н. В технической системе единиц МКГСС («метр, килограмм-сила, секунда») сила измеряется в килограмм-силах (кГ или кгс): 1 кГ = 9.81 Н. Килограмм-сила равна силе, с которой сила тяжести действует на тело массой 1 кг. В настоящее время эта единица считается устаревшей и, по мнению Международной органиации законодательной метрологии, должна быть выведена из обращения. Тем не менее, она еще продолжает встречаться в технической литературе.
Далее векторные величины обозначаются стрелочками (\(\vec F\)), а их модули (числовые значения) – как правило, теми же буквами, но без дополнительных знаков: F. Иногда запись вида "F» будет символизировать проекцию силы на координатную ось, а для модуля силы \(\vec F\) мы будем использовать обозначение \(|\vec F|\).
Линией действия силы называется прямая, проходящая параллельно силе через ее точку приложения (рис. 1.1).
Рис. 1.1. Сила \(\vec F\) приложена к точке A. Линия действия силы показана штрихом
Вся совокупность сил, приложенных к данному телу (или системе тел), называется системой сил (рис. 1.2).
Рис. 1.2. К телу приложена система из трех сил
Система сил называется плоской, если все их линии действия лежат в одной плоскости. В противном случае систему называют пространственной.
Очевидно, прикладывая к телу разные системы сил, мы сможем оказать на него разное действие. Говорят, что системы сил эквивалентны, если они оказывают на тело одинаковое воздействие. Если заданная система эквивалентна одной силе, эту силу называют равнодействующей данной системы. Уравновешивающая сила равна равнодействующей по модулю, противоположна по направлению и действует вдоль той же прямой (рис. 1.3).
Рис. 1.3. Силы \(\vec R\) и \(\vec Q\) являются, соответственно, равнодействующей и уравновешивающей для системы \(\vec F_<1>\), \(\vec F_<2>\), \(\vec F_<3>\)
Отметим, что не у каждой системы сил есть равнодействующая (и, соответственно, уравновешивающая). Примеры систем сил, не имеющих равнодействующей, будут приведены в Лекции 3 и Лекции 6.
Силы, приложенные к телу или системе тел, можно подразделить на внешние и внутренние. Внешними называются силы, действующие со стороны тел, на принадлежащих изучаемой системе тел. Силы, действующие между телами, входящими в систему (или между частями одного тела) называются внутренними.
Пример. По отношению к наполненному воздухом воздушному шару сила земного притяжения будет внешней, а силы, с которыми молекулы горячего воздуха бьют об оболочку шара, раздувая ее, – внутренними. В то же время, если рассмотреть только оболочку шара, то силы ударов молекул будут внешними. Напротив, при рассмотрении системы «Земля + воздушный шар» сила земного притяжения оказывается внутренней.
Различают также сосредоточенные и распределенные силы. Сила называется сосредоточенной, если приложена к телу в одной конкретной точке. До сих пор в этой лекции речь шла только о сосредоточенных силах. Распределенные силы (их также называют распределенной нагрузкой) действуют на все точки, принадлежащие некоторому объему, поверхности или отрезку какой-либо линии. Сосредоточенные силы являются удобной идеализацией: действия над ними легко заменить действиями над векторами, но на практике невозможно приложить усилие к одной-единственной точке. Силу считают сосредоточенной, когда объем (площадь, длина) той области, на которой она распределена, много меньше объема всей области, рассматриваемой в задаче. Далее в пособии в большинстве случаев это ограничение считается выполненным; тот факт, что та или иная сила является распределенной, каждый раз оговаривается особо.
Пример. Силу, развиваемую при надавливании канцелярской кнопкой на стол, можно считать сосредоточенной, поскольку площадь соприкосновения заостренной части кнопки с поверхностью стола весьма мала. Опираясь на стол рукой, мы прикладываем к нему распределенное усилие, ибо ладонь соприкасается с поверхностью стола на гораздо большей площади.
Под действием некоторой системы сил тело может оказаться в равновесии, т.е. не изменять своего положения относительно других тел (например, относительно Земли) или двигаться относительно них прямолинейно и равномерно. В таком случае систему сил, приложенных к телу, называют уравновешенной (экивалентной нулю).
Замечание. Как видно, понятие равновесия является более общим, чем понятие покоя. Действительно, состояние покоя можно рассматривать как движение с постоянной нулевой скоростью. По определению, механическое взаимодействие, выражаемое силой, может привести к изменению движения (а не положения непосредственно). Если тело движется прямолинейно и равномерно (в частности, покоится), такого изменения не происходит, а значит, воздействия на данное тело со стороны других тел уравновешены.
Раздел механики, излагающий общее учение о силах и изучающий равновесие тел, называется статикой. В статике решаются две основные задачи:
Знание статики очень важно для инженера-строителя: проектируемые здания и сооружения должны выдерживать большие нагрузки и занимать устойчивое неподвижное положение.
Рис. 1.4. Александровская колонна
Другими разделами теоретической механики являются кинематика и динамика. Первый из них изучает движение тел без учета действующих на них сил, а второй – движение тел под действием сил.
1.2. Исходные положения статики
Как и теоретическая механика в целом, статика основывается на небольшом количестве исходных положений (аксиом), из которых с помощью логических рассуждений и математических выкладок выводятся другие утверждения, формулы и т.д. Ниже перечисляются аксиомы статики:
Аксиома 1. Система из двух сил, приложенных к одному и тому же абсолютно твердому телу, уравновешена тогда и только тогда, когда они равны по модулю, противоположны по направлению и имеют общую линию действия (рис. 1.5).
Рис. 1.5. Равновесие твердого тела под действием двух сил
Пример. Если два человека с равными силами тянут тележку в противоположные стороны (рис. 1.6 а) или толкают ее каждый от себя (рис. 1.6 б), она не сдвинется с места.
Требование к двум уравновешенным силам – иметь общую линию действия – весьма существенно: если оно нарушается, образуется пара сил, которая не является уравновешенной системой.
Замечание. Теперь можно объяснить происхождение термина «уравновешивающая», введенного в п. 1.1. Действительно, согласно данному ранее определению и аксиоме 1, уравновешивающая и равнодействующая образуют систему сил, эквивалентную нулю. Поэтому исходная система сил (без равнодействующей) с присоединенной к ней уравновешивающей также будет уравновешенной.
Важно указать и на такой факт: под действием одной силы свободное тело будет находиться в равновесии тогда и только тогда, когда эта сила равна нулю.
Замечание. Последнее утверждение более подробно обсуждается не в статике, а в динамике.
Аксиома 2. Действие заданной системы сил на абсолютно твердое тело не изменится, если к этой системе добавить или из нее исключить уравновешенную систему сил.
Эту аксиому можно сравнить с известным свойством чисел: если к любому числу прибавить или вычесть из него нуль, исходное число не изменится.
Следствие. Действие силы на твердое тело не меняется при переносе ее точки приложения вдоль линии действия. Иными словами, силу можно считать приложенной в любой точке ее линии действия – вектор силы является скользящим.
(Отметим, что вектор называют скользящим, если его можно откладывать от любой точки на его линии действия, не меняя при этом действия самого вектора. Если же вектор может быть отложен от любой точки пространства без изменения действия, то его называют свободным. Векторы, изученные в школьном курсе элементарной математики, – свободные. Сила же таким вектором не является. Более подробно вопрос об откладывании одной и той же силы от разных точек будет разобран далее.)
Доказательство. Предположим, что сила \(\vec F\) отложена от точки A, и требуется перенести ее в некоторую точку B на той же линии действия, как показано на рис. 1.7 а). Для этого присоединим к исходной силе уравновешенную систему сил \(\vec F’\), \(\vec F»\), направленных вдоль той же линии действия, что и \(\vec F\). Очевидно, одна из них (пусть \(\vec F’\)) окажется сонаправленной с \(\vec F\), а другая (\(\vec F»\)) – направленной противоположно ей. Дополнительно потребуем, чтобы сила \(\vec F’\) была отложена от точки B (рис. 1.7 б). Мы имеем на это право, поскольку в аксиоме 1 ничего не сказано о выборе точек приложения уравновешенных сил на их общей линии действия.
После таких построений силы \(\vec F\) и \(\vec F»\) равны по модулю, противоположны по направлению и разделяют общую линию действия. Значит, они уравновешивают друг друга, и их можно отбросить; в итоге остается лишь сила \(\vec F’\). Если теперь сравнить начало и конец рассуждений, то вместо силы, отложенной от точки A мы получили равную по величине и сонаправленную ей силу, отложенную от заданной точки B на той же линии, т.е. добились желаемого результата.
Пример. Чтобы передвинуть одну и ту же тележку с грузом, ее можно либо тянуть, либо толкать (рис. 1.8). Если в обоих случаях прикладывать к ней одну и ту же по величине силу вдоль одной и той же линии действия, то эффект будет одинаковым.
Аксиома 3 (правило параллелограмма сил). Две силы, приложенные к одному и тому же телу в одной и той же точке, имеют равнодействующую, отложенную от этой же точки. Эта равнодействующая изображается диагональю параллелограмма, построенного на исходных силах, как на сторонах (рис. 1.9).
Другими словами, силы, отложенные от одной точки, можно складывать, пользуясь известными правилами действий над векторами.
Рис. 1.9. \(\vec R\) – равнодействующая сил \(\vec F_<1>\) и \(\vec F_<2>\)
Замечание 1. С точки зрения математики безразлично, каким правилом – параллелограмма или треугольника – пользоваться при сложении векторов. Тот же самый вектор \(\vec F_<2>\) на рис. 1.9 можно отложить от конца вектора \(\vec F_<1>\), сложив две силы по правилу треугольника.
Замечание 2. Если к телу приложены две взаимно уравновешенные силы, то их (пользуясь тем, что сила – скользящий вектор) можно отложить от одной точки (рис. 1.10). Если теперь сложить их по правилу параллелограмма, то получится нулевой вектор, ибо параллелограмм сил вырождается в отрезок.
Отметим, что складывать силы, приложенные к разным телам, нельзя: непонятно, к какому телу приложена их равнодействующая.
Аксиома 4 (закон равенства действия и противодействия). Любые два взаимодействующих тела действуют друг на друга с силами, равными по величине, но противоположными по направлению.
Аналогично предыдущей аксиоме, нельзя сказать, что две эти силы образуют уравновешенную систему, ибо они приложены к разным телам.
Аксиома 5 (свойство внутренних сил). При исследовании равновесия твердого тела следует учитывать только внешние силы. Внутренние силы образуют уравновешенную систему и потому при рассмотрении равновесия тела в целом не берутся в расчет.
Замечание. Можно попытаться рассмотреть это утверждение не как самостоятельную аксиому, а как следствие предыдущего исходного положения статики. Действительно, разделим исходное твердое тело на две части. По аксиоме 4, силы, с которыми они взаимодействуют, равны по модулю и противоположны по направлению. С другой стороны, эти силы можно считать приложенными к телу в целом и сделать вывод, что в этом случае они уравновешивают друг друга. Однако возникает вопрос: где гарантия, что у этих сил общая линия действия? Этот факт в общем случае не так просто обосновать, поэтому будем считать свойство внутренних сил самостоятельной аксиомой.
Аксиома 6 (принцип отвердевания). Если деформируемое тело под действием приложенных сил находится в равновесии, то абсолютно твердое тело той же формы и размеров также находится в равновесии.
Пример. Пусть две равные по силе команды перетягивают канат (рис. 1.11). С точки зрения теоретической механики, ничего не изменится, если заменить его жестким стержнем той же формы, размеров и массы.
Обратное, вообще говоря, неверно. Может оказаться так, что абсолютно твердое тело уравновешено, а деформируемое (тех же размеров и формы) – нет. Так, жесткий стержень из предыдущего примера останется в равновесии и в случае, когда его будут не растягивать, а сжимать, прикладывая к противоположным концам равные силы. Канат же в этом случае сомнется.
1.3. Сходящаяся система сил
Рассмотрим систему сил \(\vec F_<1>\), \(\vec F_<2>\), \(\vec F_<3>\). приложенных к твердому телу, и попытаемся найти их равнодействующую. Это просто, если все силы отложены от одной точки. Сначала по правилу параллелограмма сложим \(\vec F_<1>\) и \(\vec F_<2>\), заменив их одной равнодействующей \(\vec R_<1>\); затем таким же образом сложим силы \(\vec R_<1>\) и \(\vec F_<3>\), заменяя их силой \(\vec R_<2>\), и т.д. (рис. 1.12).
Рис. 1.12. Последовательное сложение нескольких сил по правилу параллелограмма
Тем самым, на каждом следующем шаге мы будем переходить к эквивалентной системе сил, содержащей на одну силу меньше, чем на предыдущем шаге. В конце концов, останется единственная сила, приложенная к телу; она и будет равнодействующей исходной системы.
Возникает вопрос: как быть, если точки приложения сил не совпадают?
Дадим определение. Система сил, приложенных к телу, называется сходящейся, если все их линии действия пересекаются в одной точке (рис. 1.13).
Рис. 1.13. Сходящаяся система сил
В таком случае можно воспользоваться следствием из аксиомы 2 и перенести все силы в точку пересечения их линий действия, после чего сложить, как описано выше. Отсюда можно сделать важный вывод:
Сходящаяся система сил имеет равнодействующую. Она представляет собой векторную сумму сил, приложенных к телу, и прикладывается в точке пересечения их линий действия.
Замечание. Если твердое тело находится под действием сходящейся системы сил, то его во многих случаях можно считать материальной точкой. Размеры тела перестают играть роль – оно «стягивается» в ту точку, где пересекаются линии действия всех приложенных к нему сил.
Как уже было сказано, при сложении сил, отложенных от одной точки, применяются обычные «школьные» правила действий над векторами. Например, их можно складывать по правилу многоугольника: начало каждого следующего вектора силы должно совпадать с концом предыдущего. При этом самый первый вектор откладывается от точки пересечения A линий действия сил. Полученная геометрическая фигура называется силовым многоугольником. Чтобы найти равнодействующую \(\vec R\), остается соединить начало многоугольника с его концом (рис. 1.14).
Рис. 1.14. Построение силового многоугольника и равнодействующей
Если известны компоненты сил вдоль осей некоторой системы координат, все операции можно произвести аналитически, складывая или вычитая соответствующие проекции разных сил.
Замечание. Далее при действиях над векторами в кординатах будем всегда предполагать, что используемая система координат – декартова прямоугольная. Если речь идет о координатах в пространстве, то система координат считается правой: при взгляде с конца третьей оси кратчайший поворот от первой оси ко второй должен быть виден происходящим проив часовой стрелки. Все эти свойства далее специально оговариваться не будут.
Выше отмечалось, что одной из основных задач статики служит изучение условий равновесия систем сил, действующих на твердые тела. Для изучаемого нами случая это условие формулируется так:
Тело под действием сходящейся системы сил находится в равновесии, если геометрическая сумма всех приложенных к нему сил равна нулю.
Действительно, сходящаяся система эквивалентна одной силе – равнодействующей. Следовательно, если система уравновешена, то эта сила должна быть нулевой. Поэтому силовой многоугольник уравновешенной системы должен быть замкнутым – для получения нулевой равнодействующей его начало обязано совпасть с концом.
Очевидно, плоская система из двух непараллельных сил всегда является сходящейся: на плоскости прямые либо пересекаются, либо параллельны. Три силы уже могут не быть сходящимися: линия действия третьей силы может «проехать» мимо точки пересечения первых двух. Связать вопросы о равновесии и сходимости плоской системы трех непараллельных сил помогает следующее утверждение.
Теорема (о трех силах). Если твердое тело под действием плоской системы из трех сил находится в равновесии, то их линии действия пересекаются в одной точке.
Доказательство. Пусть к телу приложены силы \(\vec F_<1>\), \(\vec F_<2>\), \(\vec F_<3>\), лежащие в одной плоскости, причем \(\vec F_<1>\) и \(\vec F_<2>\) не параллельны. Тогда их линии действия пересекаются, и эти силы имеют равнодействующую \(\vec R\) (рис. 1.15).
Рис. 1.15. Доказательство теоремы о трех силах
Исходная уравновешенная система \(\vec F_<1>\), \(\vec F_<2>\), \(\vec F_<3>\) эквивалентна двум силам \(\vec F_<3>\) и \(\vec R\), которые, таким образом, обязаны уравновешивать друг друга. Значит, они разделяют общую линию действия. Но (по нашему построению) на ней лежит точка пересечения линий действия сил \(\vec F_<1>\) и \(\vec F_<2>\). Тем самым, линии действия всех трех исходных сил пресекаются в этой точке. Теорема доказана.
Обратное неверно: понятно, что произвольная сходящаяся плоская система трех сил не обязана быть уравновешенной. Она может иметь равнодействующую, не равную нулю.
В пространстве уже и система из двух непараллельных сил может не быть сходящейся, ибо их линии действия в пространстве могут оказаться скрещивающимися.
Вопросы для самоконтроля
Задачи к лекции
Силы \(F_<1>=6\sqrt<2>\) Н и F2 = 2 Н приложены к одной точке и образуют угол 45°. Найти величину их равнодействующей.
Указание. Воспользуйтесь теоремой косинусов.
Силы \(\vec F_<1>\), \(\vec F_<2>\) и \(\vec F_<3>\) лежат в плоскости Oxy, причем их линии действия проходят через начало координат. Сила \(\vec F_<1>\), численно равная 20 Н, образует с положительным направлением оси Ox угол, равный 30°, сила \(\vec F_<2>\), численно равная \(20\sqrt<3>\) Н, – угол в 120°, а сила \(\vec F_<3>\), чья величина составляет 10 Н, – угол 270°. Найти величину их уравновешивающей и угол, который она образует с положительным направлением оси абсцисс.
Указание. Запишите уравнения линий действия всех сил, найдите точку пересечения первых двух линий и докажите, что третья линия проходит через эту точку.
Ответы. 1. 10 Н. 2. 30 Н; 90°. 3. 300 Н. 4. \(\vec R=\<-1;7\>\); A(1; 2).