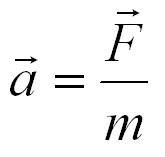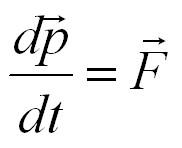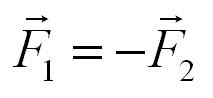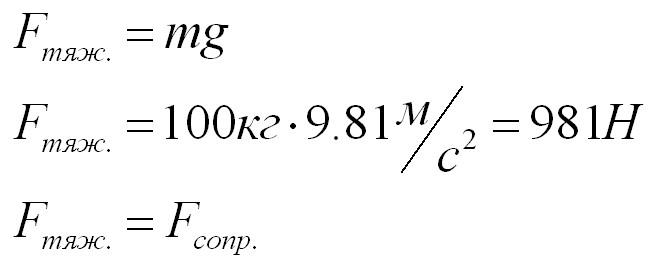какую силу может приложить человек в ньютонах
Об экспертной оценке силы ударов тупыми твердыми предметами
библиографическое описание:
Об экспертной оценке силы ударов тупыми твердыми предметами / Капустин А.В. // Судебно-медицинская экспертиза. — М., 1999. — №1. — С. 18-20.
код для вставки на форум:
Обычно эксперты оценивают силу удара очень приблизительно как «большую» или «небольшую». Указанный вывод эксперта иногда вызывает возражения юристов (следователя, адвоката, членов суда) полагающих, что такая формулировка выводов не является научно обоснованной и носит житейский, бытовой характер.
Следует признать, что указанная оценка силы удара является не только приблизительной, но и весьма субъективной, что снижает ее доказательное значение.
Анализ работ судебных медиков, изучавших различные аспекты механизма и условия возникновения повреждений при действии тупым предметов, позволяют выделить четыре степени силы удара тупыми предметами:
Такая градация произведена с учетом данных о силе ударов, вызывающих различные повреждения. Наиболее подробно среди различных повреждений изучены условия возникновения переломов костей черепа и некоторых других костей скелета. Значительно хуже, а то и вообще не изученными в этом отношении являются повреждения внутренних органов, что затрудняет оценку силы ударов, причинивших их повреждения.
Сила удара не является единственным фактором, определяющим возникновение и величину повреждений. Многие авторы убедительно показали, что, например, повреждения костей черепа определяются не только силой удара, но и формой черепа, толщиной его костей, направлением удара, размерами ударяющей поверхности тупого предмета, временем (быстротой) удара и рядом других факторов. В этой связи взятый отдельно от всех других факторов показатель силы удара неизбежно приобретает только ориентировочное значение.
Повреждения, которые соответствуют различными показателями силы удара тупыми предметами:
О значительной силе удара свидетельствует образование размозжение подкожной жировой клетчатки и отслоение кожи, что происходит при силе удара более 196 Н.
При еще большей силе удара (более 313 Н) образуются повреждения внеорганных магистральных сосудов.
Среди повреждений, возникающих при ударах большой силы, следует назвать вдавленные переломы, образующие при ударе по голове с силой от 1960 до 4901 Н предметом с ограниченной ударяющей поверхностью.
По данным С.Л. Корсакова, переломы костей свода черепа в виде трещины внутренней костной пластинки (начало образования перелома) возникают при ударах с силой от 2186 до 2657 Н. При ударах головой о тупой широкий предмет начало появления трещин отмечается при ударах с силой свыше 3121,5 Н.
Сила удара, необходимая для возникновения переломов костей основания черепа, установлена рядом авторов. Так, единичные трещины в передней черепной ямке при ударах лобно-теменной областью головы о широкий тупой предмет возникают при силе удара 3922 Н. Появление единичных трещин в задней черепной ямке при тех же условиях травмы отмечается при силе удара 4217 Н.
Средняя величина силы, необходимой для более значительных переломов костей передней черепной ямки, составляет 4805,4 Н.
Дальнейшее увеличение повреждений основания черепа происходит при нанесении ударов с очень большой силой. Например, при ударах лобно-теменной областью головы о широкий предмет с силой от 5511 до 6962,9 Н переломы (трещины) возникающие в передней черепной ямке, распространяются в среднюю черепную ямку. При силе ударов от 7257,1 до 10689,6 Н наряду с трещинами костей свода черепа возникают переломы костей основания не только передней и средней, но и задней черепной ямки.
Можно также отметить, что при ударах по голове предметом с небольшой ударяющей поверхностью с силой 5884,2 Н возникают дырчатые переломы без дополнительных трещин.
Переломы нескольких ребер и грудины возникают при ударах, нанесенных с большой или очень большой силой. По данным Г.С. Бачу и соавт. При нанесении из положения стоя и ударе передней поверхностью грудной клетки о деревянный брусок шириной 6 см в экспериментах на трупах в зависимости от места удара и его силы образуются следующие переломы:
Приведенные данные не касаются повреждений внутренних органов. Тем не менее, некоторое представление о силе ударов, приводящих к повреждениям этих органов, они могут дать. Например, при ушибах головного мозга без повреждения кости свода черепа и основания черепа сила удара, причинившего ушиб мозга, должна быть меньше минимальной силы, необходимой для возникновения переломов. При этом нужно учитывать механизм травмы (удар по голове или головой о тупой предмет), место приложения силы, размер ударяющей поверхности тупого предмета и т.д. В зависимости от этих условий, а также в зависимости от особенностей повреждений головного мозга (у живых людей – и от тяжести ушиба) сила удара при отсутствии повреждений костей свода и основания черепа может быть значительной или большой.
Следует учитывать, что сила удара кулаком мужчины, даже не занимающегося физической работой, может быть более 5000 – 6000 Н, в связи с чем при ударе кулаком могут возникать повреждения оболочек и вещества головного мозга, причем при ударах в область лица и быстром наступлении смерти потерпевшего повреждения мягких тканей лица могут и не возникнуть (особенно при ударах в область подбородка). При этом могут возникнуть лишь небольшие кровоподтеки, поверхностные небольшие ушибленные раны или ссадины.
Вопрос о силе удара, приводящего к повреждению крупных органов грудной и брюшной полостей, требует дальнейшего изучения. Однако, учитывая закрытость этих органов, их топографию и особенности повреждений (от кровоизлияний до разрывов размозжений), следует по- видимому, оценивать силу ударов, необходимую для их повреждений, в зависимости от обширности этих повреждений, по меньшей мере как значительную или большую. Очевидно, что при очень больших грубых повреждениях речь может идти только об очень большой силе удара.
Приведенные данные, несмотря на их неполноту и отсутствие конкретных показателей силы, при которой образуются повреждения внутренних органов, позволяют оценить предлагаемую схему силы ударов тупым предметом как вполне приемлемую и убедительную. Эта схема позволяет судебно-медицинскую эксперту не только давать приблизительную словесную оценку силы удара тупым предметом, причинившим повреждение, но и подкрепить эту оценку количественными показателями ее величины в ньютонах. Это придаст выводу эксперта достоверность и убедительность, причем определение величины силы в интервалах ее показателей не умаляет вывода эксперта, но делает его научно обоснованным и объективным.
Научный форум dxdy
Математика, Физика, Computer Science, Machine Learning, LaTeX, Механика и Техника, Химия,
Биология и Медицина, Экономика и Финансовая Математика, Гуманитарные науки
Мышечная сила человека
 |
Хотела написать в физику, но решила, что забанят.
Как известно каждому школьнику, сила равна массе, умноженной на ускорение.
Пауэрлифтеры, к примеру, поднимают исполинские веса, но поднимают их крайне медленно (кто занимался сам или видел по телеку (как я), тот поймёт).
Тяжелоотлеты (я имею в виду олимпийскую тяжёлую атлетику (рывок и толчок)) напротив, поднимают меньше (абсолютный рекорд в рывке = 216 кг), но с огромным ускорением. Где-то прочла, что сила штангиста может доходить до 8000 ньютонов.
У каратистов и кикбоксёров сила удара может достигать тонны (я имею в виду тонна-силу, равную 10 тыс. ньютонов (если принимать ускорение свободного падения равным 10)). Во всяком случае, так по National Geographic передавали.
Интересно также рассмотреть и спринтеров, какую силу развивают они.
Короче, мой вопрос звучит по-детски:
Как узнать, кто самый сильный? Представители какого из видов спорта развивают наибоьшую мышечную силу (в ньютонах)?
|
|
Стало быть, сравнивать можно и, я бы сказала, нужно!
|
Вопрос в том, в течение какого времени атлет может эту силу выдавать на гора.
|
Вопрос в том, в течение какого времени атлет может эту силу выдавать на гора.
| Заслуженный участник |
 |
|
| Заслуженный участник |
|
Последний раз редактировалось caxap 12.05.2011, 16:54, всего редактировалось 1 раз.
|
| Заслуженный участник |
|
|
|
Последний раз редактировалось Xenia1996 12.05.2011, 20:14, всего редактировалось 1 раз.
| Заслуженный участник |
|
| Заблокирован |
 |
Кто сейчас на конференции
Сейчас этот форум просматривают: нет зарегистрированных пользователей
Законы Ньютона для «чайников»: объяснение 1, 2, 3 закона, пример с формулами
Мы уже говорили об основах классической механики. Настала пора поговорить о них подробнее и затронуть в обсуждении чуть больше, чем просто основу. В этой статье мы подробно разберем основные законы классической механики. Как вы уже догадались, речь пойдет о законах Ньютона.
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Основные законы классической механики Исаак Ньютон (1642-1727) собрал и опубликовал в 1687 году. Три знаменитых закона были включены в труд, который назывался «Математические начала натуральной философии».
Был долго этот мир глубокой тьмой окутан
Да будет свет, и тут явился Ньютон.
(Эпиграмма 18-го века)
(Эпиграмма 20-го века)
Что стало, когда пришел Эйнштейн, читайте в отдельном материале про релятивистскую динамику. А мы пока приведем формулировки и примеры решения задач на каждый закон Ньютона.
Первый закон Ньютона
Первый закон Ньютона гласит:
Существуют такие системы отсчета, называемые инерциальными, в которых тела движутся равномерно и прямолинейно, если на них не действуют никакие силы или действие других сил скомпенсировано.
Проще говоря, суть первого закона Ньютона можно сформулировать так: если мы на абсолютно ровной дороге толкнем тележку и представим, что можно пренебречь силами трения колес и сопротивления воздуха, то она будет катиться с одинаковой скоростью бесконечно долго.
Инерция – это способность тела сохранять скорость как по направлению, так и по величине, при отсутствии воздействий на тело. Первый закон Ньютона еще называют законом инерции.
До Ньютона закон инерции был сформулирован в менее четкой форме Галилео Галилеем. Инерцию ученый называл «неистребимо запечатленным движением». Закон инерции Галилея гласит: при отсутствии внешних сил тело либо покоится, либо движется равномерно. Огромная заслуга Ньютона в том, что он сумел объединить принцип относительности Галилея, собственные труды и работы других ученых в своих «Математических началах натуральной философии».
Понятно, что таких систем, где тележку толкнули, а она покатилась без действия внешних сил, на самом деле не бывает. На тела всегда действуют силы, причем скомпенсировать действие этих сил полностью практически невозможно.
Например, все на Земле находится в постоянном поле силы тяжести. Когда мы передвигаемся (не важно, ходим пешком, ездим на машине или велосипеде), нам нужно преодолевать множество сил: силу трения качения и силу трения скольжения, силу тяжести, силу Кориолиса.
Второй закон Ньютона
Помните пример про тележку? В этот момент мы приложили к ней силу! Интуитивно понятно, что тележка покатится и вскоре остановится. Это значит, ее скорость изменится.
В реальном мире скорость тела чаще всего изменяется, а не остается постоянной. Другими словами, тело движется с ускорением. Если скорость нарастает или убывает равномерно, то говорят, что движение равноускоренное.
Если рояль падает с крыши дома вниз, то он движется равноускоренно под действием постоянного ускорения свободного падения g. Причем любой дугой предмет, выброшенный из окна на нашей планете, будет двигаться с тем же ускорением свободного падения.
Второй закон Ньютона устанавливает связь между массой, ускорением и силой, действующей на тело. Приведем формулировку второго закона Ньютона:
Ускорение тела (материальной точки) в инерциальной системе отсчета прямо пропорционально приложенной к нему силе и обратно пропорционально массе.
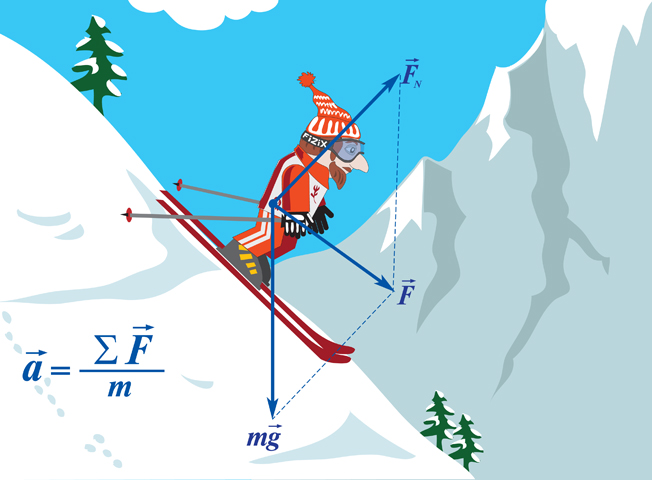
Если на тело действует сразу несколько сил, то в данную формулу подставляется равнодействующая всех сил, то есть их векторная сумма.
Существует более универсальная формулировка данного закона, так называемый дифференциальный вид.
В любой бесконечно малый промежуток времени dt сила, действующая на тело, равна производной импульса тела по времени.
Третий закон Ньютона
В чем состоит третий закон Ньютона? Этот закон описывает взаимодействие тел.
3 закон Ньютона говорит нам о том, что на любое действие найдется противодействие. Причем, в прямом смысле:
Два тела воздействуют друг на друга с силами, противоположными по направлению, но равными по модулю.
Формула, выражающая третий закон Ньютона:
Пример задачи на законы Ньютона
Вот типичная задачка на применение законов Ньютона. В ее решении используются первый и второй законы Ньютона.
Десантник раскрыл парашют и опускается вниз с постоянной скоростью. Какова сила сопротивления воздуха? Масса десантника – 100 килограмм.
Решение:
Движение парашютиста – равномерное и прямолинейное, поэтому, по первому закону Ньютона, действие сил на него скомпенсировано.
На десантника действуют сила тяжести и сила сопротивления воздуха. Силы направлены в противоположные стороны.
По второму закону Ньютона, сила тяжести равна ускорению свободного падения, умноженному на массу десантника.
Ответ: Сила сопротивления воздуха равна силе тяжести по модулю и противоположна направлена.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
А вот еще одна физическая задачка на понимание действия третьего закона Ньютона.
Комар ударяется о лобовое стекло автомобиля. Сравните силы, действующие на автомобиль и комара.
Решение:
По третьему закону Ньютона, силы, с которыми тела действуют друг на друга, равны по модулю и противоположны по направлению. Сила, с которой комар действует на автомобиль, равна силе, с которой автомобиль действует на комара.
Другое дело, что действие этих сил на тела сильно отличаются вследствие различия масс и ускорений.
Исаак Ньютон: мифы и факты из жизни
На момент публикации своего основного труда Ньютону было 45 лет. За свою долгую жизнь ученый внес огромный вклад в науку, заложив фундамент современной физики и определив ее развитие на годы вперед.
Он занимался не только механикой, но и оптикой, химией и другими науками, неплохо рисовал и писал стихи. Неудивительно, что личность Ньютона окружена множеством легенд.
Ниже приведены некоторые факты и мифы из жизни И. Ньютона. Сразу уточним, что миф – это не достоверная информация. Однако мы допускаем, что мифы и легенды не появляются сами по себе и что-то из перечисленного вполне может оказаться правдой.
В самом конце предлагаем посмотреть видеоурок на тему «Законы Ньютона».
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Сила. Три закона Ньютона
Понятие силы в механике — это ключевое понятие. Ключевое — значит основное. Как чупа-чупс без палочки станет обычной никому не интересной карамелькой, так и механика (а точнее — динамика) без силы будет набором непонятной абракадабры.
Из жизни мы знаем, что тела могут действовать друг на друга: мальчик толкает тележку, Солнце притягивает Землю, магнит притягивает железные предметы и т.д.
Сила — это физическая величина, которая как раз таки и характеризует взаимодействие между телами. Сила показывает:
Но на одно и то же тело может действовать несколько тел сразу. Например, тот же железный болт может одновременно притягиваться двумя магнитами:
Логика и наш жизненный опыт подсказывают нам, что притягивать будут оба магнита одновременно. И болт будет притягиваться некоторой «средней силой» так, как будто вместо этих двух магнитов действует один магнит, расположенный примерно посередине между двумя настоящими магнитами.
Все верно. Именно так и будет. А результирующая сила (мы для понятности назвали ее «средняя сила») — это сумма двух сил:
Напомним вам, что силы — это векторы. А векторы складываются двумя способами:
В нашем примере мы сложили силы по правилу параллелограмма. Если вам непонятен способ сложения векторов, рекомендуем посмотреть тему » Два вида физических величин: скалярные величины и векторные величины «.
На тело, находящееся на горизонтальной плоскости, действуют две горизонтальные силы (см. рисунок, вид сверху).
Три закона Ньютона
Три закона Ньютона определяют «правила жизни» в механике. Обычно в школе их излагают в прямой последовательности — от первого закона к третьему. Мы поступим по-другому. Мы изложим их в обратном порядке. Нам кажется, что так будет понятнее. Приступим.
Можно предположить, что когда тело А воздействует на другое тело — тело B (например, вы действуете на стол), — то и тело B действует на тело А.
Рассмотрим другой пример. Девочка А и девочка B стоят на коньках на льду. Девочка А начинает толкать девочку B. Наш жизненный опыт подсказывает нам, что девочка B будет двигаться в ту сторону, куда ее толкает девочка А. Но! Жизненный опыт нам подсказывает, что и девочка А начнет двигаться так, будто ее толкнула девочка B.
Это подтверждает нашу догадку, что когда тело А действует с некоторой силой на тело B, то и тело B действует на тело А.
Оказывается, что наше предположение — верное. Более того, силы, с которыми тела действуют друг на друга, одинаковые (!).
Итак, третий закон Ньютона звучит следующим образом:
Итак, можно сделать вывод, что сила придает телу ускорение, она «создает» ускорение тела. Логично будет предположить, что бОльшая сила даст мячику бОльшее ускорение: ускорение тела тем больше, чем больше сила. Но это еще не все.
Возьмем два мячика: легкий шарик для пинг-понга и тяжелый железный шарик из подшипника. Подействуем на них одинаковой силой. Оба они получат ускорение. Но ускорение будет разное. Это подсказывает нам жизненный опыт.
Более тяжелый (массивный, с большей массой ) стальной шарик получит небольшую скорость; его ускорение будет небольшим.
Легкий (с меньшей массой ) шарик для пинг-понга получит большую скорость; ускорение у него будет большим.
Как правильно записать связь ускорения, массы и силы?
Итак, мы готовы к тому, чтобы записать второй закон Ньютона. Он звучит так:
Куда в этот момент направлен вектор действующей на точку силы?
А первый закон Ньютона говорит о том, где (при каких условиях) работают 3-й и 2-й законы Ньютона. Оказывается, 2-й и 3-й законы Ньютона работают только в инерциальных системах отсчета.
Инерциальные системы отсчета — это системы отсчета, в которых тела двигаются равномерно, прямолинейно и поступательно (или же находятся в состоянии покоя), если на тела не действуют никакие другие тела или действие этих тел скомпенсировано.
«Ух, как сложно», — можете сказать вы. «Да, вы правы», — ответим мы вам. Если говорить по-простому, то инерциальные системы — это системы, в которых тела, на которые не действуют силы (или их суммарное действие равно нулю), будут либо стоять на месте, либо двигаться с постоянной скоростью в неизменном направлении. В таких системах любое изменение скорости (то есть наличие ускорения) связано только с действием силы. Скорость не может меняться, если нет силы.
А вот в НЕинерциальных системах скорость тела может меняться без силы. То есть может меняться беспричинно.
Пример: представьте, что вы стоите в центре автобуса с полностью затонированными стеклами. И этот «пацанский» автобус равномерно едет по идеально ровной дороге. Находясь внутри, вы даже не чувствуете, что автобус едет.
В какой-то момент автобус резко тормозит. Что будет происходить с вами? Жизненный опыт подсказывает нам, что что вы резко «полетите» вперед. При этом на вас не действует никакая сила. То есть вы начинаете двигаться относительно автобуса без всякой причины. Автобус — это пример неинерциальной системы отсчета. Неинерциальные системы отсчета — это системы, которые двигаются с ускорением. В них не работают законы Ньютона. Тела в таких системах отсчета могут беспричинно менять свою скорость. С такими системами мы работать не будем.
Нашу Землю можно условно отнести к инерциальным системам отсчета. Почему? Земля на самом деле неинерциальна. Неинерциальна она потому, что Земля вращается. А это значит, что Земля двигается с центростремительным ускорением. А такие системы (двигающиеся с ускорением) являются неинерциальными. Но так как Земля вращается достаточно медленно, то и центростремительное ускорение получается небольшим. Поэтому условно Землю можно считать инерциальной системой отсчета.