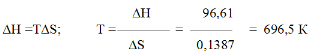какую размерность имеет энтальпия
Что такое энтальпия? (и его 11 видов)
Содержание:
И из всех физических величин, с которыми справляется эта дисциплина, одним из самых важных, несомненно, является энтальпия. Изменение этого термодинамического свойства определяет, что химические реакции в системе являются экзотермическими (они выделяют тепло) или эндотермическими (они поглощают тепло), что очень важно во многих областях науки.
Но что такое энтальпия? Как рассчитывается? Какие бывают типы? Как это связано с энтропией? В сегодняшней статье мы ответим на эти и многие другие вопросы об этой энергии, которая, хотя мы ее и не видим, определяет природу всего, что нас окружает.
Что такое энтальпия?
Энтальпия, представленная как H, это количество энергии, которым термодинамическая система в условиях постоянного давления обменивается с окружающей средой.. Другими словами, это термодинамическое свойство, изменение которого определяет, выделяет ли рассматриваемая химическая реакция энергию в виде тепла или необходимо поглощать эту тепловую энергию.
Следовательно, энтальпию можно понимать как количество тепловой энергии, которую термодинамическая система (регулируемая потоками температуры и энергии) излучает или поглощает, когда она находится под постоянным давлением. А под термодинамической системой мы можем понимать, в основном, любой физический объект.
Это одно из самых фундаментальных термохимических свойств, поскольку мы анализируем, как реакционная среда обменивается теплом (поглощая или выделяя его) с окружающей средой. А поглотит он его или высвободит, будет определяться не самой энтальпией (H), а ее изменением (ΔH).. И исходя из этого химическая реакция может быть двух типов:
Экзотермический: Когда ΔH 0 (изменение энтальпии отрицательное), реакция выделяет энергию в виде тепла. Они не потребляют тепло, а излучают его. Все реакции, в которых конечный продукт молекулярно проще, чем исходный, будут экзотермическими.
Эндотермический: Когда ΔH> 0 (изменение энтальпии положительное), реакция потребляет энергию в виде тепла. Они не выделяют энергию, а должны ее поглощать и расходовать. Все реакции, в которых конечный продукт молекулярно более сложен, чем исходный, будут эндотермическими.
Как рассчитывается энтальпия?
Как мы видели, основа энтальпии очень проста. Если его изменение отрицательное, рассматриваемая химическая реакция будет выделять тепловую энергию в среду. И если его изменение положительное, он будет поглощать энергию в виде тепла. Как мы можем это вычислить? Тоже очень просто.
Формула для расчета энтальпии выглядит следующим образом:
H = E + PV
Тем не менее, как мы уже сказали, что действительно интересует нас для определения термического поведения реакции, так это изменение энтальпии. Таким образом, мы находим эту новую формулу:
ΔH = ΔE + PΔV
Таким образом, если результат добавления изменения энергии к произведению давления и изменения объема положительный, это означает, что энтальпия увеличивается и, следовательно, тепловая энергия поступает в систему (это эндотермический эффект). Если, наоборот, результат этой суммы отрицательный, это означает, что энтальпия уменьшается на протяжении реакции и, следовательно, тепловая энергия покидает систему (она экзотермична).
Какие бывают типы энтальпии?
Мы уже точно видели, что такое энтальпия и как она рассчитывается. Теперь пришло время посмотреть, как он классифицируется в соответствии с природой химических реакций, которые он определяет, и как он влияет на тепловую энергию в них.
1. Энтальпия образования
Энтальпия образования определяется как количество энергии, необходимое для образования одного моля соединения (единица, с помощью которой измеряется количество вещества и которая эквивалентна 6,023 x 10 ^ 23 атомов или молекул соединения) от элементов, которые составляют его при стандартных условиях температуры и давления, то есть 25 ° C и 1 атмосфера соответственно.
2. Энтальпия разложения
Энтальпия разложения определяется как количество тепловой энергии, поглощаемой или выделяемой при один моль вещества распадается в его составных элементах.
3. Энтальпия горения
Энтальпия горения связана с горением веществ в присутствии кислорода. В этом смысле речь идет о энергия, выделяемая при сгорании одного моля вещества. Рассматриваемое вещество горит, когда вступает в реакцию с кислородом, и это экзотермические реакции, поскольку всегда выделяются тепло и свет.
4. Энтальпия гидрирования.
Энтальпия гидрирования определяется как энергия, выделяемая или поглощаемая, когда вещество мы добавляем молекулу водорода, чтобы обычно образовывать углеводород.
5. Энтальпия нейтрализации.
Энтальпия нейтрализации определяется как энергия, выделяемая или поглощаемая при смешивании кислоты (pH ниже 7) и основания (pH выше 7), которые в конечном итоге нейтрализуются. Отсюда и его название. Так долго как смесь кислотных и основных веществ, будет энтальпия нейтрализации, связанная с реакцией.
6. Энтальпия фазового перехода
Под энтальпией фазового перехода мы подразумеваем любое выделение или поглощение энергии, когда один моль определенного вещества изменить его агрегатное состояние. Другими словами, это энергия, связанная с изменением состояния между жидкостью, твердым телом и газом.
7. Энтальпия растворения
Энтальпия раствора определяется как энергия, поглощаемая или выделяемая при химическое вещество растворяется в водном растворе. То есть это энергия, связанная со смесью растворенного вещества и растворителя, имеющая ретикулярную фазу (поглощает энергию) и фазу гидратации (выделяет энергию).
8. Энтальпия плавления.
9. Энтальпия испарения.
10. Энтальпия сублимации.
11. Энтальпия затвердевания.
Как энтальпия связана с энтропией?
С другой стороны, энтропия прямо противоположна. И хотя неправильно определять его как величину, которая измеряет степень беспорядка в системе, верно, что это связано с энергией, недоступной в реакции. Таким образом, это определенным образом связано с молекулярным хаосом.
В любом случае энтальпия и энтропия связаны. Но каким образом? Что ж, правда в том, что это довольно сложно, но мы могли бы резюмировать это в следовать обратно пропорциональной зависимости: чем выше энтальпия (больше энергообмена), тем ниже энтропия (меньше беспорядка); при этом чем ниже энтальпия (меньше энергообмена), тем выше энтропия (больше беспорядка).
История эргономики: от истоков до наших дней
Энтальпия идеального газа не зависит от его давления или объема и зависит только от его температуры, которая коррелирует с его тепловой энергией. Реальные газы при обычных температурах и давлениях часто очень близки к этому поведению, что упрощает практическое термодинамическое проектирование и анализ.
СОДЕРЖАНИЕ
Определение
Энтальпия H термодинамической системы определяется как сумма ее внутренней энергии U и работы, необходимой для достижения ее давления и объема:
Добавление d ( pV ) к обеим сторонам этого выражения дает
Другие выражения
Приведенное выше выражение dH в терминах энтропии и давления может быть незнакомо некоторым читателям. Однако есть выражения для более знакомых переменных, таких как температура и давление:
В более общем виде первый закон описывает внутреннюю энергию с дополнительными членами, включающими химический потенциал и количество частиц различных типов. Тогда дифференциальное выражение для dH становится
Характерные функции
Физическая интерпретация
Отношение к теплу
Приложения
Теплота реакции
Полная энтальпия системы не может быть измерена напрямую; изменение энтальпии из системы измеряется вместо этого. Изменение энтальпии определяется следующим уравнением:
Удельная энтальпия
Изменения энтальпии
Изменение энтальпии описывает изменение энтальпии, наблюдаемое в составляющих термодинамической системы, когда происходит преобразование или химическая реакция. Это разница между энтальпией после завершения процесса, то есть энтальпией продуктов, предполагающей, что реакция идет до завершения, и начальной энтальпией системы, а именно реагентов. Эти процессы определяются исключительно их начальным и конечным состояниями, так что изменение энтальпии для обратного процесса является отрицательным по сравнению с изменением энтальпии для прямого процесса.
Открытые системы
В термодинамических открытых системах масса (вещества) может вливаться в границы системы и выходить из них. Первый закон термодинамики для открытых систем гласит: увеличение внутренней энергии системы равно количеству энергии, добавленной к системе за счет втекающей массы и нагревания, за вычетом количества, теряемого за счет истечения массы и в форме работы, выполненной системой:
Эти два типа работы выражаются уравнением
Подстановка контрольного объема (cv) в приведенное выше уравнение дает:
Определение энтальпии H позволяет нам использовать этот термодинамический потенциал для учета как внутренней энергии, так и работы pV в жидкостях для открытых систем:
Если мы позволим также границе системы перемещаться (например, из-за движущихся поршней), мы получим довольно общую форму первого закона для открытых систем. В терминах производных по времени он гласит:
с суммами по различным местам k, куда поступает тепло, в систему течет масса и границы движутся. Члены Ḣ k представляют потоки энтальпии, которые можно записать как
где угловые скобки обозначают средние по времени. Техническое значение энтальпии напрямую связано с ее присутствием в первом законе для открытых систем, сформулированном выше.
Диаграммы
Некоторые базовые приложения
Точки от a до h на рисунке играют важную роль в обсуждении в этом разделе.
| Точка | Т (К) | p (бар) | с ( кДж / (кг · К) ) | ч (кДж / кг) |
|---|---|---|---|---|
| а | 300 | 1 | 6,85 | 461 |
| б | 380 | 2 | 6,85 | 530 |
| c | 300 | 200 | 5,16 | 430 |
| d | 270 | 1 | 6,79 | 430 |
| е | 108 | 13 | 3,55 | 100 |
| ж | 77,2 | 1 | 3,75 | 100 |
| грамм | 77,2 | 1 | 2,83 | 28 год |
| час | 77,2 | 1 | 5,41 | 230 |
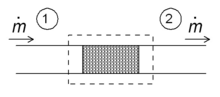
Дросселирование
Для установившегося режима потока энтальпия системы (пунктирный прямоугольник) должна быть постоянной. Следовательно
Поскольку массовый расход постоянен, удельные энтальпии по обе стороны от гидравлического сопротивления одинаковы:
Компрессоры
Минимальная мощность, необходимая для сжатия, достигается, если сжатие является обратимым. В этом случае второй закон термодинамики для открытых систем дает
Устранение Q̇ дает минимальную мощность
Соотношение для мощности можно еще более упростить, записав его как
При dh = T ds + v dp это приводит к окончательному соотношению
История
До 1920-х годов символ H использовался несколько непоследовательно для обозначения «тепла» в целом. Определение H как строго ограниченного энтальпией или «теплосодержанием при постоянном давлении» было формально предложено Альфредом В. Портером в 1922 году.
Энергетика химических процессов. Энтальпия, законы термодинамики
» data-shape=»round» data-use-links data-color-scheme=»normal» data-direction=»horizontal» data-services=»messenger,vkontakte,facebook,odnoklassniki,telegram,twitter,viber,whatsapp,moimir,lj,blogger»>
Энергетика химических процессов
Науку о взаимных превращениях различных видов энергии называют термодинамикой. Термодинамика устанавливает законы этих превращений, а также направление самопроизвольного течения различных процессов в данных условиях.
5.1. Общие понятия. При протекании химических реакций изменяется энергетическое состояние системы, в которой идет эта реакция. Состояние системы характеризуется термодинамическими параметрами (р, Т, с и др.). При изменении параметров меняется и состояние системы. В термодинамике свойства системы рассматриваются при ее равновесном состоянии. Термодинамическое состояние системы называют равновесным в том случае, когда его термодинамические параметры одинаковы во всех точках системы и не изменяются самопроизвольно (без затраты работы) во времени. Термодинамика изучает переходы системы из одного состояния в другое. Но переходы должны осуществляться при термодинамическом равновесии с окружающей средой, т.е. очень медленно, а в идеале — бесконечно медленно. При этом могут изменяться все параметры состояния системы, либо некоторые параметры остаются без изменения. Если процессы перехода системы происходят при постоянстве каких-то параметров системы, то они называются:
а) изобарическими (р = const);
б) изохорическими (Т= const);
в) изотермическими (Т = const);
г) изобарно-изотермическими (р,T – const) и т.д.
Термодинамика изучает возможность или невозможность самопроизвольного перехода системы из одного состояния в другое и энергетические эффекты этих переходов. Скорость и механизм процессов перехода — это области химической кинетики.
5.2. Внутренняя энергия. Первый закон термодинамики. При химических реакциях происходят глубокие качественные изменения в системе, рвутся связи в исходных веществах и возникают новые связи в конечных продуктах. Эти изменения сопровождаются поглощением или выделением энергии. В большинстве случаев этой энергией является теплота. Раздел термодинамики, изучающий тепловые эффекты химических реакций, называют термохимией. Реакции, которые сопровождаются выделением теплоты, называют экзотермическими, а те, которые сопровождаются поглощением теплоты, — эндотермическими. Теплота реакции является, таким образом, мерой изменения свойств системы, и знание ее может иметь большое значение при определении условий протекания той или иной реакции.
При любом процессе соблюдается закон сохранения энергии как проявление более общего закона природы — закона сохранения материи. Теплота Q, поглощенная системой, идет на изменение ее внутренней энергии и на совершение работы А:
Количественное соотношение между изменением внутренней энергии, теплотой и работой устанавливает первый закон термодинамики:
Уравнение означает, что теплота, подведенная к системе, расходуется на приращение внутренней энергии системы и на работу системы над окружающей средой.
Внутренняя энергия системы U — это общий ее запас, включающий энергию поступательного и вращательного движений молекул, энергию внутримолекулярных колебаний атомов и атомных групп, энергию движения электронов, внутриядерную энергию и т.д. Внутренняя энергия — полная энергия системы без потенциальной энергии, обусловленной положением системы в пространстве, и без кинетической энергии системы как целого. Абсолютное значение внутренней энергии U веществ неизвестно, так как нельзя привести систему в состояние, лишенное энергии. Внутренняя энергия, как и любой вид энергии, является функцией состояния, т.е. ее изменение однозначно определяется начальным и конечным состояниями системы и не зависит от пути перехода, по которому протекает процесс:
где: U – изменение внутренней энергии системы при переходе из начального состояния U1 в конечное U2. Если U2 > U1, то U> 0.
Если U2 0 (Н2 > Н1). В дальнейшем тепловые эффекты всюду выражаются через H.
5.4. Термохимические расчеты. Термохимические расчеты основаны на законе Гесса, позволяющее рассчитать энтальпию химической реакции: тепловой эффект реакции зависит только от природы и физического состояния исходных веществ и конечных продуктов, но не зависит от пути перехода.
Часто в термохимических расчетах применяют следствие из закона Гесса: тепловой эффект реакции (Нx.p.) равен сумме теплот образования Нобр продуктов реакции за вычетом суммы теплот образования исходных веществ с учетом коэффициентов перед формулами этих веществ в уравнении реакции:
Пример 1. При взаимодействии кристаллов хлорида фосфора (V) с парами воды образуется жидкий РОС13 и хлороводород. Реакция сопровождается выделением 111,4 кДж теплоты. Напишите термохимическое уравнение этой реакции.
Решение. Уравнения реакций, в которых около символов химических соединений указываются их агрегатные состояния или кристаллическая модификация, а также числовое значение тепловых эффектов, называют термохимическими. В термохимических уравнениях, если это специально не оговорено, указываются значения тепловых эффектов при постоянном давлении Qp, равные изменению энтальпии системы Н. Значение Н приводят обычно в правой части уравнения, отделяя его запятой или точкой с запятой. Приняты следующие сокращенные обозначения агрегатного состояния вещества: г — газообразное, ж — жидкое, к — кристаллическое. Эти символы опускаются, если агрегатное состояние веществ очевидно.
Вычислите теплоту образования этана, если известны теплоты образования СO2(г) и Н2O(ж) (см. табл. 15).
Решение. Теплотой образования (энтальпией) данного соединения называют тепловой эффект реакции образования 1 моль этого соединения из простых веществ, взятых в их устойчивом состоянии при данных условиях.
Обычно теплоту образования относят к стандартному состоянию, т.е. 25° С (298 К) и 1,01310 5 Па и обозначают через.Так как тепловой эффект с температурой изменяется незначительно, то в дальнейшем индексы опускаются и тепловой эффект обозначается через Н. Следовательно, нужно вычислить тепловой эффект реакции, термохимическое уравнение которой имеет вид
исходя из следующих данных:
На основании закона Гесса с термохимическими уравнениями можно оперировать так же, как и с алгебраическими. Для получения искомого результата следует уравнение (б) умножить на 2, уравнение (в) — на 3, а затем сумму этих уравнений вычитают из уравнения (а):
∆H =-1559,87-2(-393,51)-3(-285,84)= +84,67 кДж;
К тому же результату придем, если для решения задачи применить вывод из закона Гесса:
Учитывая, что теплоты образования простых веществ условно приняты равными нулю
Пример 3. Реакция горения этилового спирта выражается термохимическим уравнением
Вычислите тепловой эффект реакции, если известно, что молярная теплота парообразования С2Н5OН(ж) равна +42,36 кДж, а теплоты образования С2Н5OН(г), СO2(г), Н2O(ж) см. табл. 15.
Решение. Для определения Н реакции необходимо знать теплоту образования С2Н5OН(ж). Последнюю находим из данных:
Вычисляем H реакции, применяя следствие из закона Гесса:
5.5. Химическое сродство. Энтропия химических реакций. Энергия Гиббса. Самопроизвольно могут протекать реакции, сопровождающиеся не только выделением, но и поглощением теплоты.
Реакция, идущая при данной температуре с выделением теплоты, при другой температуре проходит с поглощением теплоты. Здесь проявляется диалектический закон единства и борьбы противоположностей. С одной стороны, система стремится к упорядочению (агрегации), к уменьшению Н; с другой стороны, система стремится к беспорядку (дезагрегации). Первая тенденция растет с понижением, а вторая — с повышением температуры. Тенденцию к беспорядку характеризует величина, которую называют энтропией.
Энтропия S, так же как внутренняя энергия U, энтальпия Н, объем V и др., является свойством вещества, пропорциональным его количеству. S, U, H, V обладают аддитивными свойствами, т.е. при соприкосновении системы суммируются. Энтропия отражает движение частиц вещества и является мерой неупорядоченности системы. Она возрастает с увеличением движения частиц: при нагревании, испарении, плавлении, расширении газа, при ослаблении или разрыве связей между атомами и т.п. Процессы, связанные с упорядоченностью системы: конденсация, кристаллизация, сжатие, упрочнение связей, полимеризация и т.п.— ведут к уменьшению энтропии. Энтропия является функцией состояния, т.е. ее изменение зависит только от начального (S1) и конечного (S2) состояний и не зависит от пути процесса:
Так как энтропия увеличивается с повышением температуры, то можно считать, что мера беспорядка равна TS. Энтропия выражается в Дж/(моль.К).
Таким образом, движущая сила процесса складывается из двух сил: стремления к упорядочению (Н) и стремления к беспорядку (TS). При р = const и Т = const общую движущую силу процесса, которую обозначают G, можно найти из соотношения
где: величина G называется изобарно-изотермическим потенциалом или энергией Гиббса.
Мерой химического сродства является убыль энергии Гиббса (G), которая зависит от природы вещества, его количества и температуры.
Энергия Гиббса является функцией состояния, поэтому
Самопроизвольно протекающие процессы идут в сторону уменьшения потенциала и, в частности, в сторону уменьшения G. Если G 0, процесс самопроизвольно проходить не может. Чем меньше G, тем сильнее стремление к протеканию данного процесса и тем дальше он от состояния равновесия, при котором G = 0 и H= TS.
Из соотношения G = H – TS видно, что самопроизвольно могут протекать и процессы, для которых H>0 (эндотермические). Это возможно, когда S>0, но |TS| > |H| и тогда G 0.
5.6. Второй и третий законы термодинамики. Для систем, которые не обмениваются с окружающей средой ни энергией, ни веществом (изолированные системы), второй закон термодинамики имеет следующую формулировку: в изолированных системах самопроизвольно идут только такие процессы, которые сопровождаются возрастанием энтропии: AS > 0.
Второй закон термодинамики имеет статистический характер, т.е.
справедлив лишь для систем, состоящих из очень большого числа
частиц.
Однако, если в системе протекает химическая реакция, то система обменивается энергией с окружающей средой, т.е. не является изолированной. Химические реакции обычно сопровождаются изменением как энтропии, так и энтальпии.
В отличие от других термодинамических функций, можно определить не только изменение, но абсолютное значение энтропии. Это вытекает из высказанного в 1911 г. М. Планком постулата, согласно которому «при абсолютном нуле энтропия идеального кристалла равна нулю». Этот постулат получил название третьего закона термодинамики.
Пример 1. В каком состоянии энтропия 1 моль вещества больше при одинаковой температуре: в кристаллическом или парообразном?
Решение. Энтропия есть мера неупорядоченности состояния вещества. В кристалле частицы (атомы, ионы) расположены упорядоченно и могут находиться лишь в определенных точках пространства, а для газа таких ограничений нет. Объем 1 моль газа гораздо больше объема 1 моль кристаллического вещества; возможность хаотичного движения молекул газа больше. А так как энтропию можно рассматривать как количественную меру хаотичности атомно-молекулярной структуры вещества, то энтропия 1 моль паров вещества больше энтропии 1 моль его кристаллов при одинаковой температуре.
Пример 2. Прямая или обратная реакция будет протекать при стандартных условиях в системе
Решение. ВычислимΔG 0 298 прямой реакции. Значения ΔG 0 298соответствующих веществ приведены в табл. 16. Зная, что ΔG есть функция состояния и что ΔG для простых веществ, находящихся в устойчивых при стандартных условиях агрегатных состояниях, равны нулю, находим ΔG 0 298процесса:
∆G 0 298 = 2 (-137,27) +2 (0) – (-50,79-394,38) = +170,63 кДж
То, что ΔG 0 298> 0, указывает на невозможность самопроизвольного протекания прямой реакции при Т = 298К и давлении взятых газов равном 1,013 ∙ 10 5 Па (760 мм рт. ст. = 1 атм).
Стандартная энергия Гиббса образования ΔG 0 298некоторых веществ
| Вещество | Состояние | ΔG 0 298, кДж/моль | Вещество | Состояние | ΔG 0 298, кДж/моль |
| ВаСО3 | к | -1138,8 | FeO | к | -244,3 |
| СаСО3 | к | -1128,75 | Н2О | ж | -237,19 |
| Fе3O4 | к | -1014,2 | Н2O | г | -228,59 |
| ВеСО3 | к | -944,75 | PbO2 | к | -219,0 |
| СаО | к | -604,2 | СО | г | -137,27 |
| ВеО | к | -581,61 | СН4 | г | -50,79 |
| NaF | к | -541,0 | NO2 | г | +51,84 |
| ВаО | к | -528,4 | NO | г | +86,69 |
| СО2 | г | -394,38 | C2H2 | г | +209,20 |
| NaCl | к | -384,03 | |||
| ZnO | к | -318,2 |
Стандартные абсолютные энтропии ΔS 0 298 некоторых веществ
| Вещество | Состояние | ΔS 0 298, Дж/(моль.К) | вещество | Состояние | ΔS 0 298,Дж/(моль.К) |
| С | Алмаз | 2,44 | Н2O | г | 188,72 |
| С | Графит | 5,69 | N2 | г | 191,49 |
| Fe | к | 27,2 | NН3 | г | 192,50 |
| Ti | к | 30,7 | СО | г | 197,91 |
| S | Ромб | 31,9 | с2H2 | г | 200,82 |
| TiO2 | к | 50,3 | O2 | г | 205,03 |
| FeO | к | 54,0 | H2S | г | 205,64 |
| H2O | ж | 69,94 | NO | г | 210,20 |
| Fе2О3 | к | 89,96 | CO2 | г | 213,65 |
| NH4C1 | к | 94,5 | C2H4 | г | 219,45 |
| СН3ОН | ж | 126,8 | Cl2 | г | 222,95 |
| Н2 | г | 130,59 | NO2 | г | 240,46 |
| Fе3O4 | к | 146,4 | РС13 | г | 311,66 |
| СН4 | г | 186,19 | PCl5 | г | 352,71 |
| НС1 | г | 186,68 |
Пример 3. На основании стандартных теплот образования (см. табл. 15) и абсолютных стандартных энтропий веществ (табл.17) вычислите ΔS 0 298 реакции, протекающей по уравнению
Решение. ∆G 0 = ∆H 0 – TS 0 ; ∆H и ∆S – функции состояния, поэтому
∆Н 0 х.р.=∑ ∆Н 0 прод – ∑ ∆Н 0 исх ; ∆S 0 x.p.= ∑S 0 прод – ∑ S 0 исх
∆Н 0 х.р.=(-393,51+0) – (110,52 – 285,84) = +2,85 кДж
∆S 0 x.p.=(213,65+130,59)-(197,91+69,94) = +76,39 = 0,07639 кДж/(моль∙К);
∆G 0 = +2,85 – 298 ∙ 0,07639 = – 19,91 кДж
Пример 4. Реакция восстановления Fе2О3 водородом протекает по уравнению
Возможна ли эта реакция при стандартных условиях, если изменение энтропии S=0,1387 кДж/(мольК)? При какой температуре начнется восстановление Fе2О3?
Решение. Вычисляем ∆G 0 реакции:
∆G = ∆Н-Т∆S = 96,61 – 298 ∙ 0,1387 = +55,28 кДж
Так как ∆G > 0, то реакция при стандартных условиях невозможна; наоборот, при этих условиях идет обратная реакция окисления железа (коррозия). Найдем температуру, при которой∆G=0:
Следовательно, при температуре 696,5 К начнется реакция восстановления Fе2О3 Иногда эту температуру называют температурой начала реакции.
Возможна ли реакция восстановления Fе2О3 углеродом при 500 и 1000 К?
Решение. ∆H 0 xp и ∆S 0 xp находим из соотношений (1) и (2) (см. разделы «Энергетика химических процессов. Термохимические расчеты» и «Химическое сродство»):
∆S 0 x.p.=(2 ∙ 27,2+3 ∙ 197,91) – (89,96+3 ∙ 5,69) = 541,1 Дж/(моль ∙ К)
Энергию Гиббса при соответствующих температурах находим из соотношения