какую прямую называют координатной

Координатная прямая

Урок 30. Математика 6 класс ФГОС

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Координатная прямая»

Представим себе такую историю…

– Привет, Паша! Над чем это ты так задумался? – поинтересовался у друга Саша.

– Я не могу решить одну задачу. Давай подумаем вместе, – обратился Паша к Саше.

– Давай. Читай условие, – сказал Саша.

– Гусеница сползает с листочка на веточку и ползает по ней влево и вправо. Где окажется гусеница, если она удалится на 5 сантиметров от листочка? – зачитал условие задачи Паша.

– И что же здесь сложного? – удивился Саша. – Всё просто. Гусеница окажется в 5 сантиметрах от листочка.

– Да, верно. Она окажется в 5 сантиметрах от листочка. Но она же ползает по веточке как влево, так и вправо. А значит, важно знать и направление, – сказал Паша.

– Точно, – согласился Саша. – И как же нам ответить на вопрос задачи?

– Давай спросим у Мудряша, – сказал Паша.

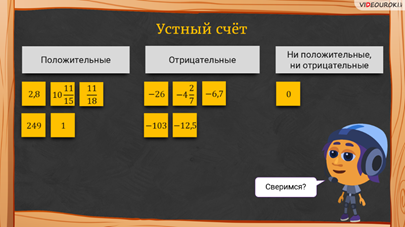
– Ребята, прежде чем я отвечу на ваш вопрос, давайте мы немного разомнёмся и выполним устные задания, – предложил Мудряш.

– Теперь сверимся! – сказал Мудряш. – Посмотрите, что у вас должно было получиться!

– А сейчас вернёмся к вашей задаче, – начал Мудряш. – Ребята, вы правильно заметили, что для того, чтобы ответить на вопрос задачи, нам надо знать направление, в котором ползёт гусеница.

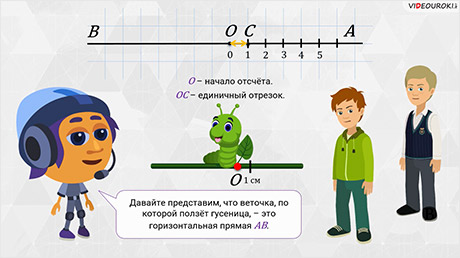
– Давайте представим, что веточка, по которой ползает гусеница, – это горизонтальная прямая АВ. Листочек на веточке, с которого сползает гусеница, обозначим на этой прямой точкой О и назовём началом отсчёта. Точка О будет изображать число 0 на нашей прямой. Можно сказать, что она разделяет прямую АВ на два луча – ОА и ОB. Предположим, что наша гусеница решила ползти вправо. Тогда отметим на луче ОА точку С, которая будет изображать число 1. Отрезок ОС – это единичный отрезок. На веточке это будет соответствовать 1 сантиметру. На луче ОА можно продолжить изображать положительные числа: 2, 3, 4, 5 и так далее.

– В 5 классе мы научились изображать на координатном луче положительные числа и 0, – дружно сказали Паша и Саша.

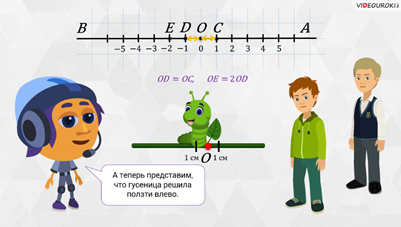
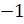
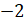
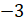
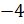
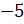
– Совершенно верно, – сказал Мудряш. – Это вам знакомо. А теперь представим, что гусеница решила ползти влево. Давайте на луче ОВ отметим точку D таким образом, чтобы отрезок OD был равен отрезку ОC. На веточке это также будет соответствовать 1 сантиметру. Будем считать, что точка D изображает число . Чтобы изобразить число , мы на луче ОB отметим точку Е таким образом, чтобы отрезок ОЕ был равен двум отрезкам ОD. Таким же образом мы можем продолжить изображать отрицательные числа: , , и так далее…

Говорят, что луч ОА задаёт положительное направление на прямой АВ.

– А тогда луч ОВ задаёт отрицательное направление на прямой АВ, – дружно сказали мальчишки.

– Всё верно, ребята! Отметим, что положительное направление указывают стрелкой, – добавил Мудряш.

– Получается, что на прямой АВ мы выбрали начало отсчёта – точку О, единичный отрезок ОС и направление, – отметили ребята.

– Да, и такую прямую мы будем называть координатной прямой, – сказал Мудряш.

– А тогда число, которое показывает положение точки на прямой, называют координатой этой точки? – задали вопрос Мудряшу Паша и Саша.

– Всё верно! – ответил Мудряш.

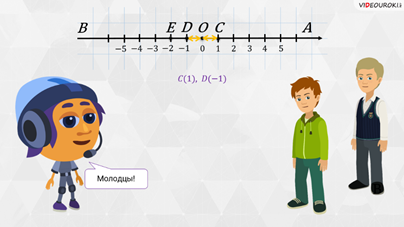
– Тогда координата точки С – это 1, а координата точки ДЭ – это 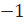, – добавили мальчишки.

– Молодцы! – похвалил ребят Мудряш и отметил, – записывают это вот так: точка С (1), точка D ().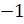

– Запомните! – продолжил Мудряш. – Прямую, на которой выбрали начало отсчёта, единичный отрезок и направление, называют координатной прямой. Число, показывающее положение точки на прямой, называют координатой этой точки.

– Тогда если наша гусеница проползёт 5 сантиметров вправо, то она окажется в точке с координатой 5? – вернулись к задаче ребята.

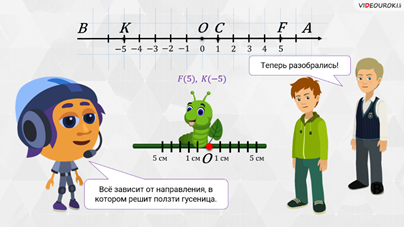
– Да! И мы можем назвать эту точку, например, точкой F и записать F (5), – сказал Мудряш.

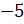
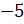
– А если гусеница проползёт 5 сантиметров влево, то окажется в точке с координатой , – продолжили Паша и Саша. – Давайте назовём её точкой K и запишем K ().

– Давайте, – согласился Мудряш.

– Тогда получается, что на вопрос задачи мы можем дать два ответа? – задали вопрос Мудряшу мальчики.

– Конечно! Всё зависит от того, в каком направлении решит ползти гусеница, – ответил на вопрос Мудряш.

– Теперь разобрались! – радостно сказали друзья.

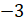
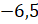
– Отметим на координатной прямой ещё несколько точек, – предложил Мудряш. – Например, точку М (), точку N (4), точку P ()… Но вместо слов «отметим точку с координатой…» может говорить просто «отметим число…».

– Запомните! – сказал Мудряш. – Все положительные числа и нуль называют неотрицательными числами. Все отрицательные числа и нуль называют неположительными числами.

– Ребята, хотелось бы обратить внимание на то, – продолжил Мудряш, – что координатная прямая может быть расположена не только горизонтально, как мы с вами только что рассмотрели, но и, например, вертикально. В таком случае положительными считаются координаты точек, находящихся выше точки О, а отрицательными – координаты точек, находящихся ниже точки О.

– Мне кажется, что шкала термометра, о которой мы говорили на прошлом уроке, является примером координатной прямой, – неуверенно сказал Паша.

– Правильно, – сказал Мудряш. – 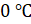– начало отсчёта. Положительные значения температуры расположены выше , а отрицательные – ниже . А теперь давайте выполним несколько заданий.

Задание первое: запишите координаты точек А, B, C, D, Е, изображённых на рисунке.

Решение: Единичный отрезок равен одной клеточке. Точка А находится на расстоянии 4 единичных отрезков справа от начала отсчёта, а значит, имеет координату 4.

Точка B находится на расстоянии половины единичного отрезка слева от начала отсчёта, а значит, её координата равна .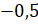

Точка C расположена на расстоянии 4 единичных отрезков слева от начала отсчёта, следовательно, имеет координату .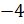

Точка D расположена на расстоянии 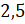единичных отрезков справа от начала отсчёта, следовательно, она имеет координату 2,5.

Точка Е находится на расстоянии 5,5 единичных отрезков слева от начала отсчёта, а значит, имеет координату .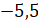

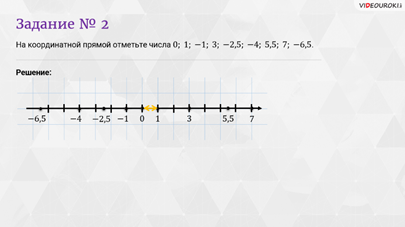
Второе задание: на координатной прямой отметьте числа: .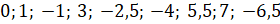

Решение: отметим число 0. Оно будет являться началом отсчёта. Отметим 1. Отрезок от 0 до 1 называем единичным отрезком.

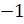
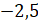
Число находится на расстоянии 1 единичного отрезка слева от начала отсчёта. Число 3 находится на расстоянии 3 единичных отрезков справа от начала отсчёта. Число находится слева от начала отсчёта на расстоянии 2,5 единичных отрезков.

Число находится слева от начала отсчёта на расстоянии 4 единичных отрезков.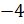

Число 5,5 расположено справа от начала отсчёта на расстоянии 5,5 единичных отрезков.

Число 7 также расположено справа от начала отсчёта, но на расстоянии 7 единичных отрезков.

И последнее число 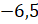расположено на расстоянии 6,5 единичных отрезков слева от начала отсчёта.

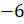
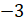
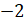
Следующее задание: длина единичного отрезка координатной прямой равна 1 см. Чему равно расстояние между точкой А (3) и точкой В (7), между точкой С () и точкой D (), между точкой Е () и точкой F (2)?

Решение: начертим координатную прямую, длина единичного отрезка которой равна одному сантиметру. Отметим точку А (3) и точку В (7). Расстояние между этими точками равно 4 единичным отрезкам, то есть 4 сантиметрам.

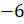
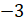
Теперь отметим точку С () и точку D (). Расстояние между ними равно 3 единичным отрезкам, то есть 3 сантиметрам.

Отметим точку Е (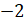) и точку F (2). Расстояние между этими точками равно 4 единичным отрезкам, а значит, 4 сантиметрам.

Ещё одно задание: в какую точку перейдёт точка С (3):

а) при перемещении на 4 единицы в положительном направлении;

б) при перемещении на 7 единиц в отрицательном направлении?

Решение: начертим координатную прямую АВ и отметим на ней точку С (3).

Положительное направление на прямой задаёт нам луч ОА. Значит при перемещении в положительном направлении, то есть вправо, на 4 единицы точка С перейдёт в точку К (7).

Отрицательное направление на прямой задаёт луч ОВ. Тогда при перемещении в отрицательном направлении, то есть влево, на 7 единиц точка С перейдёт в точку М ().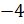

Источник

Координатная прямая (числовая прямая), координатный луч

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.

Координатный луч

Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.

На примере мы видим, что O является началом луча.

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.

Координатный луч – это шкала, которая может длиться до бесконечности.

Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.

Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.

Координатная прямая

Проведите луч в противоположную сторону, дополнив его до прямой

Отложите единичные отрезки по примеру, указанному выше

Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.

Соответствие между точками координатной прямой и действительными числами

Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.

Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.

Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.

Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.

Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.

Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.

Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.

Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.

Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.

Благодаря этому утверждению координатную прямую зачастую определяют как числовую.

Координаты точек на координатной прямой

Число, соответствующее точке на координатной прямой, называется координатой этой точки.

Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.

Источник

Координатная прямая (числовая прямая), координатный луч.

В этой статье мы определим координатный луч и координатную прямую. Сначала изобразим координатный луч и опишем, что он из себя представляет. Далее перейдем к координатной прямой, остановимся на взаимно однозначном соответствии между точками координатной прямой и действительными числами, откуда станет понятно, почему координатную прямую называют числовой прямой. В заключении поговорим о координатах точек на координатной прямой.

Прежде чем переходить дальше, нужно иметь представление о точке и прямой, а также знать геометрическую фигуру луч.

Навигация по странице.

Координатный луч

Так у нас есть луч. Как же его сделать координатным лучом?

В-третьих, на луче от конца единичного отрезка нужно отложить еще один отрезок, равный единичному, далее от конца этого отрезка нужно отложить еще один единичный отрезок, от конца построенного отрезка нужно отложить еще один единичный отрезок, и так далее.

Так координатный луч представляет собой не что иное, как бесконечную шкалу.

В этом случае подразумевается, что мы при необходимости можем легко продолжить построение шкалы, последовательно откладывая единичные отрезки на луче.

Также допускается буквы O и X записывать над лучом, а числа – под лучом.

Координатная прямая

Координатную прямую очень легко построить, если Вы хорошо усвоили принцип изображения координатного луча, о котором мы говорили в предыдущем пункте. Сделаем это.

На практике чаще используется координатная прямая, на которой отмечено лишь начало отсчета и единичный отрезок, то есть, координатная прямая одного из следующих видов.

Итак, координатная прямая – это прямая, на которой выбрано начало отсчета, указан единичный отрезок и задано направление.

Взаимно однозначное соответствие между точками координатной прямой и действительными числами

Нам известно, что на данной прямой линии лежит бесконечно много точек. Не является исключением и координатная прямая – она также содержит бесконечно много точек. Между точками координатной прямой и действительными числами существует очень важная связь, которую называют взаимно однозначным соответствием. Эта связь выражается следующим утверждением: каждой точке координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.

Озвученное утверждение, несомненно, нуждается в пояснении.

Отметим какую-нибудь точку на координатной прямой. Какое действительное число ей соответствует?

Если эта точка совпадает с началом отсчета (точкой O ), то будем считать, что ей отвечает число нуль.

Так как элементами множества действительных чисел являются все числа, которые можно записать в виде конечных и бесконечных десятичных дробей, то вся вышеизложенная в этом пункте информация позволяет утверждать, что каждой точке координатной прямой мы поставили в соответствие конкретное действительное число, при этом понятно, что разным точкам соответствуют разные действительные числа.

Также достаточно очевидно, что это соответствие является взаимно однозначным. То есть, мы можем указанной точке на координатной прямой поставить в соответствие действительное число, но мы также можем по данному действительному числу указать конкретную точку на координатной прямой, которой отвечает данное действительное число. Для этого нам придется отложить от начала отсчета в нужном направлении определенное количество единичных отрезков, а также десятых, сотых и так далее долей единичного отрезка. Например, числу 703,405 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 703 единичных отрезка, 4 отрезка, составляющих десятую долю единичного, и 5 отрезков, составляющих тысячную долю единичного.

Итак, каждой точке на координатной прямой отвечает действительное число, и каждое действительное число имеет свое место в виде точки на координатной прямой. Вот почему координатную прямую очень часто называют числовой прямой.

Координаты точек на координатной прямой

Число, соответствующее точке на координатной прямой, называется координатой этой точки.

В предыдущем пункте мы сказали, что каждому действительному числу соответствует единственная точка на координатной прямой, поэтому, координата точки однозначно определяет положение этой точки на координатной прямой. Иными словами, координата точки однозначно задает эту точку на координатной прямой. С другой стороны каждой точке на координатной прямой соответствует единственное действительное число – координата этой точки.

Источник