какую полуокружность называют единичной вопросы
Единичная окружность
Единичная окружность в тригонометрии
Все процессы тригонометрии изучают на единичной окружности. Сейчас узнаем, какую окружность называют единичной и дадим определение.
Единичная окружность — это окружность с центром в начале прямоугольной декартовой системы координат и радиусом, равным единице.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат.
Радиус — отрезок, который соединяет центр окружности с любой точкой, лежащей на окружности, а также длина этого отрезка. Радиус составляет половину диаметра.
Единичную окружность с установленным соответствием между действительными числами и точками окружности называют числовой окружностью.
Поясним, как единичная окружность связана с тригонометрией.
В тригонометрии мы постоянно сталкиваемся с углами поворота. А углы поворота связаны с вращением по окружности.
Угол поворота — это угол, который образован положительным направлением оси OX и лучом OA.
Величины углов поворота не зависят от радиуса окружности, по которой происходит вращение, поэтому удобно работать именно с окружностью единичного радиуса. Это позволяет избавиться от коэффициентов при математическом описании. Вот и все объяснение полезности единичной тригонометрической окружности.
Все углы, которые принадлежат одному семейству, дают одинаковые абсолютные значения тригонометрических функций, но эти значения могут различаться по знаку. Вот как:
Градусная мера окружности равна 360°. Чтобы решать задачи быстро, важно запомнить, где находятся углы 0°; 90°; 180°; 270°; 360°. Единичная окружность с градусами выглядит так:
Радиан — одна из мер для определения величины угла.
Один радиан — это величина угла между двумя радиусами, проведенными так, что длина дуги между ними равна величине радиуса.
Число радиан для полной окружности — 360 градусов.
Длина окружности равна 2πr, что превышает длину радиуса в 2π раза.
Поскольку по определению 1 радиан — это угол между концами дуги, длина которой равна радиусу, в полной окружности заключен угол, равный 2π радиан.
Потренируемся переводить радианы в градусы. В полной окружности содержится 2π радиан, или 360 градусов. Таким образом:
Кстати, определение синуса, косинуса, тангенса и котангенса в тригонометрии дается через координаты точек на единичной окружности. Эти определения дают возможность раскрыть свойства синуса, косинуса, тангенса и котангенса.
Уравнение единичной окружности
При помощи этого уравнения, вместе с определениями синуса и косинуса, можно записать основное тригонометрическое тождество:
Презентация по теме :»Синус,косинус и тангенс угла», 9-й класс.
Содержимое разработки
Синус, косинус и тангенс для угла от 0° до 180°
Не стыдно чего-нибудь не знать, но стыдно не хотеть учиться. (Сократ)
Какую полуокружность называют единичной?
Радиус равен 1,центр в начале координат, расположена в 1 и 2 координатной четверти.
Что называют синусом угла α, где 0°≤α≤180°
Синусом угла называется ордината точки
Что называют косинусом угла α, где 0°≤α≤180°
Косинусом угла называется абсцисса точки
В каких пределах находится значение синуса, косинуса?
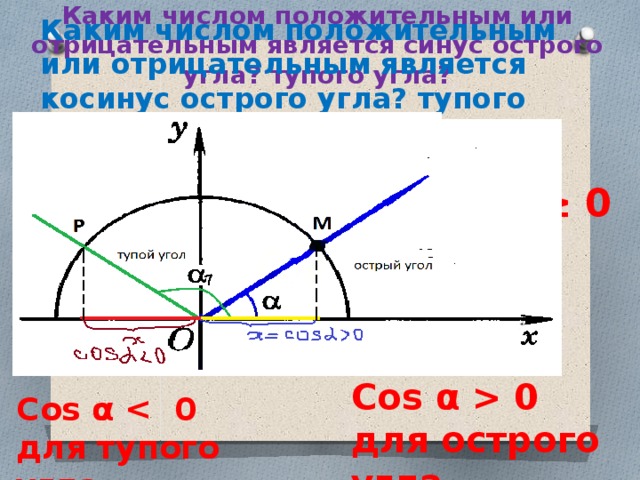
Каким числом положительным или отрицательным является косинус острого угла? тупого угла?
Каким числом положительным или отрицательным является синус острого угла? тупого угла?
Cos α 0 для острого угла
Какой формулой связаны синус и косинус одного и того же угла?
Основное тригонометрическое тождество
Что называют тангенсом угла α, где 0°≤α≤180 °
Тангенс – это отношение синуса к косинусу этого же угла(α≠90°)
Почему тангенс не определен для угла 90°?
х = cosα ≠ 0 значит α≠ 90°
Какое общее название имеют функции f(α) = sinα, g(α) = cosα, h(α) = tgα
Леонард Эйлер ввел и само понятие функции и принятую в наши дни символику.
Он придал всей тригонометрии ее современный вид.

В треугольнике АВС угол С равен 90°. ВС = 2
Геометрия
А Вы уже инвестируете?
Слышали про акцию в подарок?
Зарегистрируйся по этой ссылке
и получи акцию до 100.000 руб
План урока:
Тригонометрические функции тупых углов
Впервые с тригонометрическими функциями мы познакомились в 8 классе. Определить их значение можно было с помощью прямоугольного треугольника, рассматривая отношения его сторон (катетов и гипотенуз). Но такой способ определения тригонометрических функций подходит только для острых углов, попадающих в интервал от 0 до 90°. Оказывается, есть способ для вычисления значений тригонометрических функций и от больших углов.
Построим на координатной плоскости полуокружность, центр которой располагается в начале координат, а радиус равен единице. Ее называют единичной полуокружностью. Проведем из точки (0; 0) луч под некоторым углом α, который пересечет полуокружность в некоторой точке М с координатами (х; у). Заметим, что каждому значению α соответствует своя точка М на единичной полуокружности:
Опустим из М перпендикуляр на ось Ох в некоторую точку D. Тогда, если угол α острый,получается прямоугольный треугольник МOD, длины сторон которого можно определить так:
Получается, что координаты точки M как раз и являются синусом и косинусом угла α. Логично считать, что если α – не острый угол, то всё равно координаты точки M будут определять синус и косинус угла α.
Видно, что при тупом угле α точка М оказывается левее оси Оу, поэтому ее абсцисса становится отрицательной. Получается, что косинус может принимать отрицательные значения.
С помощью единичной полуокружности несложно выяснить значения синусов и косинусов для углов 0°, 90° и 180°. Они соответствуют координатам точек А, В и С на рисунке:
Так как эти точки имеют координаты (1; 0), (0; 1) и (– 1; 0), то можно записать следующее:
Используя это определение, найдем тангенс для углов 0° и 180°:
Заметим, что для 90° использовать эту формулу не удастся, так как это приведет к делению на ноль. Поэтому считается, что для 90° значение тангенса не определено, то есть его нельзя вычислить.
Единичная полуокружность является дугой окружности, чей радиус равен единице, а центр находится в начале координат. То есть она может быть задана уравнением
Тем самым мы доказали, что это тождество, которое показывает связь тригонометрических функций друг с другом, выполняется не только для острых углов, но и для всех углов из диапазона 0° ≤α ≤ 180°.
Для вычисления значений тригонометрических углов тупых углов удобно пользоваться так называемыми формулами приведения. Их довольно много, и изучаются они в основном в 10 классе, нам же хватит всего двух формул:
Например, пусть надо вычислить синус для угла 120°. Для этого мы представляем угол в виде разности, где в качестве уменьшаемого используется угол 180°:
Убедиться в справедливости этих двух формул приведения можно с помощью такого построения:
Точка М соответствует углу α, а точка K – углу (180° – α). Опустим из этих точек перпендикуляры МС и KD. Так как
Получается, что ∆OKD и ∆ОМС – прямоугольные, у них есть одинаковый острый угол α, и их гипотенузы ОК и ОМ также одинаковы как радиусы одной окружности. Тогда эти треугольники равны, и поэтому
Знак минус в первом из этих равенств показывает, что точки K отрицательная абсцисса. В итоге мы доказали две формулы приведения.
Задание. Вычислите sin 150°.
Решение. Представим угол 150° в виде разности:
Вычисление координат точки
Пусть есть некоторая точка А(х;у) с неотрицательной ординатой. Соединим ее с началом координат прямой, которая образует угол α с осью Ох. Посмотрим, как связаны координаты А со значением α.
Пусть луч ОА пересечет единичную окружность в точке М. Опустим из М и А перпендикуляры на Ох, в точки Н и С соответственно. Теперь сравним ∆ОМН и ∆ОАС. Они прямоугольные, и у них есть одинаковый угол α, следовательно, они подобны. Коэффициент подобия можно найти, поделив ОА на ОМ, при этом учтем, что ОМ = 1, так как М лежит на единичной полуокружности:
Примечание. Данное доказательство не рассматривает частные случаи, когда точка А лежит непосредственно на осях Ох и Оу, и тогда подобные треугольники ∆ОМН и ∆ОАС построить не удается. Эти случаи можно рассмотреть отдельно и показать, что для них выведенные формулы также справедливы.
Задание. Точка А находится на расстоянии 3 от начала координат (точки О), причем луч ОА образует с осью Ох угол 135°. Найдите координаты точки А.
Решение. Используя выведенные формулы, мы можем записать:
Вычисление площади треугольника
В 8 классе мы уже познакомились с одной из формул для определения площади треугольника. Однако на практике возникают ситуации, когда удобнее использовать другие формулы, одну из которых мы сейчас выведем.
Пусть в произвольном ∆АВС известны две стороны, например, ВС (обозначим ее буквой а) и АС (ее обозначим как b). Также известна величина угла между ними:
Разместим этот треугольник в системе координат так, чтобы точка С совпала с началом координат, в находилась на оси Ох и имела положительную абсциссу, А располагалась в первой четверти:
В этом случае координаты А будут определяться формулами:
Найдите площадь ∆МКН.
Решение. Подставляя числа в формулу, получаем:
Задание. Диагонали прямоугольника пересекаются под углом 30°, причем они равны 10 см. Вычислите площадь этого прямоугольника.
Заметим, что диагонали прямоугольника при пересечении образуют не один, а два угла. Пусть в прямоугольнике АВСD диагонали пересекаются в точке О, и ∠АОВ = 30°. Тогда можно найти ∠ВОС, ведь он смежный с ∠АОВ:
Чтобы найти площадь прямоугольника, мы можем найти площади 4 треугольников, из которых он состоит, и потом сложить их. Для каждого из этих треугольников нам известны две стороны (они составляют по 5 см) и угол между ними:
Площадь параллелограмма
Из выведенной нами формулы площади треугольника вытекает и новая формула для площади параллелограмма. Пусть в параллелограмме нам известны смежные и угол между ними:
На рисунке смежные стороны АВ и AD обозначены буквами a и b, а угол между ними обозначен как α. Проведем диагональ BD. Площадь ∆ABD можно вычислить:
Задание. Стороны параллелограмма имеют длины 8 и 11 см, а один из углов параллелограмма равен 30°. Какова площадь этого параллелограмма?
Решение. Просто подставляем данные в формулу
Задание. Известна площадь параллелограмма MNEF, одна из его сторон и угол:
Так как противоположные стороны в параллелограмме одинаковы, то MF также имеет длину 5:
Запишем формулу для площади и подставим в нее известные данные:
Теорема синусов
Пусть есть некоторый ∆АВС, в котором стороны мы обозначим буквами:
Посчитаем его площадь, используя стороны b и c:
Также площадь треугольника можно выразить через а и с:
Полученная формула показывает, что в каждом треугольнике отношение стороны к синусу противолежащего угла – это константа, не зависящая от выбора стороны. Другими словами,в любом треугольнике стороны пропорциональны синусам углов, которые лежат против них. Это утверждение именуют теоремой синусов.
В большинстве задач достаточно выведенной формулы
Однако можно дополнить теорему синусов, выяснив, чему же именно равны все эти три отношения. Для этого впишем треугольник в окружность, после чего построим диаметр BD:
Пусть радиус этой окружности равен R, тогда диаметр BD будет вдвое больше:
Теперь рассмотрим ∆ВСD. ∠С здесь – прямой, ведь это вписанный угол, опирающийся на полуокружность, то есть дугу в 180°. По определению синуса, которое мы давали ещё в 8 классе, можно записать:
C учетом уже выведенного равенства (6) теорема синусов примет вид:
С помощью теоремы синусов у любого треугольника можно найти две неизвестные стороны, если известны третья сторона и два угла. Процесс нахождение неизвестных элементов треугольника по уже известным элементам именуется решением треугольника. Всего у треугольника 6 элементов – три стороны и три угла. Для нахождения всех элементов в общем случае достаточно знать только 3 из них, а остальные можно найти, используя теорему синусов или иные геометрические соображения.
Задание. Решите треугольник, если одна из его сторон равна 14, а прилегающие к ней углы имеют величину 60° и 40°.
Обозначим описанный в условии треугольник как ∆МВК. Пусть МК = 14, ∠М = 60° и∠К = 40°. Тогда нам надо найти ∠В, МВ и ВК. Проще всего найти∠В, ведь в любом треугольнике все углы в сумме дают 180°:
Обратите внимание, что так как углы 40° и 80° не являются табличными, то их значения надо вычислять на калькуляторе, а результат вычисления получается приближенным. В данном случае мы округлили его до сотых.
Осталось найти сторону ВК, это также делается с помощью теоремы синусов:
Задание. В ∆SRT∠S = 30°, ∠R = 45°, а высота RM, опущенная на сторону TS, имеет длину 6. Решите ∆SRT.
Теперь надо найти какую-нибудь сторону в ∆SRT. Для этого рассмотрим ∆RMS. Он прямоугольный, а потому для него можно записать:
Для нахождения двух оставшихся сторон можно использовать теорему синусов:
Задание. В параллелограмме MNEF∠MFE составляет 120°, а диагональ NF равна 24 и образует со стороной NE угол 40°. Найдите длину МN и MF.
Далее заметим, что ∠FNE и ∠MFN одинаковы, ведь они накрест лежащие при параллельных отрезках NE и MF и секущей NF:
Теперь в ∆MNF известна сторона NF и все три угла. Это позволяет с помощью теоремы синусов найти и остальные две стороны:
Задание. В окружности радиусом 5 построен вписанный угол величиной 30°. Определите длину хорды, на которую он опирается.
Решение. По теореме синусов мы можем записать, что
Теорема косинусов
Теорема синусов помогает решать треугольники, в которых известны хотя бы два угла, а также одна из сторон. Но что делать в случае, если наоборот, даны две стороны, но только один угол? Здесь необходима другая теорема, которую именуют теоремой косинусов.
Возьмем произвольный треугольник со сторонами а, b и c и поместим его на координатной плоскости так, как показано на рисунке:
Обозначим угол между а и b как α. Тогда координаты А будут определяться так:
Точка В в свою очередь будет иметь координаты (а; 0). Зная координаты А и В, мы можем найти квадрат расстояния между ними, то есть величину с 2 :
Полученное соотношение как раз и является теоремой косинусов.
Данная формула позволяет находить третью сторону треугольника, если известны две другие, а также угол между ними. Однако ее можно переписать так, чтобы с ее помощью можно было вычислять косинус угла, зная все три стороны треугольника:
Это позволяет решать те треугольники, для которых теоремы синусов недостаточно.
Легко заметить, что теорема косинусов похожа на теорему Пифагора. Более того, если угол α = 90°, то формула теоремы косинусов превращается в теорему Пифагора, которая, таким образом, является ее частным случаем. По этой причине иногда теорему косинусов именуют обобщенной теоремой Пифагора.
Задание. Решите ∆MNE, если
Решение. По теореме косинусов находим сторону NE:
Осталось найти ∠N и ∠Е. Для этого запишем теорему косинусов так, чтобы в ней фигурировал ∠N:
Мы нашли cosN. Чтобы вычислить сам ∠N, следует использовать особую функцию на калькуляторе или компьютере, которая называется арккосинусом и является обратной для операции «извлечение косинуса». Более подробно она изучается уже в 10 классе. С ее помощью мы узнаем, что
Обратите внимание, что обычно калькулятор выдает результат, показывая десятые и сотые доли градусы, не переводя их в минуты и секунды. Можно оставить ответ и в таком виде. При желании перевести сотые доли в минуты следует дробную часть умножить на 60:
Задание. На различных сторонах угла∠А, равного 45°, отложены точки В и С так что
Задание. Решите треугольник, если его стороны имеют длину 14, 18 и 20.
Решение. Здесь надо дважды применить теорему косинусов, чтобы найти какие-нибудь два угла в ∆АВС:
∠C также можно найти через теорему косинусов, но проще просто вычесть из 180° два уже вычисленных угла:
Во всех рассмотренных задачах на решение треугольника мы знали три элемента треугольника и по ним однозначно вычисляли три других элемента. Однако иногда это невозможно. Так, если в задаче помимо двух сторон указан угол, который НЕ лежит между ними, то в итоге задача может иметь два решения.
Задание. В ∆MNE ∠M составляет 60°, а стороны МЕ и NE имеют длины 10 и 9 соответственно. Какова длина MN?
Решение. Теорему синусов здесь применить не удастся, так как для нее необходимо знать хотя бы два угла. Поэтому остается только записать теорему косинусов так, чтобы в ней использовался ∠M:
Получили квадратное уравнение, решить его можно через дискриминант:
В рамках данного урока мы узнали про теоремы синусов и косинусов и научились использовать их для решения треугольников. Также мы познакомились с новыми формулами для вычисления площадей треугольника и параллелограмма.














