какую функцию выполняет сопло в ракете

СОДЕРЖАНИЕ

История

Атмосферное использование

Оптимальный размер сопла ракетного двигателя для использования в атмосфере достигается, когда выходное давление равно окружающему (атмосферному) давлению, которое уменьшается с увеличением высоты. Для ракет, летящих с Земли на орбиту, простая конструкция сопла оптимальна только на одной высоте, при этом теряется эффективность и расходуется топливо на других высотах.

Небольшое перерасширение вызывает небольшое снижение эффективности, но в остальном не приносит большого вреда. Однако, если давление на выходе меньше примерно 40% от давления окружающей среды, происходит «разделение потока». Это может вызвать нестабильность выхлопа, которая может вызвать повреждение форсунки, затруднения в управлении автомобилем или двигателем и, в более крайних случаях, разрушение двигателя.

Использование вакуума

Для форсунок, которые используются в вакууме или на очень большой высоте, невозможно сопоставить давление окружающей среды; скорее, форсунки с большей долей площадей обычно более эффективны. Однако очень длинное сопло имеет значительную массу, что само по себе является недостатком. Обычно необходимо подобрать длину, которая оптимизирует общие характеристики автомобиля. Кроме того, когда температура газа в сопле снижается, некоторые компоненты выхлопных газов (например, водяной пар от процесса сгорания) могут конденсироваться или даже замерзать. Это крайне нежелательно, и этого следует избегать.

сопло де Лаваля в одном измерении

Анализ потока газа через сопла де Лаваля включает ряд концепций и упрощающих предположений:

Линейную скорость выходящих выхлопных газов можно рассчитать с помощью следующего уравнения

Вот некоторые типичные значения скорости выхлопных газов v _e для ракетных двигателей, сжигающих различные виды топлива:

Интересно отметить, что v _e иногда называют идеальной скоростью выхлопного газа, поскольку она основана на предположении, что выхлопной газ ведет себя как идеальный газ.

В качестве примера расчета с использованием приведенного выше уравнения предположим, что пороховые газы сгорания: при абсолютном давлении входят в сопло p = 7,0 МПа и выходят из выхлопной трубы ракеты при абсолютном давлении p _e = 0,1 МПа; при абсолютной температуре Т = 3500 К; с коэффициентом изоэнтропического расширения γ = 1,22 и молярной массой M = 22 кг / кмоль. Использование этих значений в приведенном выше уравнении дает скорость выхлопа v _e = 2802 м / с или 2,80 км / с, что согласуется с приведенными выше типичными значениями.

Удельный импульс

а для форсунок с идеальным расширением ( p _e = p _o ) это сводится к:

я зр знак равно F м ˙ грамм о знак равно м ˙ v е м ˙ грамм о знак равно v е грамм о <\ displaystyle I _ <\ text > = <\ frac <<\ dot > \, g _ <\ text >>> = <\ frac <<\ dot > \, v _ <\ text >> <<\ dot > \, g _ <\ text >>> = <\ frac >> >>>>

которая представляет собой просто вакуумную тягу за вычетом силы окружающего атмосферного давления, действующей на выходную плоскость.

По существу, тогда для сопел ракет окружающее давление, действующее на двигатель, нейтрализуется, за исключением плоскости выхода ракетного двигателя в обратном направлении, в то время как выхлопная струя создает прямую тягу.

Аэростатическое противодавление и оптимальное расширение

По мере того, как газ движется вниз по расширяющейся части сопла, давление и температура уменьшаются, а скорость газа увеличивается.

Если давление на выходе слишком низкое, струя может отделиться от сопла. Это часто нестабильно, и струя обычно вызывает большие смещения оси и может механически повредить сопло.

Это разделение обычно происходит, если давление на выходе падает ниже примерно 30–45% от окружающего, но разделение может быть отложено до гораздо более низких давлений, если сопло спроектировано так, чтобы увеличивать давление на ободе, как это достигается с SSME (1–2 psi при окружающем давлении 15 psi).

Кроме того, когда ракетный двигатель запускается или дросселируется, давление в камере меняется, и это обеспечивает разные уровни эффективности. При низком давлении в камере двигатель почти неизбежно будет чрезмерно расширен.

Оптимальная форма

Отношение площади самой узкой части сопла к площади выходной плоскости в основном определяет, насколько эффективно расширение выхлопных газов преобразуется в линейную скорость, скорость истечения и, следовательно, тягу ракетного двигателя. Свойства газа тоже имеют значение.

Форма сопла также незначительно влияет на то, насколько эффективно расширение выхлопных газов преобразуется в линейное движение. Самая простая форма сопла имеет половину угла конуса

15 °, что дает эффективность около 98%. Меньшие углы дают немного более высокую эффективность, большие углы дают меньшую эффективность.

Часто используются более сложные формы вращения, такие как сопла раструба или параболические формы. Они дают, возможно, на 1% больший КПД, чем коническое сопло, и могут быть короче и легче. Они широко используются на ракетах-носителях и других ракетах, где вес имеет большое значение. Их, конечно, сложнее изготовить, поэтому, как правило, они более дорогостоящие.

Также существует теоретически оптимальная форма сопла для максимальной скорости выхлопа. Однако обычно используется более короткая форма раструба, которая дает лучшие общие характеристики благодаря гораздо меньшему весу, меньшей длине, меньшим потерям сопротивления и лишь незначительно меньшей скорости выхлопа.

Другие аспекты конструкции влияют на эффективность сопла ракеты. Горловина сопла должна иметь ровный радиус. Внутренний угол, сужающийся к горловине, также влияет на общую эффективность, но он невелик. Угол выхода сопла должен быть как можно меньше (около 12 °), чтобы свести к минимуму вероятность проблем с разделением при низких давлениях на выходе.

Продвинутый дизайн

Форсунки с атмосферной границей включают:

Каждый из них позволяет сверхзвуковому потоку адаптироваться к окружающему давлению за счет расширения или сжатия, тем самым изменяя отношение выхода так, чтобы оно было на (или близко) оптимальном давлении на выходе для соответствующей высоты. Форсунки с пробкой и аэродинамическими шипами очень похожи в том, что они имеют радиальную проточную конструкцию, но форсунки с заглушкой имеют сплошное центральное тело (иногда усеченное), а сопла с шипами имеют «базовый отвод» газов для имитации твердого центрального тела. Сопла ED представляют собой сопла с радиальным выходом потока, поток которых отклоняется центральным стержнем.

Сопла с регулируемым разделением потока включают в себя:

Как правило, они очень похожи на колпачковые сопла, но включают в себя вставку или механизм, с помощью которого можно увеличивать соотношение площади на выходе при понижении давления окружающей среды.

Двухрежимные насадки включают:

Они имеют либо две горловины, либо две упорные камеры (с соответствующими горловинами). Центральная горловина имеет стандартную конструкцию и окружена кольцевой горловиной, через которую отводятся газы из той же (двухканальной) или отдельной (двухдетекторной) камеры тяги. В любом случае оба горловины будут выходить в сопло колокола. На больших высотах, где окружающее давление ниже, центральное сопло будет отключено, уменьшая площадь горловины и тем самым увеличивая соотношение площадей сопла. Эти конструкции требуют дополнительной сложности, но преимущество наличия двух осевых камер состоит в том, что они могут быть сконфигурированы для сжигания различных ракетных топлив или различных соотношений топливной смеси. Аналогичным образом, Aerojet также разработала сопло, называемое «Форсунка с усилением тяги», которая впрыскивает топливо и окислитель непосредственно в секцию форсунки для сгорания, что позволяет использовать форсунки с большим соотношением площадей глубже в атмосфере, чем они были бы без увеличения из-за эффектов разделение потоков. Они снова позволят использовать несколько порохов (например, РП-1), еще больше увеличивая тягу.

Источник

реактивное сопло

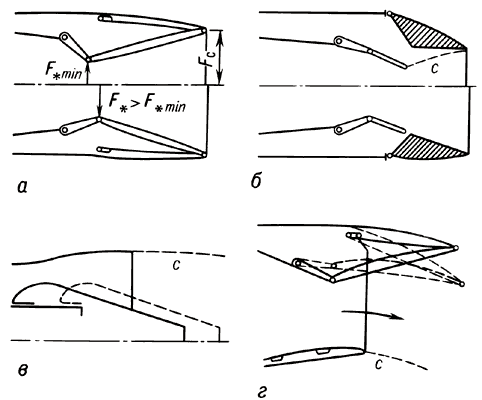
Схемы регулируемых реактивных сопел.

реакти́вное сопло́ — выходной канал реактивного двигателя, в котором происходит преобразование потенциальной энергии газа в его кинетическую энергию. Путём регулирования минимальной площади Р. с. F_* (см. рис.) достигается высокоэффективная работа расположенных перед ним элементов двигателя (газогенератора, форсажной камеры и др.). Течение в Р. c. должно происходить с минимальными потерями для получения максимальной тяги двигателя. Для достижения высоких лётных характеристик летательного аппарата на всех режимах полёта требуется точное согласование внутреннего контура Р. с. с внешними обводами силовой установки. Поэтому необходимо осуществлять не только указанное регулирование площади F_*, но и регулирование площади F_c выходного сечения Р. с.

С помощью Р. с. в ряде случаев управляют значением и направлением вектора тяги (см. Управление вектором тяги), реверсируют тягу, (см. Реверсивное устройство) и уменьшают шум, выходящий из Р. с. газовой струи. Конструкция Р. с. должна быть работоспособной при высокой температуре, обеспечивать герметичность и иметь малую массу.

Р. с. могут быть разделены на два типа: суживающиеся, в которых площадь поперечного сечения по длине уменьшается, и суживающиеся — расширяющиеся (типа Лаваля сопла), в которых площадь поперечного сечения по длине сначала уменьшается, а затем увеличивается. Их также различают по форме проходных сечений: круглые, кольцевые, прямоугольные («плоские») и др. Выбор формы сопла определяется многими факторами, главными из которых являются: рациональная (с наименьшим внешним сопротивлением) компоновка на летательном аппарате, возможность управления вектором тяги, снижение уровней ИК излучения, шума и т. п. Контуры Р. с. для уменьшения гидравлических потерь стремятся выполнить плавными. В этом случае потери обусловлены в основном тернием, и в первом приближении течение газа в Р. с. можно рассматривать изоэнтропическим и одновременным. В Р. с. с большими углами суживающейся и расширяющейся частей, при наличии угловых точек в его контуре, а также в Р. с. неосесимметричной формы течение нельзя считать одномерным. В этом случае возникают также газодинамические потери (например, в скачках уплотнения), определение которых возможно лишь в результате двух- и трёхмерных расчётов течения Р. с.

Истечение из суживающегося-расширяющегся сопла при больших степенях понижения давления ( = /p_н, где — полное давление газа перед соплом, p_н — давление в окружающей среде) происходит таким образом, что в выходном сечении Р. с. давление p_c не связано с давлением в окружающей среде и зависит только от , площадь выходного сечения F_с и формы сопла. Различают три режима истечения: расчётный — при p_c = p_н; перерасширение газа в сопле — при p_c p_н. Так как величина с увеличением скорости (Маха числа полёта M_∞) растёт от 2—3 при M_∞ = 0 до 20—25 при M_∞ = 3, то очевидно, что нерегулируемые Р. с. (F_c/F_* = const) лишь при одном значении работают на расчётном режиме. На всех остальных режимах имеются потери тяги, связанные с нерасчётностью истечений.

В большинстве случаев стенки регулируемых Р. с. двигателя выполняются из набора створок, которые имеют прямолинейные образующие — сужающаяся и расширяющаяся части представляют собой усечённые конусы, плавно соединяющиеся в окрестности минимального сечения сопла. В связи с этим, кроме указанных гидравлических и газодинамических потерь тяги, а также потерь из-за нерасчётности истечения возникают потери на непараллельность потока в выходном сечении сопла (потери на рассеивание потока) и потери, связанные с негерметичностью стенок и соединений в конструкции сопла (потери на утечки газа). В лучших образцах регулируемых Р. c. потери на утечки не превышают 5%.

Уровни потерь тяги в Р. c. на различных режимах работы двигателя описываются рядом коэффициентов, важнейшими из которых являются коэффициент тяги сопла _с и коэффициент эффективной тяги сопла

,

где P_c = ∫(p + ρv 2 )dF – p_нF_с — действительная тяга сопла, равная разности импульса на выходе из сопла и силы противодействия окружающей среды; P_ид = m_сv_ид — идеальная тяга сопла; v_ид — идеальная скорость истечения, соответствующая изоэнтропическому расширению газа от давления до давления p_н; m_c — масса газа, проходящего через сопло в 1 с, x_c — сила внешнего сопротивления сопла (кормовой части силовой установки); = P_c/P_ид. Значения _с для лучших регулируемых сопел равны 0,97—0,98.

Наиболее распространёнными схемами регулируемых Р. c. являются суживающиеся-расширяющиеся с непрерывным контуром и разрывом контура. Прорабатываются конструкции сопел с центральным телом и плоские. Показанные на рисунке схемы а и б иллюстрируют возможность независимого механического регулирования минимального и выходного сечения суживающегося-расширяющегося сопла и сопла с разрывом контура. Наличие «жидкой стенки» c у сопла с разрывом контура (б), сопла с центральным телом (в) и плоского сопла с односторонним внешним расширением (г) обеспечивает автоматическое аэродинамическое регулирование выходного сечения сопла (положение «жидкой стенки» зависит от ). Регулирование площади минимального сечения сопла в схеме сопла с центральным телом возможно либо путём осевого перемещения центрального тела, либо путём прикрытия обечайки, для чего конструкция её должна быть створчатой. В плоском Р. с. наиболее просто реализовать отклонение вектора тяги с помощью верхней створки, которая может быть одновременно дефлектором или закрылком крыла, что способствует повышению аэродинамического качества.

Масса конструкции сверхзвукового Р. с. с непрерывным контуром составляет примерно 10% массы двигателя.

Источник

Расчёт сопел современных ракетных двигателей

Введение

Сопло ракетного двигателя- техническое приспособление, которое служит для ускорения газового потока, проходящего по нему до скоростей, превышающих скорость звука. Основные виды профилей сопел приведены на рисунке:

По причине высокой эффективности ускорения газового потока, нашли практическое применение сопла Лаваля. Сопло представляет собой канал, суженный в середине. В простейшем случае такое сопло может состоять из пары усечённых конусов, сопряжённых узкими концами:

Ракета Поморцева приводилась в движение сжатым воздухом, что существенно ограничивало ее дальность, но зато делало ее бесшумной. Ракета предназначалась для стрельбы из окопов по вражеским позициям. Боеголовка оснащалась тротилом.

В ракете Поморцева было применено два интересных конструктивных решения: в двигателе имелось сопло Лаваля, а с корпусом был связан кольцевой стабилизатор. Подобные конструкции используются и в настоящее время, но уже с твёрдотопливным двигателем и системой автоматического наведения:

Однако проблемы остались старые, но уже в современном исполнении: ограниченная дальность до 3 км., наведение и удержание цели в условиях хорошей видимости, что для настоящего боя не реально, не защищённость от электромагнитных заградительных помех и, наконец, но не в последнюю очередь, высокая стоимость.

Теоретические основы

Эффективные сопла современных ракетных двигателей профилируются на основании специальных газодинамических расчётов. Основное уравнение, связывающее градиент площади сечения, градиент скорости и число Маха, следующее:

где: S – площадь сечения сопла; v – скорость газа; M – число Маха (отношение скорости газа в какой-либо точке потока к скорости звука в этой же точке).

Анализируя это соотношение, получаем, что в сопле Лаваля могут осуществляться следующие режимы течения:

1) M 0 (из уравнения). Дозвуковой поток в сужающемся канале ускоряется.
б) >0, тогда 1 – поток на входе сверхзвуковой:
а) 0, тогда >0. Сверхзвуковой поток в расширяющемся канале ускоряется.
3) = 0 – самое узкое место сопла, минимальное сечение.
Тогда возможно либо М = 1 (поток переходит через скорость звука), либо = 0 (экстремум скорости).

Какой из режимов реализуется на практике, зависит от перепада давлений между входом в сопло и окружающей средой.

Если давление, достигаемое в критическом сечении, превышает наружное давление, то поток на выходе из сопла будет сверхзвуковым. В противном случае он остается дозвуковым. [2]

— условие сверхзвукового истечения.

где: p* – давление торможения (давление в камере); pкр – давление в критическом сечении сопла; pнар – давление в окружающей среде; k – показатель адиабаты.

Если известны параметры в камере сгорания, то параметры в любом сечении сопла можно узнать по следующим соотношениям:

или ;

или ;

или ;

или .

В этих формулах – λ – приведенная скорость, отношение скорости газа в данном сечении сопла к скорости звука в критическом сечении, R – удельная газовая постоянная. Индексом «*» обозначены параметры торможения (в данном случае – параметры в камере сгорания).

Постановка задачи

1. Рассчитать параметры течения потока газов в сопле Лаваля: для этого профиль сопла Лаваля разбивается на 150 контрольных точек – . Разбиение осуществляем таким образом, чтобы минимальное сечение располагалось в точке . Определяются значения газодинамических функций давления, плотности и температуры в каждом сечении.

2. Расчёты выполнить средствами высокоуровневого свободно распространяемого языка программирования Python по следующей расчётной схеме и исходным данным:

Рисунок 1-Профиль сопла Лаваля

Таблица 1-Исходные данные

Приведенные исходные данные носят демонстрационный характер.

Расчёт сопла Лаваля средствами Python

Для продолжения решения задачи на Python, нужно связать λ – приведенную скорость газа с координатой x вдоль продольной оси. Для этого я воспользовался функцией fsolve из библиотеки SciPy со следующей инструкцией:

Привожу фрагмент программы для управления решателем с одной стартовой точкой:

Это единственно возможное на Python решение сложного алгебраического уравнения со степенной функцией от показателя адиабаты k. Например, даже для упрощённого уравнения с использованием библиотеки SymPy, получим недопустимое время расчёта только одной точки:

Время работы решателя: 195.675
0.16
1.95

Время работы программы: 0.222

Полученная эпюра распределения скоростей газового потока полностью соответствует изложенной выше теории. При этом, по предложенному алгоритму и библиотеке, время расчёта в 150 точках в 1000 раз меньше, чем для одной точки с использованием solve sympy.

Время работы программы: 0.203

Вывод

Время работы программы: 0.203

Вывод

Возникновение силы тяги от действия давления газа схематично показано на рисунке:

Время работы программы: 0.203

Вывод

Плотность газа на выходе из сопла уменьшается по приведенному в листинге уравнению газодинамики. Время выполнения программы приемлемое.

Источник