какую форму имеет сечение призмы плоскостью

Сечения призмы (справочный материал).

Справочный материал по теме «Сечение призмы».

Просмотр содержимого документа
«Сечения призмы (справочный материал).»

Определение 1. Сечением тела некоторой плоскостью α называют фигуру, состоящую из всех точек этого тела, лежащих в плоскости α.

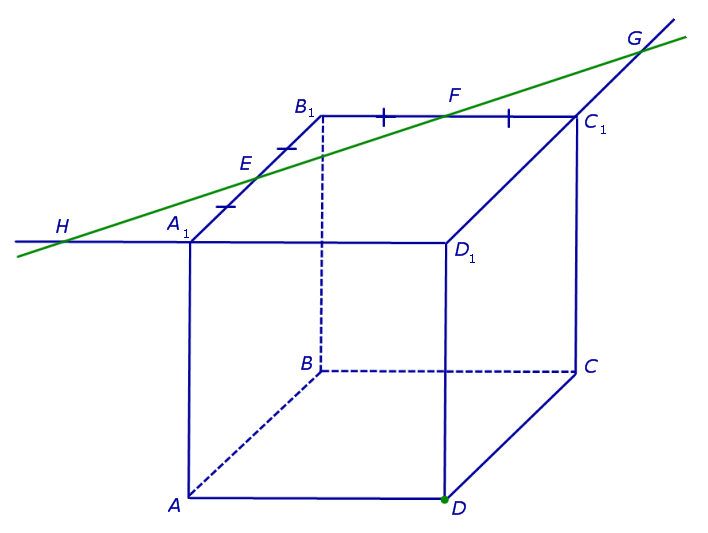
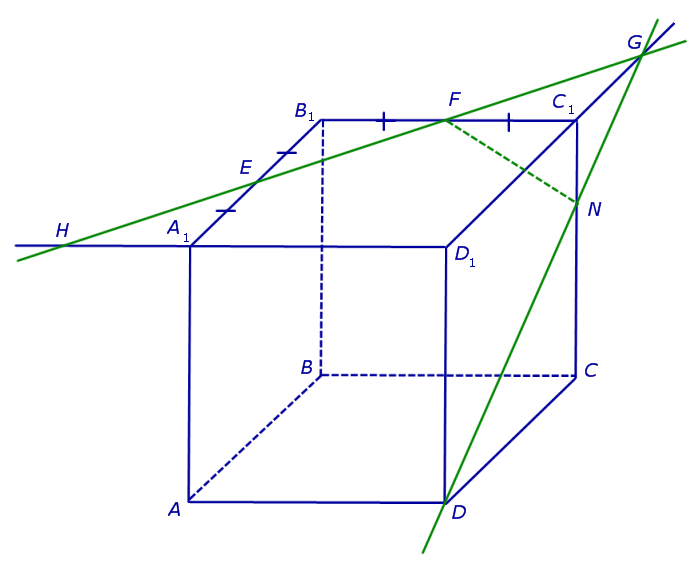
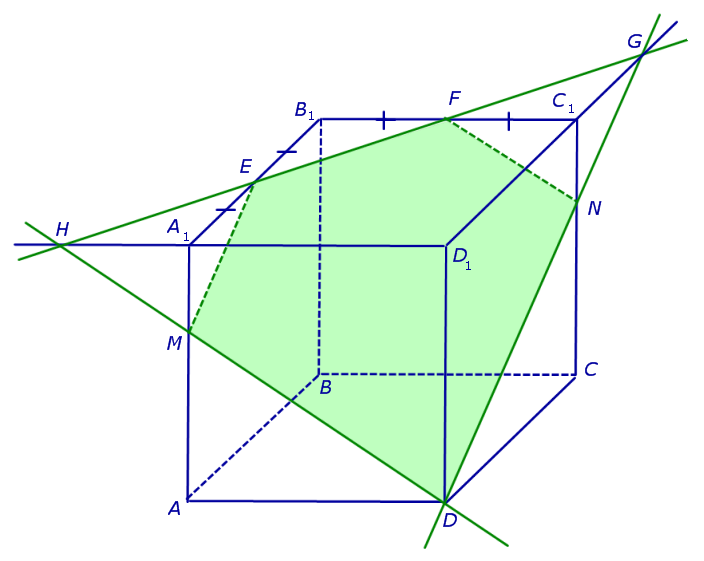
Точки G и D принадлежат плоскости сечения, а, значит, и вся прямая DG лежит в плоскости сечения. С другой стороны, эти точки лежат на ребрах (или их продолжениях) одной грани куба DD₁C₁C. Значит, точка пересечения DG с ребром куба C₁C (точка N ) будет принадлежать сечению. Таким образом, мы получаем еще два отрезка сечения: FN и DN (рис. 3).

Теперь, действуя аналогичным образом, проводим прямую HD, обозначаем точку перечения этой прямой с ребром AA₁ буквой M и проводим линии сечения ME и MD в плоскостях граней AA₁B₁B и AA₁D₁D (рис. 4).

В результате, как и показано на рисунке 4, получаем, что искомое сечение – пятиугольник DMEFN.

Предлагаем посетителю нашего сайта решить в качестве полезного упражнения следующую задачу.

Задача. Наши площадь сечения DMEFN, если ребро куба равно 6.

Перпендикулярные сечения призмы

Определение 2. Перпендикулярным сечением призмы называют такое сечение, плоскость которого пересекает все боковые ребра призмы и перпендикулярна к ним.

На рисунке 5 построено перпендикулярное сечение наклонной треугольной призмы – треугольник KLM. Хотим обратить Ваше внимание на то, что призма на рисунке 5 изображена лежащей на одной из своих боковых граней. Такой способ представления призмы на чертеже часто очень удобен при решении задач.

Источник

Что такое призма: определение, элементы, виды, варианты сечения

В данной публикации мы рассмотрим определение, основные элементы, виды и возможные варианты сечения призмы. Представленная информация сопровождается наглядными рисунками для лучшего восприятия.

Определение призмы

Призма – это геометрическая фигура в пространстве; многогранник с двумя параллельными и равными гранями (многоугольниками), а другие грани при этом являются параллелограммами.

На рисунке ниже представлен один из самых распространенных видов призмы – четырехугольная прямая (или параллелепипед). Другие разновидности фигуры рассмотрены в последнем разделе данной публикации.

Элементы призмы

Развёртка призмы – разложение всех граней фигуры в одной плоскости (чаще всего, одного из оснований). В качестве примера – для прямоугольной прямой призмы:

Примечание: свойства призмы представлены в отдельной публикации.

Варианты сечения призмы

Примечание: другие варианты сечения не так распространены, поэтому отдельно на них останавливаться не будем.

Виды призм

Рассмотрим разновидности фигуры с треугольным основанием.

Источник

Сечения призмы (11 класс)

Ищем педагогов в команду «Инфоурок»

Описание презентации по отдельным слайдам:

Сечения призмы Подготовил учитель математики, МБОУ СОШ №12, города Воронежа, Кузнецова Светлана Владимировна

Для решения многих геометрических задач, необходимо уметь строить сечения призмы различными плоскостями

Плоская фигура, образовавшаяся при пересечении какой-либо плоскости с пространственной фигурой, называется плоским сечением или просто сечением этой фигуры.

Сечением призмы является многоугольник, вершины которого расположены на ребрах, а стороны целиком лежат на гранях.

Вид сечения зависит от расположения плоскости

Сечения призмы плоскостями, параллельными боковым ребрам, являются параллелограммами В частности параллелограммами являются диагональные сечения. Это сечения плоскостями, проходящими через два боковых ребра, не принадлежащей одной грани.

Что значит построить сечение? Построить сечение призмы плоскостью – означает: В плоскости каждой пересекаемой грани многогранника указать 2-е точки, принадлежащие сечению; Соединить их прямой; Найти точки пересечения прямой с ребрами призмы.

Методы построения сечений призм Метод следов Метод внутреннего проектирования или метод вспомогательных сечений Комбинированный метод

Метод следов Если плоскость пересекает плоскость по прямой S, то прямую S называют следом плоскости на плоскость

Метод следов Метод следов включает три важных пункта: Строится линия пересечения (след) секущей плоскости с плоскостью основания многогранника. Находим точки пересечения секущей плоскости с ребрами многогранника. Строим и заштриховываем сечение.

Задача для самостоятельного решения. Призма ABCDA1B1C1D1. Построить сечение, проходящее через точки M, N, L.

Куда еще можно обратиться, чтобы узнать больше об этом вопросе. Адрес ссылки Краткое содержание http://www.freeware.ru/program_prog_id_1536.html Программа 3D SecBuilder строит сечение основных пространственных тел. «СТЕРЕОМЕТРИЯ. Электронный учебник-справочник» серия»Домашний компьютер и школа»

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Номер материала: ДВ-403713

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Власти Амурской области предложили продлить каникулы в школах в связи с эпидобстановкой

Время чтения: 2 минуты

В России запустили «Школу общественной дипломатии» для малочисленных народов

Время чтения: 2 минуты

Минобрнауки разрешило вузам перейти на дистанционное обучение

Время чтения: 1 минута

В школе в Пермском крае произошла стрельба

Время чтения: 1 минута

Минпросвещения планирует прекратить прием в колледжи по 43 профессиям

Время чтения: 1 минута

Школьников не планируют переводить на удаленку после каникул

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Геометрические фигуры. Призма. Объем призмы.

Призма — многогранник, 2 грани это конгруэнтные (равные) многоугольники, которые лежат в

параллельных плоскостях, а оставшиеся грани — параллелограммы, имеющие общие стороны с

этими многоугольниками. Либо (что тоже самое) — это многогранник, основаниями которого

являются равные многоугольники, а боковыми гранями — параллелограммы.

Призма является разновидностью цилиндра.

Элементы призмы.

конгруэнтными многоугольниками, которые лежат

в плоскостях, параллельных друг другу.

Боковые грани (ABLK, BCML, CDNM, DEPN, EAKP) – каждая

из граней, не считая оснований. Все боковые грани – это

Боковая поверхность – сумма боковых граней.

Полная поверхность – сумма основания и боковой

Боковые ребра (AK, BL, CM, DN, EP) – общие стороны

Высота (KR) – отрезок, который соединяет плоскости, в них лежат основания призмы. Он

перпендикулярен этим плоскостям.

Диагональ (BP) – отрезок, который соединяет 2 вершины призмы, которые не принадлежат одной

Диагональная плоскость – плоскость, которая проходит через боковое ребро призмы, а также

Диагональное сечение (EBLP) – пересечение призмы и диагональной плоскости. В сечении получается

Перпендикулярное (ортогональное) сечение – пересечение призмы и плоскости, перпендикулярной

боковому ребру призмы.

Свойства призмы.

где P — периметр перпендикулярного сечения, l — длина бокового ребра.

где P — периметр основания призмы, h — высота призмы.

Формула объема призмы:

Привальная четырехугольная пирамида.

Свойства правильной четырехугольной призмы.

Формулы для правильной четырехугольной призмы.

Виды призм.

Призма, у которой в основании лежит параллелограмм, является параллелепипедом.

Прямая призма — это призма, с перпендикулярными боковыми ребрами относительно плоскости основания.

Остальные призмы являются наклонными.

Правильная призма — прямая призма, в основании у нее лежит правильный многоугольник. Боковые

грани такой призмы — одинаковые прямоугольники.

Правильная призма, у которой боковые грани – квадраты (высота равна стороне основания), называется

полуправильным многогранником.

Источник

Справочный материал и задачи по теме «Призма»

Ищем педагогов в команду «Инфоурок»

Выбранный для просмотра документ Призма. Справочный материал и задачи.docx

Призма. Виды призмы

Если вы уже знакомы с призмой, и хотите для себя просто что-то уточнить, то вам вполне может хватить таблицы, что дана в конце статьи.

Мы же поведем подробный разговор.

Боковые грани – все грани, кроме оснований ( являются параллелограммами ).

Боковые ребра – общие стороны боковых граней ( параллельны между собой и равны ).

Диагональ – отрезок, соединяющий две вершины призмы, не принадлежащие одной грани.

Высота призмы – перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания.

Диагональная плоскость – плоскость, проходящая через боковое ребро призмы и диагональ основания.

Диагональное сечение –пересечение призмы и диагональной плоскости.

Перпендикулярное сечение – пересечение призмы и плоскости, перпендикулярной ее боковому ребру.

Различают призмы прямые (боковые ребра перпендикулярны плоскости основания) и наклонные (не прямые).

Среди прямых призм выделяют правильные.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник (равносторонний треугольник, квадрат, правильный шестиугольник и т.п.).

Параллелепипед – это призма, основаниями которой являются параллелограммы.

Среди параллелепипедов выделяют наклонные, прямые и прямоугольные параллелепипеды.

Прямой параллелепипед — это параллелепипед, у которого 4 боковые грани — прямоугольники.

Прямоугольный параллелепипед — это параллелепипед, у которого все грани — прямоугольники (или прямой параллелепипед с прямоугольником в основании).

Наклонный параллелепипед — это параллелепипед, боковые грани которого не перпендикулярны основаниям.

Частный случай прямоугольного параллелепипеда – куб.

Куб – прямоугольный параллелепипед, все грани которого – квадраты.

Далее – обещанная таблица, в которой собраны все основные виды призмы, с которыми приходится встречаться на ЕГЭ по математике

Вопросы для повторения:

— Что называется многогранником?

— Из каких частей состоит многогранник?

— Что называется гранью многогранника?

— Что называют диагональю многогранника?

Общие теоретические сведения

Призмой (n-угольной призмой) называется многогранник, составленный из двух равных многоугольников и , лежащих в параллельных плоскостях, и n параллелограммов .

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы

Основания призмы являются равными многоугольниками.

Боковые грани призмы являются параллелограммами.

Боковые ребра призмы параллельны и равны.

Различают призмы прямые,наклонныеи правильные. (слайд 6,7,8)

Диагональным сечением призмы называется ее сечение плоскостью, проходящей через два боковых ребра, которые не лежат в одной грани.

Если секущая плоскость пересекает все боковые ребра призмы и перпендикулярна им, то получающееся при этом сечение называется перпендикулярным сечением призмы.

Площадь боковой поверхности призмы равна сумме площадей ее боковых граней.

Площадь полной поверхности призмы равна сумме площадей оснований и площади боковой поверхности.

.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

.

Площадь боковой поверхности наклонной призмы равна произведению периметра перпендикулярного сечения на длину бокового ребра.

.

, где S – площадь основания, H – высота призмы.

Объем призмы можно найти, умножив площадь перпендикулярного сечения на длину бокового ребра. .

Частным случаем призмы является параллелепипед.

Параллелепипед– это призма, основаниями которой являются параллелограммы

Различают прямой, наклонный, прямоугольный параллелепипеды.

Длины непараллельных ребер прямоугольного параллелепипеда называют его линейными размерами (измерениями).

У прямоугольного параллелепипеда три измерения.

Объём прямоугольного параллелепипеда равен произведению трех его измерений.

Повтори необходимые формулы :

1. Прямоугольный параллелепипед

Пусть a, b, с – стороны, d – диагональ параллелепипеда,

S_n – полная поверхность.

d 2 = a 2 + b 2 + c 2

d=a

Ответь на теоретические вопросы по теме «Призма»

Ребро куба равно a. Найдите: диагональ грани, диагональ куба, периметр основания, площадь грани, площадь диагонального сечения; площадь поверхности куба; периметр и площадь сечения, проходящего через концы трёх рёбер, выходящих из одной и той же вершины. (слайд 14)

Существует ли призма, имеющая 50 рёбер? 54 ребра?

Решение: Число ребер n – угольной призмы 3n, поэтому призмы, имеющей 50 ребер, не существует, а 54 ребра имеет 18-угольная призма.

В правильной треугольной призме плоскость сечения BCА₁ образует с плоскостью основания двугранный угол φ. Постройте линейный угол этого двугранного угла. Дайте объяснение.

Построение: Проведём из вершины A правильного треугольника ABC высоту AK. Точка K принадлежит ребру BC. Соответственно, отрезок А₁К перпендикулярен ребру BC (по теореме о трёх перпендикулярах). Угол A₁КА– искомый.

1. Объем прямоугольного параллелепипеда равен 2. Чему будет равен объем параллелепипеда, если каждое его ребро увеличить в 3 раза.

Решение. Пусть ребра данного параллелепипеда равны a, b и c. Тогда имеем: V=abc=2. После увеличения каждого ребра в 3 раза его объём будет равен

V=3a*3b*3c =27 abc=27*2=54.

2. Аквариум имеет форму прямоугольного параллелепипеда высотой 30 см. Если в него налить 30 л. воды, то до верхнего края останется 5 см. Сколько литров воды нужно, чтобы наполнить пустой аквариум доверху?

Решение. Пусть V и H соответственно объем и высота параллелепипеда.

После заполнения пустого аквариума доверху H=30. Значит, 30*S=V.

Найдем отношение =, V=36 л.

3. Кубик весит 10 гр. Сколько граммов будет весить кубик, ребро которого в 3 раза больше, чем ребро первого кубика, если оба кубика изготовлены из одинакового материала.

Решение. Пусть V- объём данного параллелепипеда. После увеличения каждого ребра в 3 раза, его объём будет равен 27 V.

, x=270 гр.

В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AС₁ и плоскостью BСC₁.

Из точки А опускаем перпендикуляр.

Т.к. , , то и

Тогда AC₁ – наклонная, ВС₁– проекция прямой AC₁ на плоскость BСC₁. Т.к. угол между прямой и плоскостью – это угол между этой прямой и её проекцией на плоскость, то — искомый.

Треугольник ABC₁— прямоугольный.

.

Пусть сторона куба равна a. Тогда .

.

Ответ: .

2.Сторона основания правильной призмы ABCDA₁B₁C₁D₁ равна 12, а боковое ребро.Найдите градусную меру угла между плоскостями AB₁C и ABC.

Плоскость AB₁C пересекает плоскость ABC по прямой AC. Построим линейный угол двугранного угла между этими плоскостями.

Для этого из точки B проведём перпендикуляр к прямой AC. Т.к. призма правильная, то её основанием является правильный четырёхугольник – квадрат. Диагонали квадрата взаимно перпендикулярны, следовательно, искомый перпендикуляр-отрезок BO – половина диагонали BD, причём точка O – середина отрезка AC.

Следовательно, угол BOB₁ является линейным углом двугранного угла между плоскостями AB₁C и ABC.

В квадрате ABCD AB=12, BD=, BO=:2 =

Рассмотрим треугольник BB₁O.

, следовательно, .

3. В прямоугольном параллелепипеде АВСДА₁В₁С₁Д₁найдите угол между плоскостью АА₁С и прямой А₁В, если АА₁=3, АВ=4, ВС= 4.

Решение. Из точки В проведем перпендикуляр ВН к АС. А₁Н – проекция А₁В на плоскость АА₁С. Значит, угол ВА₁Н- искомый.

Из прямоугольного треугольника АВС находим ВН=2.

Из прямоугольного треугольника А₁АВ находим А₁В= 5.

Из прямоугольного треугольника А₁НВ находим sinА₁==

Ответ: arcsin.

Задачи для самостоятельного решения.

1. Объём прямоугольного параллелепипеда равен 32. Чему будет равен объём

параллелепипеда, если каждое его ребро уменьшить в 2 раза. (4)

2. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 36 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд той же формы, у которого сторона основания в 3 раза больше, чем у первого. Ответ выразите в сантиметрах. (4)

3. Закрытый сосуд в виде прямоугольного параллелепипеда с ребрами 30, 40 и 45 см. стоит на горизонтальной поверхности таким образом, что наименьшая грань является дном. В сосуд налили воду до уровня 36 см. На каком уровне окажется вода, если сосуд поставить на наибольшую грань? Ответ дайте в сантиметрах. ( 24 )

4. В кубе ABCDA₁B₁C₁D₁ найдите тангенс угла между прямой AA₁ и плоскостью BC₁D. ()

5. Основание прямой призмы АВСА₁В₁С₁— треугольник АВС, в котором, ВС=2, sinА=0,3. Высота призмы равна. Найдите синус угла между прямой ВС₁ и плоскостью АСС₁. ( 0,2)

6. В основании прямой призмы лежит равнобедренный треугольник с основанием, равным 6 см., и углом при вершине 120º. Диагональ боковой грани, содержащей основание равнобедренного треугольника, равна 10 см. Найдите площадь боковой поверхности. (48 +32)

Источник