какую форму имеет наша вселенная
Какова геометрия Вселенной?
Облачные решения хороши тем, что позволяют создавать проекты любой сложности, вплоть до виртуального дата-центра. Если попробовать визуализировать эти структуры, то получится этакая мини-вселенная. Давайте поиграем с геометрией, попробовав визуализировать разные модели нашей вселенной.
В нашем сознании вселенная кажется бесконечной. Но с помощью геометрии мы можем рассмотреть различные трехмерные формы, которые предлагают альтернативу «обычному» бесконечному пространству.
Когда смотришь на ночное небо, кажется, будто пространство расширяется во всех направлениях. Такова наша ментальная модель вселенной, но она не всегда является верной. В конце концов, было время, когда все думали, что Земля плоская, потому что изгибы нашей планеты было чрезвычайно трудно заметить, а уж про сферическую форму Земли и вовсе не думали.
Сегодня мы знаем, что Земля имеет форму сферы. Но мало кто задумывается о форме Вселенной. Подобно тому, как сфера стала альтернативой плоской Земле, другие трехмерные формы предлагают альтернативу «обычному» бесконечному пространству.
Мы можем задать два разных, но все же тесно связанных между собой вопросов о форме Вселенной. Один из них касается её геометрии: мелкозернистых локальных измерений таких элементов, как углы и области. Другой — о топологии: как эти локальные части сшиваются в общую форму.
Космологические данные свидетельствуют о том, что часть Вселенной, которую мы можем видеть, гладкая и однородная, по крайней мере приблизительно. Локальная ткань пространства выглядит одинаково в каждой точке и во всех направлениях. Только три геометрические формы подходят под это описание: плоская, сферическая и гиперболическая. Давайте рассмотрим эти модели, некоторые топологические предположения а также то, что говорят космологические данные о формах лучше всего описывающих нашу вселенную.
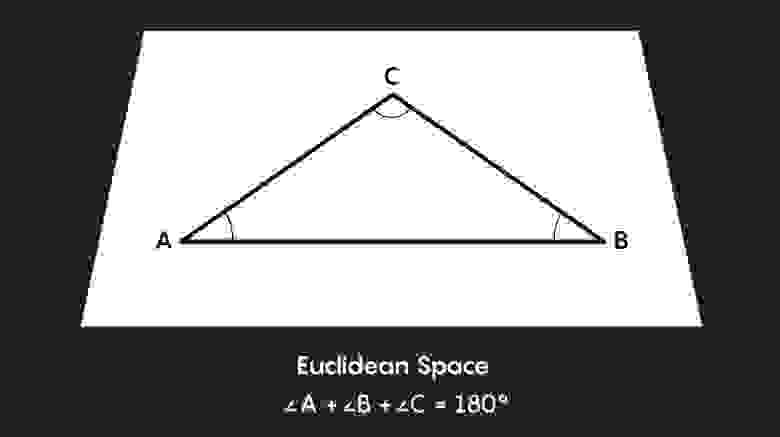
Плоская геометрия (планиметрия)
Это геометрия, которую мы изучали в школе. Углы треугольника составляют 180 градусов, а площадь круга — πr2. Самым простым примером плоской трёхмерной формы является обычное бесконечное пространство — то, что математики называют евклидовым пространством, — но есть и другие плоские формы, которые тоже нужно учитывать.
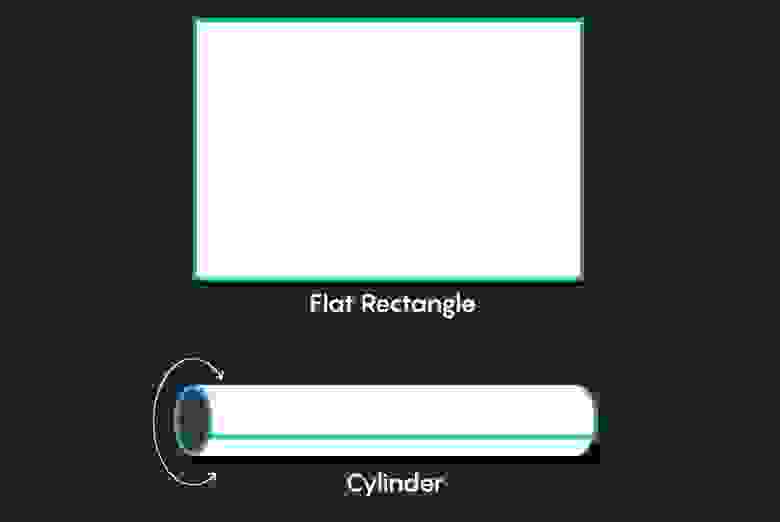
Эти формы сложнее визуализировать, но мы можем попробовать пофантазировать, думая в двух измерениях, а не в трёх. В дополнение к обычной евклидовой плоскости, мы можем создать другие плоские формы, вырезая часть плоскости и скрепляя её края вместе. Например, предположим, что мы вырезаем прямоугольный лист бумаги и скрепляем его противоположными краями. Склеивание верхней и нижней граней даёт нам цилиндр:
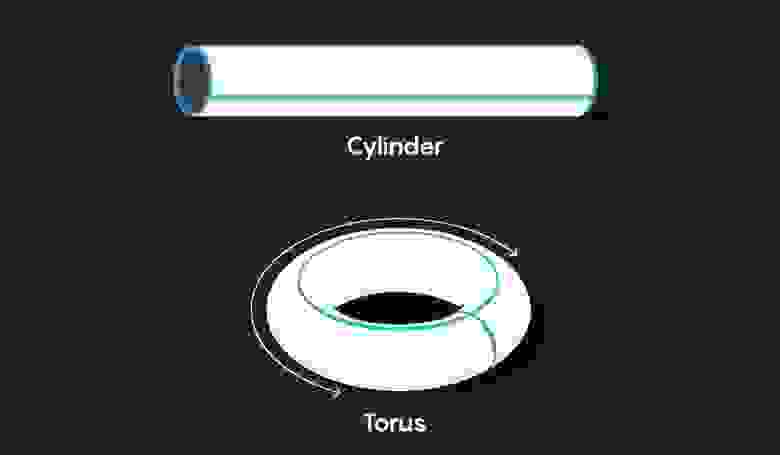
Потом мы можем заклеить правый и левый края, чтобы получить пончик (то, что математики называют тором):
Теперь вы, наверное, думаете: «но мне не кажется это плоским». И будете правы. Мы немного сжульничали, описывая, как устроен плоский тор. Если бы вы действительно попытались сделать тор из листа бумаги таким образом, вы бы столкнулись с определенными трудностями. Сделать цилиндр было бы легко, но заклеить концы цилиндра у вас бы не вышло: Бумага сминалась бы по внутреннему кругу тора и не растягивалась бы достаточно далеко по внешнему кругу. Вместо бумаги пришлось бы использовать какой-нибудь растягивающийся материал. Но это растяжение искажает длины и углы, меняя геометрию.
Внутри обычного трёхмерного пространства невозможно построить реальный, гладкий физический тор из плоского материала без искажения его геометрии. Но мы можем отвлечённо порассуждать о том, каково это — жить внутри плоского тора.
Представьте, что вы двумерное существо, чья вселенная — плоский тор. Поскольку геометрия этой вселенной происходит от плоского листа бумаги, все геометрические факты, к которым мы привыкли, такие же, только в маленьком масштабе: углы в треугольнике суммируются до 180 градусов и так далее. Но изменения, которые мы внесли в глобальную топологию путём вырезания и заклеивания, означают, что опыт пребывания в торе будет сильно отличаться от того, к чему мы привыкли.
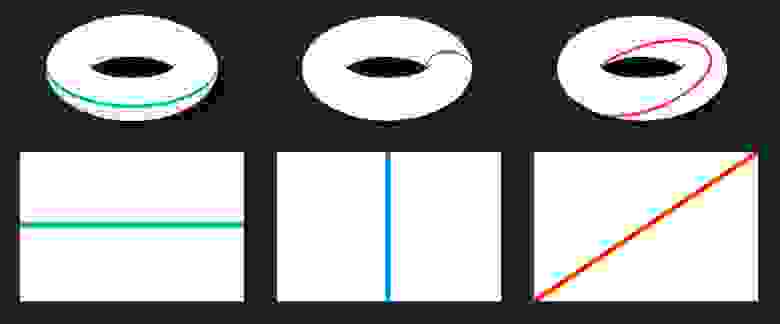
Для начала, на торе есть прямые пути, которые изгибаются и возвращаются туда, откуда начинались:
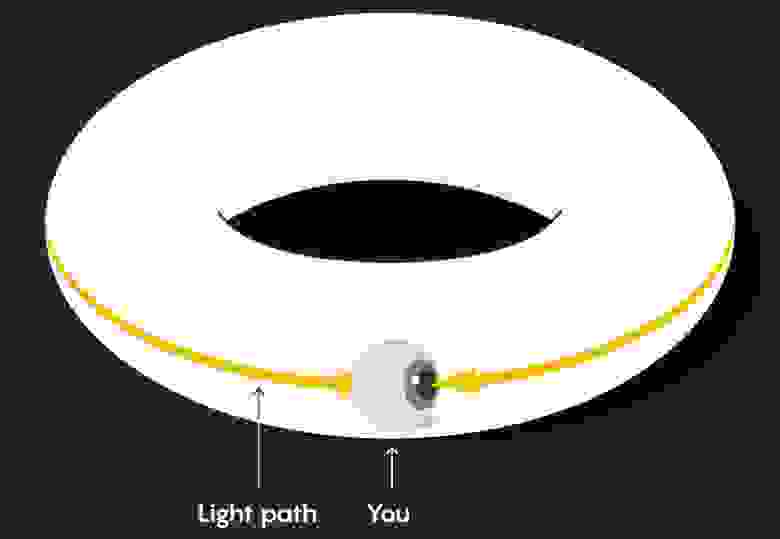
Эти пути выглядят изогнутыми на искаженном торе, но обитателям плоского тора они кажутся прямыми. А так как свет распространяется по прямым путям, то если посмотрите прямо, то увидите себя сзади:
На листе бумаги свет, который вы видите, проходил сзади, пока не достигал левого края, а затем снова появился справа, как будто в видеоигре:
Можно представить это иначе. Например, вы (или луч света) пересекаете одну из четырёх границ, появляясь в том, что кажется новой «комнатой». Но на самом деле это та же самая комната, только увиденная с новой перспективы.
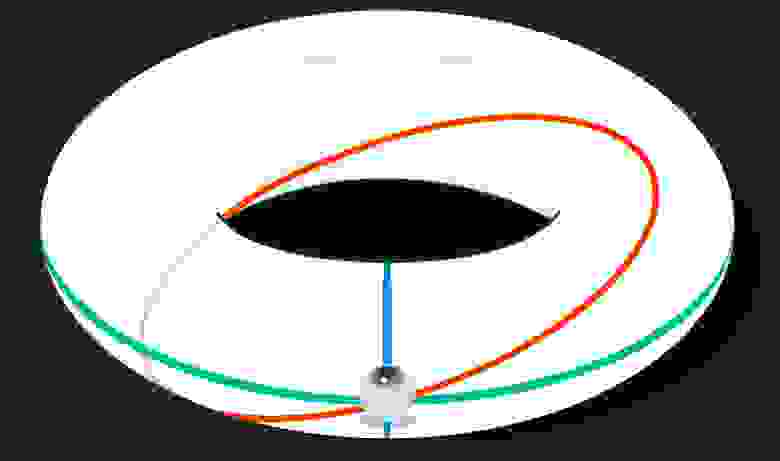
Это значит, что вы также можете видеть бесконечное множество различных копий себя, глядя в разных направлениях. Это своего рода эффект «Зеркального коридора», за исключением того, что копии вас не являются отражениями:
На пончике они соответствуют множеству различных колец, по которым свет может перемещаться от вас к вам:
Точно так же мы можем построить плоский трехмерный тор, приклеив противоположные стороны куба. Визуализировать это пространство как объект внутри обычного бесконечного пространства не получится, но мы можем абстрактно рассуждать о жизни внутри него.
Подобно тому, как жизнь в двухмерном торе была подобна жизни в бесконечном двухмерном массиве одинаковых прямоугольных комнат, жизнь в трёхмерном торе подобна жизни в бесконечном трёхмерном массиве одинаковых кубических комнат. Вы увидите бесконечно много копий себя:
Трёхмерный тор — всего лишь один из 10 различных плоских конечных миров. Существуют также плоские бесконечные миры, такие как трехмерный аналог бесконечного цилиндра. В каждом из этих миров существует разный набор зеркальных залов.
Является ли наша Вселенная одной из этих плоских форм?
Когда мы смотрим в космос, мы не видим бесконечно много копий себя. Тем не менее, на удивление трудно исключить эти плоские формы. Во-первых, они все имеют одну и ту же локальную геометрию, что и евклидово пространство, поэтому никакое локальное измерение не может различить их.
И если бы вы увидели копию себя, то это далёкое изображение показало бы, как вы (или ваша галактика, например) выглядели в далеком прошлом, так как свет должен был долго путешествовать, чтобы добраться до вас. Может быть, мы видим там неузнаваемые копии себя. Что ещё хуже, разные копии себя, как правило, находятся на разных расстояниях от вас, поэтому большинство из них будут выглядеть по-разному. И, возможно, они всё равно слишком далеко, чтобы мы могли их увидеть.
Чтобы обойти эти сложности, астрономы, как правило, ищут не копии самих себя, а повторяющиеся черты в самом дальнем из того, что мы можем видеть: космическое микроволновое фоновое (CMB) излучение, оставшееся после Большого взрыва. На практике это означает поиск пар кругов в реликтовом излучении, которые имеют совпадающие узоры горячих и холодных точек, что позволяет предположить, что это действительно один и тот же круг, который мы видим с двух разных точек.
В 2015 году астрономы провели именно такой анализ, используя данные с космического телескопа Планка. Они прочесали данные о видах совпадающих кругов, которые мы ожидали увидеть внутри плоского трехмерного тора или другой плоской трехмерной формы, называемой пластиной, но им не удалось их найти.
Это означает, что если мы действительно живем в торе, то он, вероятно, настолько велик, что любые повторяющиеся узоры лежат за пределами наблюдаемой вселенной.
Сферическая геометрия
Мы все знакомы с двумерными сферами — поверхностью шара, апельсина, Земли. Но что бы означало для нашей вселенной быть трёхмерной сферой?
Сложно представить себе трёхмерную сферу, но её легко описать с помощью простой аналогии. Подобно тому, как двумерная сфера — это совокупность всех точек на фиксированном расстоянии от некоторой центральной точки в обычном трёхмерном пространстве, так и трёхмерная сфера (или «трехсфера») — это совокупность всех точек на фиксированном расстоянии от некоторой центральной точки в четырёхмерном пространстве.
Жизнь в трёх сферах сильно отличается от жизни в плоском пространстве. Чтобы почувствовать это, представьте, что вы двухмерное существо, живущее в двухмерной сфере. Двухмерная сфера — это вся Вселенная — вы не можете видеть и не можете получить доступ ни к одному из окружающих трёхмерных пространств. Внутри этой сферической вселенной свет движется по кратчайшим путям: по большим кругам. Для вас эти большие круги кажутся прямыми линиями.
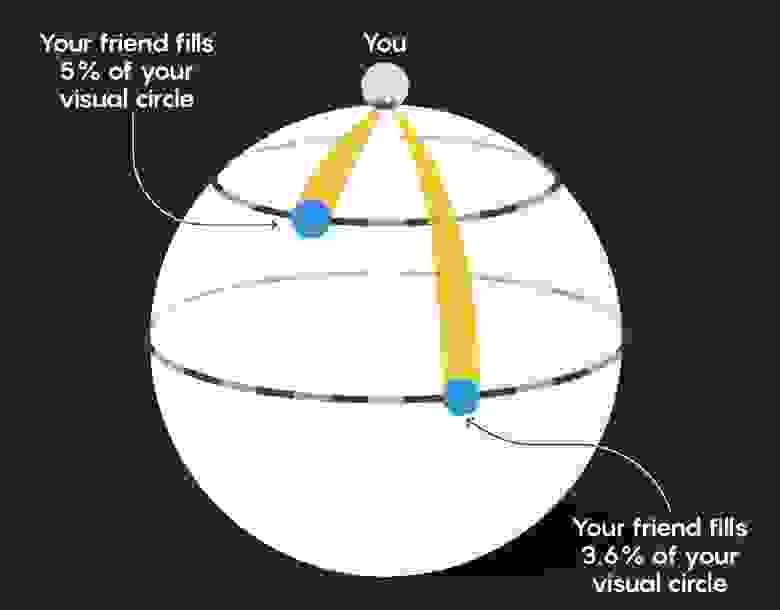
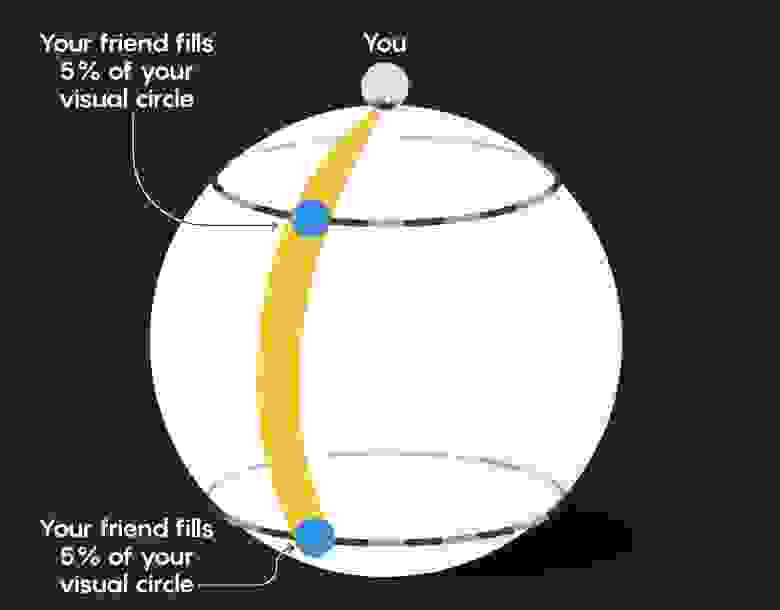
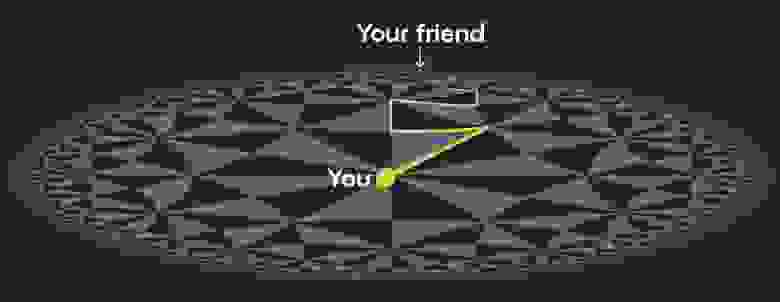
Теперь представьте, что вы и ваш двумерный друг тусуетесь на Северном полюсе, и ваш друг идет на прогулку. В то время как ваш друг прогуливается, вначале он будет становиться все меньше и меньше в вашем зрительном пространстве, так же, как и в нашем обычном мире (хотя он не будет уменьшаться так быстро, как мы привыкли). Это из-за того, что пока ваше зрительное пространство будет увеличиваться, ваш друг будет занимать все меньше и меньше места в нём:
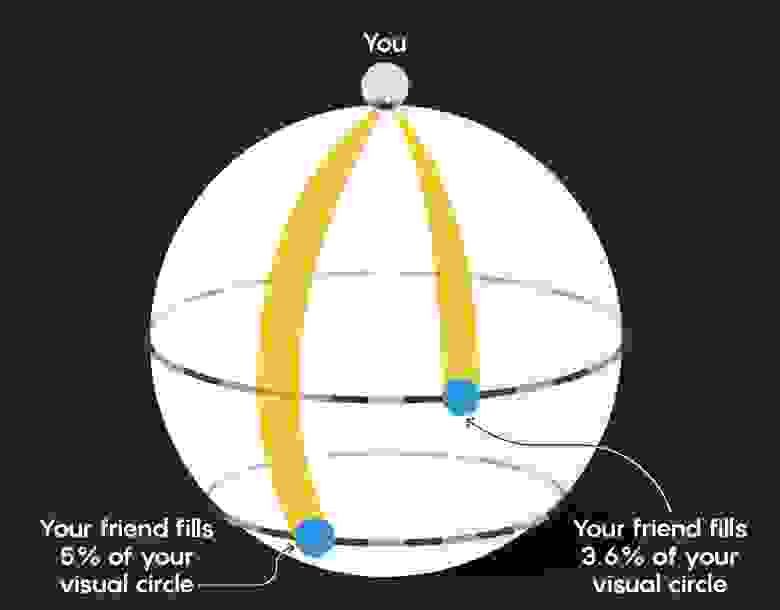
Но как только друг проходит экватор, происходит что-то странное: он начинает казаться всё больше и больше, чем дальше уходит. Это потому, что процент, который он занимает в вашем зрительном пространстве, растёт:
Когда ваш друг будет в трёх метрах от Южного полюса, он будет выглядеть такими же большими, как и в трёх метрах от вас:
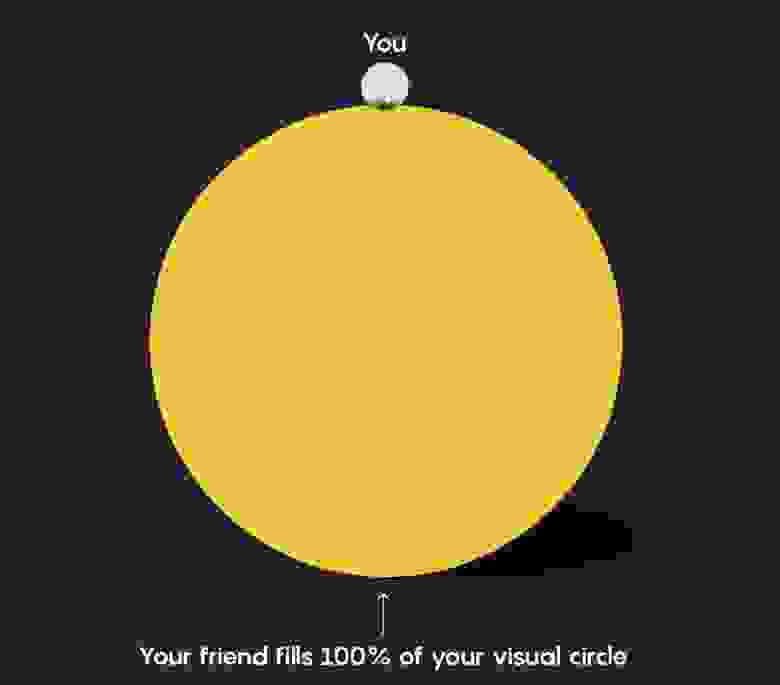
А когда он достигнет самого Южного полюса, его можно будет увидеть во всех направлениях, так что он заполнит весь ваш визуальный горизонт:
Если на Южном полюсе никого нет, то ваш визуальный горизонт — это нечто ещё более странное: вы сами. Всё потому, что свет, исходящий от вас, будет идти по всей сфере, пока не вернется к вам.
Это можно соотнести с жизнью в трёхмерной сфере. Каждая точка на трёхсфере имеет противоположную точку, и, если там есть объект, мы увидим его как фон, будто это небо. Если же там ничего нет, то вместо этого мы увидим самих себя в качестве фона – будто наш экстерьер был наложен на воздушный шар, затем вывернут наизнанку и надут, чтобы стать целым горизонтом.
Трёхсфера является фундаментальной моделью сферической геометрии, но это не единственное такое пространство. Подобно тому, как мы строили плоские пространства, вырезая кусок из евклидового пространства и склеивая его, мы можем строить сферические пространства, склеивая подходящий кусок из трех сфер. Каждая из этих склеенных форм, как и в торе, будет иметь эффект «лабиринта отражений», но в этих сферических формах есть только ограниченное количество комнат, через которые можно пройти.
Может ли наша Вселенная быть сферической?
Даже самые самовлюбленные люди не могут представить себя фоном всего ночного неба. Но, как и в случае с плоским тором, тот факт, что мы не видим какое-либо явление, не означает, что оно не может существовать. Окружность сферической вселенной может быть больше, чем размер обозримой вселенной, что делает фон слишком далёким, чтобы его можно было разглядеть.
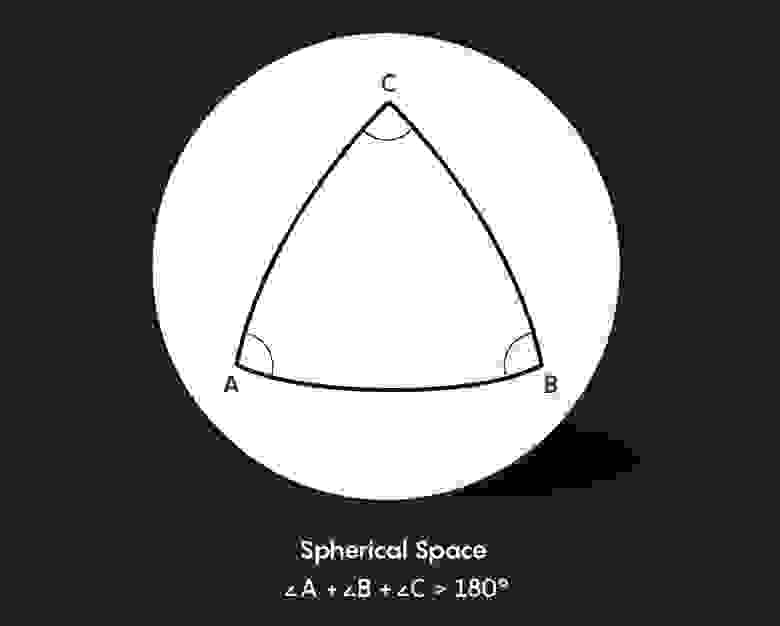
Но в отличие от тора, сферическая вселенная может быть обнаружена с помощью чисто локальных измерений. Сферические формы отличаются от бесконечного евклидового пространства не только глобальностью топологии, но и тончайшей геометрией. Например, из-за того, что прямые линии в сферической геометрии представляют собой большие окружности, треугольники получаются более пухлые, чем их евклидовые аналоги, а сумма углов больше 180 градусов:
В сущности, измерение космических треугольников является основным способом, с помощью которого космологи проверяют, является ли Вселенная изогнутой. Для каждой горячей или холодной точки на космическом микроволновом фоне известны ее диаметр по горизонтали и расстояние от Земли, что образует три стороны треугольника. Мы можем измерить угол, под которым пятно скрывается в ночном небе — один из трёх углов треугольника. Затем проверить, подходит ли для плоской, сферической или гиперболической геометрии (в которой сумма углов треугольника больше 180 градусов) комбинация из длины сторон и измеренного угла.
Большинство таких исследований, наряду с другими измерениями кривизны, свидетельствуют о том, что Вселенная либо плоская, либо очень близка к плоской. Но одна исследовательская группа недавно заявила, что часть данных, полученных с помощью космического телескопа Планка в 2018 году, свидетельствуют о существовании сферической вселенной. Другие исследователи возражают против этого утверждения, полагая, что это скорее всего, статистическая случайность.
Гиперболическая геометрия
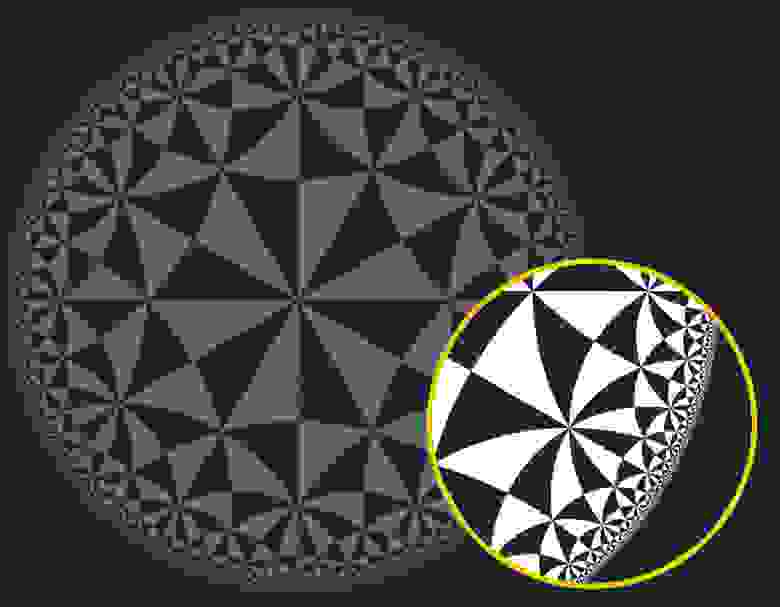
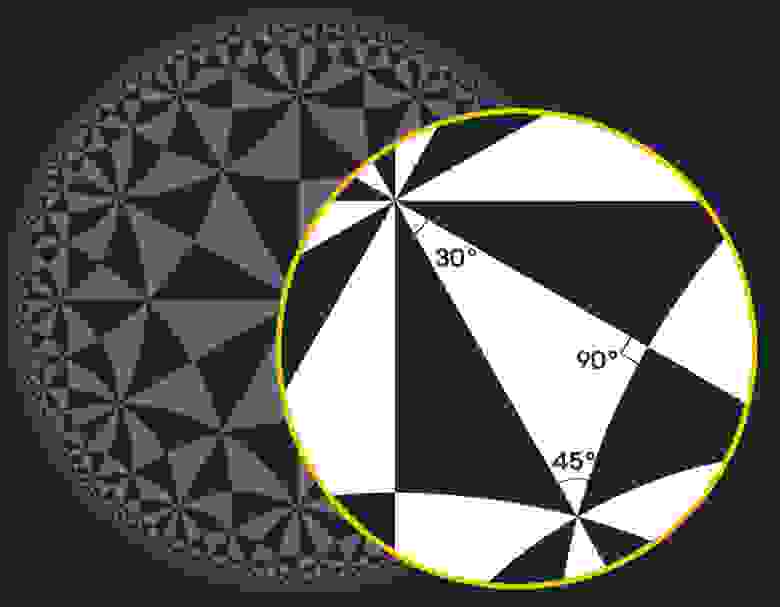
В отличие от сферы, которая изгибается сама по себе, гиперболическая геометрия раскрывается вовне. Это геометрия гибких шляп, коралловых рифов и седел. Базовая модель гиперболической геометрии – это бесконечное пространство, подобно плоскому евклидовому пространству. Но поскольку гиперболическая геометрия распространяется наружу намного быстрее, чем плоская, не существует способа поместить даже двумерную гиперболическую плоскость внутри обычного евклидового пространства, если только мы не хотим исказить его геометрию. Здесь, например, искажено представление о гиперболической плоскости, известной как диск Пуанкаре:
С нашей точки зрения, треугольники вблизи пограничного круга выглядят намного меньше, чем вблизи центра, но с точки зрения гиперболической геометрии все треугольники одинакового размера. Если бы мы попытались сделать треугольники одинакового размера – например, используя растягивающийся материал для нашего диска и увеличивая каждый треугольник по очереди, выходя наружу из центра, — наш диск стал бы похож на гибкую шляпу и сгибался бы все больше и больше по мере того, как мы прокладывали себе путь наружу. По мере приближения к границе, этот изгиб становился бы все более неконтролируемым.
С точки зрения гиперболической геометрии, граничная окружность бесконечно далека от любой внутренней точки, так как для этого нужно пересечь бесконечно много треугольников. Таким образом, гиперболическая плоскость простирается до бесконечности во всех направлениях, точно так же, как и евклидовая плоскость. Но с точки зрения локальной геометрии жизнь в гиперболической плоскости сильно отличается от того, к чему мы привыкли.
В простой евклидовой геометрии окружность прямо пропорциональна её радиусу, но в гиперболической геометрии окружность растет экспоненциально по сравнению с радиусом. Мы можем видеть экспоненциальное скопление в массах треугольников вблизи границы гиперболического диска.
Из-за этой особенности математики любят говорить, что в гиперболическом пространстве легко заблудиться. Если ваш друг уйдёт от вас в обычном евклидовом пространстве, он начнёт выглядеть меньше, но это будет происходить медленно, потому что ваш визуальный круг растёт не так стремительно. В гиперболическом пространстве ваш зрительный круг растёт в геометрической прогрессии, так что вскоре ваш друг будет выглядеть сжатым до экспоненциально мелкой точки. Если вы внимательно не отследили его маршрут, найти дорогу к нему будет практически невозможно.
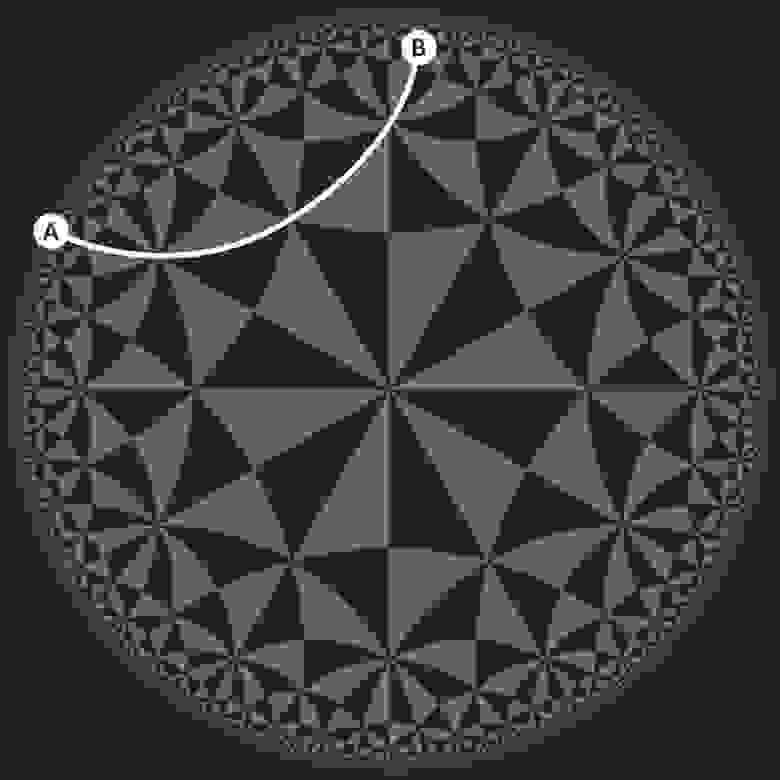
А в гиперболической геометрии сумма углов треугольника составляет менее 180 градусов — например, треугольники в нашей плитке диска Пуанкаре имеют углы, составляющие 165 градусов:
Боковые стороны этих треугольников не выглядят прямыми, но это только потому, что мы смотрим на гиперболическую геометрию через искаженную линзу. Для жителя диска Пуанкаре эти кривые являются прямыми линиями, потому что самый быстрый способ добраться из точки A в точку B – срезать путь к центру:
Есть вполне закономерный способ изготовления трехмерного аналога диска Пуанкаре – просто сделайте трехмерный шар и заполните его трехмерными формами, которые становятся меньше по мере приближения к граничной зоне, как треугольники в диске Пуанкаре. И точно так же, как в плоской и сферической геометрии, мы можем сделать ряд других трехмерных гиперболических пространств, вырезая подходящий кусок трехмерного гиперболического шарика и склеивая его грани.
Может ли наша Вселенная быть гиперболической?
Гиперболическая геометрия, с ее узкими треугольниками и экспоненциально растущими кругами, не похожа на геометрию пространства вокруг нас. И действительно, как мы уже видели, большинство космологических измерений указывают на плоскую вселенную.
Но при этом возможность того, что мы живем либо в сферическом, либо в гиперболическом мире, не исключена, так как маленькие кусочки обоих этих миров выглядят почти плоскими. Например, малые треугольники в сферической геометрии имеют углы, которые составляют лишь чуть более 180 градусов, а малые треугольники в гиперболической геометрии имеют углы, которые составляют лишь чуть менее 180 градусов.
Неспроста древние люди считали, что Земля плоская – кривизна Земли была слишком мала, чтобы ее можно было обнаружить. Чем больше сферическая или гиперболическая форма, тем более плоская каждая маленькая деталь. Поэтому, если наша Вселенная имеет чрезвычайно большую сферическую или гиперболическую форму, то та часть, которую мы можем наблюдать, может быть настолько близка к плоской, что ее кривизна может быть обнаружена только с помощью сверхточных приборов, которые нам ещё только предстоит изобрести.
Что ещё полезного можно почитать в блоге Cloud4Y
Подписывайтесь на наш Telegram-канал, чтобы не пропустить очередную статью. Пишем не чаще двух раз в неделю и только по делу.
Какую форму имеет наша вселенная
Доктор физико-математических наук А. МАДЕРА.
В древности люди полагали, что живут на обширной плоской поверхности, хотя и покрытой кое-где горами и впадинами. Это убеждение сохранялось на протяжении многих тысяч лет, пока Аристотель в IV веке до н. э. не заметил, что уходящее в море судно пропадает из виду не потому, что по мере удаления уменьшается до недоступных глазу размеров. Напротив, сначала исчезает корпус корабля, потом паруса и, наконец, мачты. Это привело его к заключению, что Земля должна быть круглой.
За прошедшие тысячелетия сделано множество открытий, накоплен колоссальный опыт. И тем не менее до сих пор остаются без ответа фундаментальные вопросы: конечна или бесконечна Вселенная, внутри которой мы обитаем, и какова ее форма?
Последние наблюдения астрономов и исследования математиков показывают, что форму нашей Вселенной следует искать среди восемнадцати так называемых трехмерных ориентируемых евклидовых многообразий, причем претендовать на нее могут только десять.
Любые умозаключения о возможной форме нашей Вселенной должны опираться на реальные факты, полученные из астрономических наблюдений. Без этого даже самые красивые и правдоподобные гипотезы обречены на неудачу. Поэтому посмотрим, что говорят о Вселенной результаты наблюдений.
Прежде всего, заметим, что, в каком бы месте Вселенной мы ни находились, вокруг любой ее точки можно очертить сферу произвольного размера, содержащую внутри пространство Вселенной. Такое несколько искусственное построение говорит космологам, что пространство Вселенной представляет собой трехмерное многообразие (3-многообразие).
Согласно принятой на сегодняшний день концепции, примерно через 300 тысяч лет после Большого взрыва температура Вселенной упала до уровня, достаточного для объединения электронов и протонов в первые атомы (см. «Наука и жизнь» №№ 11, 12, 1996 г.). Когда это произошло, излучение, которое вначале рассеивалось заряженными частицами, внезапно получило возможность беспрепятственно проходить через расширяющуюся Вселенную. Это известное ныне как космическое микроволновое фоновое, или реликтовое, излучение удивительно однородно и обнаруживает только очень слабые отклонения (флуктуации) интенсивности от среднего значения (см. «Наука и жизнь» № 12, 1993 г.). Такая однородность может быть только во Вселенной, кривизна которой всюду постоянна.
Постоянство кривизны означает, что пространство Вселенной имеет одну из трех возможных геометрий: плоскую евклидову сферическую с положительной кривизной или гиперболическую с отрицательной. Эти геометрии обладают совершенно разными свойствами. Так, например, в евклидовой геометрии сумма углов треугольника равна точно 180 градусам. В сферической и гиперболической геометриях это не так. Если на сфере взять три точки и провести между ними прямые, то сумма углов между ними составит больше 180 градусов (вплоть до 360). В гиперболической же геометрии эта сумма меньше 180 градусов. Имеются и другие кардинальные отличия.
Так какую же геометрию для нашей Вселенной выбрать: евклидову, сферическую или гиперболическую?
Итак, в малых (по астрономическим меркам) масштабах Вселенная предстает как евклидова (хотя, конечно, экстраполировать выводы Гаусса на всю Вселенную нельзя).
Еще в тридцатых годах XX столетия математики доказали, что существует только 18 различных евклидовых трехмерных многообразий и, следовательно, только 18 возможных форм Вселенной вместо их бесконечного числа. Понимание свойств этих многообразий помогает экспериментально определить истинную форму Вселенной, так как целенаправленный поиск всегда эффективнее поиска вслепую.
Маловероятно, что мы живем в таком мире. Космологи полагают, что если бы наша Вселенная была неориентируемой, то происходило бы излучение энергии из пограничных зон, в которых взаимодействуют материя и антиматерия. Однако ничего подобного никогда не наблюдалось, хотя теоретически и можно предположить, что подобные зоны существуют за пределами области Вселенной, доступной нашему взгляду. Поэтому резонно исключить из рассмотрения восемь неориентируемых многообразий и ограничить возможные формы нашей Вселенной десятью ориентируемыми евклидовыми трехмерными многообразиями.
ВОЗМОЖНЫЕ ФОРМЫ ВСЕЛЕННОЙ
Существует множество поверхностей, которые топологически отличны от тора и сферы. Например, добавив к тору ручку, подобную той, что мы видим у чашки, мы получим новую дырку, а значит, и новую фигуру. Тор с ручкой будет гомеоморфен фигуре, напоминающей крендель, которая в свою очередь гомеоморфна сфере с двумя ручками. Добавление каждой новой ручки создает еще одну дырку, а значит, и другую поверхность. Таким способом можно получать бесконечное их количество.
Все такие поверхности называются двухмерными многообразиями или просто 2-многообразиями. Это означает, что вокруг любой их точки можно очертить окружность произвольного радиуса. На поверхности Земли можно нарисовать круг, содержащий ее точки. Если мы видим только такую картину, резонно считать, что она представляет собой бесконечную плоскость, сферу, тор или вообще любую другую поверхность из бесконечного числа торов или сфер с различным числом ручек.
Эти топологические формы могут быть довольно сложны для понимания. И чтобы легче и отчетливее представи ть их себе, склеим цилиндр из квадратного листа бумаги, соединив его левую и правую стороны. Квадрат в этом случае называется фундаментальной областью для тора. Если теперь мысленно склеить основания цилиндра (материал цилиндра эластичен), получится тор.
Неразличимость внутренних геометрий для самых разных поверхностей связана с важной их топологической характеристикой, называемой развертываемостью. Так, поверхности цилиндра и конуса выглядят совершенно различными, но тем не менее их геометрии абсолютно одинаковы. Обе они могут быть развернуты в плоскости без изменения длин отрезков и углов между ними, поэтому для них справедлива евклидова геометрия. Это же относится и к тору, поскольку он представляет собой поверхность, развертывающуюся в квадрат. Такие поверхности называют изометричными.
Бесчисленное число торов можно сформировать и из других плоских фигур, например из различных параллелограммов или шестиугольников, склеивая их противоположные края. Однако для этого годится далеко не каждый четырехугольник: длины его склеенных сторон должны быть одинаковы ми. Такое требование необходимо, чтобы избежать при склейке удлинений или сжиманий краев области, которые нарушают евклидову геометрию поверхности.
Теперь перейдем к многообразиям большей размерности.
ПРЕДСТАВЛЕНИЕ ВОЗМОЖНЫХ ФОРМ ВСЕЛЕННОЙ
Попробуем представить себе возможные формы нашей Вселенной, которые, как мы уже видели, надо искать среди десяти ориентируемых евклидовых трехмерных многообразий.
Для представления евклидова 3-многообразия применим использованный выше метод для двухмерных многообразий. Там мы использовали в качестве фундаментальной области тора квадрат, а для представления трехмерного многообразия станем брать трехмерные объекты.
Возьмем вместо квадрата куб и подобно тому, как мы склеивали противоположные края квадрата, склеим вместе противоположные грани куба во всех их точках.
Важно отметить круговую природу этого и многих других многообразий. Если бы Вселенная действительно имела такую форму, то, покинув Землю и летя без каких-либо изменений курса, мы в конце концов вернулись бы домой. Нечто подобное наблюдается и на Земле: двигаясь на запад вдоль экватора, мы рано или поздно вернемся в исходную точку с востока.
Трехмерные торы могут быть получены не только с помощью куба. Подобно тому как параллелограмм образует 2-тор, склеивая противоположные грани параллелепипеда (трехмерного тела, ограниченного параллелограммами), мы создадим 3-тор. Из разных параллелепипедов образуются пространства с различными замкнутыми путями и углами между ними.
Эти и все другие конечные многообразия очень просто включаются в картину расширяющейся Вселенной. Если фундаментальная область многообразия постоянно расширяется, образованное ею пространство будет расширяться тоже. Каждая точка в расширяющемся пространстве все дальше отдаляется от остальных, что в точности соответствует космологической модели. При этом, однако, нужно принять во внимание, что точки вблизи одной грани всегда будут соседствовать с точками на противоположной грани, поскольку, вне зависимости от размера фундаментальной области, противоположные грани склеены.
На этом заканчивается список конечных ориентируемых евклидовых трехмерных, так называемых компактных многообразий. Вполне вероятно, что среди них и нужно искать форму нашей Вселенной.
Многие космологи полагают, что Вселенная конечна: трудно представить себе физический механизм возникновения бесконечной Вселенной. Тем не менее рассмотрим четыре оставшихся ориентируемых некомпактных евклидовых трехмерных многообразия, пока не получены реальные данные, исключающие их существование.
Повернув на 180 градусов одну из склеиваемых поверхностей трубчатого пространства, получим повернутое трубчатое пространство. Этот поворот с учетом бесконечной длины трубки придает ему необычные характеристики. Например, две точки, расположенные очень далеко одна от другой, по разным концам фундаментальной области, после склейки окажутся рядом.
Какова же все-таки форма нашей Вселенной?
Чтобы из приведенных выше десяти евклидовых 3-многообразий выбрать одно в качестве формы нашей Вселенной, необходимы дополнительные данные астрономических наблюдений.
Свет распространяется с конечной скоростью, поэтому, наблюдая Вселенную, мы, в сущности, смотрим в прошлое. Даже если мы однажды обнаружим изображение нашей Галактики, то не сможем узнать ее, потому что в свои «молодые годы» она выглядела совершенно иначе. Слишком сложно из огромного количества галактик узнать копию нашей.
В трехмерной Вселенной мы наблюдаем небо по всем направлениям, то есть в пределах сферы. Двухмерные жители двухмерной Вселенной смогли бы наблюдать его только в пределах круга. Если бы этот круг был меньше фундаментальной области их Вселенной, они не могли бы получить никаких указаний о ее форме. Если, однако, круг видения двухмерных созданий больше фундаментальной области, они смогли бы увидеть пересечения и даже повторение образов Вселенной и попытаться найти точки с одинаковыми температурами, которые соответствуют одной и той же ее области. Если в их круге видения оказалось бы достаточно много таких точек, они смогли бы заключить, что живут в торовой Вселенной.
Несмотря на то, что мы живем в трехмерной Вселенной и видим сферическую область, перед нами встает та же проблема, что и перед двухмерными созданиями. Если наша сфера видения меньше фундаментальной области Вселенной 300 000-летней давности, мы ничего необычного не увидим. В противном случае сфера будет пересекать ее по кругам. Обнаружив два круга, имеющих одинаковые вариации микроволнового излучения, космологи смогут сравнить их ориентацию. Если круги расположены крест-накрест, это будет означать наличие склейки, но без поворота. Некоторые из них, однако, могут сочетаться в соответствии с поворотом на четверть или на половину. Если этих кругов удастся обнаружить достаточно много, тайна фундаментальной области Вселенной и ее склейки будет раскрыта.
Однако до тех пор, пока не появится точная карта микроволнового излучения, космологи никаких заключений сделать не смогут. В 1989 году исследователи из НАСА попытались создать карту реликтового излучения космического пространства. Однако угловое разрешение спутника составляло порядка 10 градусов, что не позволило сделать точные измерения, удовлетворяющие космологов. Весной 2002 года НАСА предприняло вторую попытку и запустило зонд, который нанес на карту температурные флуктуации с угловым разрешением уже порядка 0,2 градуса. В 2007 году Европейское космическое агентство планирует использовать спутник «Планк», имеющий угловое разрешение 5 дуговых секунд.
По материалам журналов «American Scientist» и «Popular Science».