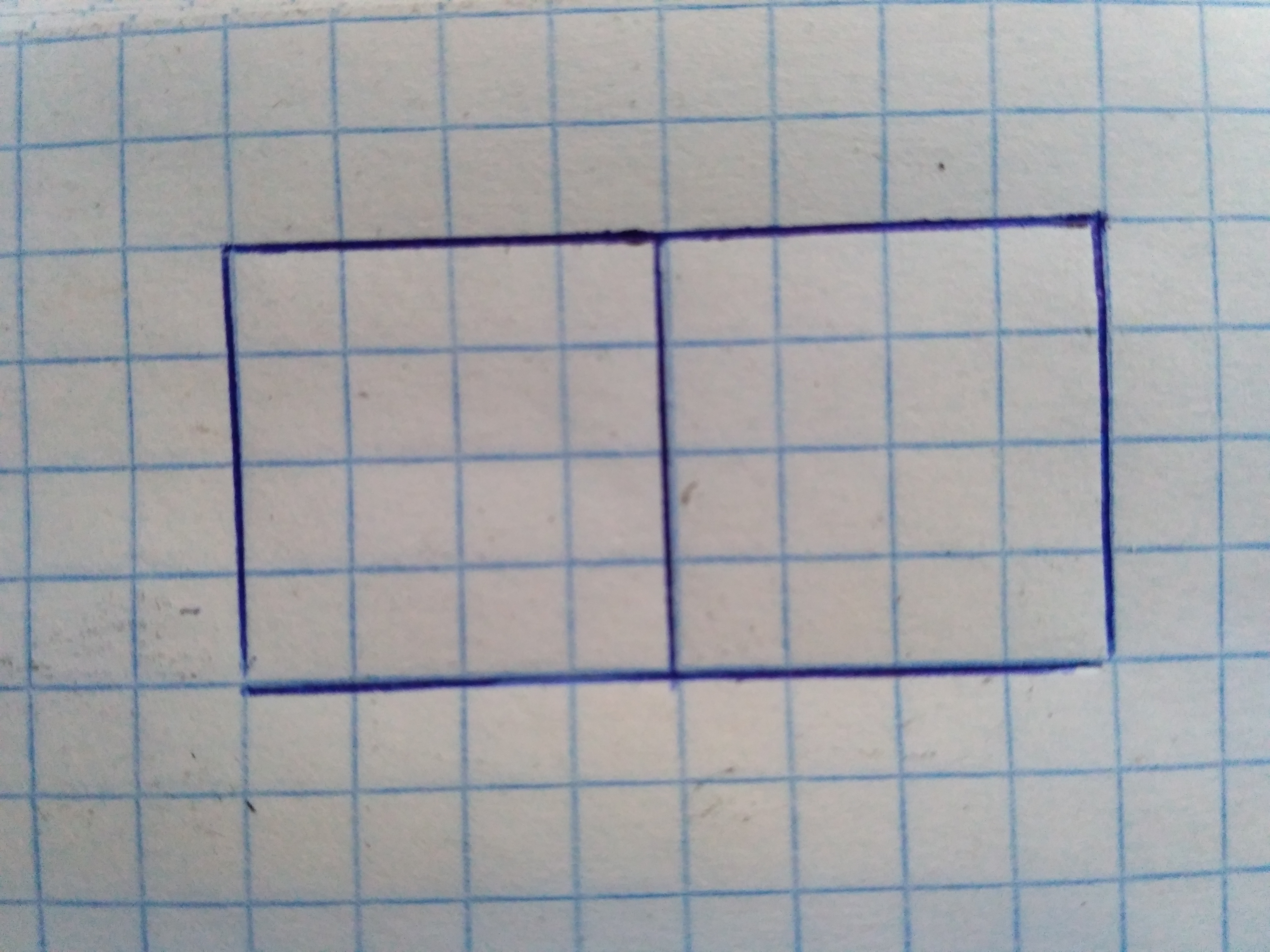
какую часть прямоугольника составляет каждый квадрат
Проведи отрезок так чтобу получилось 2 квадрата какую часть прямоугольника составляет каждый квадрат?
Проведи отрезок так чтобу получилось 2 квадрата какую часть прямоугольника составляет каждый квадрат.
Каждый квадрат составляет 1 / 2 от всего прямоугольника.
< ; p> ; От прямоугольника отрезали квадрат со стороной, равной меньшей стороне прямоугольника?
< ; p> ; От прямоугольника отрезали квадрат со стороной, равной меньшей стороне прямоугольника.
От оставшейся части прямоугольника снова отрезали квадрат со стороной, равной меньшей стороне получившегося прямоугольника.
И наконец в третий раз от оставшейся части прямоугольника отрезали квадрат со стороной равной меньшей стороне прямоугольника, получившегося после второго разрезания.
После того остался квадрат со стороной 1 см.
Какие размеры имел первоночальный прямоугольник?
Начетили квадрат его разделили на 4 равных квадрата?
Начетили квадрат его разделили на 4 равных квадрата.
Затем каждую часть разделили еще на 4 равных квадратов.
Какую часть большего квадрата составляет один маленький квадрат.
В квадрате проведи два отрезка так, чтобы получилось два треугольника и три прямоугольника?
В квадрате проведи два отрезка так, чтобы получилось два треугольника и три прямоугольника.
Внутри квадрата проведи 2 линии чтоби получилось 5 квадратов?
Внутри квадрата проведи 2 линии чтоби получилось 5 квадратов.
Проведи В прямоугольнике ABCD один отрезок так чтобы получилось 3 прямоугольника?
Проведи В прямоугольнике ABCD один отрезок так чтобы получилось 3 прямоугольника.
Квадрат сторона которого равна 6 сантиметров разбит на четыре части прямоугольника рисунок б какую часть площади квадрата составляет площадь каждого из прямоугольников номер б?
Квадрат сторона которого равна 6 сантиметров разбит на четыре части прямоугольника рисунок б какую часть площади квадрата составляет площадь каждого из прямоугольников номер б.
Начерти в тетради такой прямоугольник Проведи в этом прямоугольнике один отрезок так чтобы получился квадрат Найди периметр каждого из получившихся прямоугольников?
Начерти в тетради такой прямоугольник Проведи в этом прямоугольнике один отрезок так чтобы получился квадрат Найди периметр каждого из получившихся прямоугольников.
НАЧЕРТИ В ТЕТРАДИ такой прямоугольник?
НАЧЕРТИ В ТЕТРАДИ такой прямоугольник.
Проведи в этом прямоугольнике один отрезок так, чтобы получился квадрат найди периметр каждого из получившийся прямоугольников.
Черти в тетради такой прямоугольник?
Черти в тетради такой прямоугольник.
Найди периметр каждого из получившихся прямоугольников.
СРОЧНО какую часть прямоугольника составляет каждый квадрат?
СРОЧНО какую часть прямоугольника составляет каждый квадрат?
1 / 2 же, по рисунку понятно : ).
Какую часть площади прямоугольника ABCD составляет площадь закрашенного прямоугольника?
Какую часть площади прямоугольника ABCD составляет площадь закрашенного прямоугольника?
От прямоугольника отрезали квадрат со стороной 6 см?
От прямоугольника отрезали квадрат со стороной 6 см.
Найдите периметр прямоугольника, если площадь оставшейся части прямоугольника составляет 1 / 3 площади квадрата.
Два одинаковых прямоугольника составляет квадрат периметр которого 40 см Вычисли площадь каждого прямоугольника?
Два одинаковых прямоугольника составляет квадрат периметр которого 40 см Вычисли площадь каждого прямоугольника.
Какую часть один метр в кубе составляет один см в кубе?
Какую часть один метр в кубе составляет один см в кубе?
Какую часть один метр в квадрате составляет один см в квадрате?
Длина прямоугольника k метров?
Длина прямоугольника k метров.
Его ширина составляет 3 / 4 длины, а сторона квадрата составляет 4 / 3 длины прямоугольника.
Какую часть периметр прямоугольника составляет от периметра квадрата?
Квадрат разделили на равные части?
Квадрат разделили на равные части.
Какую долю целого квадрата составляет каждая из них?
От прямоугольника отрезали квадрат со стороной 6 см?
От прямоугольника отрезали квадрат со стороной 6 см.
Найдите периметр прямоугольника, если площадь оставшейся части прямоугольника составляет 1 / 3 площади квадрата.
Какую часть один метр в кубе составляет 1 сантиметр в кубе Какую часть один метр в квадрате составляет 1 сантиметр в квадрате?
Какую часть один метр в кубе составляет 1 сантиметр в кубе Какую часть один метр в квадрате составляет 1 сантиметр в квадрате.
Какие утверждения верны какие нет : все квадраты являются прямоугольниками?
Какие утверждения верны какие нет : все квадраты являются прямоугольниками?
Некоторые прямоугольники являются квадратами?
Каждый прямоугольник является четырехугольником?
Олимпиада по математике школьный этап 2021 ВОШ задания и ответы для 4-11 класса
ПОДЕЛИТЬСЯ
Задания и ответы школьного этапа 2021 олимпиады по математике для 4-11 класса всероссийской олимпиады школьников 2021-2022 учебного года, официальная дата проведения олимпиады в Омске: 06.10.2021 (6 октября 2021 года)
Задания и ответы для 4 класса: скачать
Задания и ответы для 5 класса: скачать
Задания и ответы для 6 класса: скачать
Задания и ответы для 7 класса: скачать
Задания и ответы для 8 класса: скачать
Задания и ответы для 9 класса: скачать
Задания и ответы для 10 класса: скачать
Задания и ответы для 11 класса: скачать
Интересные задания и ответы олимпиады:
1)Ваня представил число 100 в виде суммы 14 слагаемых, имеющих одинаковую сумму цифр: 100=20+20+20+20+2+2+2+2+2+2+2+2+2+2 (сумма цифр числа 20 равна 2+0=2). Вася смог представить число 100 в виде суммы 11 слагаемых, имеющих одинаковую сумму цифр. Как он это сделал? Достаточно привести один пример такого представления.
Ответ: 100=50+5+5+5+5+5+5+5+5+5+5.
2)Вера, накопив 200 рублей, хотела купить пенал, но этих денег ей не хватило. Через несколько дней пенал уценили, и он стал стоить в два раза меньше. Теперь Вера смогла его купить и даже получила сдачу 15 рублей. Сколько стоил пенал первоначально? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 370 р.
3)Фермер огородил снаружи участок земли и разделил его на квадратики со стороной 3 м. В пяти квадратиках он разместил гусятники (обозначены «Г»), а в других пяти – будки со сторожевыми собаками (обозначены «С»). Но гуси нападают на собак, а собаки могут загрызть гусей. Помогите фермеру построить по линиям сетки дополнительные заборы общей длины 30 м, чтобы защитить собак от гусей и гусей от собак.
Ответ: например, так, как на рисунке справа.
4)По кругу стоят 10 сорочат. Мама–сорока кормит их кашей: первому – 1 ложку, второму – 2 ложки, следующему – 1, потом – 2 и так далее. Всего она раздала 55 ложек каши, и на этом каша закончилась. Сколько сорочат получили ровно 4 ложки каши? Ответ нужно обосновать.
Ответ: 4 птенца
5)Никита записал два нечётных числа, а потом заменил в них разные цифры разными буквами, а одинаковые – одинаковыми. У Никиты получились два слова: УЧИТЕЛЯ и МЕЧТАТЕЛИ. Известно, что произведение цифр числа УЧИТЕЛЯ не равно нулю, а произведение цифр числа МЕЧТАТЕЛИ равно нулю. Чётной или нечётной будет сумма Я+И+МЕЧТА? Ответ нужно обосновать.
Ответ: чётная
6)В семье Веснушкиных три человека, и у каждого на лице в два раза больше веснушек, чем ему лет. Васе сейчас 11 лет. Васина мама младше Васиного папы на 3 года, и у неё на лице 66 веснушек. Сколько веснушек на лице у всех троих вместе? Ответ нужно подтвердить вычислениями и объяснениями.
Ответ: 160 веснушек.
7)Найдите какое-нибудь решение неравенства М Ответ: например, М=1, А=3, Т=2, Е=4, И=5, К=9, т.е. 1
8)Маша попросила встать 30 одноклассников по кругу и стала раздавать им шоколадные конфеты. Первому дала 1 конфету, второму – 2 конфеты, следующему – снова 1 конфету, потом – 2 конфеты и так далее. Всего она раздала 55 конфет, и на этом конфеты закончилась. Сколько Машиных одноклассников получили ровно 2 конфеты? Ответ нужно обосновать
Ответ: 16 человек
9)На рисунке слева изображена фигура на клетчатой бумаге. Сторона каждой клетки равна 1 см. Разрежьте данную фигуру по линиям сетки на фигурки, удовлетворяющие всем четырём условиям: 1) площадь каждой равна 5 см2 ; 2) периметр каждой равен 12 см; 3) все фигурки должны быть различными, т.е. не совпадать при наложении; 4) в каждой должен быть ровно один серый квадратик. Достаточно привести один вариант разрезания.
Ответ: например, как на рисунке ниже.
10)Винни-Пух, Пончик и Карлсон приняли участие в турнире обжор. По результатам трёх туров судья заполнил таблицу, где указал, сколько пирогов в каждом туре съел каждый участник. Оказалось, что все числа в таблице различны. Ночью каждый из участников увеличил только один из своих результатов в таблице на 1. Утром все увидели следующую таблицу.
Ответ: см. файл выше
11)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
12)Мальвина написала на доске выражение М+А = Т+Е = М+А+Т = И+К+А и попросила Буратино заменить все буквы цифрами так, чтобы равенства оказались верными. Причем разные буквы нужно заменять разными цифрами, а одинаковые буквы ‒ одинаковыми цифрами. Помогите Буратино справиться с задачей. Достаточно привести хотя бы один пример.
Ответ: пусть М=5, А=2, Т=0, Е=7, И=1, К=4. Тогда получим верные равенства: 5+2=0+7=5+2+0=1+4+2.
13)Семи детям раздали 55 конфет. После этого первыйсказал, что по крайней мере 1 конфета у него имеется. «А у меня ровно на две больше!» — сказал второй. «А у меня ровно на две больше, чем у тебя!» — сказал третийвторому, затем такую же фразу произнес четвертый— третьему, пятый – четвертому, шестой— пятому. А седьмой заявил: «А у меня конфет больше всех!». Сколько конфет получил седьмой ребенок? Найдите все варианты и докажите, что других нет.
Ответ: 13 или 19
14)У Алисы есть три деревянных кубика. Длина ребра меньшего кубика равна 1 дм, среднего — 2 дм, большего — 3 дм. На покраску меньшего кубика ей потребовалось на 120 г краски меньше, чем на покраску среднего кубика. Сколько граммов краски ей потребуется на покраску большего кубика?
Ответ: 360 г.
15)Чтобы насытиться, голодному кролику нужно съесть ровно три каких-нибудь различных овоща. Какое наибольшее количество голодных кроликов можно накормить досыта, если в запасах имеется 5 кукуруз, 8 огурцов, 11 морковок и 17 перцев? Ответ нужно обосновать.
Ответ: 12
16)На клетчатой бумаге нарисован прямоугольник 3х4 клетки. Разрежьте его по сторонам клеток на 3 части так, чтобы из них можно было сложить фигуру, изображенную справа.
Ответ: вариант разрезания приведен: 1-я часть с цифрами «1», 2-я часть – «2» и 3-я часть – «3». Из них легко складывается нужная фигура.
17)Замените буквы A, B, C, D, E, F, G, K цифрами от 1 до 8 без повторений так, чтобы числа 6, 11, 16, 21 в серых треугольниках являлись суммами цифр, стоящих в трёх белых треугольниках, соседствующих по сторонам с серым.
Ответ: подходящие значения букв: А=2, В=3, С=5, D=1, Е=8, F=4, G=6, К=7. Легко проверить, что условие задачи выполняется.
18)Рыбак поймал 6 кг рыбы. Часть приготовил себе, остальное отдал трём котам. Каждый кот съедает в 2 раза больше рыбы, чем рыбак за одно и то же время. Сколько килограммов рыбы было отдано котам, если есть все начали одновременно, а коты съели свою часть в 2 раза быстрее, чем рыбак?
Ответ: 4,5 кг.
19)Три одинаковых кубика приставлены друг к другу гранями с одинаковым числом очков. Найдите сумму чисел на трёх нижних гранях кубиков данной конструкции, на верхних гранях которых числа 3, 5 и 6.
Ответ: 7
20)Лиса Алиса, Буратино и Пьеро нашли 110 золотых монет. Алиса предложила разложить их на три кучки и сказала: «Пусть жребий определит, кому какая достанется!» Чтобы мальчики не расстраивались, они договорились уравнять свои кучки по меньшей, а лишнее отдать Алисе. (Например, если Буратино достанется 10 монет, Пьеро – 15, а Алисе – 85 монет, то Пьеро отдаст Алисе 5 монет, чтобы у него с Буратино стало поровну). Алисе необходимо разложить все монеты на три кучки так, чтобы в результате ей наверняка досталось не меньше 100 золотых монет. Сколько у нее есть вариантов?
Ответ: 15
21)Сколько раз в последовательности из 12 чисел: 2, _, _, _, _, _, _, _, _, _, _,1 (на первом месте стоит 2, на последнем месте 1) встретится цифра 2, если известно, что сумма любых трех чисел, идущих подряд, равна 5?
Ответ: 8 раз
22)На турнир «рыцарей и лжецов» математического кружка ребята мастерили из квадратного листа картона размером 150см×150см стену рыцарского замка. По краям и в середине было вырезано три одинаковых квадрата. Петя заметил, что при этом периметр первоначального листа увеличился на 8%. Найдите площадь получившейся «стены».
Ответ: 20772 см2
23)Петя и Вася живут в одном доме и выходят в школу одновременно. Петя сначала считает ворон и идет со скоростью 4 км/ч, но ровно на середине пути на парковке пересаживается на велосипед и едет со скоростью 12 км/ч. Вася идет в школу с постоянной скоростью и приходит в школу одновременно с Петей. Учитель Степан Иванович на середине пути обгоняет Петю на мопеде, так как его скорость в 5 раз больше скорости Васи, он приезжает в щколу на 3 минуты раньше мальчиков. Найдите расстояние от дома мальчиков до школы.
Ответ: 2км
24)По данным, изображенным на рисунке справа, найти длину катета BC прямоугольного треугольника АВС.
Ответ: 12
25)Какое наибольшее число «тетраминошек» (как на рисунке) можно разместить внутри квадрата 6×6 без наложений? Фигурки можно как угодно поворачивать и переворачивать.
Ответ: 8
26)Назовем прямоугольник «симпатичным», если его длинная сторона меньше удвоенной короткой. (В частности, квадрат является симпатичным прямоугольником). Разрежьте квадрат площади 100 на четыре симпатичных прямоугольника с площадями 10, 20, 30 и 40.
28)Винни-Пух заготовил мёд на зиму в нескольких полных горшочках по 5 литров каждый. Если бы он свои запасы мёда разлил в 4-литровые горшочки, то их потребовалось бы на четыре больше, правда, один горшочек оказался бы неполным. А если разлить весь мёд в горшочки по 7 литров, то их потребовалось бы на четыре меньше первоначального количества. Но один горшочек снова оказался бы неполным. Сколько горшочков мёда заготовил Винни-Пух?
29)Из вершин А, В и С треугольника АВС провели соответственно медиану АМ, биссектрису ВK и высоту СH. Оказалось, что середина отрезка ВK совпадает с серединой отрезка MH. Найдите углы треугольника АВС.
30)На каникулах для всех желающих провели турнир по шашкам. Каждый сыграл с каждым ровно одну партию. За победу в партии участник турнира получал 2 очка, за ничью – 1 очко, за проигрыш – 0 очков. Известно, что среди участников мальчиков было в десять раз больше, чем девочек, и они вместе набрали в 4,5 раза больше очков, чем девочки. Сколько очков набрала самая успешная девочка?
31)Девятиклассник Дима выписывает ряд последовательных трёхзначных чисел так, чтобы каждое число делилось нацело на свою последнюю цифру. Какое наибольшее количество чисел могло быть в этом ряду?
32)Имеется сталь двух сортов с содержанием никеля 55% и 12%. Сколько нужно взять металла каждого из сортов, чтобы получить 2021 т стали с содержанием 32% никеля?
33)Вася выписывает последовательность из 2021 натуральных чисел, начиная с некоторого числа, так, чтобы сумма любых трех подряд идущих чисел была равна 5. Какое наибольшее количество двоек у него может получиться?
34)На стороне ВС треугольника АВС выбрана точка F. Оказалось, что отрезок AF пересекает медиану BD в точке Е так, что АЕ = ВС. Докажите, что BF = FE.
35)Имеются две бочки с водой бесконечной вместимости и два ковшика объемами 2 и 2 2 литров. Можно ли, пользуясь этими ковшиками, перелить из одной бочки в другую ровно 1 литр?
36)От 2 кусков сплавов с разным содержанием свинца массой 6 кг и 12 кг отрезали по куску равной массы. Каждый из отрезанных кусков сплавили с остатком другого сплава, после чего процентное содержание свинца в обоих сплавах стало одинаковым. Каковы массы отрезанных кусков?
37)Художник Петров красит плоскость в два цвета произвольным образом, а геометр Васильев утверждает, что сможет построить треугольник с вершинами одного цвета, величины углов которого относятся как 4:2:1. Прав ли он?
Разрезание прямоугольника
Задача
Прямоугольник разрезан на 9 квадратов, как показано на рисунке. Сторона маленького белого квадрата равна 1.
Найдите стороны прямоугольника.
Подсказка
Можно, конечно, просто взять линейку и измерить длины отрезков на рисунке, но этот способ не очень хороший по двум причинам. Во-первых, точность таких измерений не слишком высока и ответ получится лишь приближенный. Во-вторых, если бы в нашем распоряжении оказалась картинка «под углом», то истинные длины сторон на ней были бы искажены, и тогда пришлось бы еще думать, что делать с измерениями. Но можно найти стороны прямоугольника абсолютно точно, и знать для этого необходимо только схему разрезания. Для этого нужно составить систему уравнений, приняв за неизвестные длины сторон квадратов и прямоугольника.
Решение
Как уже было отмечено в подсказке, эта задача вовсе не по геометрии (как могло бы показаться), а по линейной алгебре. Причем, решается она довольно просто. Нужно лишь не побояться сначала ввести много обозначений.
Рис. 1. Пронумеруем квадраты
Итак, пусть x и y — ширина и высота большого прямоугольника, которые мы ищем. Пронумеруем квадраты, как показано на рисунке 1, и обозначим сторону квадрата с номером i через zi. Переменные уже есть. А откуда взять уравнения? Посмотрим внимательно на рисунок 1: видно, что некоторые стороны квадратов «хорошо» примыкают друг к другу. Например, белый квадратик дополняет сторону красного квадрата до стороны оранжевого. Еще пример: белый вместе с желтым по высоте занимают столько же, сколько голубой с пурпурным. Эти условия стыковки и позволяют написать уравнения. Получится система линейных уравнений, которую запишем в два приема. Сначала выпишем уравнения, которые отвечают вертикальным стыкам:
Последнее уравнение описывает примыкание третьего и восьмого квадратов к правой стороне прямоугольника. Но оно следует из предыдущих уравнений (проверьте это), поэтому далее его не учитываем. Теперь выпишем уравнения на горизонтальные стыки (условие для нижней стороны пропускаем по той же причине):
Объединим всё в одну систему, из которой нам и нужно найти x и y:
Для решения систем линейных уравнений давно придумано множество методов. Но в нашем случае можно обойтись и без привлечения мощных теорий, а просто последовательно выражать одни переменные через другие и делать соответствующие подстановки, постепенно упрощая систему. Удобно выражать переменные через z5: z2 = 1 + z5, значит z1 = 2 + z5, значит z4 = 3 + z5. Уже можно явно вычислить сторону голубого квадрата: z6 = 1 + z4 – z5 = 4. Продолжая в том же духе, несложно найти стороны остальных квадратов, а вместе с ними и стороны прямоугольника: x = 32, а y = 33.
Послесловие
Возможно, решение этой задачи поможет вам сделать что-нибудь вроде такого шкафа:
Или еще что-нибудь не менее прекрасное.
Вообще, вопросы о разрезаниях разных фигур на специфические части обычно бывают интересными и красивыми. Причем рассчитаны они могут быть на самую разную аудиторию: задачки такого рода часто дают на математических кружках, но, как мы только что убедились, бывают и не очень «кружковские» задачи.
Про разрезания именно прямоугольников известно многое. Вполне очевидно, что если отношение сторон прямоугольника рационально, то его можно разрезать на одинаковые квадраты. А если можно резать на необязательно одинаковые квадраты, то что тогда? В 1903 году Макс Ден (Max Dehn) доказал, что и в этом случае отношение сторон прямоугольника должно быть рационально (кстати, имя этого немецкого математика уже встречалось ранее в одной из задач на «Элементах»). Его доказательство было сложным, но позднее был придуман более простой способ. Вкратце его суть такова. Оказывается, по любому разрезанию прямоугольника можно построить специальную электрическую цепь, и это сопоставление настолько удачно, что условия состыкования сторон квадратов идентичны правилам Кирхгофа для этой цепи. Поскольку эти правила позволяют полностью рассчитать электрическую цепь, то это позволяет найти и размеры квадратов. Подробнее об этом можно прочитать в статье М. Скопенкова, М. Прасолова и С. Дориченко «Разрезания металлического прямоугольника» («Квант» №3, 2011), на основе которой был подготовлен этот материал.
Есть еще одна похожая по формулировке задача про разрезание прямоугольников: прямоугольник как-то разрезан на прямоугольники, причем известно, что хотя бы одна из сторон каждого из них имеет целую длину; требуется доказать, что тогда и у большого прямоугольника будет целая сторона. А вот решение у нее довольно далекое от рассмотренных выше идей. Если у вас не получится решить эту задачу, то прочитать ее решение можно, например, здесь.