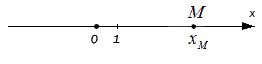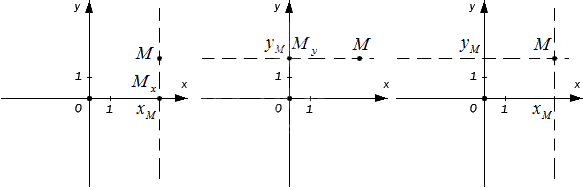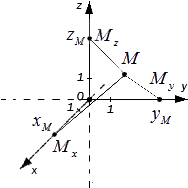Как называются координаты точки в пространстве

Прямоугольная система координат. Ось абсцисс и ординат

Прямоугольная декартова система координат

Французский математик Рене Декарт предложил вместо геометрических построений использовать математические расчеты. Так появился метод координат, о котором мы сейчас расскажем.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты школы тоже можно записать числами — они помогут понять, где именно находится наша школа. С точками на плоскости та же история.

Координатой можно назвать номер столика в кафе, широту и долготу на географической карте, положение точки на числовой оси и даже номер телефона друга. Проще говоря, когда мы обозначаем какой-то объект набором букв, чисел или других символов, тем самым мы задаем его координаты.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Единичные отрезки располагаются справа и слева от оси Oy, вверх и вниз от оси Oy. Числовые значения на оси Oy располагаются слева или справа, на оси Ox — внизу под ней. Чаще всего единичные отрезки двух осей соответствуют друг другу, но бывают задачи, где они не равны.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Чтобы узнать координаты точки в прямоугольной системе координат, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра. Координаты записывают в скобках, первая по оси Ох, вторая по оси Оу.

Курсы подготовки к ОГЭ по математике от Skysmart придадут уверенности в себе и помогут освежить знания перед экзаменом.

Координаты точки в декартовой системе координат

Для начала отложим точку М на координатной оси Ох. Любое действительное число x_M равно единственной точке М, которая располагается на данной прямой. При этом начало отсчета координатных прямых всегда ноль.

Каждая точка М, которая расположена на Ох, равна действительному числу x_M. Этим действительным числом и является ноль, если точка М расположена в начале координат, то есть на пересечении Оx и Оу. Если точка удалена в положительном направлении, то число длины отрезка положительно и наоборот.

Число x_M — это координата точки М на заданной координатной прямой.

Пусть точка будет проекцией точки M_x на Ох, а M_y на Оу. Значит, через точку М можно провести перпендикулярные осям Оx и Оу прямые, после чего получим соответственные точки пересечения M_x и M_y.Тогда у точки M_x на оси Оx есть соответствующее число x_M, а M_y на Оу — y_M. Как это выглядит на координатных осях:

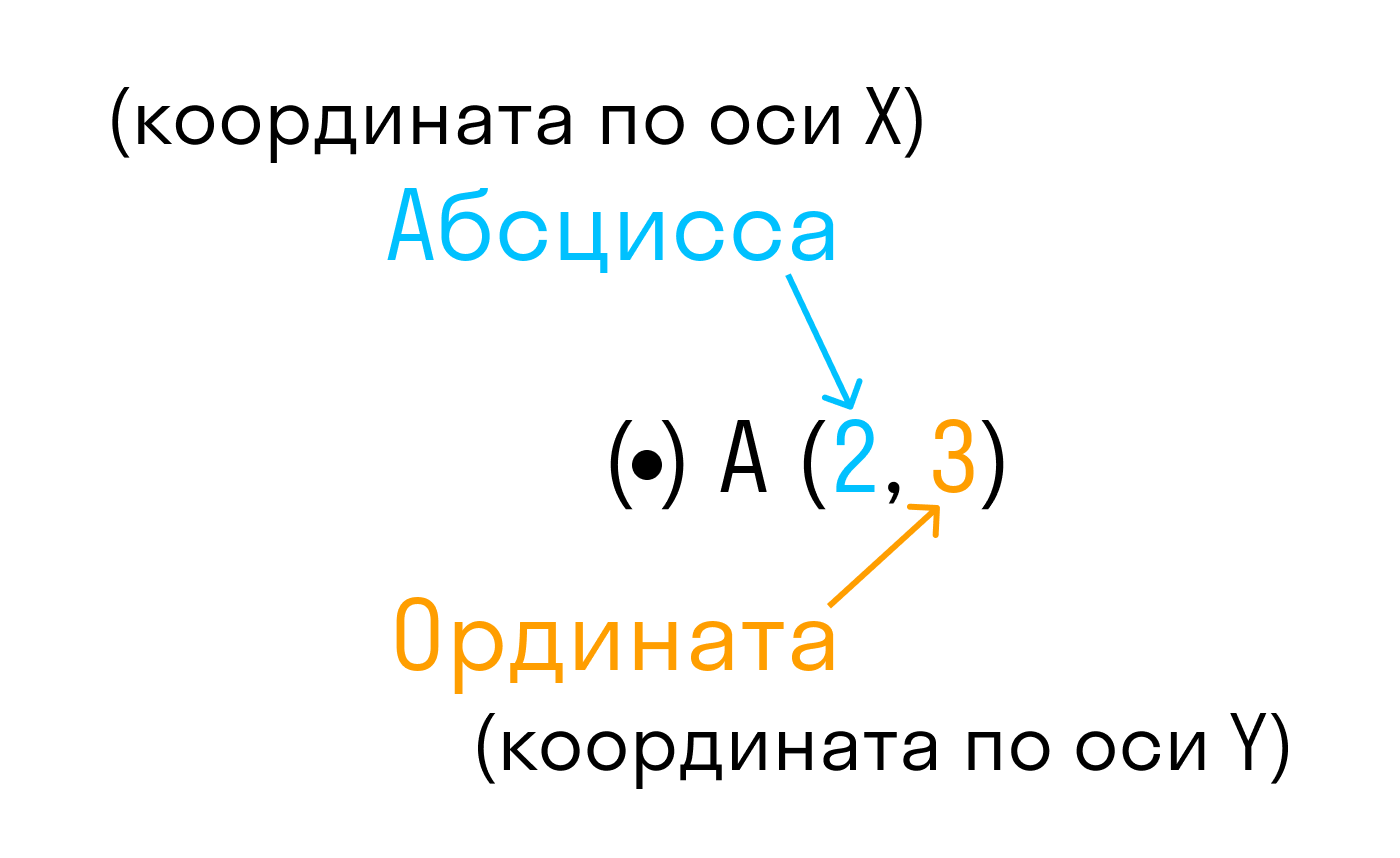
Каждой точке М на заданной плоскости в прямоугольной декартовой системе координат соответствует пара чисел (x_M, y_M), которые называются ее координатами. Абсцисса М — это x_M, ордината М — это y_M.

Обратное утверждение тоже верно: каждая пара (x_M, y_M) имеет соответствующую точку на плоскости.

Источник

Прямоугольная система координат на плоскости и в пространстве

При введении системы координат на плоскости или в трехмерном пространстве появляется уникальная возможность описания геометрических фигур и их свойств при помощи уравнений и неравенств. Это имеет иное название – методы алгебры.

Данная статья поможет разобраться с заданием прямоугольной декартовой системой координат и с определением координат точек. Более наглядное и подробное изображение имеется на графических иллюстрациях.

Прямоугольная декартова система координат на плоскости

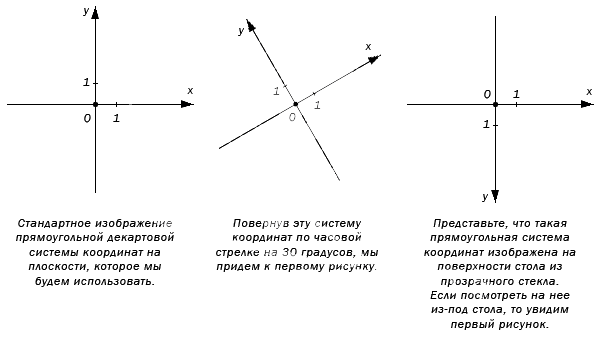
Изображение прямоугольной системы координат на плоскости.

Оси абсцисс и ординат имеют одинаковую единицу изменения и масштаб, что показано в виде штрихе в начале координатных осей. Стандартное направление О х слева направо, а O y – снизу вверх. Иногда используется альтернативный поворот под необходимым углом.

Прямоугольная система координат получила название декартовой в честь ее первооткрывателя Рене Декарта. Часто можно встретить название как прямоугольная декартовая система координат.

Прямоугольная система координат в трехмерном пространстве

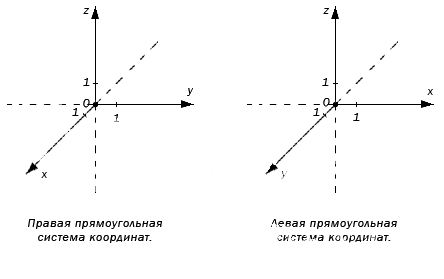
По направлению координатных осей делят на правую и левую прямоугольные системы координат трехмерного пространства.

Аналогично образуется левая система координат. Обе системы совместить невозможно, так как соответствующие оси не совпадут.

Координаты точки в декартовой системе координат на плоскости

Имеющееся число x M называют координатой точки М на заданной координатной прямой.

Координаты точки в прямоугольной системе координат в трехмерном пространстве

Источник

Как найти координаты точки?

3 класс, 4 класс, 9 класс, 11 класс, ЕГЭ/ОГЭ

Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат (в правом нижнем углу экрана).

Понятие системы координат

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве. Например, координаты вашей квартиры тоже можно записать числами — они помогут понять, где именно находится тот дом, где вы живете. С точками на плоскости та же история.

Прямоугольная система координат — это система координат, которую изобрел математик Рене Декарт, ее еще называют «декартова система координат». Она представляет собой два взаимно перпендикулярных луча с началом отсчета в точке их пересечения.

Чтобы найти координаты, нужны ориентиры, от которых будет идти отсчет. На плоскости в этой роли выступят две числовые оси.

Для тех, кто хочет связать свою жизнь с точными науками, Skysmart предлагает курсы по профильной математике.

Чертеж начинается с горизонтальной оси, которая называется осью абсцисс и обозначается латинской буквой x (икс). Записывают ось так: Ox. Положительное направление оси абсцисс обозначается стрелкой слева направо.

Затем проводят вертикальную ось, которая называется осью ординат и обозначается y (игрек). Записывают ось Oy. Положительное направление оси ординат показываем стрелкой снизу вверх.

Оси взаимно перпендикулярны, а значит угол между ними равен 90°. Точка пересечения является началом отсчета для каждой из осей и обозначается так: O. Начало координат делит оси на две части: положительную и отрицательную.

Оси координат делят плоскость на четыре угла — четыре координатные четверти.

У каждой из координатных четвертей есть свой номер и обозначение в виде римской цифры. Отсчет идет против часовой стрелки:

Определение координат точки

Каждой точке координатной плоскости соответствуют две координаты.

Точка пересечения с осью Ох называется абсциссой точки А, а с осью Оу называется ординатой точки А.

Чтобы узнать координаты точки на плоскости, нужно опустить от точки перпендикуляр на каждую ось и посчитать количество единичных отрезков от нулевой отметки до опущенного перпендикуляра.

Координаты точки на плоскости записывают в скобках, первая по оси Ох, вторая по оси Оу.

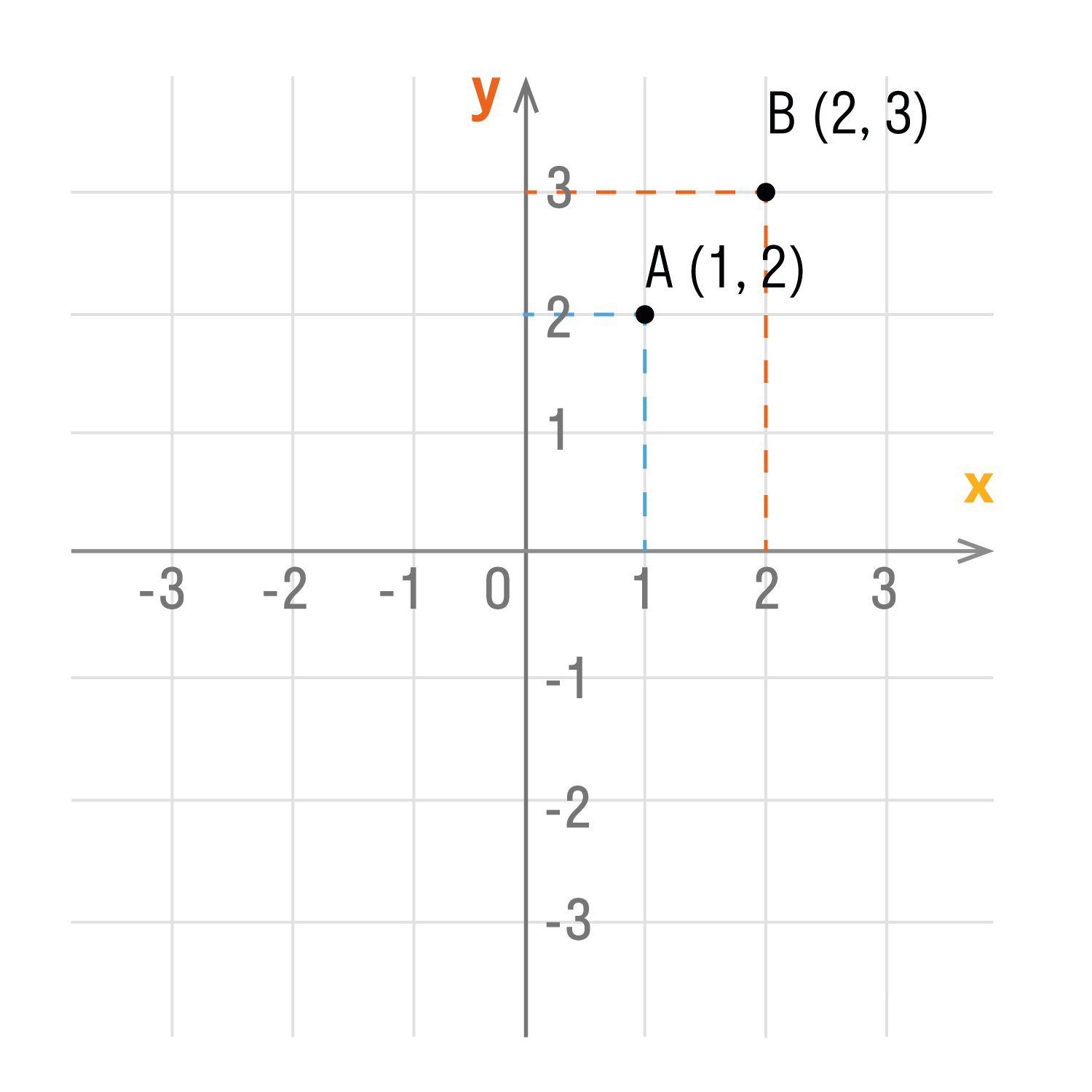
Смотрим на график и фиксируем: A (1; 2) и B (2; 3).

Особые случаи расположения точек

В геометрии есть несколько особых случаев расположения точек. Лучше их запомнить, чтобы без запинки решать задачки. Вот они:

Способы нахождения точки по её координатам

Чтобы узнать, как найти точку в системе координат, можно использовать один из двух способов.

Способ первый. Как определить положение точки D по её координатам (-4, 2):

Способ второй. Как определить положение точки D (-4, 2):

Чтобы легко и быстро находить координаты точек или строить точки по координатам, скачайте готовую систему координат и храните ее в учебнике:

Источник

Геометрия. 11 класс

Конспект урока

Геометрия, 11 класс

Урок № 1. Координаты в пространстве. Система координат

Перечень вопросов, рассматриваемых в теме:

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/

Теоретический материал для самостоятельного изучения

Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью. Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.

Прямоугольная система координат в пространстве задана, если выбрана точка – начало координат, через эту точку проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и задана единица измерения отрезков (рис. 121). Прямые с выбранными на них направлениями называются осями координат, а их общая точка – началом координат.

причем коэффициенты разложения х, у, z определяются единственным образом.

Коэффициенты х, у и z в разложении вектора по координатным векторам называются координатами вектора в данной системе координат. Координаты вектора будем записывать в фигурных скобках после обозначения вектора: <х; у; z>.

Нулевой вектор можно представить в виде так как все координаты нулевого вектора равны нулю.

Так как нулевой вектор можно представить в виде то все координаты нулевого вектора равны нулю. Далее, координаты равных векторов соответственно равны, т. е. если векторы <х₁, y₁, z₁> и <х_2, y₂, z₂) равны, то х₁ = x₂, y₁ = y₂ и z₁ = z₂

Рассмотрим правила, которые позволяют по координатам данных векторов найти координаты их суммы и разности, а также координаты произведения данного вектора на данное число.

1)Каждая координата суммы двух или более векторов равна сумме соответствующих координат этих векторов. Другими словами, если <х₁, у₁, z₁> и <х₂, у₂, z₂> — – данные векторы, то вектор + имеет координаты <х₁+х₂, у₁ + у₂, z₁ + z₂>.

2)Каждая координата разности двух векторов равна разности соответствующих координат этих векторов. Другими словами, если <х₁, y₁, z_1> и b<х₂ у₂; z₂> – данные векторы, то вектор – имеет координаты <х₁ – х₂, y₁ – y₂, z₁ – z₂>.

3)Каждая координата произведения вектора на число равна произведению соответствующей координаты вектора на это число. Другими словами, если <х; у; х>– данный вектор, α – данное число, то вектор α имеет координаты <αх; αу; αz).

1)Признак коллинеарности векторов: Для того, чтобы два вектора были коллинеарны, необходимо и достаточно, чтобы один из них был произведением другого на некоторое число.

Определение: Векторы называются компланарными, если при откладывании их от одной и той же точки они будут лежать в одной плоскости.

Каждая координата вектора равна разности соответствующих координат его конца и начала.

Каждая координата середины отрезка равна полусумме соответствующих координат его концов.

Длина вектора вычисляется по формуле:

Примеры и разбор решения заданий тренировочного модуля

Выделите цветом верный ответ:

Найти: координаты точки D.

поэтому 18

Дано: координаты точек: А (3; –1; 2), В (x; ); координаты вектора

Решаем уравнения и получаем: х=8; у= ; z=3, z=-1

Источник

Как называются координаты точки в пространстве

Если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление (оно обозначается стрелкой) и выбрана единица измерения отрезков, то говорят, что задана прямоугольная система координат в пространстве.
Прямые с выбранными на них направлениями называются осями координат, а их общая точка — началом координат. Она обозначается обычно буквой О.
Оси координат обозначаются так: Ох, Оу, Оz — и имеют названия: ось абсцисс, ось ординат, ось аппликат. Вся система координат обозначается Охуz.
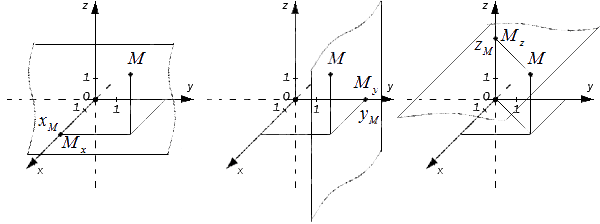
Плоскости, проходящие соответственно через оси координат Ох и Оу, Оу и Оz, Оz и Ох, называются координатными плоскостями и обозначаются Оху, Оуz, Оzх.
Точка О разделяет каждую из осей координат на два луча. Луч, направление которого совпадает с направлением оси, называется положительной полуосью, а другой луч отрицательной полуосью.

Если точка А (х; у; z) лежит на координатной плоскости или на оси координат, то некоторые ее координаты равны нулю.

Источник