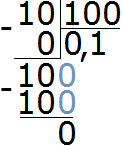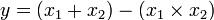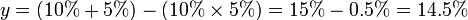Как называют проценты с процентов
Проценты
Процент это один из интересных и часто применяемых на практике инструментов. Проценты частично или полностью применяются в любой науке, на любой работе и даже в повседневном общении. Человек, хорошо разбирающийся в процентах, создаёт впечатление умного и образованного. В данном уроке мы узнаем, что такое процент и какие действия можно с ним выполнять.
Что такое процент?
В повседневной жизни дроби встречаются наиболее часто. Они даже получили свои названия: половина, треть и четверть соответственно.
Но есть ещё одна дробь, которая тоже встречается часто. Это дробь (одна сотая). Данная дробь получила название процент.
Дробь означает, что нечто разделено на сто частей и от этих ста частей взята одна часть. Значит процентом является одна сотая часть.
Процентом является одна сотая часть
Например, 
от одного метра составляет 1 см. Один метр разделили на сто частей, и взяли одну часть (вспоминаем, что 1 метр это 100 см). А одна часть из этих ста частей составляет 1 см. Значит один процент от одного метра составляет 1 см.
от одного метра уже составляет 2 сантиметра. В этот раз один метр разделили на сто частей и взяли оттуда не одну, а две части. А две части из ста составляют два сантиметра. Значит два процента от одного метра составляет 2 сантиметра.
Еще пример, от одного рубля составляет одну копейку. Рубль разделили на сто частей, и взяли оттуда одну часть. А одна часть из этих ста частей составляет одну копейку. Значит один процент от одного рубля составляет одну копейку.
Проценты встречались настолько часто, что люди заменили дробь на специальный значок, который выглядит следующим образом:
Эта запись читается как «один процент». Она заменяет собой дробь . Также она заменяет собой десятичную дробь 0,01 потому что если перевести обычную дробь в десятичную дробь, то мы получим 0,01. Стало быть между этими тремя выражениями можно поставить знак равенства:
1% = = 0,01
Как найти процент?
Принцип нахождения процента такой же, как и обычное нахождение дроби от числа. Чтобы найти процент от чего-либо, нужно это чего-либо разделить на 100 частей и полученное число умножить на нужный процент.
Например, найти 2% от 10 см.
А как решать подобные задания мы уже знаем. Это обычное нахождение дроби от числа. Чтобы найти дробь от числа, нужно это число разделить на знаменатель дроби, и полученный результат умножить на числитель дроби.
Итак, делим число 10 на знаменатель дроби
Получили 0,1. Теперь 0,1 умножаем на числитель дроби
Получили ответ 0,2. Значит 2% от 10 см составляет 0,2 см. А если перевести 0,2 сантиметра в миллиметры, то получим 2 миллиметра:
Значит 2% от 10 см составляют 2 мм.
Пример 2. Найти 50% от 300 рублей.
Чтобы найти 50% от 300 рублей, нужно эти 300 рублей разделить на 100, и полученный результат умножить на 50.
Итак, делим 300 рублей на 100
Теперь полученный результат умножаем на 50
Значит 50% от 300 рублей составляет 150 рублей.
Если на первых порах сложно привыкнуть к записи со значком %, можно заменять эту запись на обычную дробную запись.
В принципе, ничего сложного здесь нет. Если возникают сложности, советуем остановиться и заново изучить дроби и как их можно применять.
Пример 3. Швейная фабрика выпустила 1200 костюмов. Из них 32% составляют костюмы нового фасона. Сколько костюмов нового фасона выпустила фабрика?
Здесь нужно найти 32% от 1200. Найденное число будет ответом к задаче. Воспользуемся правилом нахождения процента. Разделим 1200 на 100 и полученный результат умножим на искомый процент, т.е. на 32
Ответ: 384 костюмов нового фасона выпустила фабрика.
Второй способ нахождения процента
Второй способ нахождения процента намного проще и удобнее. Он заключается в том, что число от которого ищется процент сразу умножит на нужный процент, выраженный в виде десятичной дроби.
Например, решим предыдущую задачу этим способом. Найти 50% от 300 рублей.
Запись 50% заменяет собой запись 
, а если перевести эти в десятичную дробь, то мы получим 0,5
Теперь для нахождения 50% от 300, достаточно будет умножить число 300 на десятичную дробь 0,5
Кстати, по этому же принципу работает механизм нахождения процента на калькуляторах. Чтобы найти процент с помощью калькулятора, нужно ввести в калькулятор число от которого ищется процент, затем нажать клавишу умножения и ввести искомый процент. Затем нажать клавишу процента %
Нахождения числа по его проценту
Зная процент от числа, можно узнать всё число. Например, предприятие выплатило нам 60000 рублей за работу, и это составляет 2% от общей прибыли, полученной предприятием. Зная свою долю, и сколько процентов она составляет, мы можем узнать общую прибыль.
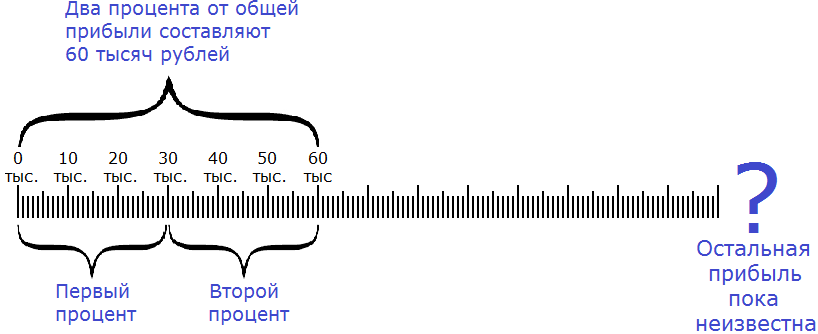
Сначала нужно узнать сколько рублей составляет один процент. Как это сделать? Попробуйте догадаться внимательно изучив следующий рисунок:
Если два процента от общей прибыли составляют 60 тысяч рублей, то нетрудно догадаться, что один процент составляет 30 тысяч рублей. А чтобы получить эти 30 тысяч рублей, нужно 60 тысяч разделить на 2
Мы нашли один процент от общей прибыли, т.е. . Если одна часть это 30 тысяч, то для определения ста частей, нужно 30 тысяч умножить на 100
30 000 × 100 = 3 000 000
Мы нашли общую прибыль. Она составляет три миллиона.
Попробуем сформировать правило нахождения числа по его проценту.
Чтобы найти число по его проценту, нужно известное число разделить на данный процент, и полученный результат умножить на 100.
Пример 2. Число 35 это 7% от какого-то неизвестного числа. Найти это неизвестное число.
Читаем первую часть правила:
Чтобы найти число по его проценту, нужно известное число разделить на данный процент
У нас известное число это 35, а данный процент это 7. Разделим 35 на 7
Читаем вторую часть правила:
и полученный результат умножить на 100
У нас полученный результат это число 5. Умножим 5 на 100
500 это неизвестное число, которое требовалось найти. Можно сделать проверку. Для этого находим 7% от 500. Если мы всё сделали правильно, то должны получить 35
Получили 35. Значит задача была решена правильно.
Принцип нахождения числа по его проценту такой же, как и обычное нахождение целого числа по его дроби. Если проценты на первых порах смущают и сбивают с толку, то запись с процентом можно заменять на дробную запись.
Например, предыдущая задача может быть изложена так: число 35 это 
от какого-то неизвестного числа. Найти это неизвестное число. Как решать такие задачи мы уже знаем. Это нахождение числа по дроби. Для нахождения числа по дроби, мы это число делим на числитель дроби и полученный результат умножаем на знаменатель дроби. В нашем примере число 35 нужно разделить на 7 и полученный результат умножить на 100
В будущем мы будем решать задачи на проценты, часть из которых будут сложными. Чтобы на первых порах не усложнять обучение, достаточно уметь находить процент от числа, и число по проценту.
Проценты.
Проценты мы видим достаточно часто в повседневной жизни. Возьмем плитку шоколада, пачку мороженого на которых написано «56 % какао», «пломбир 100 % ». А что такое процент?
Процентом называется одна сотая часть. Кратко записывают 1 %. Знак % заменяет слово «процент».
Какое бы число или величину мы не взяли, его сотая часть — это один процент данного числа или величины. Например, для числа 400 (0,01 числа 400) — это число 4, поэтому 4 — это 1 % числа 400; 1 гривны (0,01 гривны) — это 1 копейка, поэтому 1 копейка — это 1 % гривны.
Пазл содержит 500 элементов. Сколько элементов приходится на 1 его процент? Пусть 500 элементов пазла — это 100 %. Тогда на 1 % приходится в 100 раз меньше его элементов. Отсюда 500 : 100 = 5 (эл.). Итак, 1 % — это 5 элементов пазла.
Марине надо пришить тесьму, 3 см которой составляет 1 % от её длины. Марина пришила 50 % тесьмы, Сколько сантиметров тесьмы она пришила? Поскольку 50 % больше 1 % в 50 раз, то Марина пришила тесьмы в 50 раз больше, чем 3 см. Отсюда 3•50 = 150 (см). Итак, Марина пришила 150 см тесьмы.
Груши сладких сортов содержат 15 % сахара. Сколько сахара содержится в 3 кг груш?
Составим краткую запись данных задачи.
1. Сколько килограммов соответствует 1 %?
2. Сколько килограммов приходится на 15 %?
И так, в 3 кг груш содержится 0,45 кг сахара.
Чтобы найти процент от числа, нужно данное число разделить на 100 и результат умножить на количество процентов.
В украинском веночке Марины 20 % всех лент голубые. Сколько всего лент в веночке, если голубых — 5?
Составим краткую запись данных задачи.
Голубые ленты: 5 — 20%
Итак, в веночке Марины 25 лент.
Чтобы найти число по его проценту, нужно данное число разделить на количество процентов и результат умножить на 100.
Достаточно часто необходимо найти процентное выражение одного числа от другого.
Завод произвел за 2014 год 40000 деталей, а в следующем году – только 36000 штук. Сколько процентов это составило по отношению к выпуску предыдущего года?
Составим краткую запись:
Итак, в 2015 выпуск составил 90 % от 2014 года
Правило нахождения процентного выражения числа от другого.
Чтобы найти процентное выражение числа от другого, нужно данное число разделить на первое и результат умножить на 100.
Процентное отношение двух чисел — это их отношение, выраженное в процентах. Процентное отношение показывает, сколько процентов одно число составляет от другого.
Процент
Понятие % (доли) чего-либо
История возникновения процентов, расчёт процента, правила набора, разговорное употребление, задачи на проценты
Содержание
Содержание
История возникновения процентов
Использование процентов в повседневной жизни
Типы задач на проценты
Проценты в программировании
процент — это одна сотая доля. Обозначается знаком «%». Используется для обозначения доли чего-либо по отношению к целому. Например, 17 % от 500 кг означает 17 частей по 5 кг каждая, то есть 85 кг. Это математическое понятие часто встречаются в повседневной жизни. Этимология термина имеет латинские корни. Слово «процент» происходит от латинского слова pro centum, что буквально переводится «за сотню», или «со ста».
Как экономическое понятие в значении «прибыль»,»выгода«, «преимущество» слово стало использоваться во второй половине 19 века.
В современной финансовой лексике процент определяется как плата за использование заемных средств, как цена рентных доходов. Когда финансисты говорят о проценте, то они имеют в виду доходность к погашению, то есть такую ставку в коэффициенте дисконтирования которая выравнивает дисконтированную (приведенную) цену будущих результатов инвестиции с ее настоящей ценой.
Понятие процента
В тексте знак процента используется только при числах в цифровой форме, от которых при наборе отделяется неразрывным пробелом (доход 67 %), кроме случаев, когда знак процента используется для сокращённой записи сложных слов, образованных при помощи числительного и прилагательного «процентный»
процент по-китайски обозначается разными словами в зависимости от того используется ли он в математическом или в экономическом смысле.В чистом виде «процент» это 百分比 (байфэньби), что дословно переводится как «отношение к ста частям». Так, например 10% будут звучать как «десять сотых». То есть, в китайском проценте обязательно есть упоминание о «ста» и нет никаких посторонних заимствованных или древних слов, а только чистая математика.
Процентное выражение в Китае часто используется в выражениях типа «за минувший год страна стала вырабатывать на 9% больше электричества». Причем, может использоваться как знак процента «%», так и дословное написание выражения «девять сотых».
Правило написания числа и знака процента раздельно введено в действие в 1982 году нормативным документом ГОСТ 8.417—81 (впоследствии заменённым на ГОСТ 8.417—2002); ранее нормой было не отделять знак процента пробелом от предшествующей цифры.
В настоящее время правило отбивки знака процента не является общепризнанным. До сих пор многие российские издательства не следуют рекомендациям ГОСТ 8.417—2002 и по-прежнему придерживаются традиционных правил набора, то есть при наборе знак процента от предшествующего числа не отделяется.
Иногда бывает удобным сравнивать две величины не по разности их значений, а в процентах. Например, цену двух товаров сравнивать не в рублях, а оценивать, насколько цена одного продукта больше или меньше цены другого в процентах. Если сравнение по разности вполне однозначно, то есть всегда можно найти, насколько одна величина больше или меньше другой, то для сравнения в процентах нужно указывать, относительно какой величины вычисляется процент. Такое указание, впрочем, необязательно в том случае, когда говорят, что одна величина больше другой на число процентов, превышающее 100. В этом случае остается только одна возможность вычисления процента, а именно деление разности меньшее из двух чисел с последующим умножением результата на 100.
Проценты в экономике
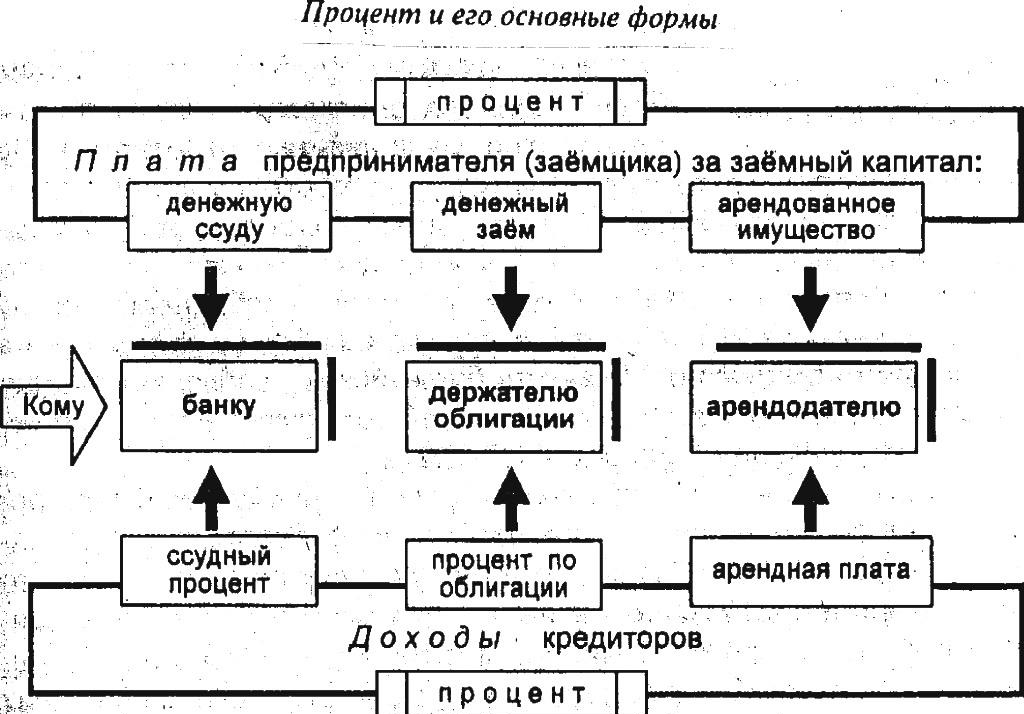
процент является частью прибыли, которую кредитор выплачивает заемщику за взятый в ссуду денежный капитал, и определяется как «иррациональная форма цены» ссудного капитала. Источником процента выступает прибавочная стоимость, создаваемая в процессе производительного использования ссудного капитала. Разделение прибыли, получаемой при использовании ссудного капитала, на процент, присваиваемый ссудным капиталом, и собственно прибыль — предпринимательский доход, получаемый кредитором, происходит под влиянием спроса и предложения на рынке ссудных капиталов. Таким образом, процент выражает отношения между заемщиком и кредитором и выступает в форме определенной процентной ставки.
В отличие от займа ссудный процент предполагает не возвратное, а безвозвратное распределение стоимости произведенного товара, причем не всей стоимости, а лишь стоимости прибавочного товара в его превращенной форме — прибыли. Процент является прямым вычетом из прибыли, остающейся в распоряжении заемщика. Величина процента зависит от уровня ставки процента и суммы ссуды, полученного кредитором.
Формирование ссудной политики коммерческого банка должно основываться на учете следующих важнейших факторов’:
— степень рискованности и прибыльность различных видов займов;
— общее состояние экономики государства;
— влияние на экономику денежно-кредитной и финансовой политики;
— способности и опыт банковского персонала;
— потребности в займах района (региона), обслуживаемого банком.
Данные факторы оказывают, бесспорно, влияние на проводимую банком ссудную процентную политику.
Современное государство с рыночной экономикой, контролируя движение ссудного процента, может влиять практически на все параметры общественного производства. В частности, поднимая ставку ссудного процента, государство через ЦБ может способствовать денежным накоплениям, снижению цен и стабилизации заработной платы, повышению эффективности производства и росту курса национальной валюты, снижению конкурентоспособности своих товаров, удорожанию экспортирования и удешевлению импорта товаров, увеличению импорта капитала и сдерживанию его экспортирования и т. д.
Повышение уровня процентных ставок по депозитам (вкладам) имеет не только экономическое значение, но и социальное. В условиях инфляции трудно обеспечить защиту интересов вкладчиков, а следовательно, они не заинтересованы в помещении средств на длительное хранение. Поэтому депозитная процентная политика банков должна увязываться с комплексным обслуживанием клиента.
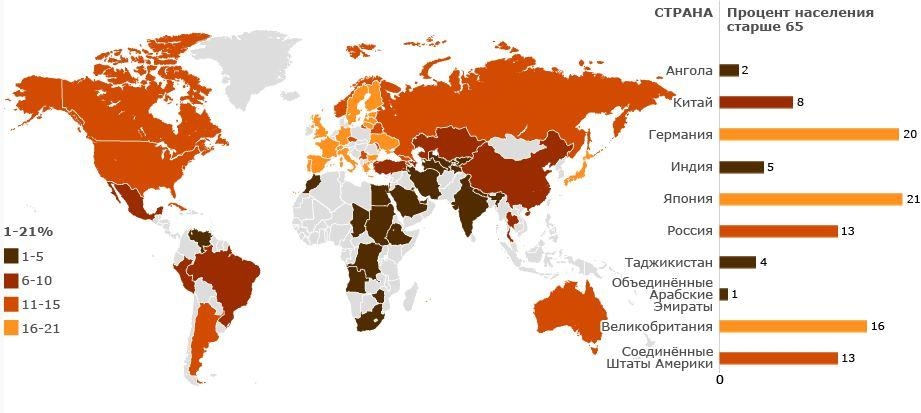
Процентные ставки по депозитам в некоторых странах зависят от суммы вкладов: с их возрастанием увеличивается доход по вкладу. В целях стимулирования сбережений, особенно на продолжительный срок, кредитные учреждения зарубежных стран платят вкладчикам достаточно высокие проценты (с учетом низкой инфляции), в частности, в США — от 5,7 до 9,8%, в Британии — от 3,0 до 11,2%, в ФРГ — от 2,5 до 5,2%, во Франции — от 4,5 до 7,5%, в Италии — от 5,0 до 12,3%.
Методы начисления процентов
В банковской практике существуют различные методы и способы начисления процентов.
Применяются простые и сложные проценты.
Простые проценты – это метод начисления, при котором сумма процентов определяется в течение всего периода, исходя из первоначальной величины долга, независимо от количества периодов начисления и их длительности.
Простой процент – это когда процент по вкладу начисляется в конце срока. Например, открыт вклад на год, с выплатой процентов в конце срока вклада.
Формула, по которой производится расчет простых процентов:
Формула сложных процентов выглядит так:
процентная ставка определяется в соответствии с конкретными условиями использования ссудного капитала и является объектом денежного и кредитного регулирования со стороны центробанка. При этом величина процентных ставок способствует либо притоку денежного капитала на внутренний рынок с денежных рынков других стран, либо его оттоку.
Коммерческие банки устанавливают ставки процентов, ориентируясь на учетные ставки, принятые в Центральных банках своих стран. При этом крупные банки определяют минимальные или лучшие ставки по ссудам, предоставляемым первоклассным заемщикам.
Важное значение в структуре процентных ставок имеют проценты по вкладам банковских клиентов. Проценты, выплачиваемые банками их клиентам, всегда существенно ниже процентов по займам (за счет этой разницы формируется один из главных источников банковской прибыли — процентная маржа)
Процентная маржа — разница между процентным выгодой и затратой коммерческого банка, процентами полученными и уплаченными. Процентная маржа (основной источник прибыли банка) должна покрывать налоги, убытки от спекулятивных операций и бремя (превышение беспроцентного дохода над беспроцентным издержкой), а также банковские риски. Ее размер можег характеризоваться абсолютной величиной и рядом финансовых коэффициентов.
Абсолютная величина маржи рассчитывается как разница между общей величиной процентного дохода и затраты банка, а также между процентным наживой по отдельным видам активных операций и процентным затратой, связанным с ресурсами, которые использованы для этих операций.
Современные подходы к формированию процентной ставки основываются фактически на четырех классических теориях процента, сформулированных К. Векселем, И. Фишером, Дж.М. Кейнсом, Д. Хиксом.
Процентная политика находит свое выражение в регулировании уровня и динамики процентных ставок. При открытой экономике уровень и динамика процентных ставок отражают степень деловой активности в стране, темпы инфляции, напряженность кредитного рынка и воздействие внешних факторов.
Процентная политика является одним из важнейших и в то же время достаточно сложных инструментов регулирования банковской деятельности. При этом основные принципы построения шкалы процентных ставок должны исходить из:
— состояния спроса и предложения на кредитные ресурсы;
— темпов инфляции и т. д.
История возникновения процентов
Процент имеет многовековую историю.
Идея выражения частей целого постоянно в одних и тех же долях, вызванная практическими соображениями, родилась еще в древности у вавилонян, которые пользовались шестидесятеричными дробями. Уже в клинописных таблицах вавилонян содержатся задачи на расчет процентов. До нас дошли составленные вавилонянами таблицы процентов, которые позволяли быстро определить сумму процентных денег. Были известны проценты и в Индии. Индийские математики вычисляли проценты, применив так называемое тройное правило, т. е. пользуясь пропорцией. Они умели производить и более сложные вычисления с применением процентов. Денежные расчеты с процентами были особенно распространены в Древнем Риме. Римляне называли процентами деньги, которые платил должник заимодавцу за каждую сотню. Даже римский cенат США вынужден был установить максимально допустимый процент, взимаемый с должника, так как некоторые заимодавцы усердствовали в получении процентных денег. От римлян проценты перешли к другим народам.
В средние века в Европе в связи с широким развитием торговли особо много внимания обращали на умение вычислять проценты. В то время приходилось рассчитывать не только проценты, но и проценты с процентов, т. е. сложные проценты, как называют их в наше время. Отдельные конторы и предприятия для облегчения труда при вычислениях процентов разрабатывали свои особые таблицы, которые составляли коммерческий секрет компании.
Впервые опубликовал таблицы для расчета процентов в 1584 году Симон Стевин – инженер из города Брюгге (Нидерланды). Стевин известен замечательным разнообразием научных открытий в том числе – особой записи десятичных дробей.
Долгое время под процентами понимались исключительно прибыль и убыток на каждые 100 рублей. Они применялись только в торговых и денежных сделках. Затем область их применения расширилась, проценты встречаются в хозяйственных и финансовых расчетах, статистике, науке и технике. Нынче процент – это частный вид десятичных дробей, сотая доля целого (принимаемого за единицу).
Знак % происходит, как полагают, от итальянского слова cento (сто), которое в процентных расчетах часто писалось сокращенно cto. Отсюда путем дальнейшего упрощения в скорописи буква t превратилась в наклонную черту (/), возник современный символ для обозначения процента.
Характерно, что самая высокая и самая низкая процентные ставки были зарегистрированы в ХХ-м столетии. Так, в 20-х годах в Республики Германии процент по займу достигал в условиях гиперинфляции 10000% в год. Самая же низкая ставка была зарегистрирована в Нью-Йорке в период мирового экономического кризиса 30-х годов и составила 0,1% в год.
Использование процентов в повседневной жизни
40% алкоголя. В каждом литр жидкости составляет 0,4 литра алкоголя (и остальных других веществ)
15% рост цен. Новые цены превышают в 1,15 раза первоначальне; если ранее цена 100 крон, увеличение будет стоить 115 крон.
125% от средней. Учитывается параметр,который имеет значение числа, равное 1,25 средней стоимости; если в среднем по 200, этот параметр двести пятидесятый
10% людей. на каждые 100 человек приходится 10 человек, которые имеют ту или иную особенность
100% уверенности. Полная безопасность, отсутствие вероятности неудачи.
50%. 50/100 = 1/2 = половина
200%. 200/100 = двойная ставка
«Работать за проценты» — работать за вознаграждение, исчисляемое в зависимости от прибыли или оборота.
«На все сто (процентов)» — всецело, полностью, целиком.
«Процентщик» — человек, ссужающий деньги под большие проценты, ростовщик.
Типы задач на проценты
С процентами в основном решают такие типы задач:
— это задачи, в которых необходимо найти указанный процент от числа
— это задачи, в которых находится число по заданному другому числу и его величине в процентах от искомого числа
— и задачи, в которых надо найти процентное выражение одного числа от другого.
Расчеты процента
Процентное значение вычисляется путем умножения числового значения отношения 100. Например:
чтобы найти процент из 50 яблок из 1250 яблок, сначала вычислить соотношение 50/1250 = 0,04, а затем умножить на 100, чтобы получить 4%.
Чтобы вычислить процент, конвертировать проценты в долях 100, или десятичных знаков, и умножить их. Например, 50% 40%:
(50/100) х (40/100) = 0,50 Ч 0,40 = 0,20 = 20/100 = 20%.
Это не правильно разделить на 100 и использовать знак процента, в то же время. (Например, 25% = 25/100 = 0,25, а не 25% / 100, на самом деле (25/100) / 100 = 0,0025).
Самый простой способ вычислить того, в процентах (скидка 10% + 5%):
Например, если есть «10% + скидка 5%», общая скидка не 15%, но
Всякий раз, когда мы говорим о процентах, важно указать, что это относительно, то есть то, что общее, что соответствует 100%. Следующая задача иллюстрирует этот момент.
В известном колледже 60% всех студентов составляют женщины, а 10% всех студентов специальности информатика. Если 5% женщин, студентов специальности информатика, какой процент специальностей информатики составляют женщины?
Мы попросили вычислить соотношение женских специальностей информатики для всех специальностей информатики. Мы знаем, что 60% всех студентов составляют женщины, и среди них 5% составляют специальности информатика, поэтому мы заключаем, что (60/100) х (5/100) = 3/100 или 3% от общего числа студентов составляют женщины информатике специальностей. Разделив это 10% всех студентов, которые являются специальности компьютерные науки, мы приходим в ответ: 3% / 10% = 30/100 или 30% всех специальностей информатики составляют женщины.
Этот пример тесно связано с понятием условной вероятности.
Некоторые другие примеры процент изменения:
Увеличение на 800% означает, что итоговая сумма в 9 раз оригинал (100% + 800% = 900% = 9 раз больше).
В предыдущем примере, процентная ставка »увеличилась на 5 процентных пунктов» от 10% до 15%. Если скорость падает, то на 5 процентных пунктов, он вернется к первоначальной ставке 10%, как ожидалось.
Проценты в программировании
В Бейсике знак процента, поставленный сразу после имени переменной, означает тип данных «целое».
В языке Си знак процента обозначает операцию вычисления остатка от деления (8 % 3 == 2); также совместно с символами «d», «s» и некоторыми другими используется в строках задания формата ввода/вывода данных в соответствующих функциях.
В Perl знак процента, предшествующий имени переменной, означает тип данных «хэш».
В командах DOS и пакетных файлах используется как первый символ объявления подстановочной переменной для команды FOR; для пакетных файлов нужно указывать удвоенный символ процента — %%.
В системе Windows для доступа к переменным в консоли и bat файлах используется имя переменной заключённое между знаками процента, например, %u sername % покажет имя учётной записи, которой принадлежит запущенный процесс.
Применяется для замены символов, не входящих в ASCII, в строках URI в виде кодов типа %D0%9F%D1%80%D0%BE (первым стоит знак процента, потом двузначное шестнадцатеричное число).
В SQL знак процента при команде LIKE заменяет любое количество любых символов, то есть обеспечивает поиск по маске.
В Matlab-программах, LaTeX-разметке и PostScript знак процента употребляется перед началом строчного текстового комментария.
В калькуляторах имеется кнопка с изображением процента. В зависимости от организации изготовителя простейшие калькуляторы вычисляют:
— процентное отношение одного числа от другого;
— процентную надбавку (mark-up);
Источники
Википедия – Свободная энциклопедия, WikiPedia
slogos.ru – Понятие и определение
dic.academic.ru – Словарь Академика
mirurokov.ru – Математический словарь
Полезное
Смотреть что такое «Процент» в других словарях:
Процент — (interest) Плата, взимаемая за заем суммы денег. Процентная ставка (interest rate) есть плата, выраженная как процент от общей кредитуемой суммы, на определенный период времени, обычно на год. Так, процентная ставка, равная 15% ежегодно, означает … Финансовый словарь
ПРОЦЕНТ — (interest) Плата, взимаемая за кредит, помимо выплаты заимствованной суммы. Ставка процента является дополнительной оплатой за единицу ссуды; обычно рассчитывается в виде годовой ставки. Процентные ценные бумаги приносят доход владельцу;… … Экономический словарь
ПРОЦЕНТ — (лат.). Цифра, означающая прибыль или плату с сотни. В химии: выраженное в числах отношение различных составных частей вещества. В статистике: отношение народонаселения и т. д. Словарь иностранных слов, вошедших в состав русского языка. Чудинов А … Словарь иностранных слов русского языка
ПРОЦЕНТ — (interest) Плата, взимаемая за заем суммы денег. Процентная ставка (rate of interest) – плата, выраженная как процент от общей кредитуемой суммы на определенный период времени, обычно на год. Так, процентная ставка, равная 15% ежегодно, означает … Словарь бизнес-терминов
процент — — [[Англо русский словарь сокращений транспортно экспедиторских и коммерческих терминов и выражений ФИАТА]] процент Плата за пользование ссудным (заимствованным) капиталом во всех его формах (кредитный процент, депозитный процент, процент… … Справочник технического переводчика
Процент — (interest) плата за пользование ссудным (заимствованным) капиталом во всех его формах (кредитный процент, депозитный процент, процент по облигациям, процент по векселям и т.п.) … Экономико-математический словарь
процент — См … Словарь синонимов
ПРОЦЕНТ — (процент неправ.), процента, муж. (от лат. pro centum за сто). 1. Сотая доля какого нибудь числа, принимаемого за целое, единицу (обозначается знаком %). Правило процентов. 2. Количество кого чего нибудь, измеряемое в сотых долях чего нибудь,… … Толковый словарь Ушакова
ПРОЦЕНТ — муж. или проценты мн. счет или цифра, означающая доход или плату с сотни; рез, резы, настав (·стар.), соста, рост, росты, верхи, вершки, свершки, лихва. Казенные проценты, росты, кои платит казна, по смим долгам или займам; законные проценты, кои … Толковый словарь Даля
процент — (неправильно процент) … Словарь трудностей произношения и ударения в современном русском языке
ПРОЦЕНТ — (от лат. pro centum за сто) сотая доля числа; обозначается знаком %. Так, 3% от 18 есть 3 сотых от этого числа, т. е. 0,54. Проценты применяются в хозяйственных расчетах. Напр., вклад a рублей в сберегательном банке увеличивается на p % за год и… … Большой Энциклопедический словарь