Как называют деление в математике
Деление
В этом разделе познакомимся с делением и узнаем, что деление – это математическая операция, обратная умножению.
Умножение – это последовательное сложение чисел, а деление – это последовательное вычитание чисел.
Как ёжикам поделить между собой яблоки поровну?
Нужно воспользоваться действием деления и узнать, сколько раз по 3 содержится в 6.
Любой пример на умножение можно представить двумя примерами на деление.
Например, для выражения 6 • 4 = 24 есть два обратных выражения:
24 : 4 = 6 — нужно из 24 вычесть число 4 ровно 6 раз.
24 : 6 = 4 — нужно из 24 вычесть число 6 ровно 4 раз.
Числа при делении
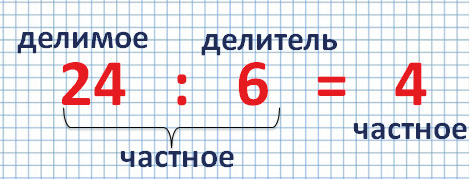
При делении, как и при другом математическом действии, каждое число имеет свое название.
Число, которое делят, называется делимое.
Число, на которое делят, называется делитель.
Результат деления называется частное.
Чтение числовых выражений
Этот пример можно прочитать по-разному.
Деление на 1
Деление на 0
Деление числа само на себя
Связь деления и умножения
Чётные и нечётные числа
Числа, которые делятся на 2 без остатка, называются чётными, а числа, которые не делятся на 2 без остатка, называются нечётными.
Чётные: 6, 22 44, 60, 74, 82, 96
Нечётные: 7, 13, 21, 37, 45, 97
В несколько раз меньше
Для примера решим задачу:
В магазине было 8 котят, а лисичек в 4 раза меньше. Сколько было лисичек?
Значит, чтобы узнать, сколько было лисичек, нужно 8 : 4 = 2 (л.)
Во сколько раз больше? Во сколько раз меньше?
Например, решим задачу: В магазине было 8 котят и 2 лисички. Во сколько раз котят было больше, чем лисичек? Во сколько раз лисичек было меньше, чем котят?
Чтобы ответить на эти вопросы, нужно узнать, сколько раз по 2 содержится в 8?
Значит, котят в 4 раза больше, чем лисичек, а лисичек в 4 раза меньше, чем котят.
Поделись с друзьями в социальных сетях:
Математика. 2 класс
Конспект урока
Математика, 2 класс
Урок № 55. Название чисел при делении
Перечень вопросов, рассматриваемых в теме:
1. Как называются числа при делении?
2. Как называется числовое выражение со знаком деление?
Обязательная литература и дополнительная литература:
Теоретический материал для самостоятельного изучения
Запишем равенство, используя необходимое арифметическое действие:
10 яблок разложили на две тарелки поровну.
9 конфет раздали трём детям поровну.
8 тетрадей раздали четырём ученикам поровну.
Для того, чтобы выполнит задание, нам понадобилось действие деление.
Вы уже знаете, как называются числа при сложении и вычитании, недавно вы познакомились с названиями чисел при умножении.
Вы умеете называть выражения со знаками «плюс», «минус», со знаком умножения. Сегодня вы узнаете, как называются числа при делении. Выражение со знаком деления тоже имеет своё название. Хотите узнать? Вперёд!
Числа при делении имеют свои названия.
8 листьев раздали детям, по 2 листа каждому.
4 человека получили листья.
Число, которое делят, называется делимым. 8 – это делимое. Число, на которое делят делимое, называется делитель. 2 – это делитель Результат действия деления называется частным. 4 – это частное. Выражение 8 разделить на 2 тоже называется частным.
Компоненты деления: делимое, делитель, частное.
Найдите частное, если делимое – 6, делитель – 3.
Найдите частное чисел 12 и 6. Проверьте: 12 : 6 = 2
Решим задачу: 12 клубничек раздали 4 детям поровну. По сколько клубничек получил каждый ребёнок?
Для решения задачи выберем действие деление, так как надо узнать, сколько раз по 4 содержится в числе 12.
Ответ: по 3 клубнички получил каждый ребёнок.
Вспомним название чисел при делении. 12 – делимое, 4 – делитель. 3 – частное. 12 : 4 – это частное.
Вывод: компоненты действия деление – делимое, делитель, результат деления – частное.
Ответим на вопросы, поставленные в начале урока.
Число, которое делят, называется делимое.
Число, на которое делят делимое, называется делитель.
Результат деления – частное.
Числа, которые соединены знаком деления, тоже называются частное.
Выполним несколько тренировочных заданий.
1. По рисунку составьте задачи на деление. Запишите решение. Назовите компоненты действия деление.
а) 15 яблок разложили в 3 вазы, в каждую вазу поровну. Сколько яблок положили в одну вазу?
Проверьте: 15 : 3 = 5 (яб.).
15 – делимое. 3 – делитель. 5 – частное. Выражение 15:3 – частное.
б) 15 яблок разложили в вазы, по 5 штук в каждую. Сколько ваз заняты яблоками?
15 – делимое. 5 – делитель. 3 – частное. Выражение 15:5 – частное.
2. Запишите выражение и найдите их значения:
Деление (математика)
Деле́ние (операция деления) — одно из четырёх простейших арифметических действий, обратное умножению. Деление — это такая операция, в результате которой получается число (частное), которое при умножении на делитель даёт делимое. Существует несколько символов, используемых для обозначения оператора деления.
Подобно тому, как умножение заменяет неоднократно повторенное сложение, деление заменяет неоднократно повторенное вычитание.
Рассмотрим, например, такой вопрос:
Сколько раз 3 содержится в 14?
Повторяя операцию вычитания 3 из 14, мы находим, что 3 «входит» в 14 четыре раза, и ещё «остаётся» число 2.
Результат деления также называют отношением.
Содержание
Деление натуральных чисел
Кольцо целых чисел не замкнуто относительно деления. Простым языком это означает то, что результат деления одного целого числа на другое может быть не целым. В случае, если всё-таки результат является целым числом, говорят о делении без остатка.
Деление чисел издавна считалось самой трудной из арифметических операций. В Средние века «секрет» деления знало не очень много посвящённых людей. Происходило это потому, что существовавшие алгоритмы деления были очень громоздки, сложны для исполнения и запоминания (например, деление в виде корабля (англ.) ). Появление деления столбиком радикально изменило эту ситуацию — теперь деление входит в раннюю школьную программу по математике наряду с остальными арифметическими действиями. Однако так же, как и в случае с умножением (см. быстрое умножение), в последнее время открыты более эффективные алгоритмы (см. en:Division (digital), применяющиеся в вычислительной технике.
Существуют правила, позволяющие быстро определить, делится ли число на заданный делитель без остатка (признаки делимости). Наиболее известные признаки делимости на 2, 3, 4, 5, 8, 9, 11, 25 и их производные, также существует признаки делимости на 7, 13, 1001 и другие числа.
Целое число, на которое одновременно делятся без остатка несколько чисел, называется их общим делителем.
Определение количества делителей натурального числа приводит к двум важным понятиям: составное и простое число. У простого числа есть ровно два различных делителя — 1 и само число. У составных чисел различных делителей больше двух. 1 не является ни составным, ни простым числом.
В случае, если одно натуральное число не делится на другое без остатка, можно говорить о делении с остатком. Рассмотрение остатков, их сравнение и формализация в виде вычетов привели к целой науке — теории чисел.
Обычно на остаток накладываются следующие ограничения (чтобы он был корректно, то есть однозначно, определён):


где 



Деление целых чисел
Деление произвольных целых чисел несущественно отличается от деления натуральных чисел — достаточно поделить их модули и учесть правило знаков.
Однако деление целых чисел с остатком определяется неоднозначно. В одном случае, (так же как и без остатка) рассматривают сначала модули и в результате остаток приобретает тот же знак, что делитель или делимое (например, 

Деление рациональных чисел
Замыкание множества целых чисел по операции деления приводит к расширению его до множества рациональных чисел. Это приводит к тому, что результатом деления одного целого числа на другое всегда является рациональное число. Более того, полученные числа (рациональные) уже полностью поддерживают операцию деления (замкнуты относительно неё).
Правило деления обыкновенных дробей:
Деление вещественных чисел
Деление также замкнуто в поле ненулевых вещественных чисел. Дедекиндово сечение позволяет однозначно определить результат деления.
Деление комплексных чисел
Комплексные числа опять замкнуты относительно операции деления.
Деление в алгебре
В отличие от простейших арифметических случаев на произвольных множествах и структурах деление может быть не только не определено, но и обладать множественностью результата.
Обычно в алгебре деление вводится через понятие единичного и обратного элементов. Если единичный элемент вводится однозначным образом (обычно аксиоматически или по определению), то обратный элемент часто может быть как левым (

К примеру, отношение матриц определяется через обратную матрицу, при этом даже для квадратных матриц может быть:

Отношение тензоров в общем случае не определено.
Деление многочленов
В общих чертах оно повторяет идеи деления натуральных чисел, ибо натуральное число есть не что иное, как значения многочлена, у которого коэффициенты — цифры, а вместо переменной стоит основание системы счисления:

Поэтому аналогично определяются: частное, делитель, делимое и остаток (с той лишь разницей, что ограничение накладывается на степень остатка). Поэтому к делению многочленов также применимо деление столбиком.
Отличие же заключается в том, что при делении многочленов основной упор делается на степени делимого и делителя, а не на коэффициенты. Поэтому обычно считается, что частное и делитель (а следовательно и остаток) определены с точностью до постоянного множителя.
Деление на ноль
По правилам стандартной арифметики деление на число 0 запрещено.
Другое дело — деление на бесконечно малую функцию или последовательность. Деление конечных функций на бесконечно малые приводит к появлению бесконечно больших, а отношение двух бесконечно малых называется неопределённостью 0/0, которую можно преобразовать (см. раскрытие неопределённостей) с тем, чтобы получить определённый результат.
Операции деления ненулевого числа на ноль не соответствует никакое действительное число.
Результат этой операции считается бесконечно большим и равным бесконечности: 

Смысл этого выражения состоит в том, что если делитель приближается к нулю, а делимое остается равным a или приближается к нему, то частное неограниченно увеличивается(по модулю).
Деление чисел
Деление — это арифметическое действие, с помощью которого можно узнать, сколько раз одно число содержится в другом.
Деление можно представить, как неоднократно повторяемое вычитание. Например, число 6 разделить на 2 — значит узнать, сколько раз число 2 содержится в 6:
Повторив вычитание 2 из 6, мы узнали, что 2 содержится в 6 три раза. Это можно проверить сложив три раза по 2 или умножив 2 на 3:
Для записи деления используется знак : (двоеточие), который ставится между числами. Например:
Эта запись означает, что 6 надо разделить на 2. Справа от записи деления ставится знак = (равно), после которого записывается полученный результат:
Задача. В магазин привезли 9 морковок. Продавщица связала их в пучки по 3 морковки в каждом пучке. Сколько получилось пучков?
Решение: Чтобы решить эту задачу, надо узнать, сколько раз по 3 содержится в числе 9. Для этого разделим 9 на 3. Получим 3.
Решение можно записать так:
Пример. Решить примеры на деление с помощью схем.
2) 12 : 4 = 3, 12: 3 = 4.
Делимое, делитель и частное
Делимое — это число, которое делят. Делитель — это число, на которое делят. Например, в записи:
12 — это делимое, 3 — делитель. Делитель показывает на сколько равных частей нужно разделить делимое.
Частное — это число, которое получается в результате деления. Например, в записи:
4 — это частное. При этом сама запись 12 : 3 тоже называется частным.
Проверка деления
где 28 — это делимое, 4 — это делитель, а 7 — частное. Чтобы узнать правильно ли было выполнено деление, можно:
или умножить делитель на частное:
Общее представление о делении натуральных чисел
В рамках этого материала мы разберем важное действие, называемое делением. Дав общее представление о нем и объяснив его смысл, мы введем основные термины и обозначения на письме. В последнем пункте мы расскажем, для решения каких задач нам пригодится умение делить натуральные числа.
Что такое деление натуральных чисел
Само по себе понятие деление неразрывно связано с процессом разъединения некоторого множества предметов на несколько отдельных множеств.
Объясним на примере.
В быту мы часто употребляем слова»делиться», «поделиться», например, поделиться угощением с друзьями. Это слово означает, что угощение мы поделили на некоторые части и отдали часть одним людям, а часть другим (или оставили себе). С помощью этого простого примера деление можно представить как последовательное вычитание из одного большого множества. Что такое вычитание и как его выполнять, мы уже разбирали с вами ранее.
Основной смысл процесса деления
На основе того, что мы озвучили, можно придать определенный смысл делению одного натурального числа на другое (отдельно выделим число, которое делят, и то, на которое делят). Мы помним, что понятие натуральных чисел проще всего соотнести с количеством некоторых предметов. То число, которое необходимо поделить, выражает число предметов исходного множества. В зависимости от того, какой смысл мы придаем второму числу (т.е. тому, на которое делят), можно выделить два основных подхода к пониманию смысла деления. Возможны такие варианты:
Разделить одно натуральное число на другое без остатка возможно далеко не всегда. Так, 10 конфет мы можем ровно разделить на 2 или 5 кучек, а на 3 нет, потому что в одном из множеств окажется отличное от других число конфет. Разложить 10 конфет по 15 или 20 кучкам мы также не в состоянии. Смысл таких действий объясняется в материале про деление с остатком.
Если мы можем поделить одно натуральное число на другое, то получившееся в итоге число также будет натуральным.
Основные понятия процесса деления
В этом пункте мы укажем основные обозначения и понятия, используемые в делении натуральных чисел.
Чтобы обозначить деление в записи, обычно используют знак двоеточия: « : ». Иногда можно встретить вместо него знак « ÷ », который означает то же самое. Первым мы записываем число, которое будем делить, потом знак деления, а потом число, на которое делим. Числовое выражение вида 10 : 5 означает, что мы делим десять на пять.
То число, которое делим, называем делимым. То, на которое делим – делителем. Итог вычислений правильно называть частным. Само числовое выражение, состоящее из делимого, делителя и знака деления, тоже называется частным.
Когда мы говорим о том, что нужно определить число, являющееся результатом деления одного натурального числа на другое, нужно использовать выражения «найти частное» или «вычислить частное».
Запись читается как «тридцать разделить на шесть равно пяти» или «частное от деления тридцати на шесть равно пяти».
Схематично процесс деления можно отобразить как » делимое : делитель = частное.».
Задачи с применением деления
Приведем примеры задач, для которых нужно уметь делить одно натуральное число на другое.
1. Первый тип задач – это те, в которых нужно найти, сколько множеств получится после деления исходного множества на равные части, а также близкие к ним задачи на вычисление количества предметов в каждом множестве после деления. Ранее мы уже приводили примеры таких задач. Добавим еще несколько.
Допустим, у нас есть 40 ручек, которые нужно распределить поровну между 4 коробками. Как вычислить, сколько ручек положить в каждую из них?
Ответ: 10
На ужин было приготовлено 12 котлет. Каждому члену семьи должно достаться по две. Сколько всего человек будут ужинать?
2. Второй тип задач очень схож с первым, однако в них необходимо вычислить не количество предметов, а изменения физических величин (времени, температуры, длины и др.)
Например, у нас есть полная бочка молока объемом 100 л. Сколько надо взять двухлитровых бутылок, чтобы перелить туда все имеющееся молоко?
Ответ: 100
Ответ: 3
3. Третий тип задач – это те, где нужно найти, во сколько раз уменьшилось исходное количество чего-либо, или выяснить, во сколько одно множество предметов или величина больше, чем другое. Например:
Планировалось построить дом площадью 120 кв м., но в итоге построили в два раза меньше. Какую площадь имеет в итоге построенный дом?
Ответ: 60