Как называют числа при сложении
Сложение
Познакомимся со сложением.
Рассмотрим числовой ряд.
Числа идут слева направо, по порядку, как при счёте.
0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10
Посмотри на числовой ряд, по которому идёт заяц.
Какое действие выполняет заяц?
Прибавляет число 2.
К какому числу он прибавляет число 2?
К числу 4.
Наш зайчик стоит на числе 4 и думает, в какую сторону ему идти.
В какую сторону пойдёт зайчик?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает заяц?
2, потому что ему нужно прибавить 2.
На каком делении остановится заяц?
На числе 6.
Когда прибавляем, становится больше.
Чем правее, тем числа больше.
4 + 2 = 6
Рассмотрим еще один пример.
Какое действие выполняет заяц?
Прибавляет число 5.
К какому числу он прибавляет число 5?
К числу 3. Мы поставили зайчика на число 3.
В какую сторону он пойдёт?
Вправо, потому что у него на табличке знак +.
Сколько шагов вправо сделает зайчик? 5.
На каком делении он остановится? На числе 8.
3 + 5 = 8
Как называются числа при сложении?
Первое слагаемое и второе слагаемое.
Результат называется суммой.
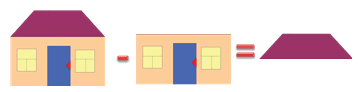
Представь части домика как слагаемые и сумму.
Как найти неизвестное слагаемое
Второе слагаемое неизвестно.
Рассмотри рисунок и догадайся, как его можно найти.
Нужно из суммы вычесть первое слагаемое.
Неизвестно первое слагаемое.
Как его можно найти?
Нужно из суммы вычесть второе слагаемое.
Чтобы найти неизвестное слагаемое, нужно из суммы вычесть известное слагаемое.
Проверка сложения
Если из суммы двух слагаемых, вычесть одно из слагаемых, то получится второе слагаемое.
Именно эта связь между суммой и слагаемыми используют для проверки вычислений.
Например, 35 + 7 = 42.
Правильно ли произведено вычисление? Можно проверить так:
Перестановка слагаемых
Сделаем запись к рисунку.
3 + 2 = 5
Сделаем запись к этому рисунку.
2 + 3 = 5
Теперь рассмотрим обе записи к рисункам:
3 + 2 = 5
2 + 3 = 5
Мы заметили, что сумма в обеих записях одинаковая, хотя слагаемые мы записывали по-разному.
Это переместительный закон сложения, который гласит:
От перестановки мест слагаемых сумма не меняется.
Сочетательный закон сложения
1) Какие числа удобно сложить сначала, чтобы получился удобный способ? Числа 29 и 1.
Сумму чисел 29 и 1 возьмем в скобки.
37 + (29 + 1) = … (читаем: к 37 прибавить сумму чисел 29 и 1)
Решаем. Сначала выполним действие в скобках.
Вывод: два соседних слагаемых можно заменить их суммой.
Поделись с друзьями в социальных сетях:
Сложение натуральных чисел
Пройти тест по теме «Сложение и вычитание натуральных чисел» можно по ссылке. Проверьте свои знания!
Сумма чисел – это такое число, которое получается после объединения всех единиц других данных натуральных чисел.
Слагаемые – это числа, над которыми мы выполняем действие сложения. Иными словами, это те числа, количество единиц которых мы объединяем в новом числе.
Арифметическое действие – это нахождение нового числа при помощи двух или нескольких других данных чисел.
В курсе математики 5 класса изучаются основные арифметические действия – сложение, вычитание, умножение и деление.
Сложение – это арифметическое действие, которое выполняется для получения суммы нескольких чисел.
Или другими словами:
Сложение – это действие увеличения числа на количество единиц, содержащихся в другом числе.
Сумма – это результат действия сложения.
Компоненты действия сложения для двух слагаемых:
Компоненты сложения для трех слагаемых:
Рисунок 1. Сумма двух чисел на координатном луче.
Основные свойства суммы натуральных чисел
Переместительный закон сложения
Сумма двух или нескольких чисел от изменения порядка сложения слагаемых не меняется.
Это значит, что значение суммы не зависит от порядка выполнения действия сложение.
Сочетательный закон сложения
Сумма нескольких чисел не поменяется, если некоторые слагаемые заменить их суммой.
Это значит, что мы можем группировать слагаемые как угодно, а также выполнять действия сложения в любом порядке.
Например, если в нашем примере мы заменим слагаемые 2 и 3 их суммой, то результат останется такой же, как и при обычном сложении слагаемых:
или
или
Для прибавления суммы некоторых чисел к числу или некоторого числа к сумме чисел, нужно сложить это число с одним из слагаемых суммы, а получившийся результат сложить последовательно с остальными слагаемыми.
Пример 1. Прибавление числа к сумме чисел:
Можно сразу вычислить сумму чисел в скобках и сложить ее с первым слагаемым:
325 +( 12 + 64 + 5 ) = 325 +81 = 406
Также можно использовать правило прибавления слагаемого и суммы. Результат при этом не поменяется
Пример 2. Прибавление суммы чисел к другому числу:
Можно сразу вычислить сумму чисел в скобках и сложить ее со вторым слагаемым
( 54 + 240 + 189 )+ 37 = 483+ 37 = 520
Или можно использовать правило прибавления суммы чисел к числу. Результат останется тот же.
Изменение суммы чисел с изменением слагаемых
При увеличении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже увеличится на это же число (на это же количество единиц).
При уменьшении одного из слагаемых на какое-то число (на какое-то количество единиц), сумма тоже уменьшится на это же число (на это же количество единиц).
Эти два свойства справедливы и в обратную сторону. То есть, если увеличить или уменьшить сумму на какое-то число, тогда для сохранения равенства нужно соответственно увеличить или уменьшить одно из слагаемых.
Простой пример увеличения суммы при увеличении слагаемого: у вас есть 700 рублей; 200 рублей лежит в левом кармане, а 500 – в правом. Вы нашли на улице 300 рублей и положили их в левый карман, после чего там стало 200+300=500 рублей. Таким образом, всего у вас оказалось 500+500=1000 рублей, то есть, сумма всех ваших денег увеличилась на 300 рублей.
Попробуйте самостоятельно придумать примеры для всех трех правил.
Сложение однозначных чисел
Сложение двух однозначных чисел выполняется так: одно число увеличивается на количество единиц другого числа. То есть, единицы одного числа присоединяются к единицам другого числа.
Сложение многозначного числа с однозначным
Чтобы найти сумму многозначного числа и однозначного, можно действовать двумя способами. Оба они основаны на свойствах суммы чисел. Рассмотрим их на примерах.
То есть, мы проделываем такие действия:
88+5 = 80+8+5 = 80+13 = 80+10+3 = 90+3=93.
То есть, ход вычисления был такой:
88+5 = 88+2+3 = 90+3 = 93.
Сложение в столбик многозначных чисел
Сложение в столбик – это способ нахождения суммы чисел путем их записи друг под другом таким образом, чтобы соответствующие разряды разных чисел находились на одной вертикали (один под другим).
Итак, допустим, что нам нужно найти сумму : 5728+803
После нахождения суммы чисел методом сложения столбиком, записываем результат решения в исходном строчном примере:
5728+803 = 6531
Сложение в столбик нескольких многозначных чисел
Рассмотрим пример: 12044+28609+1358
Сложив простые единицы, мы получим 21, то есть, 2 десятка и 1 единицу. Записываем под чертой в разряде единиц цифру 1, а 2 отмечаем «в уме».
Нам остается только записать результат в начальном примере:
12044+28609+1358
 shymchuknp
shymchuknp
Учитель начальных классов
Шимчук Наталья Петровна
2 класс. Математика. Названия чисел при сложении и вычитании
ТЕМА: Названия чисел при сложении и вычитании. Переместительное свойство сложения. Сложение и вычитание чисел частями. Сложение и вычитание двузначных чисел без перехода через разряд. Задачи на нахождение суммы и остатка, на разностное сравнение. Сравнение чисел. Единицы измерения длины. Сравнение длин отрезков.
Вспомним изученный материал: прочитай и расскажи.
· Числа, используемые при счете предметов, называются натуральными.
· В записи двузначного числа цифра справа обозначает единицы, цифра слева – десятки.
· Памятка для поразрядного сравнения чисел
1. Сравниваю числа десятков : больше то число, в котором десятков больше; меньше то, в котором десятков меньше.
2. Если десятков поровну, то сравниваю числа единиц : больше то число, в котором единиц больше, меньше то, в котором единиц меньше.
· Числа при сложении: первое слагаемое, второе слагаемое, сумма
· Переместительный закон сложения: от перестановки мест слагаемых, сумма не изменяется.
· Числа при вычитании: уменьшаемое, вычитаемое, разность
· Составные части задачи:
2. Числовые данные, искомое
3. Краткая запись, схема
· Рассуждай так: Чтобы ответить на вопрос задачи, достаточно знать два числовых значения. На вопрос задачи ответим арифметическим действием …..(сложением или вычитанием)
· Задачи на разностное сравнение – вопрос задачи звучит так: На сколько больше (меньше) ….
Приступим к практической части.
1) Запиши дату, Классная работа
9 12 4 33 0 7 19 74 5 83 68
3) Замени числа суммой разрядных слагаемых: 13, 24, 65, 11, 28, 87
4) Вспомни состав чисел 2 – 10.
5) Запиши числа 7-го десятка.
6) Запиши числа, содержащие 5 единиц
7) Вставь такие цифры, чтобы получились истинные равенства.
8) Сравни числа. На сколько число больше? Меньше?
20 ….. 40 на …. 8….. 10 на ….
9) Работа по учебнику: № 15, 17, 24, 25, 38, 40
Сложение
Сложение (прибавление) — одна из основных операций (действий) в разных разделах математики, позволяющая объединить два объекта (в простейшем случае — два числа). Более строго сложение — бинарная операция, определённая на некотором множестве, элементы которого мы будем называть числами, при которой двум числовым аргументам (слагаемым) a и b сопоставляется итог (сумма), обычно обозначаемый с помощью знака «плюс»: a+b.
Содержание
Определение сложения
Абстрактная алгебра
В абстрактной алгебре сложением может называться любая бинарная, коммутативная и ассоциативная операция. В случае, если на этом множестве определено также умножение, то сложение предполагается дистрибутивным по отношению к нему.
Свойства сложения в арифметике
Сложение обладает следующими свойствами:
В других системах (чисел, объектов) любое из этих свойств может не выполняться.
Обозначение операции
Знак плюс для операции сложения плюса (а также знак минуса) придумали в немецкой математической школе «коссистов» (то есть алгебраистов). Они используются в «Арифметике» Иоганна Видмана, изданной в 1489 году. До этого сложение обозначалось буквой p (plus) или латинским словом et (союз «и»), а вычитание — буквой m (minus). У Видмана символ плюса заменяет не только сложение, но и союз «и». Происхождение этих символов неясно, но, скорее всего, они ранее использовались в торговом деле как признаки прибыли и убытка. Оба символа вскоре получили общее распространение в Европе — за исключением Италии, которая ещё около века использовала старые обозначения.
Запись при помощи буквы Σ
См. также
Полезное
Смотреть что такое «Сложение» в других словарях:
СЛОЖЕНИЕ — СЛОЖЕНИЕ, сложения, ср. 1. только ед. Действие по гл. сложить во 2, 5 и 7 знач. складывать слагать. Сложение сил (замена нескольких сил одной, производящей равноценное действие; физ.). Сложение величин. Сложение обязанностей. 2. только ед. Одно… … Толковый словарь Ушакова
сложение — См … Словарь синонимов
СЛОЖЕНИЕ — СЛОЖЕНИЕ, сложить, сложный и пр. см. слагать. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
СЛОЖЕНИЕ — одно из четырёх арифметических действий, с помощью которого по двум заданным числам а и b (слагаемым) находят третье число с (сумма, результат), которое обозначают как а + b. При сложении справедливы законы: переместительный (коммутативный) a + b … Большая политехническая энциклопедия
СЛОЖЕНИЕ — арифметическое Действие. Обозначается знаком + (плюс). В области целых положительных чисел (натуральных чисел) в результате сложения по данным числам (слагаемым) находится новое число (сумма), содержащее столько единиц, сколько их содержится во… … Большой Энциклопедический словарь
СЛОЖЕНИЕ — СЛОЖЕНИЕ, арифметическая операция, обозначаемая знаком + (плюс). Ее называют ДВОИЧНОЙ ОПЕРАЦИЕЙ, поскольку для того, чтобы операция имела смысл, необходимы по меньшей мере два числа (или элемента) … Научно-технический энциклопедический словарь
сложение — СЛОЖЕНИЕ, я, ср. 1. см. сложить. 2. Математическое действие, посредством к рого из двух или нескольких чисел (или величин) получают новое, содержащее столько единиц (или величин), сколько было во всех данных числах (величинах) вместе. Задача на с … Толковый словарь Ожегова
СЛОЖЕНИЕ 1 — СЛОЖЕНИЕ 1, я, ср. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
СЛОЖЕНИЕ 2 — СЛОЖЕНИЕ 2, я, ср. То же, что телосложение. Богатырское с. Толковый словарь Ожегова. С.И. Ожегов, Н.Ю. Шведова. 1949 1992 … Толковый словарь Ожегова
сложение — — [А.С.Гольдберг. Англо русский энергетический словарь. 2006 г.] Тематики энергетика в целом EN addition … Справочник технического переводчика
Название чисел при сложении (слагаемые, сумма)
«Управление общеобразовательной организацией:
новые тенденции и современные технологии»
Свидетельство и скидка на обучение каждому участнику
Технологическая карта урока
Технология проблемно-диалогического обучения, здоровьесберегающая технология
Способствовать развитию связной речи, оперативной памяти, произвольного внимания.
Создать условия для воспитания уважения к чужому мнению, доброжелательного отношения друг к другу, чувства взаимопомощи, сознательного отношения к учёбе и к изучению предмета.
Цели учебной деятельности
-Познакомить с терминами «слагаемое», «сумма»;
-научить читать равенства, используя математическую терминологию ( слагаемое и сумма);
— развивать логическое мышление, внимание, коммуникативные качества.
умений прибавлять и вычитать число 2;
— создать условия для усвоения математических понятий «слагаемые, сумма»;
— закрепить умение называть числа при сложении;
— Развивать познавательный интерес.
-Развивать умение рассуждать, делать выводы.
-Способствовать развитию мышления, произвольного внимания.
-Формировать навыки саморегуляции.
— Воспитывать аккуратность и умение помочь товарищу.
— Воспитывать культуру поведения при фронтальной и индивидуальной работе.
Интерактивный комплекс, презентация, диск «Математика», учебник «Математика»
Обучающие и развивающие компоненты, задания и упражнения
1.Организационный момент. Психологический настрой.
Эмоциональный настрой на урок. Проверка готовности оборудования и класса к уроку.
Учитель спросит – надо встать.
Когда он сесть позволит – сядь.
Ответить хочешь – не шуми,
А лучше руку подними.
Проверка готовности к уроку.
Приветствуют учителя. Организуют своё рабочее место, проверяют наличие индивидуальных принадлежностей.
Проявляют эмоциональную отзывчивость на слова учителя.
Фронтальный. Наблюдение учителя.
2. Актуализация опорных знаний.
– Расположите все вагончики в порядке возрастания результатов.
• Стоя на одной ноге, гусь весит 2 кг. Сколько он будет весить, стоя на двух ногах? (2 кг.)
• Вова за 1 ч поймал 5 рыбок. Сколько рыбок он поймает за 2 ч? (Нельзя ответить.)
• Шли 2 друга в школу. Навстречу им шли еще 2 друга. Сколько друзей шло в школу? (2.)
Учитель кидает мяч и говорит вопрос или задание.
• Какое число на 2 меньше, чем 8? (6.)
• Какое число больше 5 на 2? (7.)
По цепочке у доски выставляют вагончики в порядке возрастания результатов.
Решают задачи устно.
Отвечает тот, кто поймал мяч.
Закрепление умений прибавлять и вычитать число 2.
Учатся самостоятельно планировать и выполнять свои действия на знакомом учебном материале; выполнять действия в сотрудничестве с учителем по предложенному плану.
Фронтальный. Устные ответы
Принятие целей учебно- познавательной деятельности.
Ай да белка-мастерица!
Вяжет детям рукавицы.
Извязала три клубка,
Два еще лежат пока.
У кого ответ готов:
Сколько у нее клубков? (5.)
— Как вы узнали? (3 + 2 = 5.)
— Как можно эту запись прочитать по-разному?
— Можно ли по-другому прочитать запись?
На этот вопрос вы сможете ответить в конце урока.
– Сегодня на уроке мы подробно рассмотрим ту группу, где выполняется действие «сложение».
Учащиеся слушают учителя, отвечают на вопрос: К 3 прибавить 2 — получится 5, 3 увеличить на 2 — получится 5, 3 еще 2 —будет 5.
Учатся принимать и выполнять учебную задачу.
Фронтальный. Наблюдение учителя.
4 . Усвоение знаний и способов действий.
Объяснение новых понятий.
После этого учитель вывешивает на доску таблицу :
Название чисел при сложении
Учитель тренирует учеников в чтении примеров с использованием терминов «слагаемое», «сумма».
Например: первое слагаемое – 4, второе слагаемое – 2, сумма равна 6. Сумма чисел 5 и 2 равна 7.
Учителем проводится отработка с учащимися использования терминов «первое слагаемое», «второе слагаемое», «сумма чисел».
– Можно ли примеры на вычитание читать, используя слова «слагаемое», «сумма»? (Нет.)
Учащиеся запоминают названия компонентов и результатов действия сложения.
Формулировать и удерживать учебную задачу, преобразовывать практическую задачу в познавательную: знать название чисел при сложении.
Фронтальный. Наблюдение учителя.
Интерактивная физминутка «Буратино»
— Предлагает отдохнуть, принять активное участие в физминутке.
Выполняют предложенные движения . Ориентируясь на здоровый образ жизни, активно участвуют в физминутке.
Осуществлять профилактику утомления.
Коллективный. Наблюдение учителя.
6. Закрепление знаний и способов действий.
Формирование навыков счёта.
Работа по учебнику №2 (с. 86)
Пропедевтика темы «Задача».
Работа в тетради с печатной основой .
Учитель предлагает выполнить примеры, обращает внимание детей на то, чтобы они при комментировании читали выражения по-разному.
Учитель предлагает хорошо читающему ученику прочитать задачу.
– О чем прочитанный рассказ? Что в рассказе известно?
– Какое арифметическое действие следует выполнить, чтобы ответить на поставленный вопрос?
— Почему так считаете?
Аналогично разбирается задача.
Учитель предлагает выполнить задание на закрепление умения прибавлять и вычитать число 2.
— Откройте тетрадь. Прочитайте первое задание.
— Что такое слагаемые? (Числа, которые складываем.)
— Какие равенства подчеркнули? Прочитайте их с ответом.
— Прочитайте следующее задание. Выполните его.
— Какое равенство составили к первому рисунку? (5 + 7 = 6.)
— Какое равенство составили ко второму рисунку? (7— 1 = 6.)
— Составьте рассказы по рисункам.
Один из учащихся читает задачу. Учащиеся отвечают на вопросы:
-Известно, что у Васи было 6 книг и ему подарили ещё 2 книги.
-Сколько книг стало у Васи.
-Потому что книг у Васи стало больше.
Далее ученики записывают с комментированием решение задачи: 6 + 2 = 8 (кн.).
Учащиеся объясняют, кто из сказочных героев ошибся. (Ошибся заяц, так как он должен был выполнить действие «сложение», при сложении число увеличивается, то есть заяц должен был сделать два шага вперёд, а не назад.)
Учащиеся выполняют задания под руководством учителя, отвечая на поставленные вопросы.
Остальные задания учащиеся выполняют самостоятельно. Самооценка с помощью «Светофора».
Формируются умения прибавлять и вычитать число 2; знать название чисел при сложении.
Умение стремиться к расширению своей познавательной сферы, стараться производить логические мыслительные операции (анализ, сравнение) для решения познавательной задачи.
Необходимые умения к изучению темы «Задача» (анализ, синтез, мышление)
Умение самостоятельно планировать и выполнять свои действия на знакомом учебном материале; выполнять действия в сотрудничестве с учителем по предложенному плану; самостоятельно выстраивать план действий по решению учебной задачи изученного вида.
Наблюдение учителя, работы в тетради.
Обобщение и оценка.
— А теперь время подвести итоги. Мы плодотворно поработали.
— Что нового узнали на уроке? Как называются числа, которые складываются?
-Как называется результат, полученный при сложении?
Оцените себя с помощью «Светофора»
Учащиеся отвечают на вопросы.
Выбирают сигнальную карточку, которая соответствует оценке работы на уроке.
Уметь с достаточной полнотой и точностью выражать свои мысли.
Давать эмоциональную оценку деятельности на уроке.
Наблюдение учителя Самоконтроль и самооценка
Курс повышения квалификации
Дистанционное обучение как современный формат преподавания
Курс повышения квалификации
Скоростное чтение
Курс повышения квалификации
Актуальные вопросы теории и методики преподавания в начальной школе в соответствии с ФГОС НОО
Ищем педагогов в команду «Инфоурок»
Номер материала: ДБ-228911
Не нашли то, что искали?
Вам будут интересны эти курсы:
Оставьте свой комментарий
Авторизуйтесь, чтобы задавать вопросы.
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
В России разработают рекомендации по сопровождению студентов с ОВЗ
Время чтения: 2 минуты
Учителя о ЕГЭ: секреты успешной подготовки
Время чтения: 11 минут
Все школы РФ с 2023 года подключат к государственной информационной системе «Моя школа»
Время чтения: 1 минута
В Минпросвещения рассказали о формате обучения школьников после праздников
Время чтения: 1 минута
Минпросвещения создает цифровую психологическую службу для школьников
Время чтения: 1 минута
Во всех педвузах страны появятся технопарки
Время чтения: 1 минута
Подарочные сертификаты
Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.
Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.








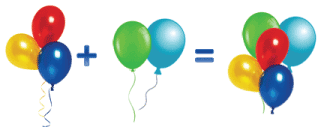
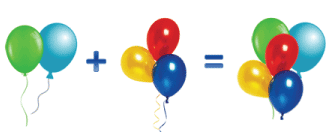






















 shymchuknp
shymchuknp





