Как называется запятая в математике
Десятичная запятая
Имеет особую форму записи: целая часть в десятичной системе счисления, затем запятая и затем дробная часть в десятичной системе счисления, причём количество цифр дробной части строго определяется размерностью дробной части: если это десятые доли, дробная часть записывается одной цифрой; если тысячные — тремя; десятитысячные — четырьмя и т. д.
| обыкновенная дробь | десятичная дробь |
|---|---|
| 4 /10 | 0,4 |
| 79 395 /1000 | 79,395 |
Очевидно, в начало целой части и/или в конец дробной части можно дописывать сколько угодно нулей.
Существуют также бесконечные десятичные дроби — периодические и непериодические. Например, ⅓ записывается как бесконечная периодическая дробь 0,3333… или 0,(3). А число π записывается как бесконечная непериодическая дробь 3,141592…
Периодическая десятичная дробь называется чистой периодической дробью, если её период (группа повторяющихся цифр) начинается сразу после запятой, а период может содержать любое конечное число цифр. Так, дробь 1,(3) — чистая периодическая дробь. Если периодическая десятичная дробь содержит ещё число, заключённое между целой частью и периодом, то такая периодическая дробь называется смешанной; число периодической дроби, стоящее между целой частью и периодом, называется предпериодом этой дроби.
Очевидно, что всякая периодическая дробь является рациональным числом вида 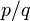
Произношение десятичных дробей
В русском языке десятичные дроби читаются так: сначала произносится целая часть, потом слово «целых» («целая»), потом десятичная часть так, как если бы всё число состояло только из этой части, то есть числитель дроби — количественное числительное женского рода (одна, две, восемь и т. д.), а знаменатель — порядковое числительное (седьмая, сотая, двести тридцатая и т. д.).
Однако на практике часто встречается такое произношение: целая часть, союз «и», дробная часть.
Десятичные дроби
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Понятие десятичной дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это запись числа в математика, в которой a и b — числа или выражения. По сути, это всего лишь одна из форм, в которое можно представить число. Есть два формата записи:
В обыкновенной дроби над чертой принято писать делимое, которое становится числителем, а под чертой всегда находится делитель, который называют знаменателем. Черта между числителем и знаменателем означает деление.
В десятичной дроби знаменатель всегда равен 10, 100, 1000, 10000 и т.д. По сути, десятичная дробь — это то, что получается, если разделить числитель на знаменатель. Десятичную дробь записывают в строчку через запятую, чтобы отделить целую часть от дробной. Вот так:
Конечная десятичная дробь — это дробь, в которой количество цифр после запятой точно определено.
Бесконечная десятичная дробь — это когда после запятой количество цифр бесконечно. Для удобства математики договорились округлять эти цифры до 1-3 после запятой.
Свойства десятичных дробей
Главное свойство десятичной дроби звучит так: если к десятичной дроби справа приписать один или несколько нулей — ее величина не изменится. Это значит, что если в вашей дроби куча нулей — их можно просто отбросить. Например:
Обыкновенная и десятичная дробь — давние друзья. Вот, как они связаны:
Обучение на курсах по математике — отличный способ закрепить полученные знания на практике и подтянуть сложные темы.
Как записать десятичную дробь
Давайте разберем на примерах, как записывается десятичная дробь. Небольшая напоминалка: сначала пишем целую часть, ставим запятую и после записываем числитель дробной части.
Пример 1. Перевести обыкновенную дробь 16/10 в десятичную.
Пример 2. Перевести 37/1000 в десятичную дробь.
Ответ: 37/1000 = 0,037.
Как читать десятичную дробь
Чтобы учитель вас правильно понял, важно читать десятичные дроби грамотно. Сначала произносим целую часть с добавлением слова «целых», а потом дробную с обозначением разряда — он зависит от количества цифр после запятой:
| Сколько цифр после запятой? | Читается, как |
|---|---|
| одна цифра — десятых; | 1,3 — одна целая, три десятых; |
| две цифры — сотых | 2,22 — две целых, двадцать две сотых; |
| три цифры — тысячных; | 23,885 — двадцать три целых, восемьсот восемьдесят пять тысячных; |
| четыре цифры — десятитысячных; | 0,5712 — ноль целых пять тысяч семьсот двенадцать десятитысячных; |
| и т.д. |
Сохраняй наглядную картинку, чтобы быстрее запомнить.
Преобразование десятичных дробей
Чтобы ни одна задача не смутила вас своей формулировкой, важно знать, как преобразовывать десятичные дроби в другие виды. Сейчас научимся!
Как перевести десятичную дробь в проценты
Уже в пятом классе задачки по математике намекают, что дроби как-то связаны с процентами. И это правда: процент — это одна сотая часть от любого числа, обозначают его значком %.
Чтобы узнать, как перевести проценты в дробь, нужно убрать знак % и разделить наше число на 100, как в примере выше.
А чтобы перевести десятичную дробь в проценты — умножаем дробь на 100 и добавляем знак %. Давайте на примере:
Выразить дробь в процентах просто: сначала превратим её в десятичную дробь, а потом применим предыдущее правило.
2/5 = 0,4
0,4 · 100% = 40%
8/25 = 0,32
0,32 · 100% = 32%
Чтобы разрезать торт на равные кусочки и не обижать гостей, нужно всего-то запомнить соотношения частей и целого. Наглядная табличка — наш друг-помощник:
Преобразование десятичных дробей
Десятичная дробь — это число с остатком, где остаток стоит после целой части и разделяется запятой.
Смешанная дробь — это тоже число с остатком, но остаток записывают в виде простой дроби (с черточкой).
Чтобы переводить десятичные дроби в смешанные, не нужно запоминать особые алгоритмы. Достаточно понимать определения и правильно читать заданную дробь — этим школьники и занимаются в 5 классе. А теперь давайте потренируемся!
Пример 1. Перевести 5,4 в смешанное число.
Пример 2. Перевести 4,005 в смешанное число.
Ответ: 4,005 = 4 1/200.
Пример 3. Перевести 5,60 в смешанное число.
Как перевести десятичную дробь в обыкновенную
Не будем придумывать велосипед и рассмотрим самый простой способ превращения десятичной дроби в обыкновенную. Вот, как это сделать:
Не забывайте про минус в ответе, если пример был про отрицательное число. Очень обидная ошибка!
Действия с десятичными дробями
С десятичными дробями можно производить те же действия, что и с любыми другими числами. Рассмотрим самые распространенные на простых примерах.
Как разделить десятичную дробь на натуральное число
Пример 2. Разделить 183,06 на 45.
Ответ: 183,06 : 45 = 4,068.
Как разделить десятичную дробь на обыкновенную
Чтобы разделить десятичную дробь на обыкновенную или смешанную, нужно представить десятичную дробь в виде обыкновенной, а смешанное число записать, как неправильную дробь.
Пример 1. Разделить 0,25 на 3/4.
Пример 2. Разделить 2,55 на 1 1/3.
Ответ: 2,55 : 1 1/3 = 1 73/80.
Как умножить десятичную дробь на обыкновенную
Чтобы умножить десятичную дробь на обыкновенную или смешанную, используют два правила за 6 класс. При первом приводим десятичную дробь к виду обыкновенной и потом умножаем на нужное число. Во втором случае приводим обыкновенную или смешанную дробь в десятичную и потом умножаем.
Пример 1. Умножить 2/5 на 0,8.
Пример 2. Умножить 0,28 на 6 1/4.
Ответ: 0,28 ∗ 6 1/4 = 0,8.
Запятая
Запятая — знак препинания в русском и многих других языках.
Содержание
Как знак препинания
В русском языке запятая используется на письме: Для обособления (выделения):
Как десятичный разделитель
В числовой записи запятой отделяется целая и дробная части
В информатике
В языках программирования запятая используется в основном при перечислении — например, аргументов функций, элементов массива.
Является разделителем в представление табличных данных в текстовом формате CSV.
Код запятой в Юникоде — 0x002C.
На современных компьютерных клавиатурах запятую можно набрать двумя способами:
В культуре
Точка, точка, запятая —
Вышла рожица кривая,
Палка, палка, огуречик,
Получился человечек.
См. также
Примечания
Ссылки
Полезное
Смотреть что такое «Запятая» в других словарях:
запятая — См. препятствие. Словарь русских синонимов и сходных по смыслу выражений. под. ред. Н. Абрамова, М.: Русские словари, 1999. запятая остановка, препятствие; запятушка, зацепка, затруднение, трудность, знак, закавычка, узкое место, закорючка,… … Словарь синонимов
ЗАПЯТАЯ — ЗАПЯТАЯ, запятой, жен. 1. Знак препинания (,), разделяющий синтаксические группы в пределах одного синтаксического целого (грам.). Поставить запятую. Поставить слова в запятых. Отделить запятою. 2. Препятствие, затруднение (разг. шутл.). Вот тут… … Толковый словарь Ушакова
ЗАПЯТАЯ — ЗАПЯТАЯ, запятие, запять и пр. см. запинать. Толковый словарь Даля. В.И. Даль. 1863 1866 … Толковый словарь Даля
запятая — (Comma) Одиночный разделительный знак препинания [точка, запятая, двоеточие, тире, многоточие и т.д.]. В русском языке употребляется при перечислениях, между однородными членами предложения и предложениями, при выделении причастных и… … Шрифтовая терминология
ЗАПЯТАЯ — знак препинания (,), употребляемый для выделения и отделения друг от друга различных составных частей простого и сложного предложений … Большой Энциклопедический словарь
ЗАПЯТАЯ — ЗАПЯТАЯ, ой, жен. 1. Знак препинания (,), обычно обозначающий интонационное членение, а также выделяющий нек рые синтаксические группы. 2. перен. Препятствие, затруднение (разг. шутл.). В этом то вся и з. • До последней запятой (знать, изучить)… … Толковый словарь Ожегова
запятая — точечный точка — [Л.Г.Суменко. Англо русский словарь по информационным технологиям. М.: ГП ЦНИИС, 2003.] Тематики информационные технологии в целом Синонимы точечныйточка EN point … Справочник технического переводчика
Запятая — см. Условные разделительные знаки (УРЗ) в библиогр. записи … Издательский словарь-справочник
ЗАПЯТАЯ — термин, относящийся к представлению действительного числа дробью, к способу представления действительных чисел в цифровой вычислительной машине. Пусть выбрана система счисления с основанием q, и пусть для действительного числа химеет место… … Математическая энциклопедия
Зачем нужны запятые?
Многие из нас «не дружат» с пунктуацией. Таким людям сложно запомнить правила расстановки запятых, поэтому эти знаки препинания они либо пропускают, либо переполняют ими текст. Конечно же, всем нам хотелось, чтобы запятых было меньше – ведь проще не задумываться над тем, где грамотно ее поставить.
Но это только одна точка зрения. А представьте, если бы запятых не было бы совсем. Получилась бы история, как в мультфильме «Страна Невыученных Уроков». Герой, попав в волшебную страну, должен был грамотно проставить в предложении знаки препинания, решив тем самым судьбу неизвестного бедняги.
Функции запятой
Конечно, через мультфильм дети проще понимают, зачем нужны запятые. Однако во взрослой жизни отсутствие запятых запутало бы всех: длинные предложения потеряли бы свой смысл, а короткие – стали односложными, обрубленными, потеряли бы интонацию и эмоциональный окрас.
Выражаясь умно, в тексте запятыми выделяют конструкции и простые предложения в составе сложных, разделяют перечисления, обособляют определения, обстоятельства, вводные слова и междометия, а также используют их для выделения прямой и косвенной речи.
Если говорить о запятой в контексте смыслового предназначения, то этот знак препинания придает предложению интонацию, при помощи которой значимые части текста можно «окрасить» различными эмоциональными оттенками.
При разделении смысловых блоков предложения запятая не только разделяет их, но связывает, наполняя определенным смыслом, как отдельные части, так и само предложение. Такая функция знака препинания отлично показана на примерах с пропущенной запятой, в которых значение фраз зависит от того, где стоит запятая. Правильно поставленный знак препинания придает тексту не только конкретный, но и понятный смысл.
Одна лишняя запятая в тексте, как говорил Иван Бунин, «…нарушает всю музыку», искажая понимание текста и усложняя его восприятие.
Если рассматривать все функции запятой, можно точно ответить на вопрос «Зачем нужны запятые?». Они, запятые, как ни один знак препинания, помогают донести значение любой письменной речи.
Как «работают» запятые?
Запятые в устной речи нужны для того, чтобы отражать особенности ее интонации. Если в конце любой устной фразы мы отчетливо делаем паузу, на письме ставим точку. При перечислении предметов или действий мы делаем небольшую паузу, в письменной речи однородные члены предложения разделяем запятыми. Итак, запятая в устной и письменной речи нужна для того, чтобы придать тексту необходимую интонацию и эмоциональный окрас.
В современной пунктуации функции запятой немного изменились – кроме интонации, запятая стала выражать синтаксическую структуру текста. Разделение текста запятыми, кроме обособления и перечисления, помогает структурировать его, разбив более сложные предложения на простые. Это позволяет не только легко зрительно воспринимать текст, но и правильно понимать его, как того хотел автор. Итак, вторая функция запятой – помощь в восприятии текста.
Как красота может изменить мир, так и запятая может в корне поменять смысл предложения (вспомните примеры с пропущенной запятой). Именно эта функция запятой является самой безусловной.
Запятые в пунктуации
Запятая является письменным знаком препинания, который используется во многих языках.
Зачем нужны запятые в русском языке? В пунктуации русского языка запятые используют для выделения частей речи: некоторых определений и обстоятельств, обращений, уточнений, вводных слов или предложений, междометий. Запятые разделяют сложносочиненные, сложноподчиненные и сложные бессоюзные предложения, однородные члены предложения при перечислении; разделяют прямую и косвенную речь.
Запятые в математике
Запятые в информатике
Запятые широко используются в языках программирования при перечислении элементов массивов, аргументов функций и других подобных элементов.
Запятыми разделяют табличные данные в текстовом формате CSV.
Запятые в культуре
В детских считалочках часто можно встретить строчки про запятую – «Точка, точка, запятая…». Кроме этого, запятая часто становилась героиней детских мультфильмов – «Приключения запятой и точки» и «В Стране Невыученных Уроков».
Плавающая запятая
Плавающая запятая — форма представления дробных чисел, в которой число хранится в форме мантиссы и показателя степени. При этом число с плавающей запятой имеет фиксированную относительную точность и изменяющуюся абсолютную. Наиболее часто используемое представление утверждено в стандарте IEEE 754. Реализация математических операций с числами с плавающей запятой в вычислительных системах может быть как аппаратная, так и программная.
Содержание
«Плавающая запятая» и «плавающая точка»
Так как в некоторых, преимущественно англоязычных и англофицированных, странах (см. подробный список Decimal separator (англ.) ) при записи чисел целая часть отделяется от дробной точкой, то в терминологии этих стран фигурирует название «плавающая точка» (floating point (англ.) ). Так как в России целая часть числа от дробной традиционно отделяется запятой, то для обозначения того же понятия используется термин «плавающая запятая».
Происхождение названия
Название «плавающая запятая» происходит от того, что запятая в позиционном представлении числа (десятичная запятая, или, для компьютеров, двоичная запятая — далее по тексту просто запятая) может быть помещена где угодно относительно цифр в строке. Это положение запятой указывается отдельно во внутреннем представлении. Таким образом, представление числа в форме с плавающей запятой может рассматриваться как компьютерная реализация экспоненциальной записи чисел.
Преимущество использования представления чисел в формате с плавающей запятой над представлением в формате с фиксированной запятой (и целыми числами) состоит в том, что можно использовать существенно больший диапазон значений при неизменной относительной точности. Например, в форме с фиксированной запятой число, занимающее 8 разрядов в целой части и 2 разряда после запятой, может быть представлено в виде 123456,78; 8765,43; 123,00 и так далее. В свою очередь, в формате с плавающей запятой (в тех же 8 разрядах) можно записать числа 1,2345678; 1234567,8; 0,000012345678; 12345678000000000 и так далее.
Скорость выполнения компьютером операций с числами, представленными в форме с плавающей запятой, измеряется в англ. FLOPS — число операций с плавающей запятой в секунду ),
Структура числа
Число с плавающей запятой состоит из:
Нормальная форма
Использование в вычислительных машинах
Краткий обзор
Существует несколько способов того, как строки из цифр могут представлять числа:
Запись числа в форме с плавающей запятой позволяет производить вычисления над широким диапазоном величин, сочетая фиксированное количество разрядов и точность. Например, в десятичной системе предоставления чисел с плавающей запятой (3 разряда) операцию умножения, которую мы бы записали как
в нормальной форме представляется в виде
(1,20 × 10 −1 ) × (1,20 × 10 −1 ) = (1,44 × 10 −2 ).
В формате с фиксированной запятой мы бы получили вынужденное округление
Мы потеряли крайний правый разряд числа, так как данный формат не позволяет запятой «плавать» по записи числа.
Диапазон чисел, представимых в формате с плавающей запятой
Диапазон чисел, которые можно записать данным способом, зависит от количества бит, отведённых для представления мантиссы и показателя. На обычной 32-битной вычислительной машине, использующей двойную точность (64 бита), мантисса составляет 52 бита + 1 знаковый, показатель — 11 бит. Таким образом получаем диапазон точности примерно от 4,94 × 10 −324 до 1.79 × 10 308 (от 2 −52 × 2 −1022 до
1 × 2 1024 ). Пара значений показателя зарезервирована для обеспечения возможности представления специальных чисел. К ним относятся значения бесконечность), получающихся в результате операций типа деления на ноль нуля, положительных и отрицательных чисел. Также сюда попадают денормализованные числа, у которых мантисса меньше единицы. В специализированных устройствах (например GPU) поддержка специальных чисел часто отсутствует. Существуют программные пакеты, в которых объём памяти выделенный под мантиссу и показатель задаётся программно, и ограничивается лишь объёмом доступной памяти ЭВМ.
Машинный эпсилон
В отличие от фиксированной запятой, сетка чисел, которые способна отобразить арифметика с плавающей запятой, неравномерна: она более густая для чисел малого порядка и более редкая — для больших чисел. Но относительная погрешность записи чисел одинакова и для малых чисел, и для больших. Поэтому можно ввести понятие машинного эпсилона.
Машинным эпсилоном называется наименьшее положительное число ε такое, что 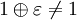

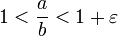


.svg.png)
