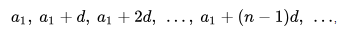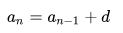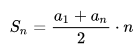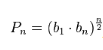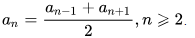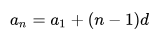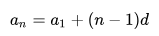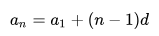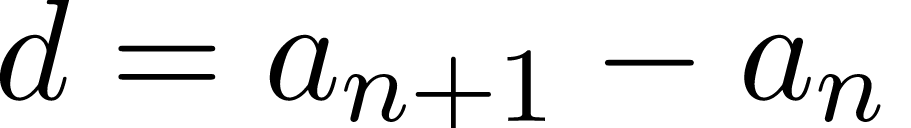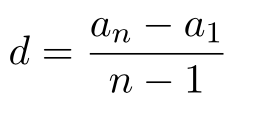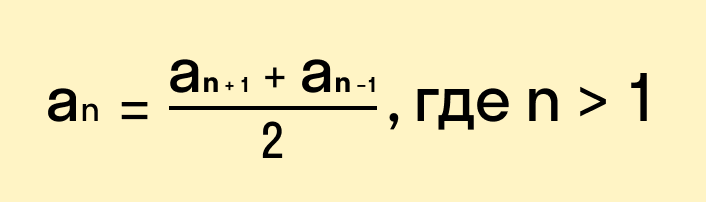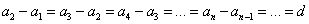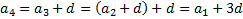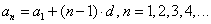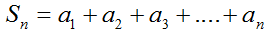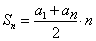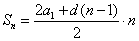Как называется сумма последовательных чисел
Арифметическая прогрессия и сумма ее членов
теория по математике 📈 последовательности
Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, равен предыдущему, сложенному с одним и тем же числом.
Другими словами, последовательность (аn) – арифметическая прогрессия, если для любого натурального числа n выполняется условие аn+1=аn+d, где d – некоторое число. Из данного равенства следует, что можно найти это число d, если вычесть из последующего члена предыдущий, то есть d = аn+1–аn. Число d называют разностью арифметической прогрессии.
Арифметической прогрессией, например, является ряд чисел 3; 8; 13; 18…. так как разница между числами равна 5, мы видим, что каждое последующее на 5 больше предыдущего.
Если известен первый член арифметической прогрессии a1 и разность d, то можно вычислить любой член арифметической прогрессии:
Этот ряд можно продолжать до бесконечности, поэтому надо запомнить, что n-ый член арифметической прогрессии можем получить быстрее, если к первому члену прогрессии добавить (n−1) разностей, то есть:
Формула n-ого члена арифметической прогрессии
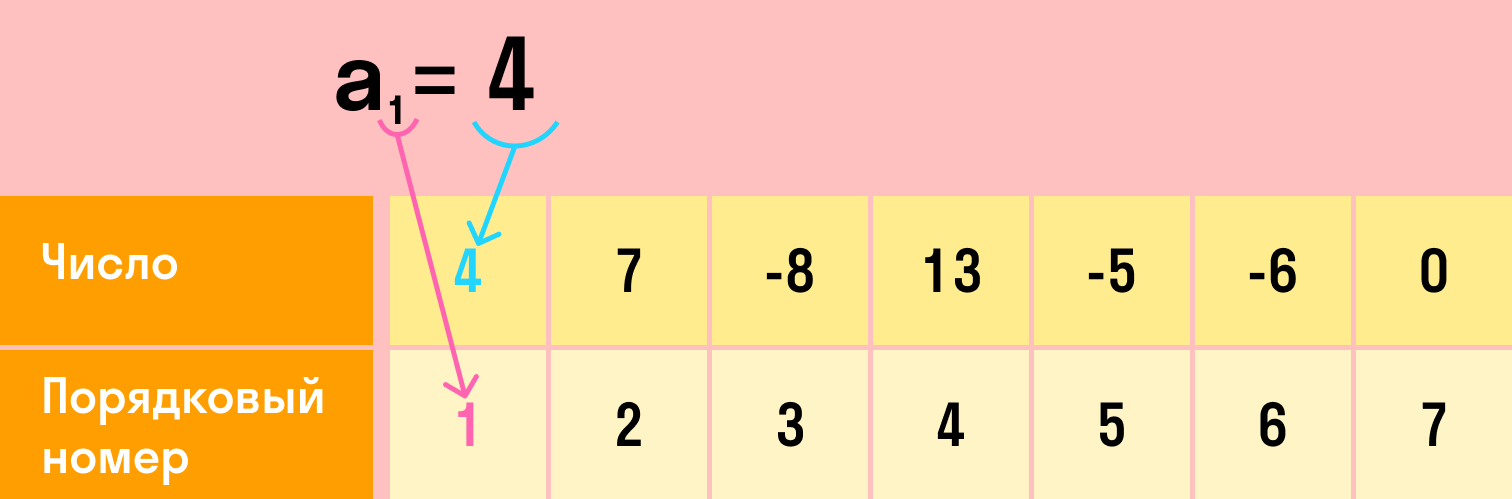
где n – порядковый номер члена арифметической прогрессии, a1 – первый член прогрессии, d – разность арифметической прогрессии
Формулу используют, чтобы вычислить заданный член арифметической прогрессии (например, пятнадцатый, двухсотый и т.д.), если известны первый член последовательности и ее разность. Рассмотрим на примерах применение данной формулы.
Пример №1. Найти а20 арифметической прогрессии (аn), если а1=14, d=5. Составляем формулу для а20 и подставляем в нее данные: а20= a1 + d(20−1)=14+5(20−1)=109. Таким образом, мы вычислили, что на 20-ом месте в данной арифметической прогрессии стоит число 109.
Найти а7 арифметической прогрессии (аn), если а1=−8, d=−3. Аналогично работаем, составляя формулу и подставляя в нее данные значения (обращаем внимание на знаки чисел, чтобы не допустить ошибок): а7= a1 + d(7−1)= −8−3(7−1)= −26.
Дана арифметическая прогрессия 10; 12; 14;…… Найти а12. Здесь для нахождения а12 надо сначала найти разность d: d=12−10=2, то есть из последующего вычтем предыдущее. Можно было 14−12, порядок здесь не имеет значения, главное берем два соседних члена прогрессии. Теперь можем составлять формулу и находить а12: а12= a1 + d(12−1)=10+2(12−1)=32.
Любая арифметическая прогрессия может быть задана формулой вида an=kn+b, где k и b некоторые числа. Верно и обратное утверждение: если последовательность чисел задана формулой вида an=kn+b, где k и b некоторые числа, то она является арифметической.
Так, например, формула an=5n+1 задает арифметическую прогрессию, в которой разность d равна 1; по данной формуле можно найти любой член последовательности, например, найдем 20-ый член, подставляя в формулу число 20: a20=5 × 20+1=101.
Свойство арифметической прогрессии
Каждый член арифметической прогрессии, начиная со второго, равен среднему арифметическому предыдущего и последующего членов. Формула:
Другими словами, используя данное свойство, мы можем найти член арифметической прогрессии, стоящий между двумя известными членами, без использования разности d. Рассмотрим это на примерах.
Пример №2. Найти а10 арифметической прогрессии (аn), если а9=24; а11=38. Здесь используем свойство, так как видим, что у а10 известны соседние члены. Значит, а10=(а9+а11):2=(24+38):2=31. Таким образом, десятый член равен 31.
Дана арифметическая прогрессия …..23; х; 35. Найти х. Применяем свойство для нахождения х: х=(23+35):2=29. Для наглядности запишем, что ряд чисел выглядит так: …23; 29; 35.
Формулы суммы n первых членов арифметической прогрессии
В данной формуле мы видим, что для нахождения суммы нужны первый и последний член прогрессии. Но встречаются случаи, когда аn не известно, но известна разность. Тогда для нахождения суммы применяют вторую формулу.
Формула суммы членов арифметической прогрессии с первым членом и разностью
Рассмотрим на примерах применение данных формул.
Пример №3. Найти сумму первых пятидесяти членов арифметической прогрессии (аn), если а1=11, а50=39.
Для решения лучше использовать первую формулу, так как здесь есть первый и последний члены: а1=11, а50=39. Поэтому составляем формулу, подставляем в нее данные значения и вычисляем:
Найти сумму первых десяти членов арифметической последовательности 3; 18; …. В данном случае задание можно выполнить двумя способами, как по первой формуле, так и по второй, а затем выяснить, какой способ короче, а значит, рациональнее.
Способ №1 (по первой формуле): надо найти разность d, затем десятый член прогрессии, а затем сумму:
Способ №2 (по второй формуле): надо знать разность d, d=18-3=15. Теперь подставим значения во вторую формулу и сосчитаем результат:
Результаты в обоих случаях получились у нас одинаковые. А если сравнить два способа, то видно, что второй способ быстрее, тем более что в большинстве случаев разность арифметической прогрессии можно вычислить устно.
Таким образом, выбор формулы для нахождения суммы n первых членов арифметической прогрессии зависит от заданного условия.
-6-8=-14 через 1 минуту
-14-8=-22 через 2 минуты
-22-8=-30 через 3 минуты
-30-8=-38 через 4 минуты
-38-8=-46 через 5 минут
-46-8=-54 через 6 минут
Вторым способом является решение по формуле n-ого члена арифметической прогрессии, которая есть также и в справочном материале, т.е. an=a1+d(n – 1). В данном случае a1=-6; d=-8, n=7 (так как ЧЕРЕЗ 6 минут). Подставим значения в формулу: a7=-61-8(7 – 1). Вычислим: a6=-6-8 ∙ 5=-6-48=-54.
pазбирался: Даниил Романович | обсудить разбор | оценить
Содержание данной задачи говорит нам о том, что здесь есть арифметическая прогрессия, так как число жителей города возрастало на одну и ту же величину.
2008 г – 38100 человек
2016 г. – 43620 человек
Итак, можно вычислить прирост населения с 2008 по 2016 ежегодно:
(43620 – 38100):(2016 – 2008)= 5520:8=690 человек.
Теперь можно найти, сколько человек проживало в конце 2012 года.
38100+690(2016 – 2012)= 40860 человек
pазбирался: Даниил Романович | обсудить разбор | оценить
pазбирался: Даниил Романович | обсудить разбор | оценить
В содержании задачи есть фраза, что акции дорожали ежедневно на одну и ту же сумму, следовательно, имеем арифметическую прогрессию. Итак, определяем, что известно: в 7-й день акция стоила 777 рублей, это а7=777; в 12-й день – 852 рубля, это а12=852. Известно, что акции дорожали 25 дней, а найти надо стоимость акции в последний, т.е. в 25-ый день, значит, будем искать а25.
1 способ:
В данной арифметической прогрессии нет первого члена, не идет речь про сумму, поэтому воспользуемся формулой аn=ak+d(n – k), где n>k. Числа n и k – это порядковые номера. Составим формулу для наших данных и подставим в неё значения: а12=а7+d(12-7); 852=777+d(12 – 7). Упростим выражение и найдем разность d, 852–777= d(12 – 7); 75= d∙5; отсюда d=75:5=15. Итак, мы нашли, что акции ежедневно дорожали на 15 рублей.
Теперь, зная число d, мы можем найти а25 через, например, а12, используя всё ту же формулу. Получаем: а25=а12+d(25-12); а25=852+15(25-12)=852+15∙13= 852+195=1047. Значит, 1047 рублей стоила акция в последний день.
2 способ:
pазбирался: Даниил Романович | обсудить разбор | оценить
В условии задачи встречаются слова, что норма увеличивалась на одно и то же число. И это значит, что мы имеем арифметическую прогрессию, в которой а1=6, так как в первый день перевезли 6 тонн. Далее, известно, что вся работа была выполнена за 11 дней, значит число n=11. Так как масса всего щебня равна 176, то это число является суммой нашей прогрессии, т.е. S11=176. Требуется найти, сколько тонн было перевезено в последний день, а он – 11, значит, найти надо а11.
pазбирался: Даниил Романович | обсудить разбор | оценить
Из содержания данной задачи видно, что время процедуры увеличивалось с каждым днем на одно и то же количество времени – на 15 минут, следовательно, это арифметическая прогрессия. Так как в первый день курс был 15 минут, то а1=15; так как время ежедневно увеличивалось на 15 минут, то значит разность d=15; зная, что продолжительность процедуры должна достигнуть 1 ч 15 мин, т.е. достигнуть 75 минут (1 час=60 мин, плюс 15 минут), то это число 75 и будет являться n членом арифметической прогрессии. Требуется найти, в какой по счету день продолжительность процедуры достигнет этих 75 минут, т.е. найдем число n.
Теперь берем формулу n члена арифметической прогрессии аn=a1+d(n – 1) и подставляем в неё наши данные: 75=15+15(n – 1); упростим данное выражение: 75-15=15(n – 1); 60=15(n – 1); разделим на 15 обе части: 4=n – 1; найдем отсюда, что n=5. Таким образом, на пятый день продолжительность процедуры достигнет 75 минут.
pазбирался: Даниил Романович | обсудить разбор | оценить
Анализируя содержание задачи, мы видим, что улитка проползала ежедневно на одно и то же расстояние меньше, чем в предыдущий день. А это значит, что имеем арифметическую прогрессию. По условию определяем данные: так как в первый и последний дни она проползла 7,5 м, то имеем, что а1+аn=7,5. Так как расстояние между деревьями равно 60 м, то имеем сумму n первых членов прогрессии, т.е. Sn=60. Так как найти надо количество дней, которое она потратила на весь путь, то искомым числом будет число n.
Зная формулу суммы n первых членов арифметической прогрессии
pазбирался: Даниил Романович | обсудить разбор | оценить
При анализе содержания задачи мы видим, что каждую минуту количество осадка увеличивается на одно и то же число, на 0,2 г. А это значит, что имеем арифметическую прогрессию, в которой первый член равен 0,2, так как по условию в первую минуту образовалось 0,2 г осадка. Разность арифметической прогрессии равна также 0,2, так как каждую минуту на это количество увеличивается количество осадков. Найти нужно седьмой член последовательности.
Итак, имеем а1=0,2; d=0,2. Ищем а7. По определению n-ого члена арифметической прогрессии имеем формулу аn=a1+d(n – 1). Подставим в нее наши данные: а7=a1+d(7 – 1)=0,2+0,2·6=1,4
pазбирался: Даниил Романович | обсудить разбор | оценить
Арифметическая (алгебраическая) прогрессия определение, примеры нахождения с решением
Часто, при решении задач, связанных с наблюдениями и присвоением значения определенному событию за определенный промежуток времени, получается ряд чисел, который именуется арифметической прогрессией.
Одна из главных отличительных особенностей такая математическая модель имеет закономерность, по которой можно вычислить любой неизвестный член, что упрощает прогнозирование при вычислении физических ситуаций.
Примерами повседневного использования могут являться наблюдение за температурой воздуха, прогнозирование расходов с занесением результатов в таблицу и др.
Онлайн-калькулятор арифметической прогрессии
Определение и примеры арифметической прогрессии
Это последовательность из чисел, где каждое последующее число ряда (начиная со второго) увеличивается или уменьшается на определенную сумму, являющуюся константой.
Кроме этого для описания используется ряд сопутствующих терминов и определений. Членом (аn) называется единичное число из последовательности.
Разностью (d) называется фиксированное число, на которое увеличивается или уменьшается последующее число прогрессии.
Кроме этого, существуют виды таких рядов:
В качестве примера представим последовательность чисел «3, 9, 15, 21, 27». Данный случай – этот ряд чисел попадает под характеристику арифметической прогрессии. Этот вывод делается в том случае, когда разница между членами ряда фиксирована и равняется 6.
Виды арифметической (алгебраической) прогрессии
Разновидности строятся на основании характеристики разности (d), а именно на основании отличия последней от нуля.
Таким образом, можно встретить определенные вариации:
Если прогрессия не изменяется с каждым шагом на одну и ту же разность, то эта прогрессия непостоянная и арифметической не является.
Важно знать: арифметическая от геометрической отличается тем, что в последней производится увеличение каждого последующего на один и тот же множитель.
Формулы арифметической прогрессии
Одно из важнейших свойств заключается в возможности вычисления любого числа конкретного места ряда.
Чтобы решать это, необходима формула, показывающая, как находится член арифметической прогрессии. В общем виде она будет выглядеть, как значение предыдущего числа в ряду (an-1), к которому прибавляют разность (d):
Также может возникнуть задача, когда надо просуммировать все числа ряда арифметической прогрессии (сумма членов). Если их малое количество, то можно посчитать это вручную, но если количество чисел перевалит за сотню, то проще будет воспользоваться специальной формулой для обработки.
Итак, нам понадобится значение первого числа в ряду (a1) и последнего (an), а также информация об общем количестве чисел в ряду. Рекуррентная формула, показывающая, как искать сумму, будет выглядеть в таком случае следующим образом:
Обратите внимание: под значением n подразумевается именно количество членов ряда, для которых производится нахождение суммы.
Произведение членов арифметической прогрессии можно находить по похожей формуле:
где, Pn – произведение, b1 и bn – соответственно первое и последнее числа, а n – количество членов.
Отдельно следует коснуться такого понятия, как характеристическое свойство прогрессии. Оно сводится к выполнению определенного условия для каждого элемента:
Примеры задач с решением
Рассмотрим как решать задачи на заданную тему.
Пример 1
Требуется вычислить 574 член в ряду арифметической прогрессии, первые три члена которой «8, 15, 22…».
Вариант рассуждений по примеру 1. Для нахождения любого конкретного элемента ряда нам необходима информация о значении первого члена (a1) и о разности (d). Чтобы вычислить разность, вычитаем из второго члена ряда первый (15 – 
Подставляя полученные значения, получим выражение вида a574 = 8 + (574-1) * 7.
После вычисления получаем ответ: a574 = 4019.
Пример 2
Требуется вычислить 544 член ряда, являющийся арифметической прогрессией, при условии, что 154-ый член равен 17, а разность (d) равна 8.
Вариант рассуждений по примеру 2. Пользоваться в данной ситуации мы будем формулой из предыдущего примера:
Подставляя известные значения, получаем выражение – а544 = 17 + (544 1) * 8.
Вычисляя, получаем ответ а544 = 4361.
Пример 3
Для подготовки к экзамену по биологии студенту Смирнову необходимо выучить 730 вопросов (включая загадки). Известно, что он весьма обеспокоен и по мере приближения даты экзамена учит ежедневно на 27 вопросов больше, чем в предыдущий день. Друг Смирнова выяснил, что тот в первый день выучил всего 17 вопросов.
Требуется выяснить, сколько времени у студента ушло на подготовку.
Вариант рассуждений по примеру 3. Очевидно, что случай с подготовкой студента к экзамену решается через формулы арифметической прогрессией (поскольку присутствует фиксированная разность d = 17). Производим подстановку известных данных:
После подстановки получаем выражение: 730 = 17 + (n 1) * 27.
После вычислений определяем ответ – 27 дней.
Арифметическая прогрессия является наиболее простой из всех числовых зависимостей. Использование описанных формул позволит намного ускорить вычисления в задачах, где это требуется.
Кроме этого, для упрощения можно использовать онлайн калькулятор. В школе данную тему изучают в программе за 9 класс, а основные задания касаются нахождения членов и сумм.
Арифметическая прогрессия: свойства и формулы
Определение числовой последовательности
Числовая последовательность — это множество чисел, каждому из которых можно присвоить уникальный номер.
Последовательности можно задавать разными способами:
«Последовательность простых чисел: 2, 3, 5, 7, 11, 13, 17, 19, 23. »
Последовательность yn = C называют постоянной или стационарной.
Последовательность Фибоначчи — когда каждое следующее число равно сумме двух предыдущих чисел: an+1 = an + an-1.
Пример: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55.
Так как алгебраическая числовая последовательность — это частный случай числовой функции, то ряд свойств функций рассматриваются и для последовательностей.
Свойства числовых последовательностей:
Возрастающие и убывающие последовательности называют монотонными последовательностями.
Запишем числа, которые первые пришли в голову: 7, 19, 0, −1, −2, −11, 0… Сколько бы чисел не написали, всегда можно сказать, какое из них первое, какое — второе и так до последнего. То есть мы можем их пронумеровать.
Пример числовой последовательности выглядит так:
В такой математической последовательности каждый номер соответствует одному числу. Это значит, что в последовательности не может быть двух первых чисел и т.д. Первое число (как и любое другое) — всегда одно.
N-ный член алгебраической последовательности — это число с порядковым номером n.
Всю последовательность можно обозначить любой буквой латинского алфавита, например, a. Каждый член этой последовательности — той же буквой с индексом, который равен номеру этого члена: a1, a2. a10. an.
N-ый член последовательности можно задать формулой. Например:
Определение арифметической прогрессии
Так как числовая последовательность — это частный случай функции, которая определена на множестве натуральных чисел, арифметическую прогрессию можно назвать частным случаем числовой последовательности.
Рассмотрим основные определения и как найти арифметическую прогрессию.