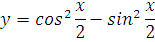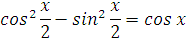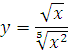Как называется штрих в математике
Что такое производная?
Таблица производных.
Это знакомство позволит:
— понимать суть несложных заданий с производной;
— успешно решать эти самые несложные задания;
— подготовиться к более серьёзным урокам по производной.
Строгое определение производной основано на теории пределов и штука достаточно сложная. Это огорчает. Но практическое применение производной, как правило, не требует таких обширных и глубоких знаний!
Приступим к знакомству?)
Термины и обозначения.
В элементарной математике много всяких математических операций. Сложение, вычитание умножение, возведение в степень, логарифмирование и т.д. Если к этим операциям добавить ещё одну, элементарная математика становится высшей. Эта новая операция называется дифференцирование. Определение и смысл этой операции будут рассмотрены в отдельных уроках.
Зная термины, можно, как минимум, понимать задания.) Формулировки бывают такие: найти производную функции; взять производную; продифференцировать функцию; вычислить производную и т.п. Это всё одно и то же. Разумеется, бывают и более сложные задания, где нахождение производной (дифференцирование) будет всего лишь одним из шагов решения задания.
Обозначается производная с помощью штришка вверху справа над функцией. Вот так: y’ или f'(x) или S'(t) и так далее.
Читается игрек штрих, эф штрих от икс, эс штрих от тэ, ну вы поняли. )
Штрих также может обозначать производную конкретной функции, например: (2х+3)’, (x 3 )’, (sinx)’ и т.д. Часто производная обозначается с помощью дифференциалов, но такое обозначение в этом уроке мы рассматривать не будем.
Чтобы найти производную функции, надо знать всего три вещи. Три кита, на которых стоит всё дифференцирование. Вот они эти три кита:
1. Таблица производных (формулы дифференцирования).
3. Производная сложной функции.
Начнём по порядку. В этом уроке рассмотрим таблицу производных.
Таблица производных.
Рассмотрим несколько примеров:
1. Найти производную функции y = x 3
Такой функции в таблице нет. Но есть производная степенной функции в общем виде (третья группа). В нашем случае n=3. Вот и подставляем тройку вместо n и аккуратно записываем результат:
(x 3 )‘ = 3·x 3-1 = 3x 2
Ответ: y’ = 3x 2
2. Найти значение производной функции y = sinx в точке х = 0.
По табличке находим синус и соответствующую производную:
Подставляем ноль в производную:
3. Продифференцировать функцию:
Что, внушает? ) Такой функции в таблице производных и близко нет.
Да-да! Запомните, что преобразование исходной функции до дифференцирования вполне допускается! И, случается, здорово облегчает жизнь. По формуле косинуса двойного угла:
Пример для продвинутых выпускников и студентов:
4. Найти производную функции:
Такой функции в таблице производных нет, разумеется. Но если вспомнить элементарную математику, действия со степенями. То вполне можно упростить эту функцию. Вот так:
Вот и всё. Это будет ответ.
Таблица производных функций
10 класс, 11 класс, ЕГЭ/ОГЭ
Статья находится на проверке у методистов Skysmart.
Если вы заметили ошибку, сообщите об этом в онлайн-чат
(в правом нижнем углу экрана).
Что такое производная и зачем она нужна
Прежде чем переходить к таблице для вычисления производных, дадим определение производной. В учебнике оно звучит так:
Производная функции — это предел отношения приращения функции к приращению ее аргумента, при условии, что приращение аргумента стремится к нулю.
Если же говорить простыми словами, то производная функции описывает, как и с какой скоростью эта функция меняется в данной конкретной точке. Процесс нахождения производной называется дифференцированием.
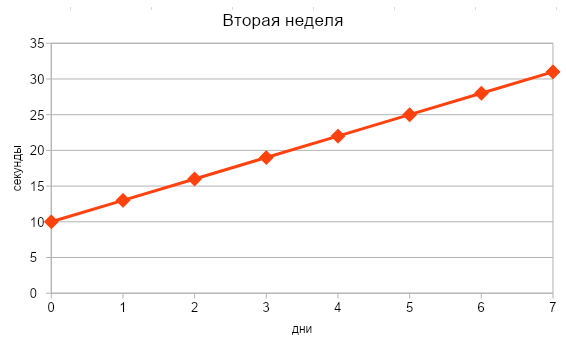
Объясним на примере: допустим, Маша решила по утрам делать зарядку и стоять в планке. В первую неделю она держалась каждый день по 10 секунд, но начиная со второй недели смогла стоять в планке с каждым днем на 3 секунды дольше. Успехи Маши можно описать следующими графиками:
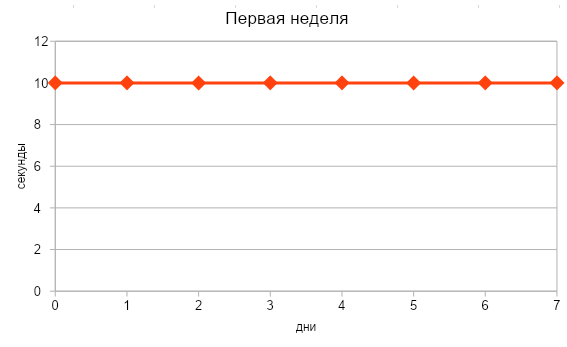
Очевидно, что в первую неделю результаты Маши не менялись (т. е. были константой), скорость прироста оставалась нулевой. Если мы заглянем в таблицу производных простых функций, то увидим, что производная константы равна нулю.
Во вторую неделю время выполнения планки с 10 сек начало увеличиваться на 3 сек ежедневно.
Снова смотрим в таблицу дифференцирования производных, где указано, что производная от х равна 1.
Вот так с помощью таблицы производных и элементарной математики мы докажем, что успехи Маши росли со скоростью 3 сек в день.
Это был очень простой пример, который в общих чертах объясняет азы дифференциального исчисления и помогает понять, для чего нужны формулы из таблицы производных функций. Но разобраться в решении задач, где скорость меняется нелинейно, конечно, не так просто.
Быстрее освоить производные поможет обучение на курсах по математике в онлайн-школе Skysmart.
Производные основных элементарных функций
Таблица производных для 10 и 11 класса может включать только элементарные часто встречающиеся функции. Поэтому приведем стандартную таблицу производных.
Решение производной для чайников: определение, как найти, примеры решений
Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.
Геометрический и физический смысл производной
Пусть есть функция f(x), заданная в некотором интервале (a, b). Точки х и х0 принадлежат этому интервалу. При изменении х меняется и сама функция. Изменение аргумента – разность его значений х-х0. Эта разность записывается как дельта икс и называется приращением аргумента. Изменением или приращением функции называется разность значений функции в двух точках. Определение производной:
Производная функции в точке – предел отношения приращения функции в данной точке к приращению аргумента, когда последнее стремится к нулю.
Иначе это можно записать так:
Какой смысл в нахождении такого предела? А вот какой:
Геометрический смысл производной: производная от функции в точке равна тангенсу угла между осью OX и касательной к графику функции в данной точке.
Физический смысл производной: производная пути по времени равна скорости прямолинейного движения.
Действительно, еще со школьных времен всем известно, что скорость – это частное пути x=f(t) и времени t. Средняя скорость за некоторый промежуток времени:
Чтобы узнать скорость движения в момент времени t0 нужно вычислить предел:
Кстати, о том, что такое пределы и как их решать, читайте в нашей отдельной статье.
Приведем пример, иллюстрирующий практическое применение производной. Пусть тело движется то закону:
Нам нужно найти скорость в момент времени t=2c. Вычислим производную:
Правила нахождения производных
Сам процесс нахождения производной называется дифференцированием. Функция, которая имеет производную в данной точке, называется дифференцируемой.
Как найти производную? Согласно определению, нужно составить отношение приращения функции и аргумента, а затем вычислить предел при стремящемся к нулю приращении аргумента. Конечно, можно вычислять все производные так, но на практике это слишком долгий путь. Все уже давно посчитано до нас. Ниже приведем таблицу с производными элементарных функций, а затем рассмотрим правила вычисления производных, в том числе и производных сложных функций с подробными примерами.
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы
Правило первое: выносим константу
Пример. Вычислим производную:
Правило второе: производная суммы функций
Производная суммы двух функций равна сумме производных этих функций. То же самое справедливо и для производной разности функций.
Не будем приводить доказательство этой теоремы, а лучше рассмотрим практический пример.
Найти производную функции:
Правило третье: производная произведения функций
Производная произведения двух дифференцируемых функций вычисляется по формуле:
Пример: найти производную функции:
Здесь важно сказать о вычислении производных сложных функций. Производная сложной функции равна произведению производной этой функции по промежуточному аргументу на производную промежуточного аргумента по независимой переменной.
В вышеуказанном примере мы встречаем выражение:
В данном случае промежуточный аргумент – 8х в пятой степени. Для того, чтобы вычислить производную такого выражения сначала считаем производную внешней функции по промежуточному аргументу, а потом умножаем на производную непосредственно самого промежуточного аргумента по независимой переменной.
Правило четвертое: производная частного двух функций
Формула для определения производной от частного двух функций:
Мы постарались рассказать о производных для чайников с нуля. Эта тема не так проста, как кажется, поэтому предупреждаем: в примерах часто встречаются ловушки, так что будьте внимательны при вычислении производных.
С любым вопросом по этой и другим темам вы можете обратиться в студенческий сервис. За короткий срок мы поможем решить самую сложную контрольную и разобраться с заданиями, даже если вы никогда раньше не занимались вычислением производных.
Иван Колобков, известный также как Джони. Маркетолог, аналитик и копирайтер компании Zaochnik. Подающий надежды молодой писатель. Питает любовь к физике, раритетным вещам и творчеству Ч. Буковски.
Штрихи, штришки и штришочки
На стандартной PC-клавиатуре есть три символа со штрихами: «’» и «»» на кнопке вместе с русской «э», а также «`» на периферийной кнопке с буквой «ё».
Ни один из этих символов не используется при нормальном, грамотном наборе текста. Однако, нельзя отрицать важность символов «’» и «»» при программировании и вёрстке HTML, чего мы делать и не будем.
| ‘ | U+0027 | апостро́ф | Этот знак действительно называется «APOSTROPHE» в Unicode, находится там, потому что так исторически сложилось в кодировке ASCII. Стандарт Unicode специально подчёркивает, что символ U+0027 имеет широкое использование, а собственно в роли апострофа должен выступать другой знак, о котором речь пойдёт ниже. |
| « | U+0022 | кавычка | Просто «кавычка», «QUOTATION MARK». Имеет широкое использование, но в качестве собственно текстовых кавычек рекомендованы другие символы, о которых речь также пойдёт ниже. |
| ` | U+0060 | гра́вис | Гравис используется для того, чтобы акцентировать гласные в некоторых европейских языках: французском (déjà vu), итальянском (virtù), португальском, валлийском (mẁg) и других. Таким образом, гравис совершенно не употребляется в современном русском языке, а также не имеет никакого отношения к апострофам или кавычкам. |
Ошибки трактования этих знаков встречаются достаточно часто. В «Живой типографике» символ «»» спутан со знаком секунды (о котором я также расскажу ниже), в некоторых пособиях гравис называют обратным апострофом, и так далее.
Я предлагаю называть по-русски «’» стандартным или машинописным апострофом, «»» — стандартной или машинописной кавычкой, а «`», как ему и положено, грависом.
Правильные кавычки
О кавычках я писал в статье Оформление цитат на сайтах, но будет нелишним напомнить ещё раз, поразвёрнутее.
| « | U+00AB | открывающая кавычка-ёлочка | Вот они, настоящие, правильные, традиционные кавычки-ёлочки. Именно так должны выглядеть основные кавычки в русскоязычном текстовом наборе. Они не должны отбиваться пробелами от текста, который они окружают. |
| » | U+00BB | закрывающая кавычка-ёлочка | |
| „ | U+201E | открывающая кавычка-лапка | А это — настоящие традиционные кавычки второго рисунка, „лапки“. Именно так должны выглядеть вложенные кавычки в русскоязычном текстовом наборе. Они также не отбиваются пробелами от окружённого ими текста. Так уж сложилось, что кавычки-лапки заимствованы из немецкой типографики, а Unicode базировался на типографике американской. Поэтому наша открывающая кавычка называется в Unicode просто «двойной нижней из девяток» (потому что запятые обращены вниз и похожи на две цифры 9), а наша закрывающая кавычка наоборот называется «двойной открывающей». |
| “ | U+201C | закрывающая кавычка-лапка | |
| ‘ | U+2018 | открывающая ма́рровская кавычка | «Марровская» — это, пожалуй, жаргонизм. Правильно эти кавычки называются английскими одинарными. Эти кавычки используются только в филологии, где их ввёл в первой половине XX века академик Н. Я. Марр. Они используются для того, чтобы обозначить некоторое слово, значение слова или его происхождение («от латинского appellatio ‘сообщение’», «со словом ‘посёлок’ не склоняется»). Найти марровские кавычки можно в любом содержательном словаре, но обычному человеку (не филологу) эти кавычки употреблять не нужно, потому что незачем. В некотором смысле, это узкоспециальные знаки. |
| ’ | U+2019 | закрывающая ма́рровская кавычка |
Я предлагаю называть кавычки либо по рисунку (кавычки-ёлочки, кавычки-лапки, марровские кавычки), либо собирательно «традиционные кавычки», чтобы отличать их от стандартной (машинописной) кавычки, которая есть у нас на клавиатуре.
Стоит упомянуть, что в шрифте Verdana в MS Windows (в том числе и в версии 5.01) закрывающая кавычка-лапка (она же открывающая двойная английская кавычка) имеет неправильный рисунок (штрихи развёрнуты вниз, а не вверх), так что не пугайтесь.
Апостроф
| ’ | U+2019 | апостро́ф | Кажется, мы это только что видели? Бинго! Для апострофа Unicode рекомендует к использованию тот же самый символ, который является английской одинарной закрывающей кавычкой (он же — закрывающая марровская кавычка). |
В русском языке апостроф используется достаточно редко. В основном — в иностранных именах, где в родном языке стоит апостроф: Д’Артаньян, Сара О’Коннор, и так далее. Сейчас учащается использование апострофа при наращении иностранных слов и наименований, не транскрибированных на русский: «Intel’овский процессор», «скинуть e-mail’ом». Раньше такое употребление считалось неверным, но норма языка изменилась на наших глазах, и теперь такое употребление допустимо.
Я предлагаю называть этот апостроф традиционным апострофом, в отличие от стандартного (машинописного) апострофа. Традиционный апостроф включён в ряд «типографских» раскладок клавиатуры и доступен для набора с клавишей AltGr.
Наверное, стоит упомянуть, что в Unicode есть ещё апостроф-буква (U+02BC), который имеет семантику именно буквы, а не орфографического знака. Апостроф используется в качестве буквы в некоторых языках, но к русскому это отношения не имеет.
Знак ударения
| ´ | U+0301 | знак ударения, аку́т | Знак ударения используется, чтобы отличать слова «стои́т» и «сто́ит», «больша́я» и «бо́льшая», «уже́» и «у́же», и так далее. Разумеется, акут надо ставить только в том случае, когда возможны разночтения. Ина́че э́то бу́дет похо́же на де́тский буква́рь. Знак ударения, естественно, ставится над ударной буквой. Символ U+0301 при наборе ставится после гласной, на которую падает ударение, как и любой другой комбинирующийся символ Unicode. |
Как многие, наверное, успели заметить, шрифт Verdana от Microsoft и с акутом не дружит, размещая его над следующим, а не над предыдущим символом. Я не знаю, есть ли подобная проблема в MacOS или *nix. Будем надеяться, что она отомрёт со временем.
Вообще говоря, проблема решается обновлением шрифта до версии 5.01, Verdana этой версии правильно обрабатывает диакритики. Для обновления можно скачать European Union Expansion Font Update, который доводит Verdana до версии 5.01 и решает проблему в Windows XP и Vista. Также приведу ссылку на скачивание отдельно шрифта Verdana 5.01 в формате TTF.
Знаки минуты и секунды (они же — фута и дюйма)
Возможно, в связи с проникновением компьютерных технологий в современную жизнь и общей глобализацией, одинарный и двойной штрихи приживутся в качестве сокращений для фута и дюйма в тесном наборе, но в обычных текстах я рекомендую писать слова «фут» и «дюйм» полностью.
Значение слова «штрих»
1. Черта, линия, являющаяся одним из основных элементов рисунка. Вахнов в несколько штрихов красиво нарисовал ему большой, выпуклый, с шишкой нос. Гарин-Михайловский, Детство Темы.
2. перен.; обычно с определением. Отдельная подробность, черта, сторона чего-л. Теперь для него было ясно все, до последнего штриха; его женитьбу на Зосе устроил не кто другой, как тот же Половодов. Мамин-Сибиряк, Приваловские миллионы. По-настоящему раскрывалась Савина только на спектакле. Несколькими характерными штрихами она создавала облик изображаемого лица. Мичурина-Самойлова, Шестьдесят лет в искусстве.
Источник (печатная версия): Словарь русского языка: В 4-х т. / РАН, Ин-т лингвистич. исследований; Под ред. А. П. Евгеньевой. — 4-е изд., стер. — М.: Рус. яз.; Полиграфресурсы, 1999; (электронная версия): Фундаментальная электронная библиотека
Штрих — графический символ и типографский знак в виде короткой наклонной черты у верхнего края строки, например:
Штрих в музыке — способ извлечения звука;
Штрих Шеффера — одна из бинарных логических операций (2И-НЕ).
ШТРИХ, а́, м. [нем. Strich]. 1. Тонкая черта, линия. Ш. на бумаге. Штрихами на планах изображается рельеф местности. Портрет был почти совсем готов; оставалось докончить лицо несколькими штрихами. Тургенев. 2. перен. Характерная черта, сторона чего-н. Добавить еще один ш. к характеристике.
Источник: «Толковый словарь русского языка» под редакцией Д. Н. Ушакова (1935-1940); (электронная версия): Фундаментальная электронная библиотека
штрих
1. короткая черта, линия (в рисунке, чертеже и т. п.)
2. перен. отдельная подробность, характерный момент чего-либо ◆ Вместе с этим здесь надо отметить ещё один штрих, чрезвычайно важный для понимания органологии образов в поэзии Блока. А. Белый, «Доклад на Открытом заседании Вольной Философской Ассоциации», 1921 г. (цитата из НКРЯ)
3. матем. знак, идущий после переменных, функций и других обозначений в математических и физических обозначениях
4. разг. устар. канцелярский корректор, средство, с помощью которого осуществляется исправление ошибок в тексте, корректировка написанного на бумаге. ◆ Если этого нет — тогда не образ Божий, но ошибка природы, огреха, которую нужно стереть, как «штрих» стирает неверно напечатанную букву, или, ещё точнее, как компьютер стирает неверно написанную строку. О. Г. Щербинина, «Архетип веры», 1998 г.
Делаем Карту слов лучше вместе

Спасибо! Я обязательно научусь отличать широко распространённые слова от узкоспециальных.
Насколько понятно значение слова задёргать (глагол), задёргал: