Как называется объемный прямоугольник в геометрии
Прямоугольный параллелепипед. Что это такое?
Определение параллелепипеда
Начнем с того, что узнаем, что такое параллелепипед.
Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.
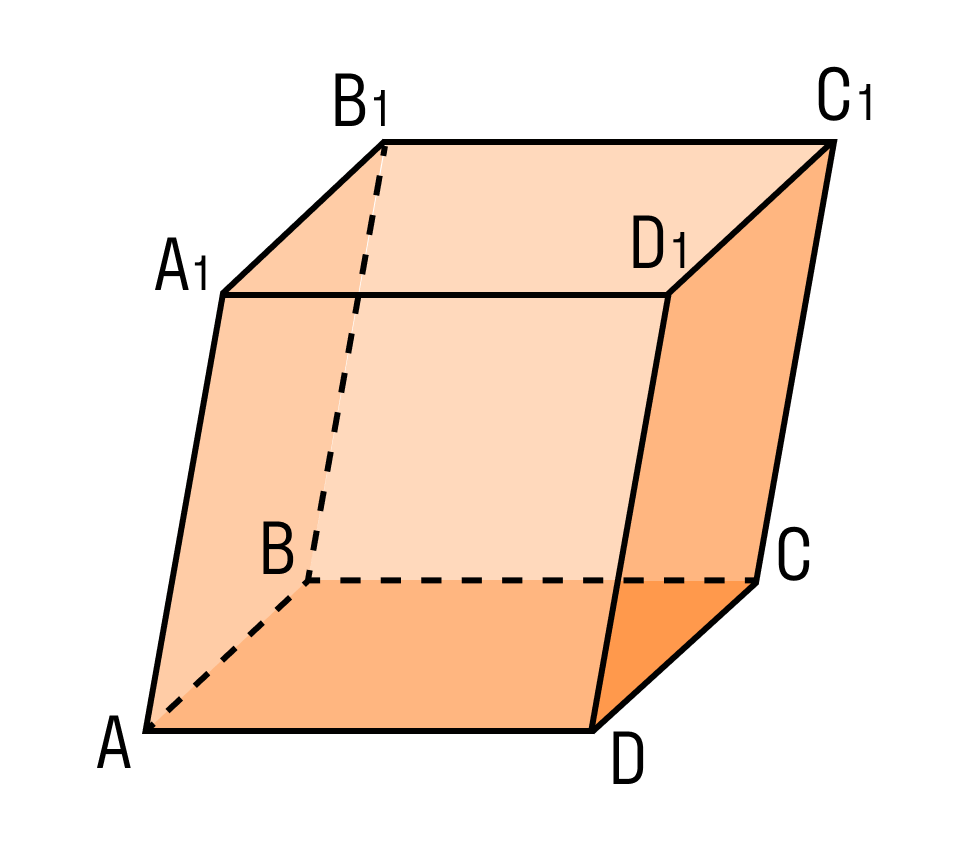
На рисунке два параллелограмма АВСD и A1B1C1D1. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA1, ВB1, CC1, DD1 параллельны друг другу. Образовавшаяся фигура — параллелепипед.
Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.
Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.
Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.
Параллелепипед — это:
Свойства параллелепипеда
Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.
Вот 4 свойства параллелепипеда, которые необходимо запомнить:
Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.
Прямой параллелепипед
Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.
Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.
Свойства прямого параллелепипеда:
На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.
Формулы прямого параллелепипеда:
Прямоугольный параллелепипед
Определение прямоугольного параллелепипеда:
Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.
Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.
Свойства прямоугольного параллелепипеда
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.
Формулы прямоугольного параллелепипеда:
Диагонали прямоугольного параллелепипеда: теорема
Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.
Если есть теорема, нужно ее доказать. (с) Пифагор
Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
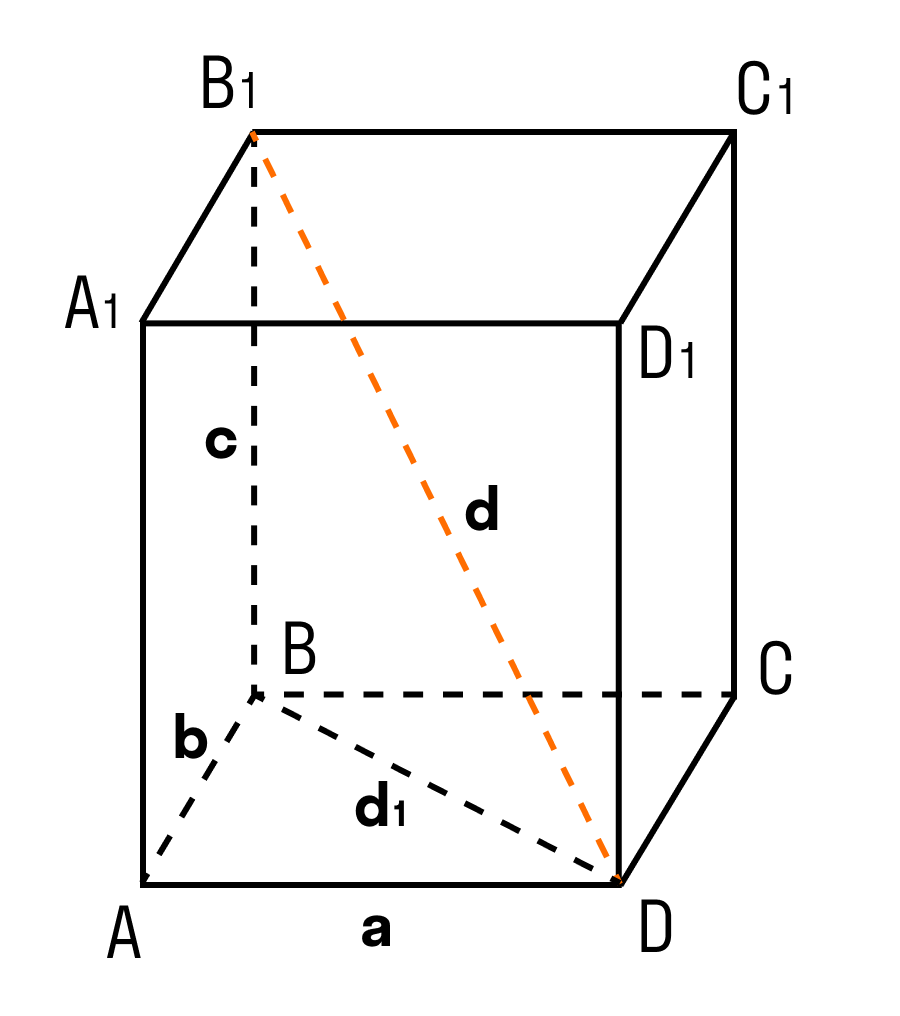
В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.
Дан прямоугольный параллелепипед ABCDA1B1C1D1. Доказать теорему.
Доказательство теоремы:
Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.
Все грани прямоугольного параллелепипеда — прямоугольники.
ΔABD: ∠BAD = 90°, по теореме Пифагора
ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора
d² = a² + b² + c²
Доказанная теорема — пространственная теорема Пифагора.
Куб: определение, свойства и формулы
Кубом называется прямоугольный параллелепипед, все три измерения которого равны.
Каждая грань куба — это квадрат.
Свойства куба:
Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.
Формулы куба:
Решение задач
Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.
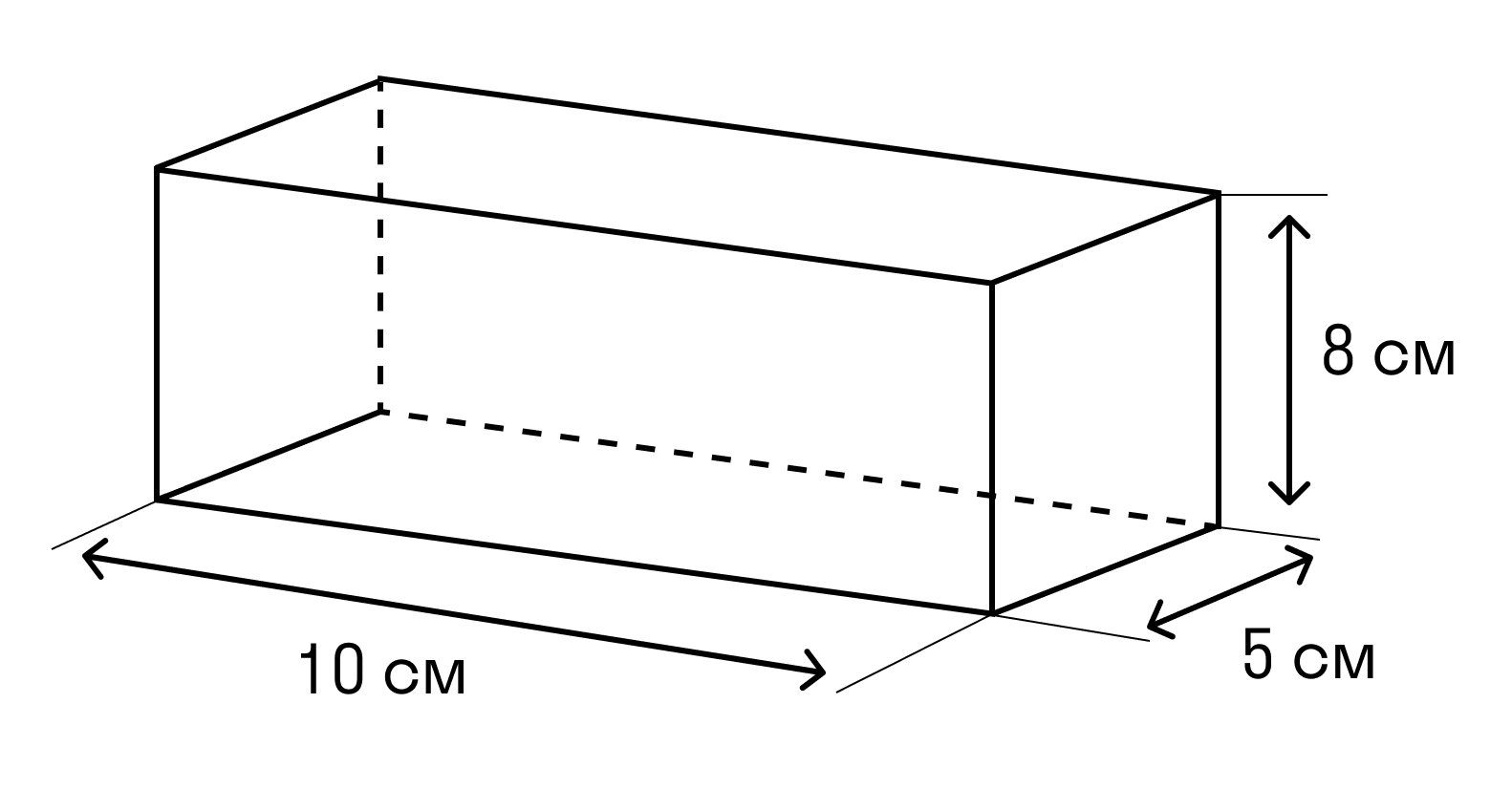
Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.
Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.
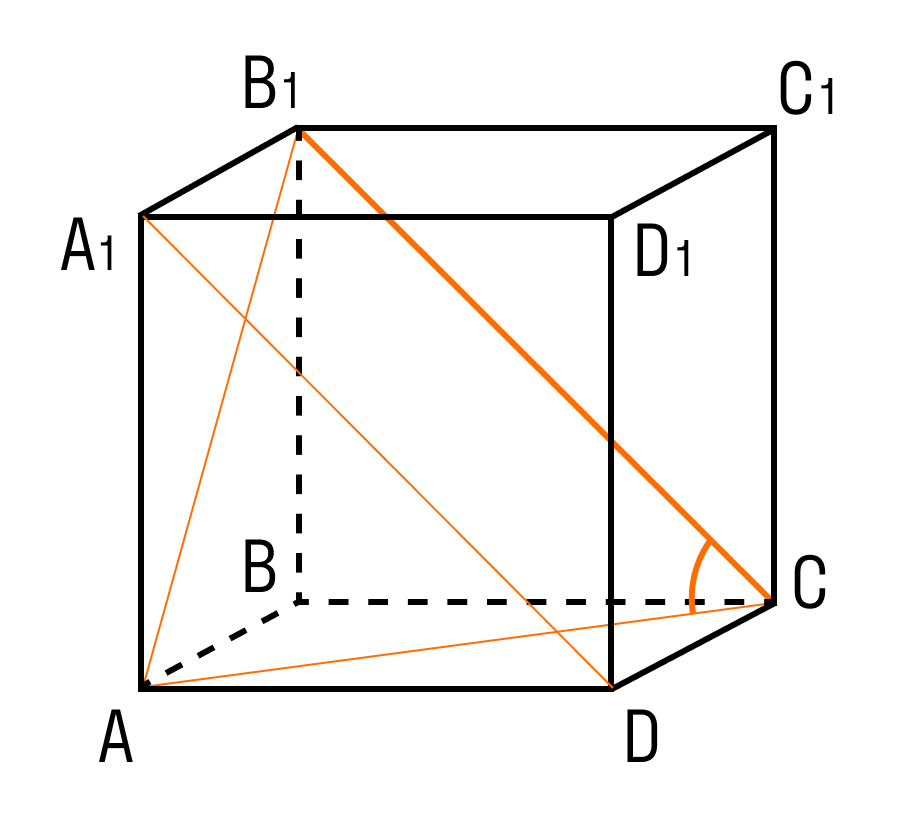
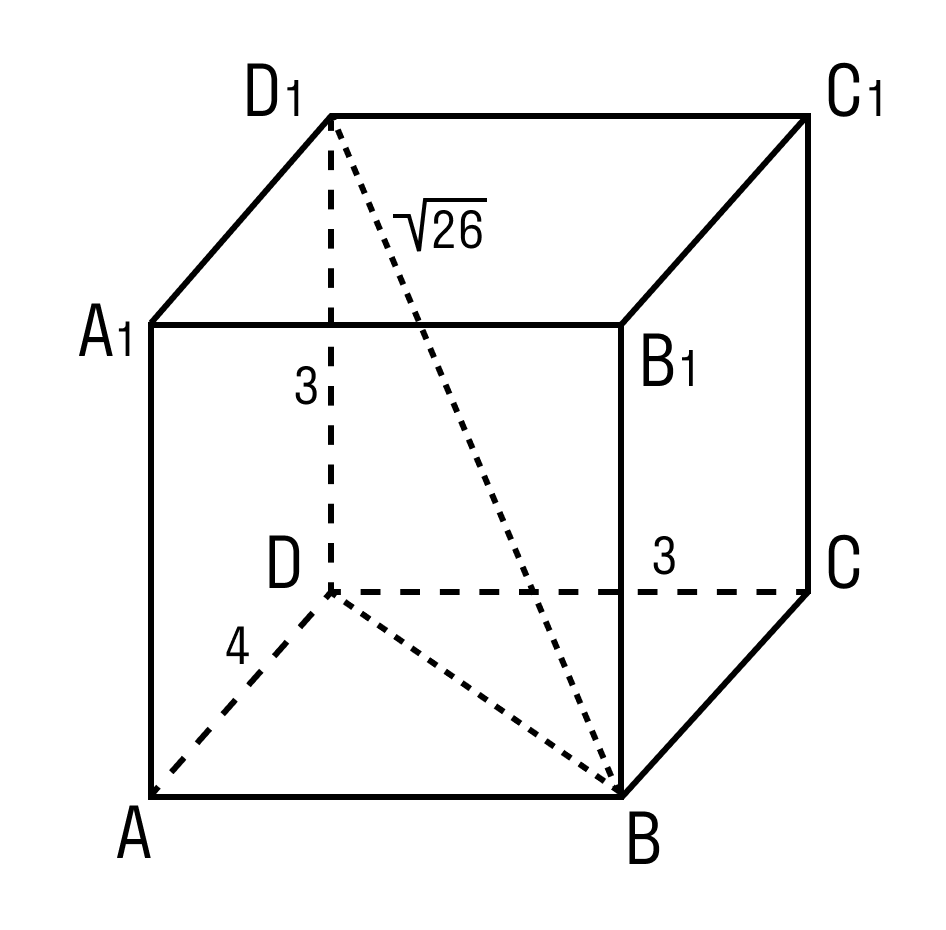
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Нужно найти длину ребра A1B1.
В фокусе внимания треугольник BDD1.
Угол D = 90°.
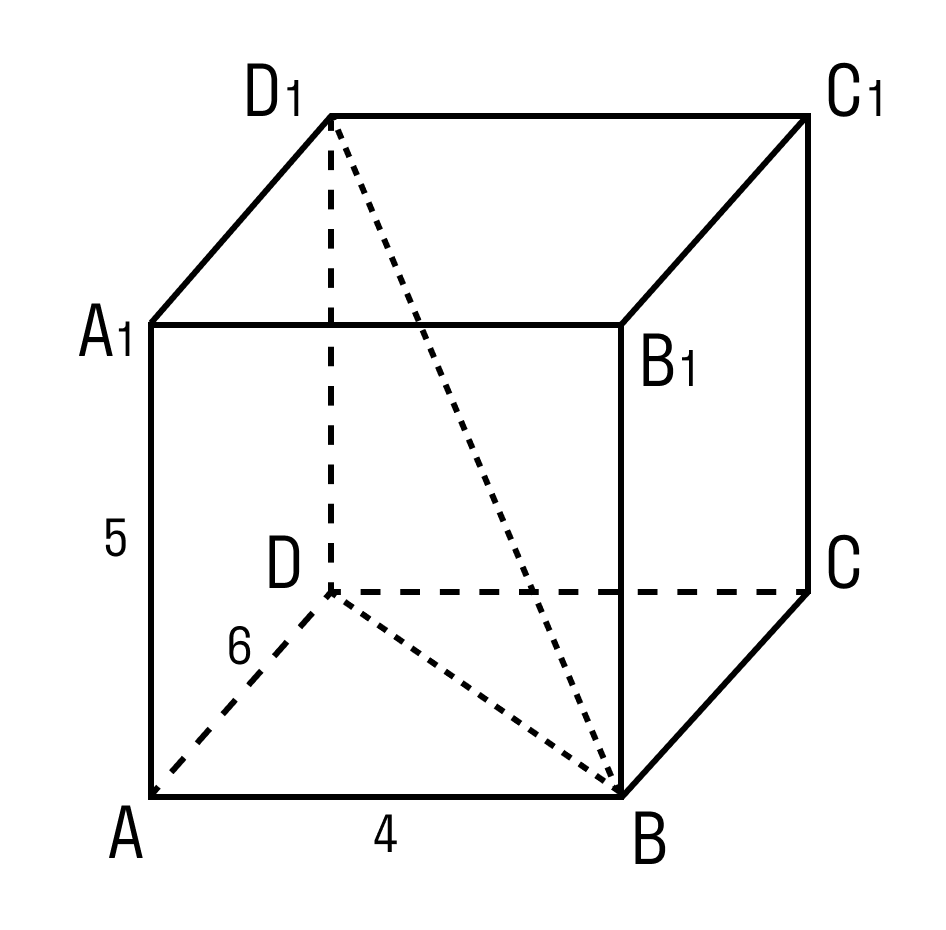
Задачка 3. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
AB = 4
AD = 6
AA1= 5
Нужно найти отрезок BD1.
В треугольнике ADB угол A = 90°.
По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD1 угол D = 90°.
BD1 2 = 52 + 25 = 77
BD1 = √77.
Самопроверка
Теперь потренируйтесь самостоятельно — мы верим, что все получится!
Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.
Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.
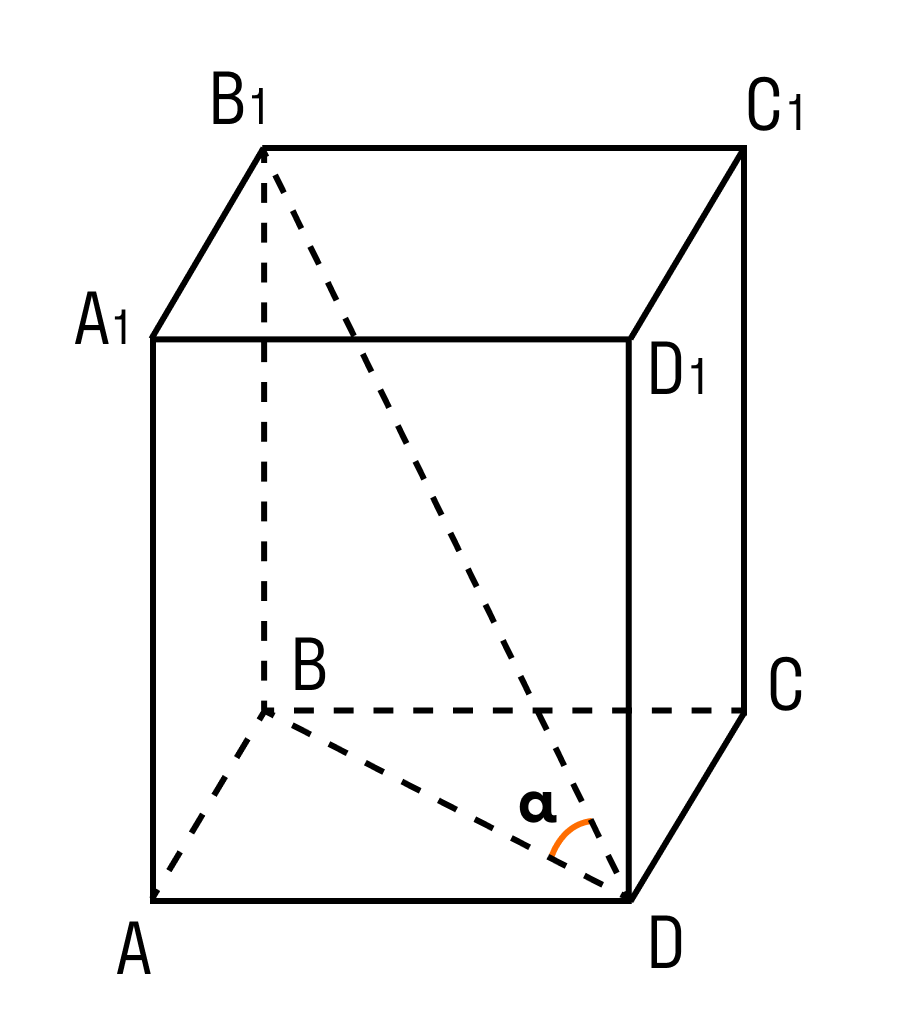
Задачка 2. Дан прямоугольный параллелепипед АВСDA1B1C1D1.
Вычислите длину ребра AA1.
Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:
Урок 29 Бесплатно Прямоугольный параллелепипед
На прошлых занятиях мы рассматривали плоские фигуры.
В реальности же каждый предмет, какой бы он формы не был, занимает некоторую часть пространства.
Даже у самого тонкого листа бумаги имеется толщина.
Если взять стопку таких листов, то объем стопки бумаги будет хорошо заметен.
Раздел геометрии, в котором изучаются фигуры и их свойства в пространстве, называется стереометрией.
Слово стереометрия происходит от древнегреческого «стериос»- объемный, пространственный и «метрио»- измерять.
Базовыми фигурами в пространстве, как и на плоскости, является точка, прямая и плоскость, из которых образуются объемные геометрические фигуры, тела, пространства.
Геометрическое тело, состоящее из плоских многоугольников, называют многогранником.
Существует огромное множество многогранников: выпуклые, невыпуклые, правильные и т.д.
На данном уроке познакомимся с выпуклым прямоугольным многоугольником, который называется параллелепипед.
Выясним, как прямоугольный параллелепипед выглядит и из каких элементов он состоит.
Рассмотрим его свойства.
Научимся изображать данный многоугольник на плоскости и вычислять площадь его поверхности.
Разберем несколько примеров решения задач.
Прямоугольный параллелепипед
Каждый может себе представить и знает, как выглядят детские кубики.
С кубиками и конструктором из брусочков прямоугольной формы многие знакомы с раннего детства: строили домики, башенки, дороги, затем все это радостно рушили.
Всем известно, как выглядит коробка конфет или долька шоколада. Многие получали подарки в красивой красочной коробке с ярким бантом, читали книги с увлекательными рассказами и сказками.
Если обратим внимание на форму, то заметим, что все изображенные объекты имеют некоторое сходство, они представляют собой прямоугольный параллелепипед.
Прямоугольный параллелепипед-это объемная геометрическая фигура, многогранник, состоящий из шести прямоугольников.
Плоские фигуры, такие как квадрат, прямоугольник, треугольник изобразить на плоскости легко, они являются её частью.
Любую объемную фигуру изобразить на плоскости затруднительно.
Многогранник необходимо изобразить так, чтобы была заметна объемность фигуры.
Пунктирная линия дает возможность понять наблюдателю, как расположен многогранник и определить, откуда необходимо смотреть на него.
Если мы изобразим параллелепипед только сплошной линией, то на рисунке будут изображены различные четырехугольники, соединенные между собой, а объемного представления многоугольника данный рисунок не даст.
Даже если нам известно, что изображен прямоугольный параллелепипед, то все равно непонятно какой стороной расположен многогранник к наблюдателю.
Если невидимые линии на рисунке изобразить пунктирными линиями, то у фигуры сразу будет заметен объем.
Прямоугольный параллелепипед изображают так:
Прямоугольники, из которых состоит прямоугольный параллелепипед, называют гранями, причем противоположные грани его попарно равны.
Верхняя грань равна нижней, правая равна левой, передняя грань равна задней.
Грань, на которой стоит прямоугольный параллелепипед, называют нижним основанием, противоположную грань называют верхним основанием параллелепипеда.
Остальные четыре грани называют боковыми гранями.
Стороны граней называют ребрами параллелепипеда.
Концы ребер, т.е. вершины граней, называют вершинами параллелепипеда.
На рисунке вершины изображены точками.
У меня есть дополнительная информация к этой части урока!
Для любого выпуклого многогранника, в том числе и для параллелепипеда, справедливо утверждение: Г + В – Р = 2, где
Г— число граней
В— число вершин
Р— число ребер
Данное утверждение говорит о том, что количество вершин и граней многоугольника вместе взятых всегда на два больше количества ребер.
Это правило называют теоремой Эйлера в честь ее создателя математика, механика Леонарда Эйлера.
Проверим справедливость теоремы Эйлера для разных фигур.
Параллелепипед состоит из следующих элементов: 6 граней (Г = 6), 8 вершин (В = 8), 12 ребер (Р = 12).
Г + В – Р = 6 + 8 – 12 = 14 – 12 = 2
Получили верное равенство.
Пирамида- это многогранник, в основании которого лежит многоугольник.
Грани пирамиды- это треугольники, сходящиеся в общую вершину.
Тетраэдр- пирамида, состоящая из 4 граней- равных треугольников (Г = 4), 4 вершин (В = 4) и 6 ребер (Р = 6).
Г + В – Р = 4 + 4 – 6 = 8 – 6 = 2
Получили верное равенство.
Четырехугольная пирамида имеет 5 граней: квадрат в основании и 4 треугольника в качестве боковых граней (Г = 5), 5 вершин (В = 5), 8 ребер (Р = 8).
Г + В – Р = 5 + 5 – 8 = 10 – 8 = 2
Получили верное равенство
Прямоугольный параллелепипед имеет три линейные величины (три измерения): ширину, длину и высоту.
Величину прямоугольного параллелепипеда определяют длинами трех ребер, исходящих из одной вершины.
Если все три величины прямоугольного параллелепипеда равны, то такой параллелепипед называют кубом.
Куб по-другому называют правильный гексаэдр (от греческого «hex»- шесть и «hedra»- грань).
Он имеет все те же элементы, что и прямоугольный параллелепипед.
Все шесть граней куба равны, следовательно, и все 12 ребер между собой равны.
У меня есть дополнительная информация к этой части урока!
Куб относится к Платоновским телам.
Платоновскими телами называют объемные геометрические тела выпуклой формы, которые состоят из одинаковых по форме и размеру многоугольников, а в каждой вершине такого многогранника сходится одинаковое число ребер.
Всего существует пять Платоновских тел. Такие многогранники известны с древних времен.
В Древней Греции существовали различные философские школы, в которых пытались разъяснить существование и выяснить предназначение геометрических тел правильной формы.
Пифагорейцы считали, что материя состоит из четырех составляющих: огня, воды, воздуха, земли.
Ассоциировали четыре правильных многогранника (тетраэдр, гексаэдр, октаэдр, икосаэдр) с этими стихиями.
Пятый правильный многогранник (додекаэдр) олицетворял все мироздание, Вселенную, его стали называть «пятая сущность».
Учения Пифагорейцев изложил в своих трудах древнегреческий философ, ученый Платон. В связи с этим правильные многогранники стали называть Платоновскими телами.





Число и вид граней
Число ребер, сходящихся в вершине
Пройти тест и получить оценку можно после входа или регистрации
Площадь поверхности прямоугольного параллелепипеда
Если посмотреть вокруг, то мы можем заметить огромное множество объектов, имеющих форму прямоугольного параллелепипеда или напоминающих его форму.
Так, например, большинство зданий и помещений, шкаф (тумбочка), столешница, аквариум, коробка, кирпичи и многое другое представляют собой прямоугольный параллелепипед.
Такой многогранник имеет широкое применение в различных областях нашей жизни, и это неспроста:
1) прямоугольная форма параллелепипеда удобна для деления целого на части
2) объекты прямоугольной формы легко надстраивать и совмещать
3) прямоугольный параллелепипед является одним из самых устойчивых многогранников
Часто приходится определять площадь поверхности объекта, имеющего форму прямоугольного параллелепипеда.
Давайте разберемся, как и с помощью каких формул можно вычислить площадь его поверхности.
Допустим, у нас есть коробка, имеющая форму прямоугольного параллелепипеда.
Попробуем изобразить развертку данного геометрического тела.
Площадь этой развертки- это и есть площадь поверхности прямоугольного параллелепипеда.
Так как прямоугольный параллелепипед состоит из шести граней, имеющих форму прямоугольников, причем противоположные грани равны по величине, то площадь поверхности прямоугольного параллелепипеда будет равна сумме площадей всех его шести граней.
Пусть для нашего прямоугольного параллелепипеда три ребра, выходящие из одной вершины, имеют значения а, b, h.
а— ширина прямоугольного параллелепипеда
b— длина прямоугольного параллелепипеда
h— высота прямоугольного параллелепипеда
Найдем площадь всех граней.
Воспользуемся формулой для расчета площади прямоугольника: площадь прямоугольника равна произведению его ширины на длину.
Ребра, лежащие напротив ребер а, b, h, будут иметь такие же значения длины, так как противолежащие ребра прямоугольного параллелепипеда равны.
В таком случае получаем:
1) Площадь нижнего основания равна произведению (a ∙ b)
2) Площадь верхнего основания также равна произведению (a ∙ b)
3) Площадь левой боковой и правой боковой граней равны, как противолежащие, площадь каждой из них определяется произведением (b ∙ h)
4) Передняя и задняя боковые грани равны, а значение площади каждой из них будет определяться произведением (а ∙ h)
Сложим площади всех граней прямоугольного параллелепипеда, получим общую площадь его поверхности.
Упростим выражение, вынесем 2 за скобку.
Формула площади поверхности прямоугольного параллелепипеда будет выглядеть так:
Площадь двух оснований прямоугольного параллелепипеда (это два прямоугольника) найдем по формуле:
Sосн = 2 (a ∙ b).
Площадь боковой поверхности прямоугольного параллелепипеда можно найти по формуле:
Sбок = 2h ∙ (a + b).
В нашем случае а, b— это стороны основания, h— это высота прямоугольного параллелепипеда (боковое ребро).
Так как основанием прямоугольного параллелепипеда является прямоугольник, то периметр основания прямоугольного параллелепипеда определяется равенством
Роснов = 2 ∙ (a + b).
Подставим Роснов в формулу Sбок = 2h ∙ (a + b) вместо выражения 2 ∙ (a + b).
Тогда площадь боковой поверхности можно найти так:
Sбок = Роснов ∙ h.
Определим площадь поверхности куба.
Чтобы найти площадь поверхности куба, необходимо сложить площади всех его граней.
Площадь одной грани куба найдем по формуле площади квадрата:
S = a 2
а— это сторона квадрата (ребро куба).
Так как все 6 граней куба представляют собой равные по площади квадраты, следовательно, чтобы найти площадь всей поверхности куба, необходимо площадь одной грани умножить на их количество.
Формула площади поверхности куба выглядит так:
Рассмотрим решение нескольких практических задач.
В процессе любого строительства или ремонта очень часто встает вопрос о том, сколько необходимо потратить строительного и отделочного материала или как рассчитать расход краски.
Задача №1.
Какое количество краски понадобится, чтобы полностью покрасить бак прямоугольной формы?
Ширина бака 2 метра, длина 3 метра, высота 1 метр.
Известно, что на 1 м 2 расходуется 200 г краски.
Чтобы рассчитать количество краски, которое нужно затратить на покраску бака, необходимо определить площадь окрашиваемой поверхности, затем, зная норму расхода краски на единицу площади, можно рассчитать расход краски на всю окрашиваемую поверхность.
Пусть m1— масса краски, которая расходуется на 1 м 2
m2— масса краски, которая необходима для покраски всего бака.
Задача №2
Сколько квадратных метров стекла понадобится на изготовление аквариума кубической формы длиной 100 см?
Для вычисления площади поверхности аквариума в квадратных метрах необходимо длину аквариума перевести из сантиметров в метры.
Вспомним, 1 м = 100 см.
Если бы аквариум необходимо было изготовить только из боковых стенок и основания, то из стекла пришлось бы вырезать всего 5 квадратных граней.
В таком случае формула для вычисления площади поверхности аквариума приняла бы вид
Задача №3
Хозяйка решила покрасить стены в комнате.
Комната имеет форму прямоугольного параллелепипеда.
Ширина комнаты 3 метра, длина комнаты 4 метра, высота комнаты 3 метра.
Пусть Sc— общая площадь стен комнаты.
Sд— площадь дверного проема.
Sо— площадь оконного проема.
S— площадь стен комнаты за исключением площади дверного и оконного проемов.
Пройти тест и получить оценку можно после входа или регистрации
Геометрические фигуры. Параллелепипед.
Параллелепипед — призма, основанием которой является параллелограмм либо (равносильно) многогранник с шестью гранями, являющимися параллелограммами. Шестигранник.
Параллелограммы, из которых состоит параллелепипед являются гранями этого параллелепипеда, стороны этих параллелограммов являются ребрами параллелепипеда, а вершины параллелограммов — вершинами параллелепипеда. У параллелепипеда каждая грань является параллелограммом.
Как правило выделяют любые 2-е противолежащие грани и называют их основаниями параллелепипеда, а оставшиеся грани — боковыми гранями параллелепипеда. Ребра параллелепипеда, которые не принадлежат основаниям являются боковыми ребрами.
2 грани параллелепипеда, которые имеют общее ребро являются смежными, а те, которые не имеют общих ребер — противоположными.
Отрезок, который соединяет 2 вершины, которые не принадлежат 1-ой грани является диагональю параллелепипеда.
Длины ребер прямоугольного параллелепипеда, которые не параллельны, являются линейными размерами (измерениями) параллелепипеда. У прямоугольного параллелепипеда 3 линейных размера.
Типы параллелепипеда.
Существует несколько видов параллелепипедов:
Прямым является параллелепипед с ребром, перпендикулярным плоскости основания.
Прямой параллелепипед с прямоугольником в основании является прямоугольным параллелепипедом. У прямоугольного параллелепипеда каждая из граней является прямоугольником.
Наклонный параллелепипед — это параллелепипед, у которого боковые грани расположены, по отношению к основаниям, под углом, не равным 90 градусов.
Прямоугольный параллелепипед, у которого все 3 измерения имеют равную величину, является кубом. Каждая из граней куба – это равные квадраты.
Произвольный параллелепипед. Объём и соотношения в наклонном параллелепипеде в основном определяются при помощи векторной алгебры. Объём параллелепипеда равняется абсолютной величине смешанного произведения 3-х векторов, которые определяются 3-мя сторонами параллелепипеда (которые исходят из одной вершины). Соотношение между длинами сторон параллелепипеда и углами между ними показывает утверждение, что определитель Грама данных 3-х векторов равняется квадрату их смешанного произведения.
Свойства параллелепипеда.
В параллелепипед вписывают тетраэдр. Объем этого тетраэдра будет равняться третьей части объема параллелепипеда.