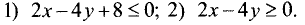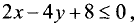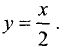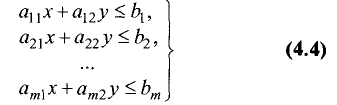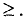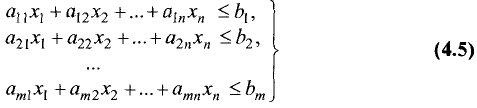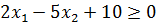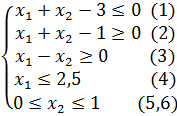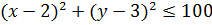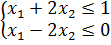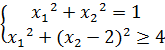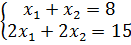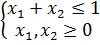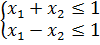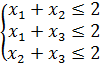Как называется множество точек плоскости
Выпуклые множества точек и их свойства с примерами решения и образцами выполнения
Основные определения:
Множество точек называется выпуклым, если оно вместе с любыми
двумя своими точками содержит весь отрезок, соединяющий эти точки.
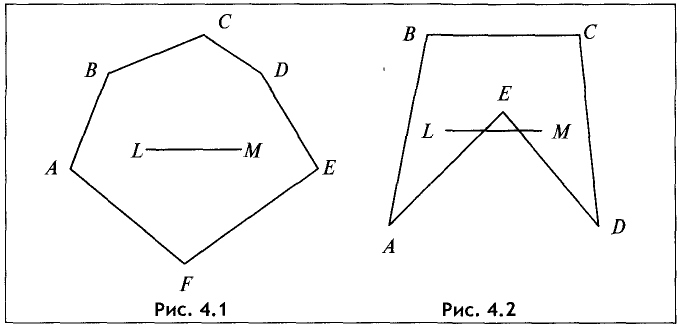
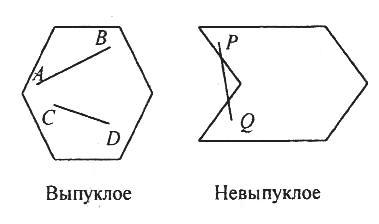
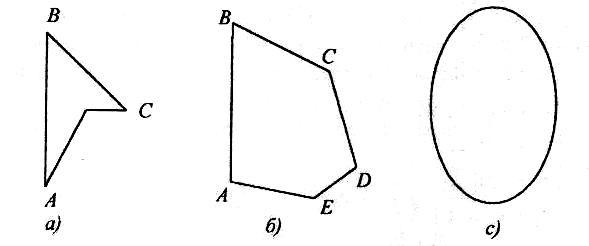
Например, многоугольник, представленный на рис. 4.1,
является выпуклым, а многоугольник на рис.4.2 выпуклым не является.
Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются прямая, круг, куб,
многогранная область, полуплоскость, полупространство и т.д.
Пересечение любого числа выпуклых множеств есть выпуклое
множество.
Точка множества называется внутренней, если в любой ее окрестности (например, круг или шар с центром в этой точке) содержатся точки только данного множества.
Точка множества называется граничной, если в любой ее окрестности содержатся как точки, принадлежащие данному множеству, так и точки, не принадлежащие ему.
Точка множества называется угловой (крайней), если она не является внутренней ни для какого отрезка, целиком принадлежащего данному множеству.
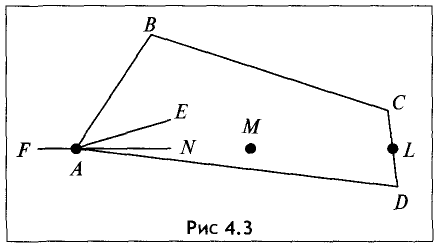
Примеры угловой А, внутренней L и граничной М точек приведены на рис. 4.3.
Точка А является угловой, так как для любого отрезка АЕ,
целиком принадлежащего многоугольнику, она не является
внутренней. Точка А — внутренняя для отрезка FN, но этот отрезок не принадлежит целиком множеству.
Для выпуклого множества угловые точки всегда совпадают с вершинами многоугольника (многогранника).
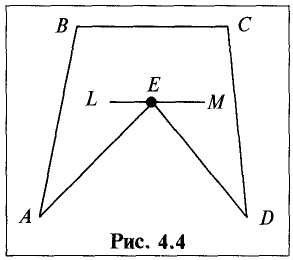
Так, на рис. 4.4 точка Е является вершиной невыпуклого многоугольника, но не является угловой, так как она является внутренней для отрезка LM, целиком принадлежащего этому
многоугольнику.
Множество точек называется замкнутым, если оно включает все свои граничные точки.
Множество точек называется ограниченным, если существует круг (шар) радиуса конечной длины с центром в любой точке множества, который полностью содержит в себе данное множество. В противном случае множество называется неограниченным.
Выпуклое замкнутое множество точек плоскости (пространства), имеющее конечное число угловых точек, называется выпуклым многоугольником (многогранником), если оно ограниченное, и выпуклой многоугольной (многогранной) областью, если оно неограниченное.
Введенные понятия рассматривались для множества точек на
плоскости и в пространстве. Их можно обобщить также на n-мерное
точечное пространство.
Геометрический смысл решений неравенств
Рассмотрим решения неравенств с двумя переменными типа
Теорема:
Множество решений неравенств с двумя переменными (4.1) является одной из двух полуплоскостей, на которые вся плоскость делится прямой
включая и эту прямую, а другая полуплоскость — множеством решений неравенства
Пример:
Построить график множества решений следующих
неравенств:
Решение:
В соответствии с теоремой множество решений
приведенных неравенств есть полуплоскость.
1.Границей первой полуплоскости является прямая
Представим уравнение этой прямой в виде 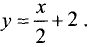
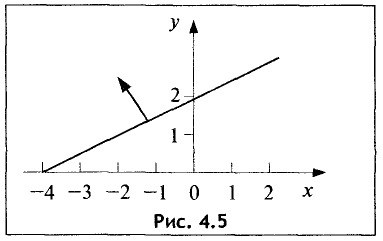
Ее график представлен на рис. 4.5.
Для определения искомой полуплоскости зададим произвольную контрольную точку, не лежащую на построенной прямой. Проще всего задать точку с координатами (0; 0). Подставив данные
координаты в неравенство
видим, что оно не выполняется, так как 8 > 0. Поэтому искомой является верхняя полуплоскость.
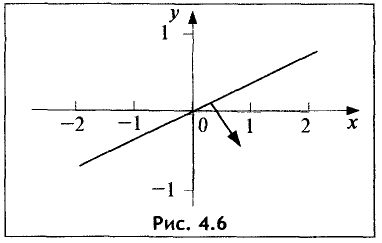
2.Границей второй полуплоскости является прямая
Представим это уравнение в виде
График исследуемой прямой представлен на рис. 4.6.
В данном случае точка с координатами (0; 0) лежит на этой
прямой. Поэтому выбираем точку с координатами (0; —1) и подставляем данные координаты в неравенство 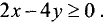
Основные свойства выпуклого множества точек
Рассмотрим множество решений совместной системы линейных
неравенств с двумя переменными.
Теорема:
Множество решений совместной системы т линейных
неравенств с двумя переменными
является выпуклым многоугольником (или выпуклой многоугольной областью).
Знаки некоторых или всех неравенств могут быть
Эту теорему для n переменных можно сформулировать
следующим образом.
Теорема:
Множество решений совместной системы m линейных
неравенств с n переменными
является выпуклым многогранником (или выпуклой многогранной областью) в n-мерном пространстве.
Пересечение полуплоскостей, каждая из которых определяется соответствующим неравенством системы, называется областью решения системы.
Область решений системы, удовлетворяющая условиям неотрицательности 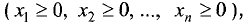
Пример:
Построить область решений и область допустимых
решений системы неравенств и определить координаты угловых точек области допустимых решений:
Решение:
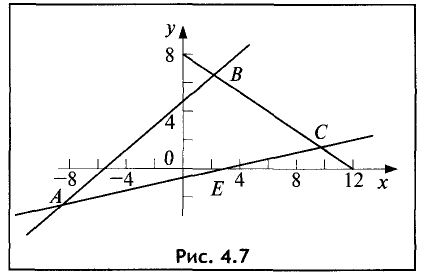
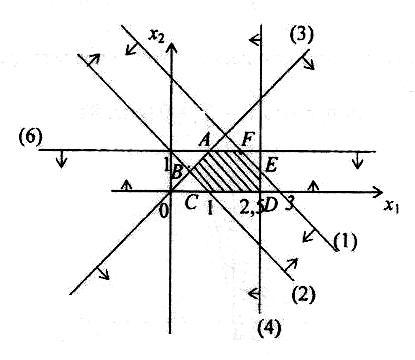
Областью решений является треугольник ABC, представленный на рис. 4.7.
Для нахождения искомой полуплоскости зададим контрольную
точку с координатами (0; 0). Подставив данные координаты в неравенство 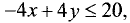
Образовательный сайт для студентов и школьников
Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.
© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института
Множество точек. Изображение некоторых множеств точек на плоскости.
В первом случае прямые параллельны оси ординат, во втором – абсцисс.
На координатной прямой неравенству х 3. Проанализируем, что это за точки:
— множество точек, абсцисса которых больше или равна 3
— точки, лежащие правее прямой х = 3 и на прямой.
Алгоритм построения будет иметь вид:
— строим в координатной плоскости прямую: х = 3;
— определяем, где будут находиться точки, абсцисса которых больше 3; ответ – правее;
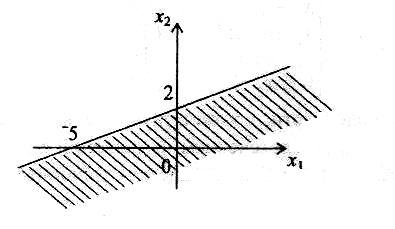
— множество всех точек удовлетворяющих условию х > 3 покажем при помощи штриховки;
х > 3 задает полуплоскость, находящаяся правее прямой х = 3 и все точки этой прямой. Прямую изображаем одной цельной линией, этим указываем, что все точки расположенные на прямой так же включены во множество.
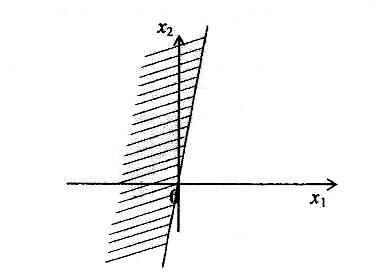
Представим множество точек, удовлетворяющих условию у 1.
Следовательно, они будут находиться выше прямой у = 1. В соответствии со знаком неравенства точки прямой у = 1 не удовлетворяют условию y > 1. Графически мы это покажем, изобразив прямую у = 1 пунктиром.
Представим множество точек, соответствующих условию у > 1 так:
Множество точек плоскости равноудалённых от некоторой точки, как называется эта точкаА?
Множество точек плоскости равноудалённых от некоторой точки, как называется эта точка
Так как множеством точек плоскости, равноудаленных от некоторой точки является окружность, то данная точка является ее центром.
Возьмите на удачу четыре точки на плоскости ху?
Возьмите на удачу четыре точки на плоскости ху.
Найдите координаты этих точек.
Точка О – центр окружности, описанной около треугольника АВС?
Точка О – центр окружности, описанной около треугольника АВС.
Принадлежит ли точка С плоскости, в которой лежат точки А, В и О?
Найдите на оси х точку, равноудалённую от точек (1 ; 2) и (2 ; 3)объясните понятным языком?
Найдите на оси х точку, равноудалённую от точек (1 ; 2) и (2 ; 3)
объясните понятным языком.
Начертите окружность с центром в точке О и радиусом r = 3, 5 см?
Начертите окружность с центром в точке О и радиусом r = 3, 5 см.
Проведите диаметр и радиусы разноцветными карандашами
с картинкой с разноцветными карандашами плз.
Две окружности касаются в точке С?
Две окружности касаются в точке С.
Найдите градусную меру угла бетта.
ПОМОГИТЕ СРОЧНО Начертите окружность с центром O и радиус 2см?
ПОМОГИТЕ СРОЧНО Начертите окружность с центром O и радиус 2см.
Отметьте на ней точку M.
Найдиье на окружности точки, находящиеся от точки М на расстоянии : а)2см, б)4см.
Отметьте эти точки и соедините их отрезками с точкой M.
Сколько при этом образовалось отрезков?
На каком из этих лежит центр окружности О?
Две окружности радиуса 4 см и 6 см имеют общий центр ( их называют концентрическими окружностями )?
Две окружности радиуса 4 см и 6 см имеют общий центр ( их называют концентрическими окружностями ).
Найдите расстояние между наиболее удаленными точками этих окружностей.
AM = MB, AB = AM + MB = > AM / AB = 1 / 2 ME⊥AC △MEA
15 градусов ыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыыы.
Прямые а ибо перпендикулярны. Через точку их пересечения проведена прямая с. Определите число получившийся при этом тупыхуглов Всего их 4.
А) AB = CD AD = BC б)СD и AB в) надо измерять, скорее всего AD = BC. AB = CD.
Множество точек на координатной плоскости
Просмотр содержимого документа
«Множество точек на координатной плоскости»
Урок алгебры в 9 классе
Ни одна наука так не укрепляет веру в силу человеческого разума, как математика.
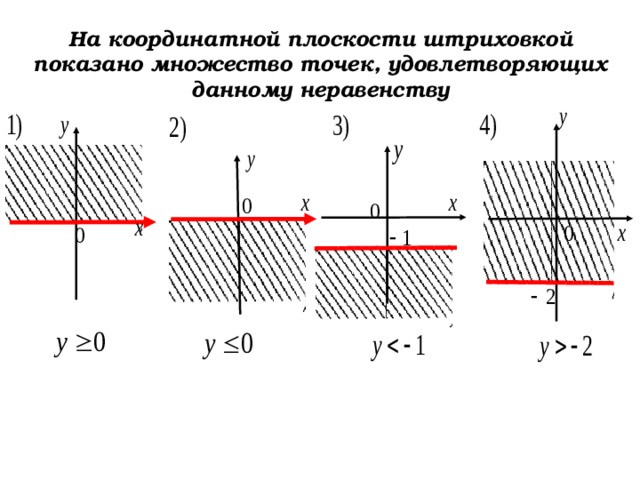
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
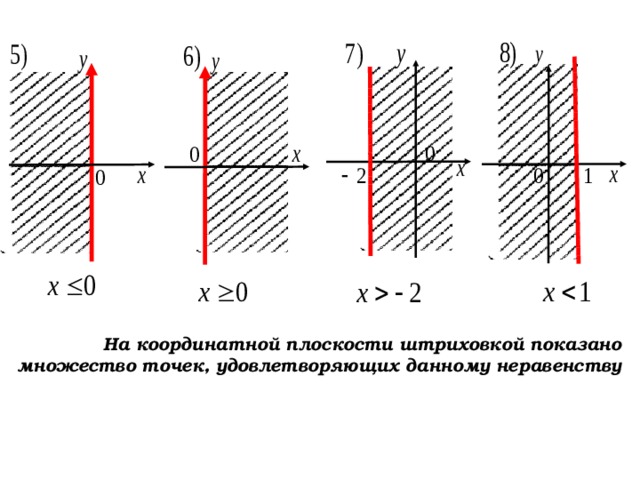
На координатной плоскости штриховкой показано множество точек, удовлетворяющих данному неравенству
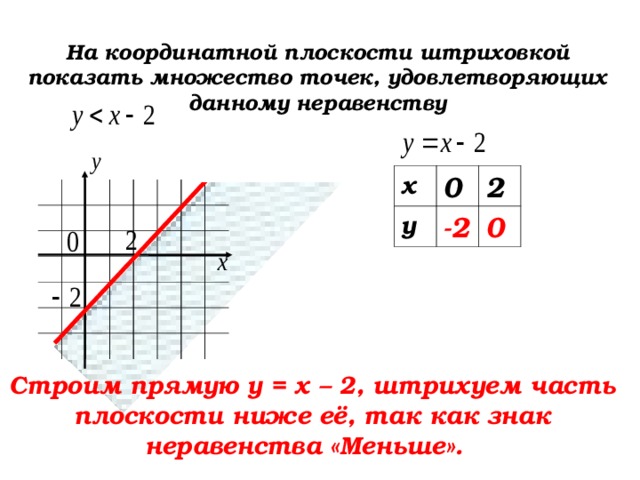
На координатной плоскости штриховкой показать множество точек, удовлетворяющих данному неравенству
Строим прямую у = х – 2, штрихуем часть плоскости ниже её, так как знак неравенства «Меньше».
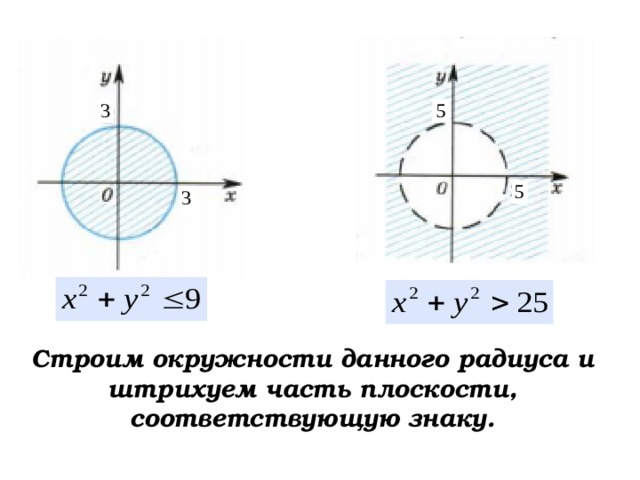
Строим окружности данного радиуса и штрихуем часть плоскости, соответствующую знаку.
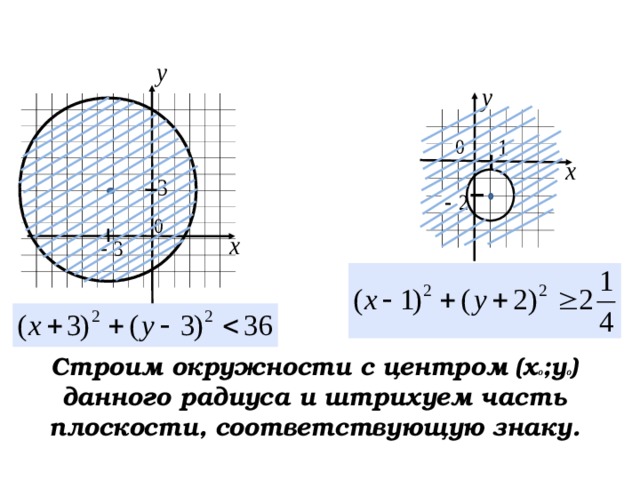
Строим окружности с центром (х 0 ;у 0 ) данного радиуса и штрихуем часть плоскости, соответствующую знаку.
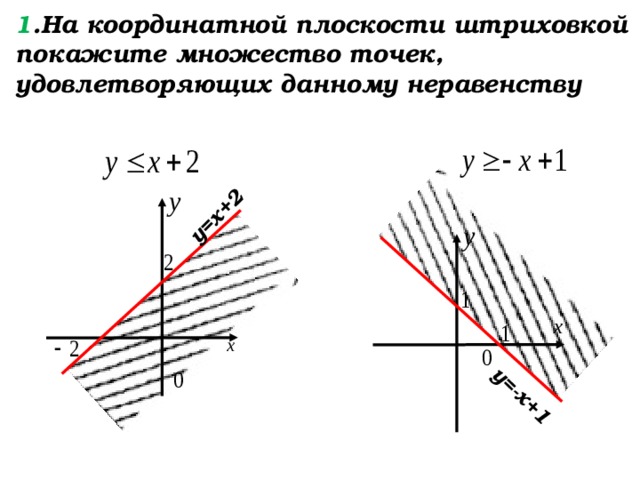
1 .На координатной плоскости штриховкой покажите множество точек, удовлетворяющих данному неравенству
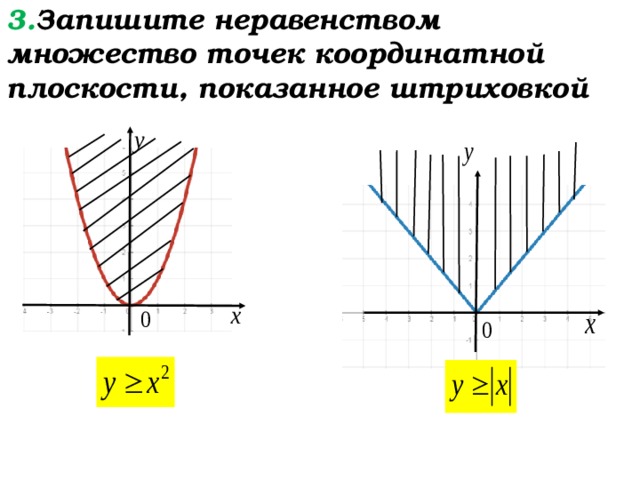
3. Запишите неравенством множество точек координатной плоскости, показанное штриховкой
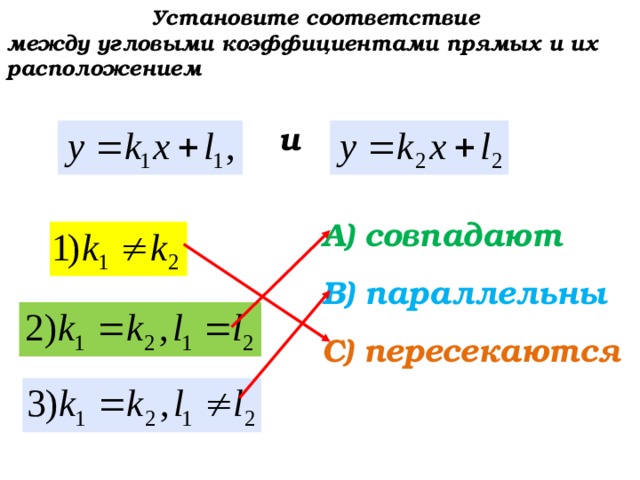
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
между угловыми коэффициентами прямых и их расположением
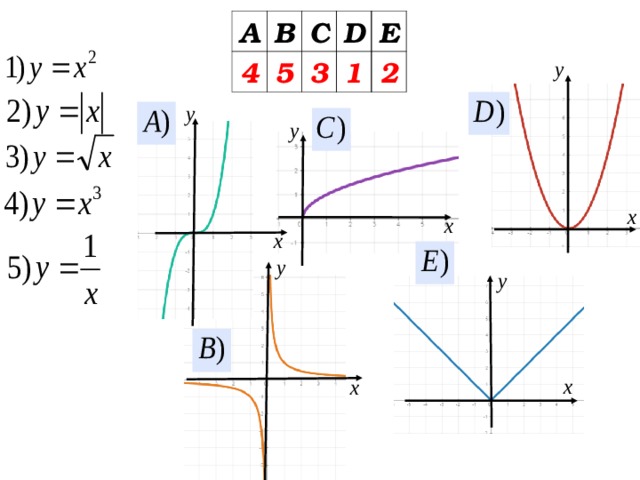
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Укажите название линии графика функции из правого столбца, по её формуле, записанной в левом столбце
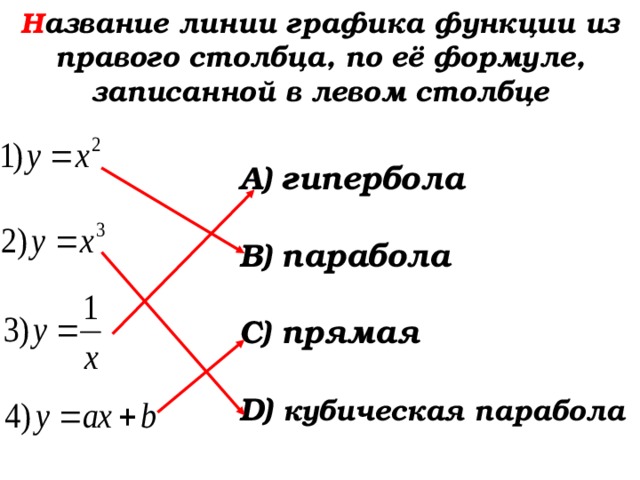
Н азвание линии графика функции из правого столбца, по её формуле, записанной в левом столбце
Назовите фигуру на координатной плоскости, заданную условием:
Назовите фигуру на координатной плоскости, заданную условием:
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Две параллельные прямые
Назовите фигуру на координатной плоскости, заданную условием:
Окружность с центром в точке (4;-1) и радиусом
Две параллельные прямые
Две параллельные прямые
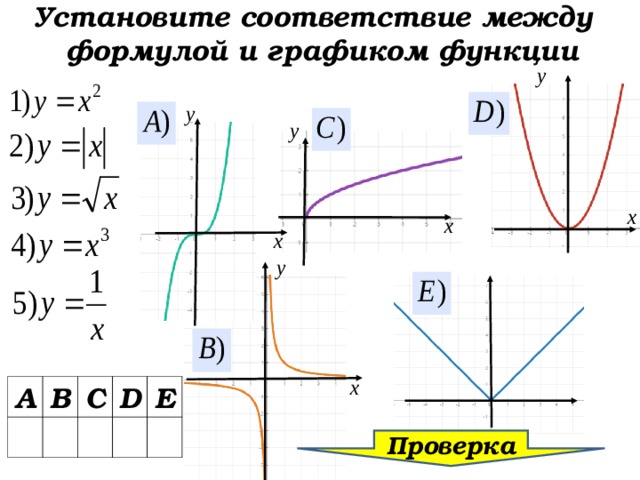
Установите соответствие между формулой и графиком функции
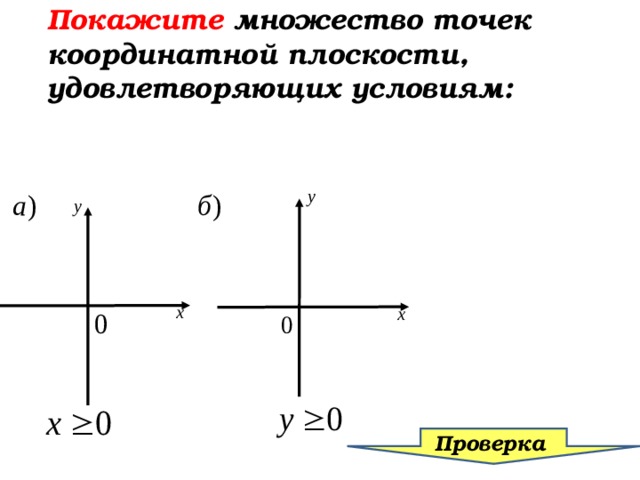
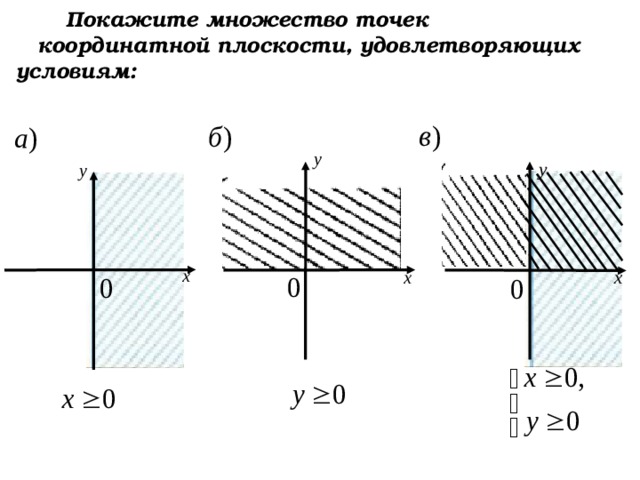
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
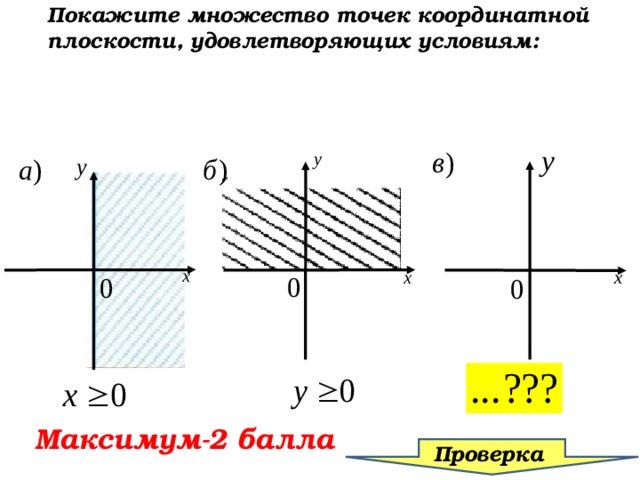
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
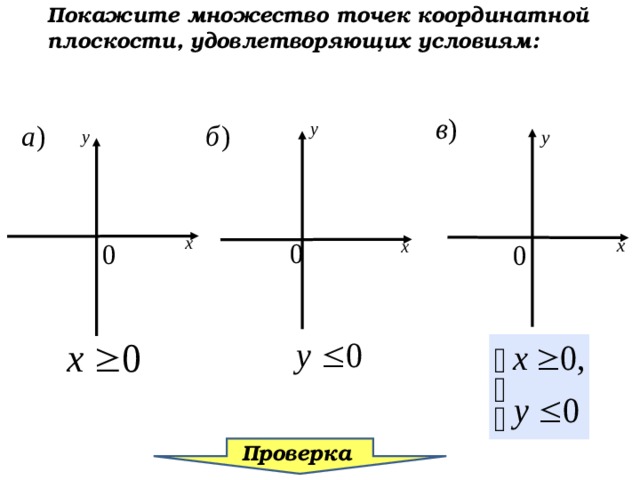
Покажите множество точек
координатной плоскости, удовлетворяющих условиям:
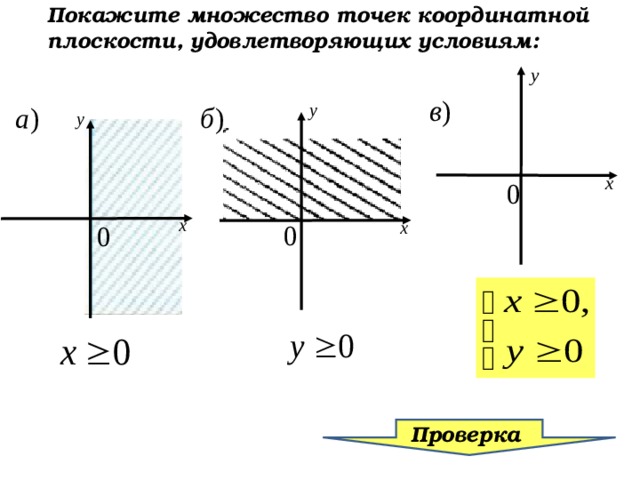
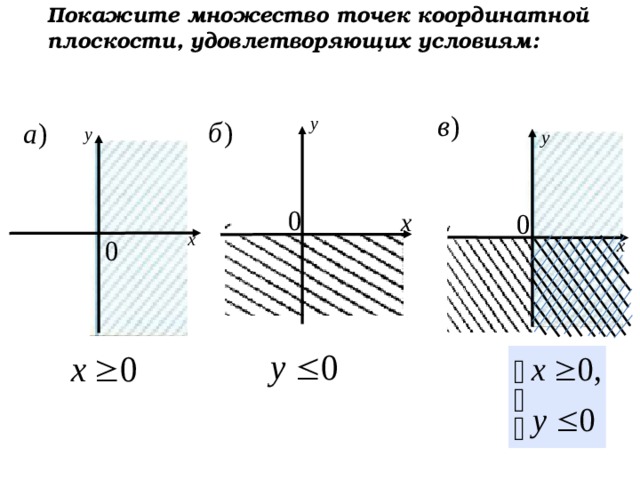
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
Покажите множество точек координатной плоскости, удовлетворяющих условиям:
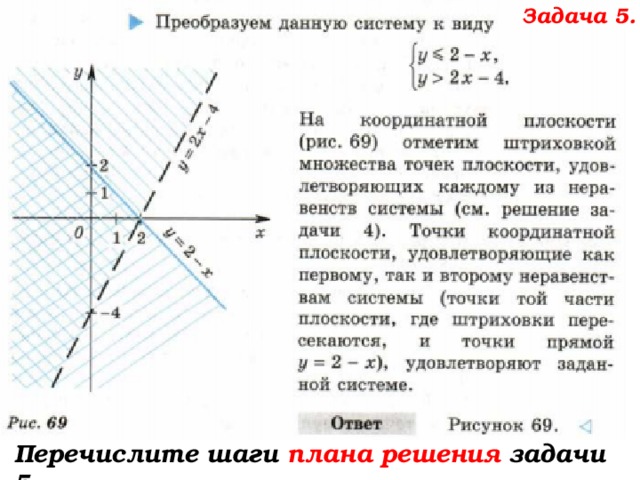
Задача. На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
На координатной плоскости изобразить множество точек, удовлетворяющих системе неравенств
Делаем выводы по решению.
Учимся решать подобные задачи.
Какое преобразование нужно выполнить в первом неравенстве?
Каков следующий шаг решения?
Выпуклые множества точек



Определение 1. Множество точек плоскости или трехмерного пространства называется выпуклым, если любые две точки этого множества можно соединить отрезком прямой, полностью лежащим в данном множестве (см. рис.6).
Рисунок 6 – Изображение множеств
Теорема 1. Пересечение конечного числа выпуклых множеств является выпуклым множеством.
Определение 2. Точка множества называется внутренней, если существует сколь угодно малая ее окрестность, содержащая только точки данного множества.
Определение 3. Точка множества называется граничной, если любая ее окрестность содержит как точки, принадлежащие данному множеству, так и не принадлежащие ему (см. рис. 7).
Определение 4. Граничная точка выпуклого множества называется угловой, если через нее можно провести отрезок, все точки которого не принадлежат данному множеству (см. рис. 7).
Различные по форме множества могут иметь конечное или бесконечное количество угловых точек.
Рисунок 7 – Изображение точек множества
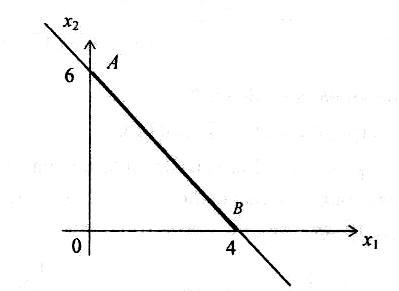
Пример 1. Определить угловые точки множества, заданного условиями 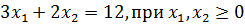
Решение. Уравнение 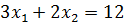
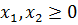
Множество точек отрезка АВ представляет собой выпуклое множество допустимых решений с двумя угловыми точками А(0;6)и В(4;0).
Рисунок 8 – решение примера 1
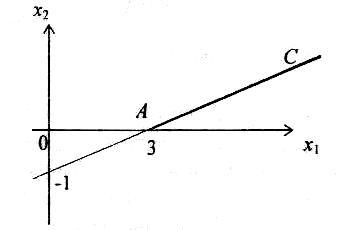
Пример 2. Определить угловые точки множества: 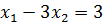
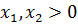
Решение. Множество допустимых решений – луч АС.
Здесь лишь одна угловая точка A (3,0) соответствует единственному допустимому базисному решению (см. рис. 9).
Рисунок 9 – решение примера 2
Как правило, система ограничений в задачах математического программирования представлена в виде системы неравенств, решение каждого из которых занимает определенную часть плоскости (пространства).
Теорема 2. Решением неравенства 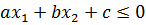
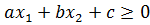
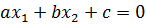
Пример 3. Построить множество точек, удовлетворяющих неравенству
Решение. Строим прямую 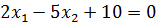
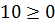
Рисунок 10 – решение примера 3
Пример 4. Построить множество точек, удовлетворяющих неравенству 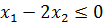
Решение. Строим прямую 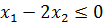
Рисунок 11 – решение примера 4
Прямая разделила всю плоскость на две полуплоскости, одна из которых и является решением неравенства. Для проверки выберем, например, точку А (4; 1) и ее координаты подставим в исходное неравенство. Получим ложное неравенство 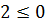
Замечание. Для того чтобы найти множество точек, удовлетворяющих системе линейных неравенств, необходимо решить каждое из неравенств и затем найти пересечение этих решений.
Пример 5. Построить множество точек, удовлетворяющих системе неравенств:
Рисунок 12 – решение примера 5
Задачи для самостоятельного решения
1. Какие из множеств, изображенных на рис. 13, являются выпуклыми?
Рисунок 13 – Изображение множеств
2. Проверить, будут ли выпуклыми данные множества:
б) круг
в) сфера 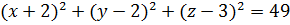
г) отрезок и точка, лежащая вне этого отрезка на плоскости;
д) два отрезка, имеющие одну общую точку;
е) два треугольника, имеющие одну общую точку/
3. Выяснить, будут ли выпуклы данные множества. Найти угловые точки данных множеств:
а)
б)
в)
5. Найти вершины многогранных множеств, ограничения для которых приведены в условиях:
а)
б)
в)
г)