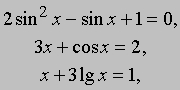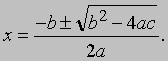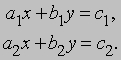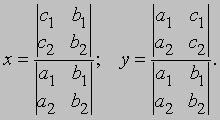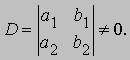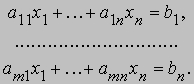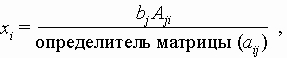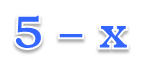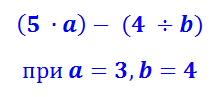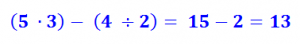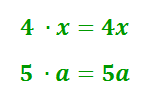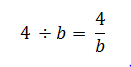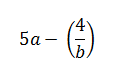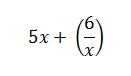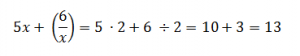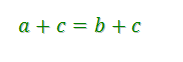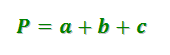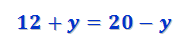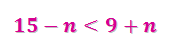Как называется математическое равенство содержащее переменную
Словари
1. процесс действия по гл. уравнивать I, уравниваться I 1.
2. Результат такого действия; уравнивание I 2..
Математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определённых значениях этих величин.
УРАВНЕ́НИЕ, уравнения, ср.
2. Математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определенных значениях этих неизвестных величин (мат.). Уравнение с одним неизвестным, с двумя неизвестными. Квадратное уравнение.
2. Математическое равенство с одной или несколькими неизвестными величинами (числами или функциями), верное только для определённых наборов этих величин. Квадратное у. Дифференциальное у.
3. химическое уравнение запись реакции с помощью формул и численных коэффициентов.
1. к Уравня́ть и Уравня́ться. У. опор. У. окладов. У. прав.
2. Математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определённых значениях этих неизвестных величин. Алгебраическое, дифференциальное у. У. с одним неизвестным.
◊ Уравне́ние времени. Астрон. Разность между средним и истинным солнечным временем, с помощью которой можно найти среднее местное время.
1. Действие по знач. глаг. уравнять и состояние по знач. глаг. уравняться.
Печать уравнения лежала на всех лицах, и часто Никита Иваныч здоровался с Карпом Спиридонычем, разумея при этом Павла Иваныча, и наоборот. Серафимович, Преступление.
2. Математическое равенство, содержащее одну или несколько неизвестных величин и сохраняющее свою силу только при определенных значениях этих неизвестных величин.
Алгебраическое уравнение. Дифференциальное уравнение. Уравнение с одним неизвестным.
разность между средним и истинным солнечным временем, с помощью которой можно найти среднее местное время.
= сущ. справедливость. Господие, правду и уравнение рабом подавайте, ведяще яко и вы имате Господа на небесех (Колос. 4, 1).
уравне́ние, уравне́ния, уравне́ний, уравне́нию, уравне́ниям, уравне́нием, уравне́ниями, уравне́нии, уравне́ниях
сущ., кол-во синонимов: 5
Ant: расслоение, размежевание
равенство, содержащее неизвестные (переменные) и справедливое лишь
при некоторых значениях (решениях) неизвестных (вывести #. решать #).
квадратное уравнение. биквадратное уравнение.
уравнения математической физики.
описываться уравнением => субъект, вербализация
решать дифференциальные уравнения => решение
— Задачка по выведению икса на чистую воду.
— Равенство с одной или несколькими неизвестными величинами.
— Пьеса Марии Арбатовой «. с двумя известными».
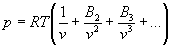
1) термическое уравнение состояния выражает связь между давлением p, температурой Т и удельным объемом v (или плотностью r) гомогенного вещества в состоянии равновесия: f(p,T,v)=0.
описываться уравнением => субъект, вербализация
Трансцендентные уравнения. Уравнения, содержащие трансцендентные функции, такие, как логарифмическая, показательная или тригонометрическая функция, называются трансцендентными. Примером могут служить следующие уравнения:
Дифференциальные уравнения. Так называются уравнения, содержащие одну или несколько функций и их производные или дифференциалы. Дифференциальные уравнения оказались исключительно ценным средством точной формулировки законов природы.
Интегральные уравнения. Уравнения, содержащие неизвестную функцию под знаком интеграла, например, f (s) = тK (s, t) f (t) dt, где f (s) и K(s,t) заданы, а f (t) требуется найти.
РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ
Для всех перечисленных выше типов уравнений общих методов решения не существует. И все же во многих случаях, особенно для алгебраических уравнений определенного типа, имеется достаточно полная теория их решения.
Линейные уравнения. Эти простые уравнения решаются путем их сведения к эквивалентному уравнению, из которого непосредственно видно значение неизвестного. Например, уравнение x + 2 = 7 можно свести к эквивалентному уравнению x = 5 вычитанием числа 2 из правой и левой частей. Шаги, совершаемые при сведении простого уравнения, например, x + 2 = 7, к эквивалентному, основаны на использовании четырех аксиом. 1. Если равные величины увеличить на одно и то же число, то результаты будут равны. 2. Если из равных величин вычесть одно и то же число, то результаты будут равны. 3. Если равные величины умножить на одно и то же число, то результаты будут равны. 4. Если равные величины разделить на одно и то же число, то результаты будут равны. Например, чтобы решить уравнение 2x + 5 = 15, мы воспользуемся аксиомой 2 и вычтем число 5 из правой и левой частей, в результате чего получим эквивалентное уравнение 2x = 10. Затем мы воспользуемся аксиомой 4 и разделим обе части полученного уравнения на 2, в результате чего исходное уравнение сведется к виду x = 5, что и является искомым решением.
Квадратные уравнения. Решения общего квадратного уравнения ax2 + bx + c = 0 можно получить с помощью формулы
Таким образом, существуют два решения, которые в частном случае могут совпадать.
, т.е. всего 3 корня. Если уравнение не факторизуется, то следует воспользоваться приближенными решениями. Основные методы нахождения приближенных решений были разработаны Горнером, Ньютоном и Греффе. Однако во всех случаях существует твердая уверенность в том, что решение существует: алгебраическое уравнение n-й степени имеет ровно n корней.
Системы линейных уравнений. Два линейных уравнения с двумя неизвестными можно записать в виде
Решение такой системы находится с помощью определителей
Оно имеет смысл, если
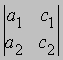
Если же D = 0, то возможны два случая. (1) По крайней мере один из определителей
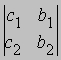
отличен от нуля. В этом случае решения уравнений не существует;
(2) Оба определителя равны нулю. В этом случае второе уравнение просто кратно первому и существует бесконечное
число решений. Общая теория рассматривает m линейных уравнений с n переменными:
Если m = n и матрица (aij) невырожденна, то решение единственно и может быть найдено по правилу Крамера:
УРА́ВНЕННЫЙ, уравненная, уравненное; уравнен, уравнена, уравнено, и УРАВНЁННЫЙ, уравнённая, уравнённое; уравнён, уравнена, уравнено. прич. страд. прош. вр. от уравнять.
ура́вненный и устаревающее уравнённый.
Выражения с переменными. Буквенные равенства и неравенства
Выражениями с переменными называются выражения содержащие переменные.
В задачах и примерах буквенные выражения используются для вычисления выражений с заданными переменными. То есть вместо букв надо подставить заданные значения:
Подставляем в выражение значения вместо букв:
Произведения с переменными записывают без знака умножения (·):
Если в выражениях участвует деление, такие выражения записывают в виде дроби:
Соответственно выражение в предыдущем примере можно записать следующим образом:
Давайте рассмотрим ещё один пример:
при x = 2
Если в выражении встречается несколько раз одна и та же буква (переменная), то ей соответствует одно и то же значение.
В таком случае решение будет следующим:
Буквенные равенства
Буквенными равенствами или равенствами с переменными называют выражения, которые содержат буквы (переменные).
В предыдущей статье мы рассматривали свойства числовых равенств и приводили выражение:
Это и есть пример буквенного равенства.
Буквенные равенства применяют, например, для записи различных физических или математических формул:
Например, вычисление периметра треугольника:
При подстановке численных значений переменных получаются верные или неверные числовые равенства.
Буквенные равенства обладают теми же свойствами, что и числовые.
Буквенные неравенства
Буквенными неравенствами называют неравенства с переменными.
интернет проект BeginnerSchool.ru
Сайт для детей и их родителей
Выражения с переменными. Буквенные равенства и неравенства.
Выражения с переменными
Выражениями с переменными называются выражения содержащие переменные.
В задачах и примерах буквенные выражения используются для вычисления выражений с заданными переменными. То есть вместо букв надо подставить заданные значения:
Подставляем в выражение значения вместо букв:
Произведения с переменными записывают без знака умножения (·):
Если в выражениях участвует деление, такие выражения записывают в виде дроби:
Соответственно выражение в предыдущем примере можно записать следующим образом:
Давайте рассмотрим ещё один пример:
при x = 2
Если в выражении встречается несколько раз одна и та же буква (переменная), то ей соответствует одно и то же значение.
В таком случае решение будет следующим:
Буквенные равенства
Буквенными равенствами или равенствами с переменными называют выражения, которые содержат буквы (переменные).
В предыдущей статье мы рассматривали свойства числовых равенств и приводили выражение:
Это и есть пример буквенного равенства.
Буквенные равенства применяют, например, для записи различных физических или математических формул:
Например, вычисление периметра треугольника:
При подстановке численных значений переменных получаются верные или неверные числовые равенства.
Буквенные равенства обладают теми же свойствами, что и числовые.
Буквенные неравенства
Буквенными неравенствами называют неравенства с переменными.
Спасибо, что Вы с нами!
Оставляйте пожалуйста комментарии в форме ниже
А) Дополните предложения так, чтобы получились верные определения :Равенство, содержащее переменную, называется __________________?
А) Дополните предложения так, чтобы получились верные определения :
Равенство, содержащее переменную, называется __________________.
Значение переменной, при котором________________обращается в верное_______________, называется___________________,
Б)Линейным уравнение с одной переменной называеися уравнение вида____, где _________________.
выражение, равенство, корнем уравнения
При каких значениях переменной верно равенство : =?
При каких значениях переменной верно равенство : =.
Равенство верное при всех допустимых значениях входящих в него переменных называется?
Равенство верное при всех допустимых значениях входящих в него переменных называется.
Какие из равенств являются верными для большинства значений переменных?
Какие из равенств являются верными для большинства значений переменных?
1. при каких значениях переменных верно равенство?
1. при каких значениях переменных верно равенство.
Что называют частным решением неравенства с одной переменной?
Что называют частным решением неравенства с одной переменной?
Что называют общим решением неравенства с одной переменной?
При каком значении переменной Y верно равенство под корнем Y равно 7 деленное на 2 помогите пожалуйста?
При каком значении переменной Y верно равенство под корнем Y равно 7 деленное на 2 помогите пожалуйста.
Что называется линейным уравнением с двумя переменными и его график?
Что называется линейным уравнением с двумя переменными и его график!
Продолжите задания по теоритическому материалу 1?
Продолжите задания по теоритическому материалу 1.
Равенство верное при любых значениях переменных называется.
3. Чтобы поделить степени с одинаковыми основаниями.
4. Степени одночлена называют.
5. Одночлен стандартного вида содержит.
Функцией называется зависимость одной переменной от другой?
Функцией называется зависимость одной переменной от другой.
При каком значении переменной y верно равенство :
СОДЕРЖАНИЕ
Этимология
Этимологию этого слова от латинского aequālis ( «равно», «как», «сопоставимы», «подобные») от aequus ( «равный», «уровень», «ярмарка», «просто»).
Основные свойства
Вот некоторые конкретные примеры этого:
Равенство как предикат
Идентичности
Уравнения
Не существует стандартной нотации, которая отличает уравнение от тождества или другого использования отношения равенства: нужно угадывать подходящую интерпретацию из семантики выражений и контекста. Утверждается, что идентичность истинна для всех значений переменных в данной области. «Уравнение» иногда может означать идентичность, но чаще всего оно определяет подмножество пространства переменных как подмножество, в котором уравнение истинно.
Сравнения
Примерное равенство
Проверяемое сомнительное равенство можно обозначить символом.
Связь с эквивалентностью и изоморфизмом
Однако есть и другие варианты изоморфизма, например
Логические определения
Лейбниц охарактеризовал понятие равенства следующим образом:
Равенство в теории множеств
Равенство множеств аксиоматизируется в теории множеств двумя разными способами, в зависимости от того, основаны ли аксиомы на языке первого порядка с равенством или без него.
Установите равенство на основе логики первого порядка с помощью равенства
В логике первого порядка с равенством аксиома протяженности утверждает, что два набора, содержащие одинаковые элементы, являются одним и тем же набором.
Включение половины работы в логику первого порядка можно рассматривать как простое удобство, как отмечает Леви.
«Причина, по которой мы беремся за исчисление предикатов первого порядка с равенством, заключается в удобстве; тем самым мы экономим труд по определению равенства и доказательству всех его свойств; теперь это бремя ложится на логику».