Как называется двадцатигранник в геометрии
Икосаэдр
Математические характеристики икосаэдра
Икосаэдр может быть помещен в сферу (вписан), так, что каждая из его вершин будет касаться внутренней стенки сферы.
Радиус описанной сферы икосаэдра
Сфера может быть вписана внутрь икосаэдра.
Радиус вписанной сферы икосаэдра
Для наглядности площадь поверхности икосаэдра можно представить в виде площади развёртки.
Площадь поверхности можно определить как площадь одной из сторон икосаэдра (это площадь правильного треугольника) умноженной на 20. Либо воспользоваться формулой:
Объем икосаэдра определяется по следующей формуле:
Вариант развертки
Древнегреческий философ Платон ассоциировал икосаэдр с «земным» элементом вода, поэтому для построения модели этого правильного многогранника мы выбрали голубой цвет.
Заметим, что это не единственный вариант развертки.
Кроме того, существуют два классических варианта окраски многогранника, когда каждая из соседних граней окрашена в свой цвет. Либо используется определенное количество цветов раскраски, причем одинаковые цвета не граничат друг с другом.
Представляем Вашему вниманию два варианта окраски 20 граней икосаэдра с использованием пяти цветов.
Икосаэдр — понятие, свойства и структура двадцатигранника
В геометрии, икосаэдр — одно из пяти платоновых тел. Представляет собой выпуклый правильный многогранник, состоящий из 20 треугольных граней, по пять на каждую из двенадцати вершин, и 30 рёбер. Существует много видов этого двадцатигранника, имеющих незначительные отличия.
Бумажная модель
Используя 30 квадратных листов бумаги (размер каждой стороны 7,5 см), можно сделать довольно крепкую версию одной из разновидности этого геометрического чуда совсем без склеивания. Если в запасе есть материал разного цвета, то получится яркий и красивый макет с разноцветными блоками. Инструкция по изготовлению звездчатого икосаэдра поэтапно:
Всего таких блоков нужно сделать 30. Например, по 10 разного цвета.
Сборка элементов
Теперь самое время собирать блоки вместе. Поверхность звездчатого икосаэдра состоит из нескольких пирамид. Чтобы было проще, нужно представить этот сложный куб, над которым идёт работа, в виде единственного додекаэдра (12-гранный правильный пятиугольник — ещё одно тело Платона), где каждая из его двадцати вершин будет заменена пирамидой. Все 30 единиц пойдут на формирование этих 20 пирамид. Ход работы по сборке икосаэдра. Схема поэтапно:
В итоге получится красивая объёмная фигура, а если она сделана из цветной бумаги, то ещё и красочная. Безусловно, если нужно сэкономить время и силы, можно сильно упростить задачу и найти готовый шаблон модели, распечатать развёртку икосаэдра на бумаге и вырезать, оставляя припуски, а затем склеить.
Основные виды
Вообще, эта геометрическая фигура — одно из платоновых тел, известных с древних времён. Их всего пять: тетраэдр, куб, октаэдр, додекаэдр и икосаэдр. Их определение довольно простое: все они представляют собой многогранники, состоящие из конгруэнтных (одинаковых по форме и размеру) регулярных (все углы равны, как и все стороны) полигональных граней, встречающихся в каждой вершине.
Обычный икосаэдр представлен в двух основных видах, обладающих одинаковыми признаками. У каждого есть 30 рёбер и 20 равносторонних треугольных граней, которые собираются по 5 штук, образуя 12 вершин. Оба имеют икосаэдрическую симметрию, центром которой является точка пересечения всех осевых линий, и называются:
Звездчатые формы образуются, когда грани или края многогранника расширяют до тех пор, пока они не встретятся, чтобы сформировать новую фигуру. Это делается таким образом, что сохраняются центр,оси и плоскости симметрии родительской фигуры. К слову, большой икосаэдр можно отнести к этому виду. У других «звёздочек» есть более одной грани в каждой плоскости или они образуют соединения более простых многогранников. Это не строго икосаэдры, но их часто так называют. В таблице представлены несколько разновидностей звездчатых тел.
| Вид икосаэдра | Рисунок |
| выпуклый | |
| малый триамбический | |
| медиальный (большой) триамбический | |
| соединение пяти октаэдров | |
| соединение из пяти тетраэдров | |
| финальный |
Ромбический икосаэдр — выпуклый многогранник, состоящий из двадцати конгруэнтных ромбических граней, четыре или пять из которых встречаются в каждой вершине. Напоминает сплюснутую сферу.
По специальным формулам икосаэдра определяют его размер, площадь и объём. А также есть специальные координаты — декартовы и сферические, с помощью которых описывают расположение вершин многогранника. Построение такой фигуры, чтобы избежать утомительных расчётов, можно проводить с помощью квадратных матриц по системе равносторонних линий. Другие интересные факты:
Икосаэдр имеет три специальных ортогональных проекции, центрированных на грани, ребре и вершине. Фигура также может быть представлена в виде сферической мозаики и спроецирована на плоскость через стереографическую проекцию.
Природные формы и использование
Многие микроорганизмы, в том числе вирусы, имеют икосаэдрические оболочки. Их структуры построены из повторяющихся идентичных белковых субъединиц, и икосаэдр является самой лёгкой формой для их сборки. Используется обычный тип многогранника, поскольку он может быть построен из одного базового белка, который будет использоваться снова и снова. Это очень упрощает жизнь и экономит место в вирусном геноме.
А также были обнаружены различные органеллы бактериальной клетки с икосаэдрической формой. В 1904 году Эрнст Геккель описал ряд видов радиолярий, чей скелет имеет форму и свойства многогранника. Икосаэдрическое двойникование также происходит в кристаллах, особенно в наночастицах.
К другим примерам того, как природа использует такую структуру для достижения многих целей, можно отнести инклюзионные тела — компартменты, которые образуются внутри клеток, обычно во время некоторых фаз роста или в определённых условиях окружающей среды.
Использование икосаэдров для разделения пространства и контроля доступа очень эффективно и, по-видимому, предпочтительно, когда ресурсы организмов ограничены.
В древности игральные кости имели столько сторон, сколько граней в икосаэдре. Такие двадцатигранные кубики могли быть пронумерованы от 0 до 9 дважды или от 1 до 20. Форма правильных многогранников часто используется для создания различных предметов в компьютерных играх и головоломках. В виртуальном мире, кстати, часто можно встретить и другие геометрические тела. Например, в «Супер Марио Галактике» планеты имеют форму, похожую на ромбоусечённый икосододекаэдр — архимедово тело.
Японский картограф Содзи Садао и американский архитектор Ричард Бакминстер Фуллер разработали карту мира в виде развёрнутого икосаэдра. Этот же многогранник лежит в основе геодезических сеток, которыми пользуются метеорологи и климатологи.
Икосаэдр
| Икосаэдр | |
|---|---|
 анимация анимация |
|
| Тип | Правильный многогранник |
| Грань | Правильный треугольник |
| Граней | 20 |
| Рёбер | 30 |
| Вершин | 12 |
| Граней при вершине | 5 |
| Площадь |  |
| Объем |  |
| Радиус вписанной сферы |  |
| Радиус описанной сферы |  |
| Группа симметрии | Икосаэдрическая (Ih) |
| Двойственный многогранник | додекаэдр |
Икоса́эдр (от др.-греч. εἴκοσι «двадцать»; ἕδρον «сидение», «основание») — правильный выпуклый многогранник, двадцатигранник, одно из Платоновых тел. Каждая из 20 граней представляет собой равносторонний треугольник. Число ребер равно 30, число вершин — 12. Икосаэдр имеет 59 звёздчатых форм.
Площадь S, объём V икосаэдра с длиной ребра a, а также радиусы вписанной и описанной сфер вычисляются по формулам:
площадь:
объём:
радиус вписанной сферы:
радиус описанной сферы:
Содержание
Свойства
Усечённый икосаэдр
Усечённый икосаэдр — многогранник, состоящий из 12 правильных пятиугольников и 20 правильных шестиугольников. Имеет икосаэдрический тип симметрии.





























 Многогранники
Многогранники 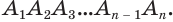
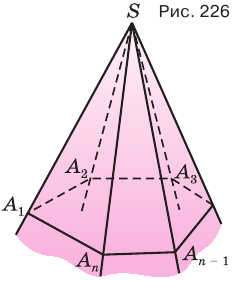
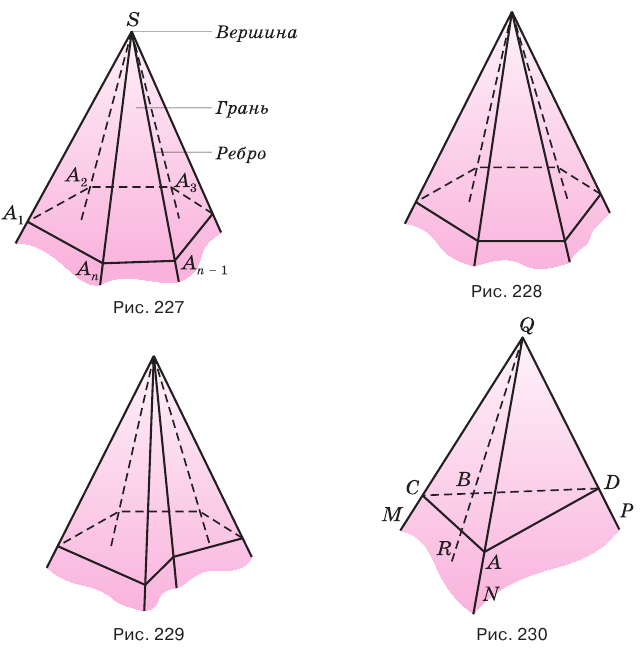
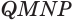 (рис. 230). Пусть для определенности угол
(рис. 230). Пусть для определенности угол 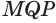 — больший из плоских углов трехгранного угла. В плоскости грани
— больший из плоских углов трехгранного угла. В плоскости грани 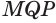 от луча
от луча 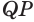 отложим угол
отложим угол 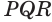 , равный углу
, равный углу 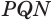 , и на лучах
, и на лучах 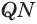 и
и 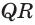 отложим равные отрезки
отложим равные отрезки 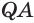 и
и 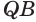 . Через прямую
. Через прямую 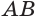 проведем такую плоскость, которая пересекает ребра
проведем такую плоскость, которая пересекает ребра 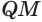 и
и 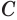 и
и 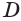 . Треугольники
. Треугольники 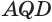 и
и 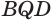 равны, так как у них сторона
равны, так как у них сторона 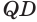 общая, и по построению равны углы
общая, и по построению равны углы 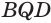 и
и 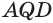 , а также стороны
, а также стороны 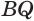 и
и 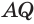 . Значит,
. Значит, 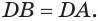 Далее по свойству сторон треугольника получаем
Далее по свойству сторон треугольника получаем 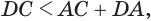 или
или 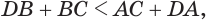 или
или 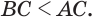 Теперь, поскольку у треугольников
Теперь, поскольку у треугольников 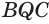 и
и 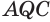 сторона
сторона 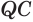 общая, стороны
общая, стороны 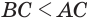 , то
, то 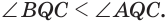 Прибавив к левой и правой частям этого неравенства соответственно углы
Прибавив к левой и правой частям этого неравенства соответственно углы 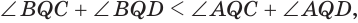 или
или 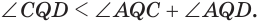
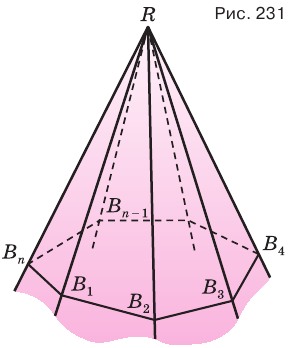
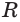 (рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник
(рис. 231). Если пересечь его какой-либо плоскостью, то в сечении получим многоугольник 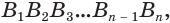 каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем:
каждая вершина которого является вершиной трехгранного угла, образованного двумя гранями данного угла и секущей плоскостью. По доказанному для этих трехгранных углов получаем: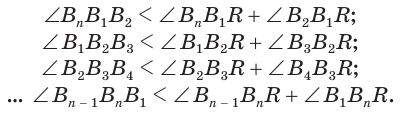
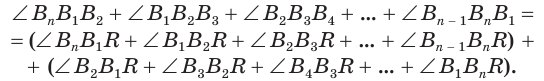
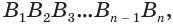 которая равна
которая равна 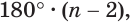 а в правой — сумма углов всех треугольников
а в правой — сумма углов всех треугольников 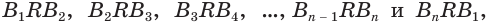 но без их углов при вершине
но без их углов при вершине 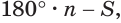 где
где 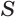 выражает сумму плоских углов данного многогранного угла. Таким образом,
выражает сумму плоских углов данного многогранного угла. Таким образом,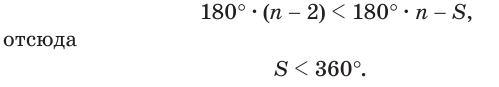
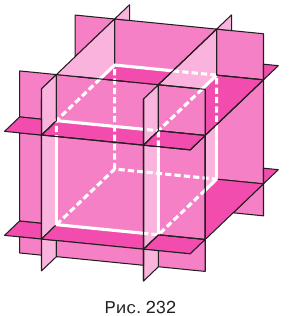
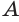 и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине
и в каждой грани с этой вершиной выбрать вершину, противолежащую вершине 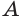 . Пусть это вершины
. Пусть это вершины 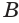 ,
, 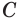 ,
, 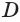 . Точки
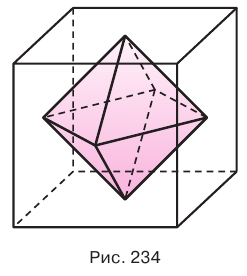
. Точки 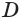 являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков
являются вершинами искомого многогранника (рис. 233). Действительно, каждый из отрезков 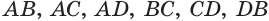 является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде
является диагональю одной из граней куба, а поэтому все эти отрезки равны друг другу. Получается, что в треугольной пирамиде 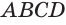 все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.
все грани являются правильными треугольниками. Такая пирамида называется правильным тетраэдром. Тетраэдр имеет 4 грани, 6 ребер и 4 вершины.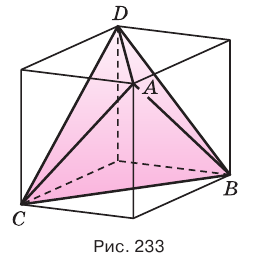
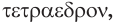 означает четырехгранник:
означает четырехгранник: 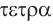 — четыре и
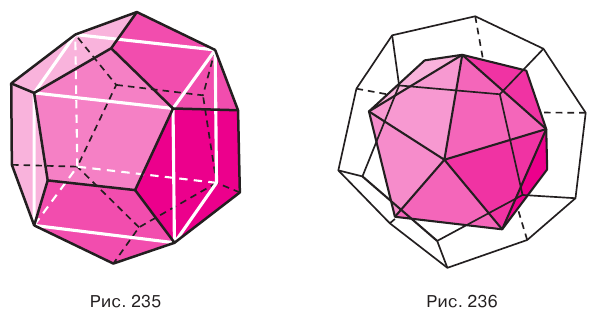
— четыре и 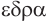 — грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески
— грань. Соответственно термины гексаэдр, октаэдр, додекаэдр, икосаэдр, по-гречески 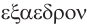 ,
, 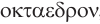 ,
, 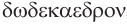 ,
, 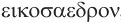 , означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник:
, означают шестигранник, восьмигранник, двенадцатигранник, двадцатигранник: 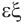 , — шесть,
, — шесть, 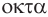 — восемь,
— восемь, 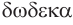 — двенадцать,
— двенадцать, 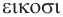 — двадцать.
— двадцать.