Как называется цифра снизу числа
Степень числа: определения, обозначение, примеры
В рамках этого материала мы разберем, что такое степень числа. Помимо основных определений мы сформулируем, что такое степени с натуральными, целыми, рациональными и иррациональными показателями. Как всегда, все понятия будут проиллюстрированы примерами задач.
Степени с натуральными показателями: понятие квадрата и куба числа
Сначала сформулируем базовое определение степени с натуральным показателем. Для этого нам понадобится вспомнить основные правила умножения. Заранее уточним, что в качестве основания будем пока брать действительное число (обозначим его буквой a ), а в качестве показателя – натуральное (обозначим буквой n ).
Разберем пример степени с натуральным показателем: для 5 7 пятерка будет основанием, а семерка – показателем.
Понятие степени является обратным другому математическому понятию – корню числа. Если мы знаем значение степени и показатель, мы можем вычислить ее основание. Степень обладает некоторыми специфическими свойствами, полезными для решения задач, которые мы разобрали в рамках отдельного материала.
Что такое степени с целым показателем
В показателях степени могут стоять не только натуральные числа, но и вообще любые целые значения, в том числе отрицательные и нули, ведь они тоже принадлежат к множеству целых чисел.
Степень числа с целым положительным показателем можно отобразить в виде формулы: 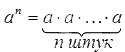
При этом n – любое целое положительное число.
Разберемся с понятием нулевой степени. Для этого мы используем подход, учитывающий свойство частного для степеней с равными основаниями. Оно формулируется так:
Последнее условие важно, поскольку позволяет избежать деления на ноль. Если значения m и n равны, то мы получим следующий результат: a n : a n = a n − n = a 0
При желании легко проверить, что a 0 = 1 сходится со свойством степени ( a m ) n = a m · n при условии, что основание степени не равно нулю. Таким образом, степень любого отличного от нуля числа с нулевым показателем равна единице.
Такая формулировка подтверждает, что для степени с целым отрицательным показателем действительны все те же свойства, которыми обладает степень с натуральным показателем (при условии, что основание не равно нулю).
Проиллюстрируем нашу мысль конкретными примерами:
В последней части параграфа попробуем изобразить все сказанное наглядно в одной формуле:
Что такое степени с рациональным показателем
Мы разобрали случаи, когда в показателе степени стоит целое число. Однако возвести число в степень можно и тогда, когда в ее показателе стоит дробное число. Это называется степенью с рациональным показателем. В этом пункте мы докажем, что она обладает теми же свойствами, что и другие степени.
Далее нам необходимо определить, какие именно ограничения на значения переменных накладывает такое условие. Есть два подхода к решению этой проблемы.
Для степени с нулевым основанием это положение также подходит, но только в том случае, если ее показатель – положительное число.
Степень с нулевым основанием и дробным положительным показателем m / n можно выразить как
При отрицательном отношении m n 0 степень не определяется, т.е. такая запись смысла не имеет.
Отметим один момент. Поскольку мы ввели условие, что a больше или равно нулю, то у нас оказались отброшены некоторые случаи.
Если n – нечетное число, а значение m – положительно, a – любое неотрицательное число, то a m n имеет смысл. Условие неотрицательного a нужно, поскольку корень четной степени из отрицательного числа не извлекают. Если же значение m положительно, то a может быть и отрицательным, и нулевым, т.к. корень нечетной степени можно извлечь из любого действительного числа.
Объединим все данные выше определения в одной записи:
Здесь m/n означает несократимую дробь, m – любое целое число, а n – любое натуральное число.
Определение степени с дробным показателем, которое мы привели первым, удобнее применять на практике, чем второе, поэтому мы будем далее пользоваться именно им.
При вычислении же лучше заменять показатель степени обыкновенной дробью и далее пользоваться определением степени с дробным показателем. Для примеров выше у нас получится:
Что такое степени с иррациональным и действительным показателем
Что такое действительные числа? В их множество входят как рациональные, так и иррациональные числа. Поэтому для того, чтобы понять, что такое степень с действительным показателем, нам надо определить степени с рациональными и иррациональными показателями. Про рациональные мы уже упоминали выше. Разберемся с иррациональными показателями пошагово.
и так далее (при этом сами приближения являются рациональными числами).
Разряды и классы чисел
Числа и цифры
Числа — это единицы счета. С помощью чисел можно сосчитать количество предметов и определить различные величины.
Для записи чисел используются специальные знаки — цифры. Всего их десять: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Натуральные числа — это числа, которые мы используем при счете. Вот они: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, …
От количества цифр в числе зависит его название.
Число, которое состоит из одного знака, называется однозначным. Наименьшее однозначное — 1, наибольшее — 9.
Число, которое состоит из двух знаков цифр, называется двузначным. Наименьшее двузначное — 10, наибольшее — 99.
Числа, которые записаны с помощью двух, трех, четырех и более цифр, называются двузначными, трехзначными, четырехзначными или многозначными. Наименьшее трехзначное — 100, наибольшее — 999.
Каждая цифра в записи многозначного числа занимает определенное место — позицию.
Классы чисел
Цифры в записи многозначных чисел разбивают справа налево на группы по три цифры в каждой. Эти группы называют классами. В каждом классе цифры справа налево обозначают единицы, десятки и сотни этого класса.
Названия классов многозначных чисел справа налево:
Чтобы читать запись многозначного числа было удобно, между классами оставляют небольшой пробел. Например, чтобы прочитать число 125911723296, удобно сначала выделить в нем классы:
А теперь прочитаем число единиц каждого класса слева направо:
Разряды чисел
От позиции, на которой стоит цифра в записи числа, зависит ее значение. Например:
Можно сформулировать иначе и сказать, что в заданном числе 1 123 цифра 3 располагается в разряде единиц, 2 в разряде десятков, 1 в разряде сотен, а 1 служит значением разряда тысяч.
Проясним, что такое разряд в математике. Разряд — это позиция или место расположения цифры в записи натурального числа.
У каждого разряда есть свое название. Слева всегда живут старшие разряды, а справа — младшие. Чтобы быстрее запомнить, можно использовать таблицу.
Количество разрядов всегда соответствует количеству знаков в числе. В этой таблице есть названия всех разрядов для числа, которое состоит из 15 знаков. У следующих разрядов также есть названия, но они используются крайне редко.
Низший (младший) разряд многозначного натурального числа — разряд единиц.
Высший (старший) разряд многозначного натурального числа — разряд, соответствующий крайней левой цифре в заданном числе.
Разрядные единицы обозначают так:
Каждые три разряда, следующие друг за другом, составляют класс. Первые три разряда: единицы десятки и сотни — образуют класс единиц (первый класс). Следующие три разряда: единицы тысяч, десятки тысяч и сотни тысяч — образуют класс тысяч (второй класс). Третий класс будут составлять единицы, десятки и тысячи миллионов и так далее.
Чтобы легче понимать математику — записывайтесь на наши курсы по математике!
Потренируемся
Пример 1. Записать цифрами число, в котором содержится:
Все разрядные единицы, кроме простых единиц, называют составными единицами. Каждые десять единиц любого разряда составляют одну единицу следующего более высокого разряда:
Чтобы узнать, сколько в числе заключается всех единиц какого-либо разряда, нужно отбросить все цифры, обозначающие единицы низших разрядов и прочитать число, которое выражено оставшимися цифрами.
Пример 2. Сколько сотен содержится в числе 6284?
В числе 6284 на третьем месте в классе единиц стоит цифра 2, значит, в числе есть две сотни.
Следующая цифра слева — 6, означает тысячи. Так как в каждой тысяче содержится 10 сотен то, в 6 тысячах их заключается 60.
Значит, в данном числе содержится 62 сотни.
Цифра 0 в любом разряде означает отсутствие единиц в данном разряде.
Проще говоря, цифра 0 в разряде десятков означает отсутствие десятков, в разряде сотен — отсутствие сотен и т. д. В том разряде, где стоит 0, при чтении числа ничего не произносится:
Чтобы проще освоить эту тему, можно распечатать таблицу классов и разрядов для учащихся 4 класса и обращаться к ней, если возникнут сложности.
Как написать маленькие цифры снизу
Можно маленькие цифры и буквы поставить в ник, текст, ворд. Скопировать и вставить.
Арабские цифры и математические знаки
Буквы
На этой странице собраны подстрочные и надстрочные маленькие цифры и буквы. Если нужно поставить степень числа (666*10⁻¹⁹), написать размерность метры кубические (м³), уравнение (y=x²) или оформить сноску вам могут пригодиться эти символы. Также их можно использовать для придания оригинальности нику или сообщению в социальной сети, тогда, когда сервис не обладает широкими возможностями по форматированию текста. В word, конечно, всё проще, но не везде можно сделать также. Подстрочные цифры помогут химикам в написании формул (C₂H₅OH).
Этот текст также доступен на следующих языках: English;
Как сделать маленькую цифру снизу в ворде
Автор VB задал вопрос в разделе Прочее компьютерное
как в ворде сделать цифру внизу?например формулу пишешь, N-нулевое,чтоб нолик внизу был такой маленький.никак не найду и получил лучший ответ
Ответ от АПЕСиНКа)))[новичек]
Легко. если у тебя 2007 года верд то там надо нажать на кнопку x2. 2сверху.. этот значок находится на панели ШРИФТ)) ) удачи))
АПЕСиНКа))
Ученик
(206)
там тож такое должно быть..я давно 2003 не делала..поищи у тя уже есть оринтир)) 😉
Часто при написании различных параметров, например метр квадратный или кубический, необходимо написать число как степень. Если вам нужно сделать это один раз и навсегда забыть про степени, то вам достаточно всего-лишь скопировать число, записанное степенью, и вставить в нужное место: x² — квадрат, x³ — куб. Но если у вас есть постоянная необходимость записывать числа таким образом, то мы расскажем вам, как написать степень на клавиатуре, чтобы вы всегда могли сделать это сами.
Есть несколько способов, как написать число-степень на клавиатуре
Первый способ — удерживая клавишу Alt, набрать на цифровой клавиатуре клавиши в нужном порядке.

Второй способ — в редакторе Word
С помощью ворда можно ставить не только квадратную и кубическую степени, но и любые другие, в том числе буквенные. Например когда математические задачи требуют от степени числа быть переменной. Этот способ не связан с клавиатурой, больше с мышкой, но написать степень в Word очень просто. В верхнем меню есть специальный инструмент: надстрочный знак.
Выделяем число или буквы, которые нужно сделать степенью, и нажимаем на кнопку в верхнем меню, указанную на рисунке. Также можно воспользоваться сочетанием клавиш Ctrl+Shift+=. В результате можно получить любую степень, какая только нужна. Рядом есть инструмент «подстрочный знак», с помощью которого можно записывать число в нижнем регистре, например для логарифмов.
Третий способ — альтернативный для Word, работающий во всех версиях, в том числе старых
Нужно выделить текст, которой должен стать степенью, и нажать на него правой кнопкой. В появившемся меню нажать на вкладку «Шрифт».
В появившемся меню можно задать любые параметры выделенному тексту, в том числе и сделать его степенью. Для этого нужно поставить галочку в пункте «Надстрочный».
Вот и всё, теперь вы знаете, как написать степень на клавиатуре и можете применять этот навык в жизни.
О происхождении названий цифр
Материал подготовлен на основе выявленных автором первослов, из которых, как из атомов молекулы, сформировались слова праязыка. Эти первослова позволили понять изначальный смысл многих слов, а так же имен богов и героев древней мифологии и их суть. Стало возможным понимание смысла многих ритуалов и обрядов, а так же смысл и истоки мифов, легенд и религиозных воззрений.
При рассмотрении названий цифр я опираюсь на постулат, сформулированный мною, что первыми в человеческой речи появились слова, обозначающие названия половых органов человека. Названия других частей тела, а так же названия предметов и явлений окружающего мира появились позже на основе и в ассоциации со словами изначального сексуального словаря (см. в моем блоге «основные принципы словообразования в праязыке»)
Пять. Происхождение цифры пять восходит к копыту. Раздвоенное копыто тура ассоциировано было с вульвой (Пи). Изначально оно так и называлось: Пи то. Позже, когда так начали называть и пятку, для различения пятки и копыта к «Пи то» добавили первослово «це»-это. Получилось «це Пи то», которое переродилось в копыто. В русском языке женские половые органы так и называются словом Пи в сочетании с Да.
След копыта в виде углубления в земле ассоциирован с женским началом. Эти же ассоциации породили с слово пещера, и печь, называвшуюся в древнерусском языке словом пище (пещь). По этой причине братец Иванушка перерождается в козленочка, после того, как попил из следа от копытца. На Руси издревле существовал ритуал перепекания младенца в печи, в котором печь выполняла роль женской утробы.
Цифра два изначально произносилась, как то Ва (тва) – семя. В английском языке она так и пишется поныне (two). В немецком –цвай (це Ва). В греческом от «то Ва» осталась только «то», трансформировавшаяся в ди.
А вообще-то названия для счета один, раз, бир. Появились довольно поздно. У цифры один не было названия. Счет начинался с названия считаемого предмета: стул, два, три…, жена, две, три…, рюмка, другая, третья и т д.
Чтобы объяснить с чего и как появились названия цифр я начал с цифры пять. А пять имеет одни истоки со словом печь. Также начинали знакомить с азами древних знаний и волхвы своих волхвят. Чуете, откуда в русском языке выражение «танцевать от печки»?!
Собственно на этом счет и кончался и счет вели двойками (парами), четверками, шестерками, дюжинами.
Ноль (цифра)
Ноль (нуль, от лат. nullus — никакой) — название первой (по порядку) цифры в стандартных системах исчисления, а также математический знак, выражающий отсутствие значения данного разряда в записи числа в позиционной системе счисления. Цифра ноль, поставленная справа от другой цифры, увеличивает числовое значение всех левее стоящих цифр на разряд (например, в десятичной системе счисления, умножает на десять). Сравните, например, числа 410 и 4010; 416 и 4016 (нижний индекс означает основание системы счисления).
Содержание
История
В Индии
Индийцы называли знак, обозначающий отсутствие какого-либо разряда в числе, словом «сунья», что значит пустой (разряд, место, см. Шуньята). Арабы перевели это слово по смыслу и получили слово «сифр».
Первое достоверное свидетельство о записи нуля относится к 876 г.; в настенной надписи из Гвалиора (Индия) имеется число 270. Некоторые исследователи предполагают, что нуль быль заимствован у греков, которые ввели в качестве нуля букву «о» в шестидесятеричную систему счисления, употребляемую ими в астрономии.
Другие, наоборот, считают, что ноль пришёл в Индию с востока, он был изобретён на границе индийской и китайской культур. Обнаружены более ранние надписи от 683 и 686 гг. в нынешних Камбодже и Индонезии, где нуль изображён в виде точки и малого кружка.
Индийцы вначале обозначали нуль точкой.
В Европе
Леонардо Пизанский (1228) употребил для передачи арабского термина «сифр» слово zephirum (латинское слово zephyrus — зефир означало западный ветер), а одновременно с ним другой главный поборник индийской нумерации в Европе, Иордан Неморарий (1237), употребляет арабскую форму cifra.
С начала XVI века в немецких руководствах слово «цифра» получает значение современное, слово «нуль» входит в повсеместное употребление в Германии и в других странах, сначала как слово чужое и в латинской грамматической форме, постепенно принимая форму, свойственную данному национальному языку.
В России
Ноль в других культурах
Майя использовали ноль в своей двадцатеричной системе счисления почти на тысячелетие раньше индийцев. Первая сохранившаяся стела с датой календаря майя датируется 7.16.3.2.13, 6 Бен 16 Шуль 10 декабря 36 года до н. э..
В империи инков Тауантинсуйу для записи числовой информации использовалась узелковая система кипу, основанная на позиционной десятеричной системе счисления. Цифры от 1 до 9 обозначались узелками определённого вида, ноль — пропуском узелка в нужной позиции. В современном кечуа ноль обозначается словом кечуа ch’usaq (букв. «отсутствующий», «пустой»), однако то, какое слово использовалось инками для обозначения нуля при чтении кипу, пока неясно, поскольку, например, в одних из первых кечуа-испанских (Диего Гонсалес Ольгин, 1608) словарях и первом аймара-испанском (Лудовико Бертонио, 1612) не было соответствия для испанского «cero» — «ноль».







