Как назвать математику по другому
Разделы математики
Существует три официальных способа подразделения математики.
Содержание
Математика как специальность
Математика как специальность научных работников министерства науки и технологий Российской Федерации [1] подразделяется на научные специальности
Математика как учебная дисциплина
Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе, и образованную дисциплинами:
и высшую математику, изучаемую в ВУЗе. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности. Программа обучения по специальности математика [2] образована следующими учебными дисциплинами:
Знаком (ф) отмечены дисциплины, которые изучаются при обучении по специальности «физика».
Систематизация научных работ
Для систематизации научных работ используется Универсальная десятичная классификация 51.
Примечания
Полезное
Смотреть что такое «Разделы математики» в других словарях:
МАТЕМАТИКИ ИСТОРИЯ — Самой древней математической деятельностью был счет. Счет был необходим, чтобы следить за поголовьем скота и вести торговлю. Некоторые первобытные племена подсчитывали количество предметов, сопоставляя им различные части тела, главным образом… … Энциклопедия Кольера
История математики — История науки … Википедия
История математики в России — Данная статья часть обзора История математики. Содержание 1 Древность и средневековье 2 XVII век 3 … Википедия
Философия математики — учение о сущности математического знания и о базовых принципах математических доказательств, раздел философии науки; её можно также назвать «метаматематикой». Содержание 1 Возможность оснований математики 2 Литература … Википедия
История математики в Индии — Данная статья часть обзора История математики. Научные достижения индийской математики широки и многообразны. Уже в древние времена учёные Индии на своём, во многом оригинальном пути развития достигли высокого уровня математических знаний.… … Википедия
Институт математики и механики (НИИММ СПбГУ) — Научно исследовательский институт математики и механики имени академика В. И. Смирнова (НИИММ СПбГУ) структурное подразделение Санкт Петербургского государственного университета. Выполняет организационную роль, является материальной базой для… … Википедия
Математика — Евклид. Деталь «Афинской школы» Рафаэля Математика (от др. греч … Википедия
Дискретная математика — Дискретная математика область математики, занимающаяся изучением дискретных структур, которые возникают как в пределах самой математики, так и в её приложениях. К числу таких структур могут быть отнесены конечные группы, конечные графы, а… … Википедия
Математический анализ — У этого термина существуют и другие значения, см. Анализ. Математический анализ совокупность разделов математики, посвящённых исследованию функций и их обобщений методами дифференциального и интегрального исчислений. При столь общей… … Википедия
МЕТОД АКСИОМАТИЧЕСКИЙ — способ построения теории, при к ром в ее основу кладутся нек рые ее положения – аксиомы или постулаты, – из к рых все остальные положения теории (теоремы) выводятся путем рассуждений, называемых д о к а з а т е л ь с т в а м и. Правила, по к рым… … Философская энциклопедия
Математика
Содержание
Основные сведения
Идеализированные свойства исследуемых объектов либо формулируются в виде аксиом, либо перечисляются в определении соответствующих математических объектов. Затем по строгим правилам логического вывода из этих свойств выводятся другие истинные свойства (теоремы). Эта теория в совокупности образует математическую модель исследуемого объекта. Таким образом первоначально, исходя из пространственных и количественных соотношений, математика получает более абстрактные соотношения, изучение которых также является предметом современной математики.
Традиционно математика делится на теоретическую, выполняющую углублённый анализ внутриматематических структур, и прикладную, предоставляющую свои модели другим наукам и инженерным дисциплинам, причём некоторые из них занимают пограничное с математикой положение. В частности, формальная логика может рассматриваться и как часть философских наук, и как часть математических наук; механика — и физика, и математика; информатика, компьютерные технологии и алгоритмика относятся как к инженерии, так и к математическим наукам и т. д. В литературе было предложено много различных определений математики (см. ниже).
Этимология
В текстах на русском языке слово «математика» или «мафематика» встречается по крайней мере с XVII века, например, у Николая Спафария в «Книге избранной вкратце о девяти мусах и о седмих свободных художествах» (1672 год) [5]
Определения
Одно из первых определений предмета математики дал Декарт [6] :
К области математики относятся только те науки, в которых рассматривается либо порядок, либо мера и совершенно не существенно, будут ли это числа, фигуры, звёзды, звуки или что-нибудь другое, в чём отыскивается эта мера. Таким образом, должна существовать некая общая наука, объясняющая всё относящееся к порядку и мере, не входя в исследование никаких частных предметов, и эта наука должна называться не иностранным, но старым, уже вошедшим в употребление именем Всеобщей математики.
Математика… наука о количественных отношениях и пространственных формах действительного мира.
Это определение Энгельса [8] ; правда, далее Колмогоров поясняет, что все использованные термины надо понимать в самом расширенном и абстрактном смысле.
Сущность математики… представляется теперь как учение об отношениях между объектами, о которых ничего не известно, кроме описывающих их некоторых свойств,— именно тех, которые в качестве аксиом положены в основание теории… Математика есть набор абстрактных форм — математических структур.
Приведём ещё несколько современных определений.
Герман Вейль пессимистически оценил возможность дать общепринятое определение предмета математики:
Вопрос об основаниях математики и о том, что представляет собой в конечном счёте математика, остаётся открытым. Мы не знаем какого-то направления, которое позволит в конце концов найти окончательный ответ на этот вопрос, и можно ли вообще ожидать, что подобный «окончательный» ответ будет когда-нибудь получен и признан всеми математиками.
Разделы математики
1. Математика как учебная дисциплина подразделяется в Российской Федерации на элементарную математику, изучаемую в средней школе и образованную дисциплинами:
и высшую математику, изучаемую на нематематических специальностях вузов. Дисциплины, входящие в состав высшей математики, варьируются в зависимости от специальности.
Программа обучения по специальности математика [13] образована следующими учебными дисциплинами:
2. Математика как специальность научных работников Министерством образования и науки Российской Федерации [14] подразделяется на специальности:
3. Для систематизации научных работ используется раздел «Математика» [15] универсальной десятичной классификации (УДК).
4. Американское математическое общество (AMS) выработало свой стандарт для классификации разделов математики. Он называется Mathematics Subject Classification. Этот стандарт периодически обновляется. Текущая версия — это MSC 2010. Предыдущая версия — MSC 2000.
Обозначения
Вследствие того, что математика работает с чрезвычайно разнообразными и довольно сложными структурами, система обозначений также очень сложна. Современная система записи формул сформировалась на основе европейской алгебраической традиции, а также математического анализа (понятия функции, производной и т. д.). Геометрия испокон века пользовалась наглядным (геометрическим же) представлением. В современной математике распространены также сложные графические системы записи (например, коммутативные диаграммы), нередко также применяются обозначения на основе графов.
Краткая история
Академиком А. Н. Колмогоровым предложена такая структура истории математики:
Развитие математики началось вместе с тем, как человек стал использовать абстракции сколько-нибудь высокого уровня. Простая абстракция — числа; осмысление того, что два яблока и два апельсина, несмотря на все их различия, имеют что-то общее, а именно занимают обе руки одного человека, — качественное достижение мышления человека. Кроме того, что древние люди узнали, как считать конкретные объекты, они также поняли, как вычислять и абстрактные количества, такие, как время: дни, сезоны, года. Из элементарного счёта естественным образом начала развиваться арифметика: сложение, вычитание, умножение и деление чисел.
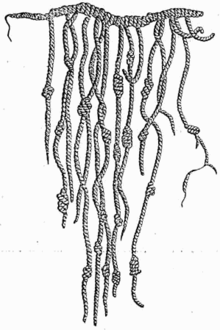
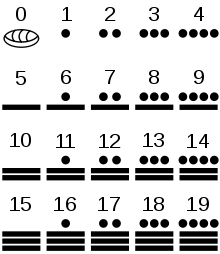
Развитие математики опирается на письменность и умение записывать числа. Наверно, древние люди сначала выражали количество путём рисования чёрточек на земле или выцарапывали их на древесине. Древние инки, не имея иной системы письменности, представляли и сохраняли числовые данные, используя сложную систему верёвочных узлов, так называемые кипу. Существовало множество различных систем счисления. Первые известные записи чисел были найдены в папирусе Ахмеса, созданном египтянами Среднего царства. Индская цивилизация разработала современную десятичную систему счисления, включающую концепцию нуля.
Исторически основные математические дисциплины появились под воздействием необходимости вести расчёты в коммерческой сфере, при измерении земель и для предсказания астрономических явлений и, позже, для решения новых физических задач. Каждая из этих сфер играет большую роль в широком развитии математики, заключающемся в изучении структур, пространств и изменений.
Философия математики
Цели и методы
Математика изучает воображаемые, идеальные объекты и соотношения между ними, используя формальный язык. В общем случае математические понятия и теоремы не обязательно имеют соответствие чему-либо в физическом мире. Главная задача прикладного раздела математики — создать математическую модель, достаточно адекватную исследуемому реальному объекту. Задача математика-теоретика — обеспечить достаточный набор удобных средств для достижения этой цели.
Содержание математики можно определить как систему математических моделей и инструментов для их создания. Модель объекта учитывает не все его черты, а только самые необходимые для целей изучения (идеализированные). Например, изучая физические свойства апельсина, мы можем абстрагироваться от его цвета и вкуса и представить его (пусть не идеально точно) шаром. Если же нам надо понять, сколько апельсинов получится, если мы сложим вместе два и три, — то можно абстрагироваться и от формы, оставив у модели только одну характеристику — количество. Абстракция и установление связей между объектами в самом общем виде — одно из главных направлений математического творчества.
Другое направление, наряду с абстрагированием — обобщение. Например, обобщая понятие «пространство» до пространства n-измерений. «Пространство 

Изучение внутриматематических объектов, как правило, происходит при помощи аксиоматического метода: сначала для исследуемых объектов формулируются список основных понятий и аксиом, а затем из аксиом с помощью правил вывода получают содержательные теоремы, в совокупности образующие математическую модель.
Основания
Вопрос сущности и оснований математики обсуждался со времён Платона. Начиная с XX века наблюдается сравнительное согласие в вопросе, что надлежит считать строгим математическим доказательством, однако отсутствует согласие в понимании того, что в математике считать изначально истинным. Отсюда вытекают разногласия как в вопросах аксиоматики и взаимосвязи отраслей математики, так и в выборе логических систем, которыми следует при доказательствах пользоваться.
Помимо скептического, известны нижеперечисленные подходы к данному вопросу.
Теоретико-множественный подход
Предлагается рассматривать все математические объекты в рамках теории множеств, чаще всего с аксиоматикой Цермело — Френкеля (хотя существует множество других, равносильных ей). Данный подход считается с середины XX века преобладающим, однако в действительности большинство математических работ не ставят задач перевести свои утверждения строго на язык теории множеств, а оперируют понятиями и фактами, установленными в некоторых областях математики. Таким образом, если в теории множеств будет обнаружено противоречие, это не повлечёт за собой обесценивание большинства результатов.
Логицизм
Данный подход предполагает строгую типизацию математических объектов. Многие парадоксы, избегаемые в теории множеств лишь путём специальных уловок, оказываются невозможными в принципе.
Формализм
Данный подход предполагает изучение формальных систем на основе классической логики.
Интуиционизм
Интуиционизм предполагает в основании математики интуиционистскую логику, более ограниченную в средствах доказательства (но, как считается, и более надёжную). Интуиционизм отвергает доказательство от противного, многие неконструктивные доказательства становятся невозможными, а многие проблемы теории множеств — бессмысленными (неформализуемыми).
Конструктивная математика
Основные темы
Числа
Понятие «число» первоначально относилось к натуральным числам. В дальнейшем оно было постепенно распространено на целые, рациональные, действительные, комплексные и другие числа.
| |||||||||||||||
 |  | ||||||||||||||
| Комплексные числа | Кватернионы | ||||||||||||||
 Числовые системы Числовые системы | |
|---|---|
| Счётные множества | Натуральные числа ( ) • Целые ( ) • Целые ( ) • Рациональные ( ) • Рациональные ( ) • Алгебраические ( ) • Алгебраические ( ) • Периоды • Вычислимые • Арифметические ) • Периоды • Вычислимые • Арифметические |
| Вещественные числа и их расширения | Вещественные ( ) • Комплексные ( ) • Комплексные ( ) • Кватернионы ( ) • Кватернионы ( ) • Числа Кэли (октавы, октонионы) ( ) • Числа Кэли (октавы, октонионы) ( ) • Седенионы ( ) • Седенионы ( ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) ) • Альтернионы • Процедура Кэли — Диксона • Дуальные • Гиперкомплексные • Суперреальные • Гиперреальные • Surreal number (англ.) |
| Другие числовые системы | Кардинальные числа • Порядковые числа (трансфинитные, ординал) • p-адические • Супернатуральные числа |
| См. также | Двойные числа • Иррациональные числа • Трансцендентные • Числовой луч • Бикватернион |
Преобразования
 | 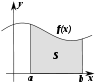 |  |  |
| Арифметика | Дифференциальное и интегральное исчисление | Векторный анализ | Анализ |
 |  |  | |
| Дифференциальные уравнения | Динамические системы | Теория хаоса |
Структуры
Пространственные отношения
Более наглядные подходы в математике.
Дискретная математика
Дискретная математика включает средства, которые применяются над объектами, способными принимать только отдельные, не непрерывные значения.
 |  |  |  |
| Математическая логика | Теория вычислимости | Криптография | Теория графов |
Коды в системах классификации знаний
Онлайновые сервисы
Существует большое число сайтов, предоставляющих сервис для математических расчётов. Большинство из них англоязычные. [20] Из русскоязычных можно отметить сервис математических запросов поисковой системы Nigma.
16 известных и величайших математиков
Кто из величайших и самых известных математиков когда-либо жил? Что ж, его ответ нелегок, поскольку математика была известна человечеству с доисторических времен, задолго до рождения Христа.
Роль математики в нашей жизни огромна. Математика позволила передавать электричество на тысячи километров, помогла изучить концепцию ДНК, породила компьютеры, и в нашем стремлении лучше понять вселенную.
Без математики ученые не могут разрабатывать лучшие лекарства, а инженеры не могут исследовать новые технологии. У этого списка нет конца.
Как и большинство вещей, математика, которую мы знаем сегодня, возникла не просто случайно. Математикам требуются десятилетия, чтобы сформулировать новую революционную теорему и уравнение. Так кто же эти математики? Давайте разберемся.
16. Сриниваса Рамануджан
Известен: гипотеза Рамануджана – Петерссона; Основная теорема Рамануджана
Сриниваса Рамануджан был, пожалуй, самым замечательным математиком в современной Индии. Хотя Рамануджан не имел формальной подготовки, его продвинутые математические знания в очень молодом возрасте приводили многих в замешательство.
К 16 годам он смог изучать числа Бернулли, которые он сам разработал, и рассчитал постоянную Эйлера-Маскерони. Перед смертью в молодом возрасте 32 лет Рамануджан успешно собрал почти 4000 различных математических тождеств.
Он приобрел международную известность после того, как выдающийся британский математик Дж. Харди узнал его работу и сравнил его с такими, как Эйлер и Якоби.
15. Жозеф-Луи Лагранж
Известен: Лагранжевой механики; Небесная механика; Теория чисел
Джозеф Лагранж был одним из самых заметных учеников великого Леонарда Эйлера. Лагранж начал свою математическую карьеру с вариационного исчисления (в 1754 году), которое привело к формулировке уравнения Эйлера – Лагранжа.
Лагранж переформулировал классическую механику, чтобы представить механику Лагранжа несколько лет спустя. Его знаменитая работа по аналитической механике (Mécanique analytique) помогла другим исследователям развить область математической физики.
14. Эндрю Уайлс
Награды: Приз Волка (1995/6); Премия Абеля (2016)
Сэр Эндрю Джон Уайлс — британский математик, наиболее известный тем, что доказал последнюю теорему Ферма, некогда считавшуюся «самой сложной математической проблемой».
В 1975 году под руководством Джона Х. Коутса Эндрю Уайлс начал работать над теорией Ивасавы, которую он продолжил с американским математиком Барри Мазуром.
Однако его крупнейший прорыв произошел в начале 1990-х, когда он смог доказать большую часть теоремы модульности (ранее гипотеза Танияма-Шимура). Теорема модульности, по сути, связана с последней теоремой Ферма и была достаточной для ее доказательства.
Мистер Уайлз в настоящее время работает профессором-исследователем в Оксфордском университете.
13. Карл Густав Джейкоб Якоби
Известен: эллиптических функций Якоби; Преобразование Якоби
Кроме того, он внес фундаментальный вклад в области механической динамики и теории чисел.
12. Алан Тьюринг
Известен: Криптоанализ загадки, Доказательства Тьюринга, премия Смита (1936)
Во время Второй мировой войны немецкая разведывательная сеть считалась почти непробиваемой. Многие союзные страны боялись, что, если они не смогут перехватить важные передачи нацистского верховного командования, они могут в конечном итоге проиграть войну.
После окончания войны Тьюринг присоединился к Национальной физической лаборатории (Великобритания), где он разработал автоматический вычислительный движок, один из самых ранних компьютеров с хранимой программой.
11. Г.Ф. Бернхард Риман
Известен: интеграл Римана; Ряд Фурье
Георг Бернхард Риман родился в небольшой деревне недалеко от Данненберга, Германия. Под руководством Карла Фридриха Гаусса Риман изучал дифференциальную геометрию и выдвигал свою теорию дополнительных или более высоких измерений. Его работа теперь известна как риманова геометрия.
На Римана оказал сильное влияние Иоганн Густав Дирихле, который также оказал влияние на его математическую карьеру. Только используя принцип Дирихле, он смог сформулировать знаменитую теорему Римана о отображении.
Некоторые из его математических уравнений были позже использованы Эйнштейном в его общей теории относительности.
10. Анри Пуанкаре
Анри Пуанкаре Генри Пуанкаре вместе с Мари Кюри на Сольвеевской конференции 1911 года
Известен: проблема с тремя телами; Теория хаоса; Теорема Пуанкаре – Хопфа
По словам Эрика Белла, известного шотландского математика, Анри Пуанкаре был, вероятно, одним из последних универсалистов, поскольку в то время он процветал почти во всех известных областях математики.
В течение своей жизни Пуанкаре внес многочисленные теории в области математической физики, прикладной математики и астрономии. Он сыграл важную роль в разработке теории специальной теории относительности.
Более того, его исключительные работы по преобразованию Лоренца и проблеме трех тел проложили путь математикам, а также астрофизикам к открытиям о нашей планете и космосе. Его теоретические работы даже вдохновили известных художников, таких как Пикассо и Брак, создать художественное движение (кубизм) в 20-м веке.
9. Дэвид Гильберт
Известен: теории доказательств; Проблемы Гильберта
Дэвид Гильберт был, пожалуй, самым известным математиком времени. Он сыграл важную роль в разработке фундаментальных теорий в области коммутативной алгебры, вариационного исчисления и математической физики.
Проблемы Гильберта (набор из двадцати трех математических задач, которые он опубликовал в 1900 году) повлияли на новаторские исследования в различных областях математики. Некоторые из этих проблем до сих пор не решены.
В последние дни Дэвид Гильберт посвятил себя физике. Именно в это время он соревновался с Альбертом Эйнштейном в общей теории относительности.
8. Фибоначчи
Известен по: числам Фибоначчи
Фибоначчи, также известный как Леонардо из Пизы, был одним из самых опытных математиков высокого средневековья.
Возможно, его самым важным вкладом в этот предмет является книга Либера Абачи, в которой он популяризировал индо-арабскую систему счисления (0,1,2,3,4. ) и последовательность Фибоначчи в Европе.
Последовательность Фибоначчи используется в компьютерных алгоритмах и базах данных.
7. Семья Бернулли
В мире математики семья Бернулли занимает особое место. Родом из Антверпена (Бельгия), Джейкоб и его брат Иоганн Бернулли были первыми математиками в этой семье.
И Джейкоб, и Иоганн работали вместе над бесконечно малым исчислением, и им приписывают теоремы и обоснования, такие как числа Бернулли и кривая Брахистохрона.
Даниэль Бернулли, сын Джейкоба, был одним из самых выдающихся членов семьи Бернулли. Его наиболее известная работа, принцип Бернулли, математически объясняет работу карбюратора и крыла самолета. Он также внес существенный вклад в области вероятности и статистики.
6. Пифагор
Пифагор (пишет книгу), изображенный на фреске Рафаэля «Афинская школа»
Известен: теорема Пифагора; Теория Пропорций
Пифагор Самосский родился около 570 г. до н.э. Как и большинство древних греков, о его молодости известно немногое. Как философ, его работы оказали влияние на Платона и Аристотеля, а также на Иоганна Кеплера и Исаака Ньютона.
Пифагор, возможно, также был ответственен за открытие Теории Пропорций.
5. Карл Фридрих Гаусс
Награды: премия Лаланде (1809), медаль Копли (1838)
Карл Фридрих Гаусс был, пожалуй, самым влиятельным математиком со времен древних греков. Его вклад в различные области математики и физики практически не имеет аналогов. Гаусс начал проявлять математические способности в возрасте семи лет, когда он мог решать арифметические прогрессии намного быстрее, чем кто-либо в своем классе.
Некоторые из его популярных работ включают Закон Гаусса и Теорема Egregium, в которых сделан вывод, что Земля не может быть отображена на карте без искажений. Он был первым, кто предположил возможность неевклидовой геометрии, хотя его работы никогда не публиковались.
4. Иссак Ньютон
Известен: законы движения Ньютона; Исчисление; Ньютоновская механика
Сэр Иссак Ньютон является одним из основателей классической механики, а также исчисления бесконечно малых. Его взгляды на гравитацию оставались общепринятыми до теории относительности Эйнштейна.
Самый замечательный вклад Ньютона в математику — исчисление (тогда называемое бесконечно малыми), которое он разработал независимо от своего современника Готфрида Вильгельма Лейбница.
Это был Ньютон, который первым объяснил причину приливных возмущений на Земле и помог проверить закономерности движения планет Кеплера. Его работы по оптике дали нам первый в мире преломляющий телескоп.
3. Леонард Эйлер
Известен: догадки Эйлера; Уравнения Эйлера; Числа Эйлера
Сегодня математики высоко ценят Эйлера и считают его самым важным математиком 18-го века.
Эйлер внес значительный вклад почти во все основные области математики, включая алгебру, тригонометрию и геометрию. В физике его работы по гидродинамике и рядам Фурье не имеют себе равных.
2. Архимед
Известен: принцип Архимеда; гидростатика
Архимед родился примерно в 287 г. до н.э. в Сиракузах, Сицилия. Он хорошо разбирался в математике, физике и астрономии того времени. Он был эрудитом. Однако большинство его литературных произведений не сохранилось.
Архимед был одним из пионеров геометрии, который вывел формулы для площади круга, объема и площади поверхности сферы. Его метод определения значения числа пи оставался бесспорным и единственным известным способом вычисления окружности круга на протяжении десятилетий.
Филдса, самая высокая честь в области математики, несет портрет (справа облицовочный) Архимед вместе с цитатой приписываемой ему.
1. Евклид
Известен: евклидовой геометрии; Евклидов алгоритм
Евклид Александрийский был греческим математиком, которого многие считают основателем геометрии. Euclid’s Elements, сборник из 13 книг, считается одной из самых старых и влиятельных книг по математике.
Хотя геометрия (которая теперь известна как евклидова геометрия) является фокусом в Элементах Евклида, она также имеет всеобъемлющее введение в теорию элементарных чисел. Его работы по оптике также получили широкое признание.