Как на рисунке изображается направление вектора

Векторы

Векторы могут быть графически представлены направленными отрезками. Длина выбирается по определенной шкале, чтобы обозначить величину вектора, а направление отрезка представляетнаправление вектора. Например, если мы примем, что 1 см представляет 5 км/час, тогда северо-восточный ветер со скоростью 15 км/час будет представлен направленным отрезком длиной 3 cм, как показано на рисунке.

Вектор на плоскости это направленный отрезок. Два вектора равны если они имеют одинаковуювеличину и направление.

Рассмотрим вектор, нарисованный из точки A к точке B. Точка называется начальной точкой вектора, а точка B называется конечной точкой. Символическим обозначением для этого вектора есть (читается как “вектора AB”). Векторы также обозначается жирными буквами, такими как U, V и W. Четыре вектора на рисунке слева имеют одинаковую длину и направление. Поэтому они представляют равные веторы; то есть,

В контексте векторов мы применяем = чтобы обозначить их равность.

Длина, или величина выражается как ||. Для того, чтобы определить, равны ли векторы, мы находим их величины и направления.

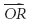
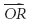
Пример 1 Векторы u, , w показаны на рисунке внизу. Докажите, что u = = w.

Предположим, что человек делает 4 шага на восток, а затем 3 шага на север. Тогда человек будет в 5 шагах от начальной точки в направлении, показанном слева. Вектор в 4 единицы длиной и с направление направо представляет 4 шага на восток и вектор 3 единицы длиной направление вверх представляет 3 шага на север. Сумма двух этих векторов есть вектор 5-ти шагов величины и в показанном направлении. Сумма также называется результирующим двух векторов.

В общем, два ненулевых вектора u и v могут быть сложены геометрически расположением начальной точки вектора v в конечную точку вектора u, и затем нахождением ветора, который имеет ту же самую начальную точку, что и вектор u и ту же самую конечную точку что и вектор v, как показано на рисунке внизу.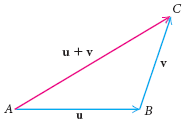

Суммой есть вектор, представленный направленным отрезком из точки A вектора u в конечную точку C вектора v. Таким образом, если u = и v = , тогда
u + v = + =

Мы также можем описать сложение векторов как совместное размещение начальных точек векторов, построением параллелограмма и нахождением диагонали параллелограмма. (на рисунке внизу.) Это сложение иногда называется как правило параллелограмма сложения векторов. Векторное сложение коммутативно. Как показано на рисунке, оба вектора u + v и v + u представлены одним и тем же направленным отрезком.

Если две силы F₁ и F₂ действуют на один объект, результирующая сила есть сумма F₁ + F₂ этих двух отдельных сил.

Пример Две силы в 15 ньютонов и 25 ньютонов действуют на один объект перпендикулярно друг другу. Найдите их сумму, или результирующую силу и угол, которая она образовывает с большей силой.

Пилоты могут корректировать направление их полёта, если есть боковой ветер. Ветер и скорость самолёта могут быть изображены как веторы.

Если нам задан вектор w, мы можем найти два других вектора u и v, сумма которых есть w. Векторы u и v называются компонентами w и процесс их нахождения называется разложением, или представлением вектора его векторными компонентами.

Пример 4 Вектор w имеет величину 130 и наклон 40° относительно горизонтали. Разложите вектор на горизонтальные и вертикальные компоненты.

Решение Сначала мы нарисуем рисунок с горизонтальными и вертикальными векторами u и v, чья сумма есть w.

Из ABC, мы находим |u| и |v|, используя определения косинуса и синуса:
cos40° = |u|/130, или |u| = 130.cos40° ≈ 100,
sin40° = |v|/130, или |v| = 130.sin40° ≈ 84.
Тогда, горизонтальная компонента w есть 100 направо и вертикальная компонента w есть 84 вверх.

Источник

Определение вектора

В статье пойдет речь о том, что такое вектор, что он из себя представляет в геометрическом смысле, введем вытекающие понятия.

Для начала дадим определение:

Вектор – это направленный отрезок прямой.

Исходя из определения, под вектором в геометрии отрезок на плоскости или в пространстве, который имеет направление, и это направление задается началом и концом.

Нулевой вектор

Под нулевым вектором 0 → будем понимать любую точку плоскости или пространства.

Из определения становится очевидным, что нулевой вектор может иметь любое направление на плоскости и в пространстве.

Длина вектора

Под длиной вектора A B → понимается число, большее либо равное 0, и равное длине отрезка АВ.

Понятия модуль вектора и длина вектора равносильны, потому что его обозначение совпадает со знаком модуля. Поэтому длину вектора также называют его модулем. Однако грамотнее использовать термин «длина вектора». Очевидно, что длина нулевого вектора принимает значение ноль.

Коллинеарность векторов

Два вектора лежащие на одной прямой или на параллельных прямых называются коллинеарными.

Два вектора не лежащие на одной прямой или на параллельных прямых называются неколлинеарными.

Следует запомнить, что Нулевой вектор всегда коллинеарен любому другому вектору, так как он может принимать любое направление.

Коллиниарные векторы в свою очередь тоже можно разделить на два класса: сонаправленные и противоположно направленные.

Направление векторов

Считается, что нулевой вектор является сонаправленым к любым другим векторам.

Равные и противоположные векторы

Равными называются сонаправленные вектора, у которых длины равны.

Противопожными называются противоположно направленные вектора, у которых их длины равны.

Введенные выше понятия позволяют нам рассматривать векторы без привязки к конкретным точкам. Иначе говоря, можно заменить вектор равным ему вектором, отложенным от любой точки.

Углы между векторами

Угол φ = ∠ A O B называется углом между векторами a → = O A → и b → = O B → .

Очевидно, что угол между сонаправленными векторами равен нулю градусам (или нулю радиан), так как сонаправленные векторы лежат на одной или на параллельных прямых и имеют одинаковое направление, а угол между противоположно направленными векторами равен 180 градусам (или π радиан), так как противоположно направленные векторы лежат на одной или на параллельных прямых, но имеют противоположные направления.

Перпендикулярными называются два вектора, угол между которыми равен 90 градусам (или π 2 радиан).

Источник

Характеристики вектора: длина, направление, координаты

У любого вектора есть 2 главные характеристики:

Третья характеристика вектора – это его координаты.

Примечание:

Зная координаты вектора, можно найти его длину и направление. Поэтому, задавать информацию о векторе можно двояко: либо указав его длину и направление, либо его координаты.

Что такое координаты вектора

Координаты вектора – это длины его теней на осях координат (его проекции на оси).

Координаты вектора указывают так:

\( a_ \) – это «x» координата вектора, проекция вектора \( \vec \) на ось Ox;

\( a_ \) — это «y» координата вектора, проекция вектора \( \vec \) на ось Oy;

Координаты вектора можно получить из координат его начальной и конечной точек:

«координата вектора» = «конец» — «начало»

Пример:

\( A \left( 1;1 \right) \) — начальная точка,

\( B \left( 4;3 \right) \) — конечная точка,

\[ \overrightarrow = \left\< AB_; AB_ \right\> \]

\[ \begin AB_ = 4 – 1; AB_ = 3 \\ AB_ = 3 – 1; AB_ = 2 \end \]

Длина вектора (в чем измеряется, как посчитать)

Длину вектора (его модуль) обозначают так:

Как вычислить длину вектора по его координатам

Когда известны координаты вектора, его длину считают так:

\( a_ \) и \( a_ \) — это числа, координаты вектора \( \vec \)

Для двухмерного вектора:

Для трехмерного вектора:

Как вычислить длину вектора с помощью рисунка

Если вектор нарисован на клетчатой бумаге, длину считаем так:

1). Если вектор лежит на линиях клеточек тетради:

— считаем количество клеточек.

Зная масштаб клеток, легко получить длину вектора – умножаем масштаб на количество клеток.

2). Если вектор не лежит вдоль линий:

— проводим вертикаль и горизонталь пунктиром.

\( \Delta x \) — горизонталь; \( \Delta y \) — вертикаль;

— затем применяем формулу:

Как указать направление вектора

Указать направление вектора можно с помощью его координат. Так как в его координатах уже содержится информация о длине и направлении вектора.

Бывает так, что координаты вектора неизвестны, а известна только лишь его длина. Тогда направление можно указать с помощью угла между вектором и какой-либо осью.

Для двумерного вектора

Если вектор двумерный, то для указания направления (см. рис. 10) можно использовать один из двух углов:

Словами указать направление вектора можно так:

Такой способ указания координат используют в полярной системе координат.

Для трехмерного вектора

Когда вектор располагается в трехмерном пространстве, чтобы указать, куда вектор направлен, используют два угла.

Такой способ указания координат используют в сферической системе координат.

Считаем Землю шаром. Расположим ее центр в начале трехмерной системы координат – точке (0 ; 0 ; 0).

Тогда координаты любой точки на поверхности планеты можно указать с помощью радиус-вектора этой точки.

Для указания сферических координат принято использовать:

Источник

Вектор. Виды векторов.

Вектор — в самом элементарном случае это математический объект, который характеризуется

величиной и направлением.

В геометрии вектор — направленный отрезок прямой, то есть отрезок, для которого указано, какая

из его граничных точек является началом, а какая — концом.

У вектора есть длина и определенное направление. Графически вектора изображаются как

направленные отрезки прямой конкретной длины. Длина вектора – это и есть длина этого отрезка.

Для обозначения длины вектора используются две вертикальные линии по обоим сторонам: |AB|.

Как видно на рисунке, начало отрезка – это точка А, концом отрезка является

точка В, а непосредственно вектор обозначен через . У направления

вектора существенное значение, если переместить стрелку на другую

сторону отрезка, то получим вектор, но абсолютно другой. Понятие вектора

удобно сравнивать с движением физического тела: подумайте, ехать на

рыбалку и с рыбалки – разница огромная.

Понятия «больше» и «меньше» для векторов не имеет значения — так как направления их могут быть

разными. Сравнивают лишь длины векторов. Зато есть понятие равенства для векторов.

Виды векторов.

Единичным называется вектор, длина которого равна 1.

Отдельные точки плоскости, пространства удобно считать так называемым нулевым вектором.

У такого вектора конец и начало совпадают.

Нулевой вектор обычно обозначается как . Длина нулевого вектора, или его модуль равен нулю.

Коллинеарные вектора – вектора, которые параллельны одной прямой

или которые лежат на одной прямой.

Сонаправленные вектора. Два коллинеарных вектора a и b называются

сонаправленными векторами только тогда, когда их направления

соответствуют друг другу: a↑↑b

Противоположно направленные вектора – два коллинеарных вектора

a и b называются противоположно направленными векторами, только

когда они направлены в разные стороны: a↑↓b.

Компланарные вектора – это те вектора, которые параллельны одной

плоскости или те, которые лежат на общей плоскости.

В любое мгновение существует плоскость одновременно параллельную

двум любым векторам, поэтому два произвольных вектора являются

Равные вектора. Вектора a и b будут равными, если они будут лежать на

одной либо параллельных прямых и их направления и длины одинаковые.

То есть, такой вектор можно перенести параллельно ему в каждое место

Таким образом, два вектора равны, если они коллинеарные, сонаправленые

и имеют одинаковые длины:

Для координатного представления векторов огромное значение

оказывает понятие проекции вектора на ось (направленную

прямую).

проекциями точек начала и конца вектора на заданную прямую,

при этом проекции добавляется знак “+”, но когда направление

проекции соответственно направлению оси, иначе — знак “–”.

Проекция – это длина заданного вектора, умноженная на cos угла исходного вектора и оси; проекция

вектора на ось, которая перпендикулярна ему = 0.

Когда работают с векторами, зачастую вводят так называемую

декартову систему координат и уже в этой системе находят

координаты вектора по базисным векторам.

Разложение по базису геометрически можно показать проекцией

вектора на координатные оси. Когда известны координаты начала и

конца вектора, то координаты данного вектора получают вычитая

из координат конца вектора координат начала вектора.

За базис зачастую выбираются координатные орты, которые обозначаются как , соответственно

осям x, y, z. Исходя из этого, вектор можно записать в таком виде:

Каждое геометрическое свойство есть возможность записать в координатах, и далее исследование

из геометрического переходит в алгебраическое и на этом этапе в основном упрощается. Обратное,

кстати, неверно: не у любого соотношения в координатах есть геометрическое толкование, но только

те соотношения, которые выполняются в любой декартовой системе координат (инвариантные).

Источник

Вектор, его направление и длина

Вектором называется упорядоченная пара точек. Первая точка называется началом вектора, вторая — концом вектора. Расстояние между началом и концом вектора называется его длиной. Вектор, начало и конец которого совпадают, называется нулевым, его длина равна нулю. Если длина вектора положительна, то его называют ненулевым. Ненулевой вектор можно определить также как направленный отрезок, т.е. отрезок, у которого одна из ограничивающих его точек считается первой (началом вектора), а другая — второй (концом вектора). Направление нулевого вектора, естественно, не определено.

Ненулевой вектор АВ кроме направленного отрезка определяет также содержащие его луч (с началом в точке ) и прямую (рис.1.1,а).

Коллинеарные векторы

Два ненулевых коллинеарных вектора называются одинаково направленными (сонаправленными), если они принадлежат параллельным прямым и их концы лежат в одной полуплоскости от прямой, проходящей через их начала (рис.1.2,а); либо, если векторы принадлежат одной прямой, и луч, определяемый одним вектором, целиком принадлежит лучу, определяемому другим вектором (рис. 1.2,6). В противном случае коллинеарные векторы называются противоположно направленными (рис.1.2,в,г). Одинаково направленные и противоположно направленные векторы обозначаются парами стрелок и соответственно. Понятия коллинеарных, одинаково направленных векторов распространяются на любое число векторов.

Компланарные векторы

Три ненулевых вектора называются компланарными, если они лежат в одной плоскости или в параллельных плоскостях (рис.1.3,а), в противном случае они называются некомпланарными (рис. 1.3,6). Так как направление нулевого вектора не определено, он считается компланарным с любыми двумя векторами. Понятие компланарных векторов распространяется на любое число векторов.

Равные векторы

Два вектора называются равными, если они:

а) коллинеарны, одинаково направлены;

б) имеют равные длины.

Все нулевые векторы считаются равными друг другу.

Это определение равенства векторов характеризует так называемые свободные векторы. Данный свободный вектор можно переносить, не меняя его направления и длины, в любую точку пространства (откладывать от любой точки), при этом будем получать векторы, равные данному. Таким образом, свободный вектор определяет целый класс равных ему векторов, отличающихся только точкой приложения. Далее будут рассматриваться, как правило, свободные векторы, при этом слово «свободные» будет опускаться.

2. Отношение равенства векторов является отношением эквивалентности. В самом деле, для отношения равенства ( — «вектор равен вектору «), определенного на множестве упорядоченных пар векторов, выполняются следующие условия:

а) каждый вектор равен самому себе (рефлексивность);

Это означает, что множество векторов разбивается на непересекающиеся классы (см. разд.В.З), т.е. с каждым вектором связывается целый класс равных ему векторов, отличающихся только точками приложения. Поэтому говорят [37], что свободный вектор определяет класс равных ему векторов.

Используя это построение, можно дать эквивалентные определения коллинеарности и компланарности. Два ненулевых вектора называются коллинеарными, если после приложения их к одной точке они лежат на одной прямой. Три ненулевых вектора называются компланарными, если после приложения их к одной точке они лежат в одной плоскости.

5. Кроме свободных векторов в приложениях векторной алгебры используются скользящие векторы, связанные (приложенные) векторы и др., которые отличаются от свободных векторов определением равенства. Например, скользящие векторы называются равными, если они лежат на одной прямой, одинаково направлены и имеют равные длины. Другими словами, в отличие от свободного вектора, скользящий вектор можно переносить, не меняя направления и длины, только вдоль содержащей этот вектор прямой. Например, в механике сила, действующая на абсолютно твердое тело, изображается скользящим вектором, а угловая скорость — свободным вектором. Сила, действующая на деформируемое тело, является примером так называемого приложенного вектора. Изменение точки приложения силы приведет к изменению ее воздействия на тело.

Пример 1.1. Дан треугольник (рис. 1.6), точки — середины его сторон. Для векторов, изображенных на рис. 1.6, указать коллинеарные, одинаково направленные, противоположно направленные, равные.

Источник