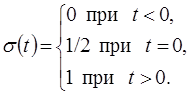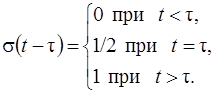что такое тестовый входной сигнал
Тестовые сигналы
Характеристики электрических цепей
Свойства электрической цепи определяются реакцией ее на то или иное воздействие. В качестве воздействий в теории цепей принимают элементарные тестовые сигналы. Реакции цепи на эти сигналы и определяют ее характеристики. Тестовые сигналы должны отвечать следующим требованиям.
1. Расчет или экспериментальное определение реакции цепи на их воздействие должны быть достаточно простыми.
2. Суммой тестовых сигналов должно определяться любое сложное воздействие на цепь.
Выполнение этих требований дает возможность при расчете реакции цепи на сложное воздействие применять принцип суперпозиции:
1) находим реакцию цепи на тестовый сигнал (т.е. характеристику цепи);
2) представляем реальный сигнал суммой тестовых сигналов;
3) складываем реакции цепи на каждый тестовый сигнал в отдельности и получаем реакцию цепи на реальный сигнал.
В качестве тестовых сигналов применяют:
— гармоническую функцию единичной амплитуды u = cosωt, u = sinωt или u = expjωt;
— единичный скачок (функцию Хевисайда) σ(t);
— единичный импульс (дельта-функцию Дирака) δ(t).
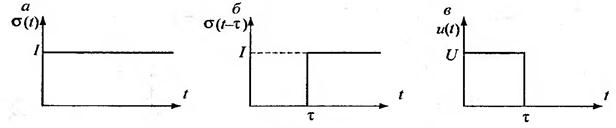
Единичный скачок имеет вид, показанный на рис. 2.1, а.
Функция σ(t) определяется следующим образом:
Функция σ(t), запаздывающая на время τ, приведена на рис. 2.1, б. Она определяется следующим образом:
Такими функциями можно представить любые импульсные функции. Например, прямоугольный импульс амплитудой U и длительностью τ (рис. 2.1, в) можно описать как u(t) = Uσ(t) – Uσ(t-τ).
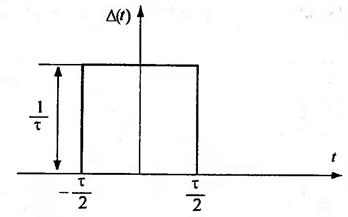
Единичный импульс, или дельта-функция Дирака, определяется как предел импульса δ(t) при τ→0 (рис. 2.2).
При τ→0 длительность импульса стремится к 0, а амплитуда к ∞. Но площадь импульса 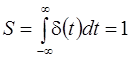
Суммой дельта-функций можно представить любое сложное воздействие.
Единичный скачок и единичный импульс связаны между собой соотношениями
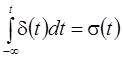
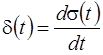
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Тестовые входные сигналы
Важнейший интерес при анализе качества представляет поведение систем управления во времени, т. к. эти системы объективно являются динамическими. Прежде всего необходимо определить, устойчива ли система управления (методы анализа устойчивости будут рассмотрены в последующих главах). Если она устойчива, то показатели качества можно оценить по реакции системы на определенный входной сигнал. Но, поскольку обычно заранее неизвестно, каким в реальных условиях будет этот сигнал, при анализе качества выбирается некоторый тестовый входной сигнал. Такой подход вполне оправдан, т. к. имеется корреляция между реакцией системы на типовой входной сигнал и ее поведением в реальных рабочих условиях. Кроме того, использование типового входного сигнала позволяет проектировщику сравнить несколько вариантов создаваемой системы. К тому же многие системы управления в процессе эксплуатации подвергаются внешним воздействиям, которые по виду очень близки к тестовым сигналам.
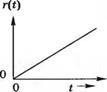
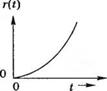
В качестве типовых тестовых сигналов обычно используются ступенчатый, линейный и параболический сигналы, изображенные на рис. 5.2. В табл. 5.1 приведены выражения для этих сигналов как функции времени, а также их преобразования по Лапласу, полученные с помощью табл. 2.3. Линейный сигнал является интегралом от ступенчатого, а параболический — интегралом от линейного.
Рис. 5.2. Тестовые входные сигналы:
(а) ступенчатый, (б) линейный, [в) параболический
Таблица 5.1. Тестовые входные сигналы
Г S(t)dt = l, Г b(t-a)g(t)dt=g(a). (5.1)
Импульсный входной сигнал может оказаться полезным, когда выходной сигнал jy(/) записывается в виде интеграла свертки
Эта связь изображена в виде структурной схемы на рис. 5.3. Если входной сигнал является единичной импульсной функцией, то
Датчики и микроконтроллеры. Часть 1. Матчасть
В этом цикле я расскажу о датчиках — как о немаловажном элементе системы управления неким объектом или тех. процессом.
Все свое повествование я буду вести касаемо практических вопросов реализации цифровых систем управления на базе микроконтроллеров.
Введение
В системе управления технологической установкой снятие текущих показаний некоторой величины — температуры, влажности, давления, уровня жидкости, напряжения, тока и проч. осуществляется с помощью датчиков — устройств и механизмов, предназначенных для преобразования сигнала внешнего воздействия в форму, понятную системе управления. Например, датчик влажности генерирует электрический сигнал, пропорциональный текущему значению влажности воздуха.
Как правило, датчики используются не сами по себе, а входят в состав системы управления, обеспечивая сигнал обратной связи. 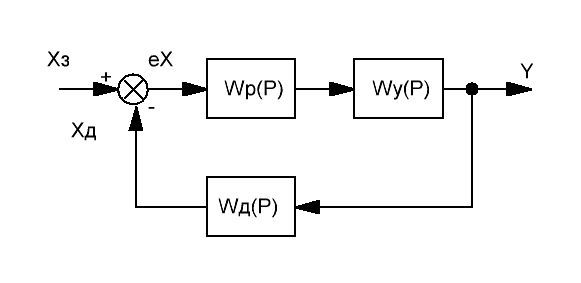
Рисунок 1. Типовая схема замкнутой системы регулирования
На рисунке 1 представлена типовая схема системы регулирования. Имеется сигнал задания Xз, который сравнивается с сигналом на выходе, получаемым с помощью датчика, имеющего передаточную функцию Wд(p). Ошибка управления подается на регулятор, который, в свою очередь, формирует сигнал управления исполнительным узлом, формирующим выходной сигнал Y.[1]
Простой пример — центробежный регулятор частоты вращения двигателя, где датчиком является платформа с шарами, которая, вращаясь, устанавливает то или иное положение топливной рейки. Заслонка, управляемая этой рейкой, регулирует количество топлива, подаваемое на двигатель. Сигналом задания будет являться требуемое значение скорости.
1.1 Классификация датчиков
Следует отметить, что в литературе встречается и альтернативный вариант классификации, когда Генераторные датчики определяются как Активные, а Параметрические — как Пассивные. Здесь и далее я руководствуюсь вариантом согласно справочнику Фарйдена.
2 Характеристики датчиков
Большинство датчиков имеют сложную процедуру преобразования измеряемой величины в электрический сигнал. Например, в тензорезисторном датчике давления измеряемая величина воздействует на чувствительный элемент, изменяя его сопротивление. После подачи сигнала возбуждения, падение напряжения на резисторе позволит косвенно определить его сопротивление и, на основании зависимости сопротивления от давления, вычислить измеряемую величину.
Для разработчика датчик представляет собой черный ящик с известными соотношениями сигналов между входами и выходами.
2.1 Диапазон измеряемых и выходных значений
Диапазон измеряемых значений показывает, какое максимальное значение входного сигнала датчик может преобразовать в выходной электрический сигнал, не выходя за пределы установленных погрешностей. Данные цифры всегда приводятся в спецификации на датчик, одновременно отображая возможную точность измерений в том или иной диапазоне.
Следует понимать, что одни датчики при подаче входного сигнала больше максимальных значений просто войдут в насыщение и будут возвращать неверные данные. Другие же датчики (например датчики температуры) могут выйти из строя. В дальнейшем, для каждого типа датчика будут даны свои рекомендации.
Диапазон выходных значений датчика — это минимальное и максимальное напряжение, которое датчик способен выдать при минимальном и максимальном внешнем воздействии. Так как мы рассматриваем датчики, преобразующие входной сигнал в электрический, то диапазон выходных значений датчика будет определяться в вырабатываемом им напряжении, или пропускаемом через него токе. Одной из наших задач при подключении датчика будет согласование выходного диапазона датчика со входным диапазоном измерительного тракта.
2.2 Передаточная функция — статические и динамические характеристики
При работе с датчиком требуется знать соотношение уровней сигналов на входе и выходе. Отношение Wд(p) = Y(p)/X(p) в операторном виде является передаточной функцией датчика и однозначно определяет характеристики датчика в статике и динамике.
Уравнение Y(p) = Wд(p)*X(p) в реальной плоскости, т.е. функция Y = f(x) будет являться статической характеристикой
Статическая характеристика может быть линейно и будет определяться как:
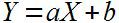
Где a – наклон прямой, определяемый чувствительностью датчика и b – постоянная составляющая(т.е. уровень выходного сигнала при отсутствии сигнала на входе)
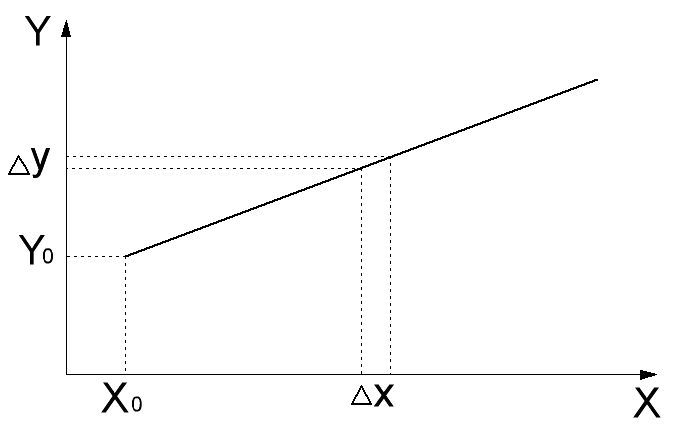
Рисунок 2. Линейная зависимость
Помимо датчиков с линейной зависимостью, могут быть датчики с логарифмической зависимостью, с уравнением вида
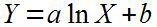
Экспоненциальной:

Или степенной:
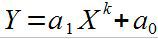
Где k – постоянное число.
Существуют датчики с более сложной характеристикой. Но на то есть документация.
Однако, передаточная функция раскрывает и то, какими свойствами обладает датчик в динамике, т. е. насколько быстро и точно отрабатывает датчик выходной сигнал при быстром изменении входной величины. Практически каждый реальный датчик имеет в себе накопитель энергии — конденсатор, массу и т. п. Рассмотрим поведение датчика, динамические характеристики которого описываются уравнением первого порядка:
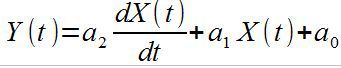
В теории автоматического управления существует два тестовых входных сигнала. Это единичная функция — подача в нулевой момент времени единицы, и дельта-функция — подача сигнала бесконечной амплитуды и бесконечно малой длительности.
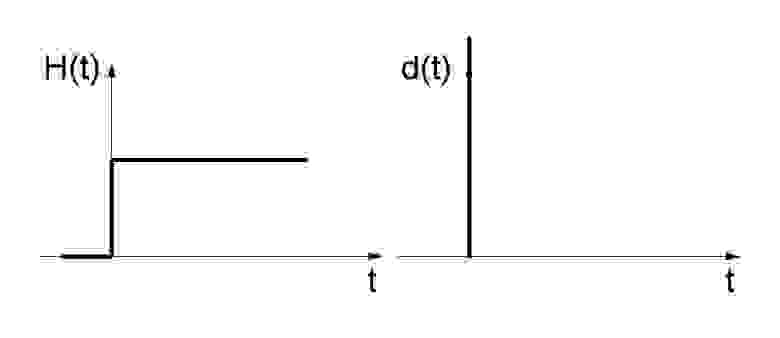
Рисунок 3. Единичная и дельта функции
Безынерционный, то бишь идеальный датчик в точности повторит форму входного сигнала. Реальный датчик, описанный формулой (5) выдаст следующую реакцию:
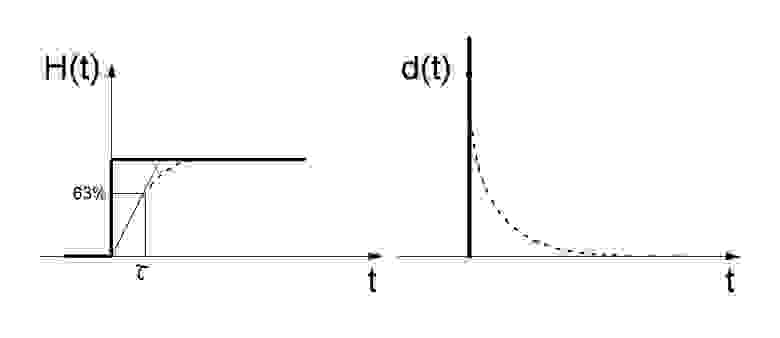
Рисунок 4. Реакция апериодического звена первого порядка на тестовые сигналы
Следует отметить, что значение на выходе датчика будет соответствовать поданному на входе только после завершения переходного процесса, которое будет длиться 3-4τ, где τ — постоянная времени нашего звена. При t=1τ, выходное значение достигнет 
Нетрудно посчитать, что при t = 2τ выходное значение составит 86%, а при t = 3τ — 95% и переходный процесс будет считаться завершенным.
Таким образом нужно понимать, что, например, тот же датчик температуры будет реагировать на изменение температуры окружающей среды с некоторым запаздыванием из-за того, что между датчиком и окружающей средой имеется корпус, который должен поглотить тепло и нагреться. На это требуется время.
Разумеется, инерционные датчики могут описываться более сложными уравнениями, например представляться апериодическими звеньями второго порядка, иметь задержку реакции и т. д. Особенности поведения таких звеньев подробно описаны в [1].
2.3 Точность, нелинейность
Одной из важных характеристик датчика является его точность в диапазоне измеряемых величин. Выходной сигнал датчика соответствует значению измеряемой величины с некоторой достоверностью, называемой погрешностью.
Например, датчик температуры имеет точность ±2 градуса. Это означает, что при реальной температуре измеряемого объекта в 100 градусов, допустимые показания данного датчика температуры находятся в пределах 98 – 102 градусов.
Погрешность датчика бывает разной.
Различают аддитивную и мультипликативную погрешность.
Аддитивная погрешность постоянна во всем диапазоне измерений. 
Рисунок 5. Аддитивная погрешность
Мультипликативная линейно зависит от уровня измеряемой величины: 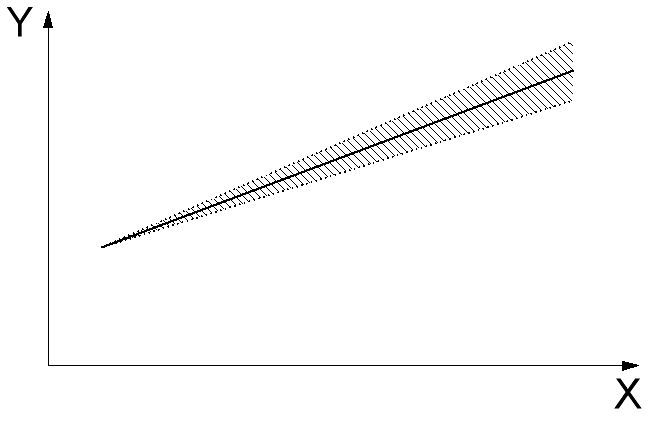
Рисунок 6. Мультипликативная погрешность
Кроме того, существует нелинейность датчика в измеряемом диапазоне. В зависимости от текущего диапазона измерения, коэффициент наклона передаточной функции изменяется в некоторых пределах. При этом, в спецификации указываются либо кривые изменения точности по диапазону, либо худшие показатели нелинейности в том или ином диапазоне.
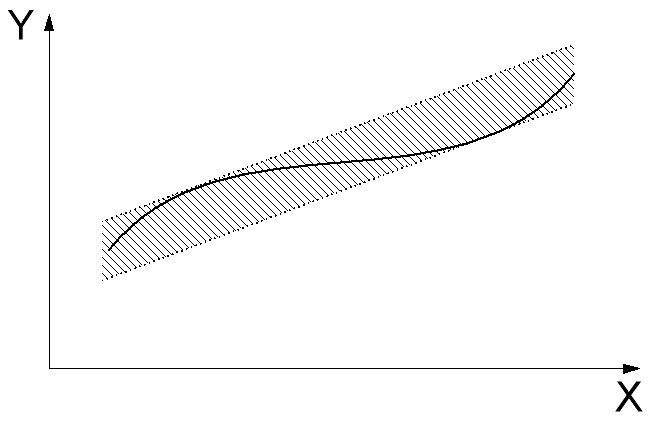
Рисунок 7. нелинейность датчика
Кроме того, некоторые датчики имеют эффект гистерезиса, когда для одного и того же входного сигнала после возрастания и убывания значения выходного сигнала получаются разными. Типичной причиной гистерезиса является трение и структурные изменения материалов. Наибольшему эффекту гистерезиса подвержены датчики на основе ферромагнитных материалов.
Для повышения точности и компенсации аддитивной и мультипликативной погрешности может производиться процесс калибровки датчика. Например, для линейного датчика необходимо с заведомо известной точностью определить показания в двух точках, находящиеся на разных концах рабочего диапазона. Для некоторых датчиков данные калибровки могут приводиться в паспорте на каждый конкретный экземпляр. Для проведения процедуры калибровки можно воспользоваться более точной аппаратурой, можно воспользоваться эталоном (например черное тело, эталонный килограмм и т. п.). Точность после калибровки естественно не сможет превышать точность эталона.
2.4 Чувствительность датчика, разрешающая способность и мертвая зона
Мертвая зона датчика — это нечувствительность датчика в определенном диапазоне входных сигналов. В пределах этой зоны выходные показания некорректны.
Для примера на рисунке 2 показания выходной величины для всех значений от 0 до x0 не определены. Такой особенностью грешат, например, некоторые датчики тока, имеющие нулевое напряжение на выходе при токах меньших, к примеру, 10мА.
Во всем остальном диапазоне имеет место определенная чувствительность датчика, т. е. насколько силен прирост выходного сигнала на изменение входного сигнала. т. е. чувствительность определяется следующей формулой: 
Для линейного датчика, чувствительность будет постоянной на всем измеряемом диапазоне.
Разрешающая способность показывает, насколько малое изменение измеряемой величины способно вызвать изменение выходного сигнала. Например, какой-нибудь инкрементальный датчик положения имеет разрешающую способность в 1 градус. Аналоговые датчики обладают бесконечно большим разрешением, так как в их выходном сигнале нельзя определить отдельных ступеней его изменения.
3 Способ подключения датчиков
В зависимости от типа датчика, подключается он к измерительному тракту по-разному.
Подключение пассивного датчика
Так как пассивный датчик без посторонней помощи в ответ на внешнее воздействие самостоятельно вырабатывает для нас электрический сигнал, нам этот сигнал нужно считать.
В зависимости от того, будет ли наш датчик источником тока или источником напряжения, способ подключения будет отличаться.
К примеру, термопара является источником напряжения — напряжение на выходе не зависит от величины выходного тока (в разумных пределах конечно). Наша задача — измерить вырабатываемую ЭДС. Так как измерительный тракт будет иметь некоторое конечное сопротивление, схема подключения будет следующей: 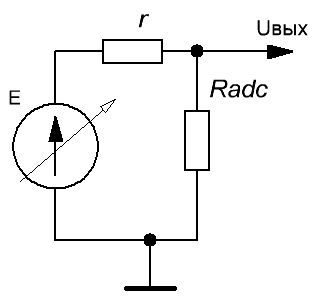
Рисунок 8. Подключение источника напряжения к АЦП
Если Radc будет много больше внутреннего сопротивления r, тогда падение напряжения на нем будет стремиться к нулю и напряжение на входе АЦП будет стремиться к значению ЭДС.
Во второй части я подробно рассмотрю термопару, как один из самых точных и быстродействующих датчиков.
Другой случай, если наш датчик является источником тока, т.е генерируемое им напряжение зависит от пропускаемого через нагрузку тока.
Подключение датчика аналогично: 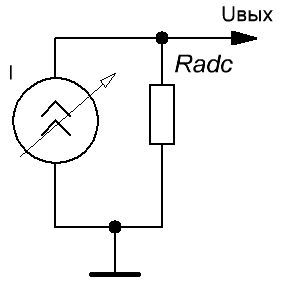
Рисунок 9. Подключение источника тока к АЦП
Однако, сопротивление нагрузки источника тока теперь должно стремиться к нулю. Для этого, датчик шунтируется резистором необходимого сопротивления, превращая тем самым, источник тока в источник напряжения: 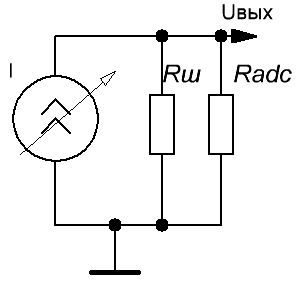
Рисунок 10. Правильное подключение источника тока к АЦП
Сопротивление резистора Rш рассчитывается как частное от деления максимального напряжения, подаваемого на вход АЦП на максимальный ток, который способен выдать датчик 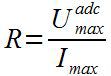
Наиболее яркий представить такого датчика — датчик тока.
ВНИМАНИЕ: датчики, имеющие схему замещения в виде источника тока, следует обязательно шунтировать сопротивлением и не допускать обрыва цепи шунтирования при наличии сколь угодно малого входного воздействия. В противном случае, тот же датчик тока генерирует на свободных клеммах вторичной обмотки напряжение в киловольты до пробоя схемы измерения или самого датчика. Современные датчики тока тестируют на напряжении 1кВ и более, так что получить на выходе 2-3кВ, а еще попасть в них пальцем — не самая сложная задача.
Подключение активного датчика
Рассмотрим активные датчики, представляющие собой переменное сопротивление. В частности это терморезисторы, тензорезисторы и прочие подобные датчики. Чтобы сопротивление датчика измерить, его необходимо подключить к источнику тока и определить падение напряжения на нем:

Рисунок 11. Подключение датчика к нерегулируемому источнику тока
Источник тока вырабатывает ток постоянного значения известной величины. Тогда, выходное напряжение будет определяться по формуле:

Например, рассчитаем выходное значение напряжения при токе источника 10мА если наш датчик изменяет сопротивление от 0,1кОм до 1 кОм. Тогда максимальное выходное напряжение будет равно 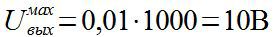
Что вполне соответствует требуемому значению напряжения для аналоговой системы управления на базе операционных усилителей.
Где взять источник тока? Бывает так что он встроен в сам микроконтроллер. Например в микроконтроллерах ADuCM360/361 есть два встроенных источника тока 0,01-1мА. Правда там у них диагностическая задача — подавая малый ток через цепи датчика можно убедить в его наличии и исправности.
Конечно, нам привычнее использовать источник напряжения с делителем: 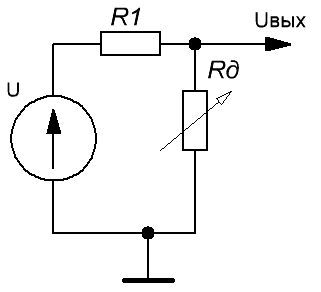
Рисунок 12. Подключение датчика к источнику напряжения с делителем
Если говорить на чистоту, то цепочка U-R1 образует тот же самый источник тока, только его параметры зависят от нагрузки — Rд. Напряжение на выходе будет определяться по следующей формуле:
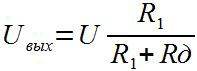
И тут всплывает главная проблема такого метода — от сопротивления нашего датчика в знаменателе не избавишься никак и показания становятся нелинейными, в отличие, кстати, от первого варианта.
С другой стороны, максимальное выходное напряжение у нас ограничено входными цепями измерительного устройства. Например, на вход микроконтроллера с питанием 5В необходимо подать напряжение, к примеру, не более 2,5В. Отмечу, что если максимально возможное напряжение, подаваемое на вход АЦП меньше напряжения питания, то мы сможем его туда подать.
Если наш датчик изменяет сопротивление от 0,1кОм до 1 кОм, то примем сопротивление резистора R1 равное верхней границе сопротивления датчика. Тогда Uвых сможет изменяться в пределах от 1/11Uвх до 1/2Uвх. В абсолютных цифрах данного примера — от 0,45 до 2,5В. И такими значениями мы используем (2,5-0,45)/2,5 = 82% всего диапазона АЦП, что довольно неплохо.
Еще датчик можно воткнуть в состав измерительного моста и измерять разницу напряжений в его плечах:
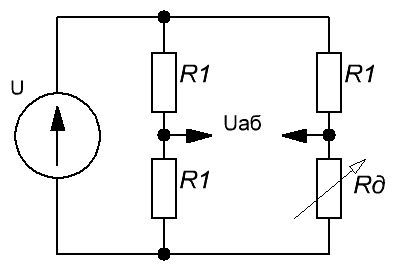
Рисунок 13. Датчик в составе измерительного моста
В этом случае мы работаем с дифференциальным АЦП, измеряя разность потенциалов Uab. Она будет равна: 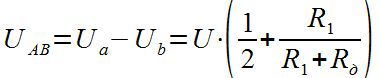
Причем сопротивление резистора R1 может быть таким, чтобы Uab могло быть и отрицательным. Существуют датчики, внутренняя схема которых уже представляет собой балансный мост с необходимыми характеристиками. Позднее я рассмотрю примеры таких датчиков.
Существуют более удобные в использовании датчики. Они выдают необходимый аналоговый сигнал и без танцев с резисторами. Например, аналоговый датчик влажности HIH-4010-004 — трехвыводной корпус, 5В питание, линейный выход. Подключается это чудо так:
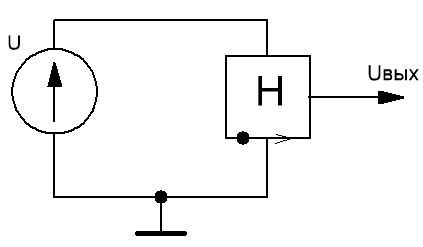
Рисунок 14. Подключение датчика влажности HIH-4010-004
Два провода к источнику опорного напряжения, выход — к АЦП микроконтроллера.
Подключение цифровых датчиков по стандарту 1-Wire
1-Wire это двунаправленная низкоскоростная цифровая шина передачи данных, требующая всего два провода — информационный провод и землю. Шина достаточно проста в использовании, поддерживает паразитное питание устройств от линии и позволяет подключать параллельно множество однотипных устройств вроде датчиков температуры(всеми любимыми DS18B20), или микросхем идентификации (iButton).
Паразитное питание организовывается следующим образом:
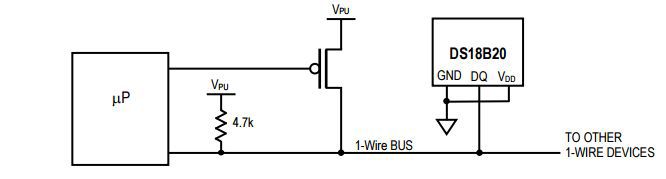
Рисунок 15. Паразитное питание устройств шины 1-Wire
А это обычное активное питание устройства, когда до источника рукой подать. 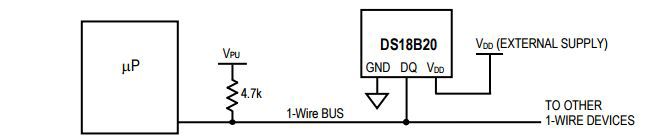
Рисунок 16. Питание устройства 1-Wire от внешнего источника
Количество подключенных параллельно датчиков фактически ограничено лишь параметрами линии.
Возможно горячее подключение и идентификация на ходу. Причем вычислительная сложность алгоритма идентификации O(log n)
Более подробно с этим протоколом мы поработаем во второй части.
А пока, про сам протокол можно почитать по классической ссылке: http://datasheets.maximintegrated.com/en/ds/DS18B20.pdf
Подключение цифровых датчиков по стандарту I2C(Twi)/SMBus
Если 1-Wire требовала один провод данных, то эта шина, исходя из названия Two-Wire Bus — два.
Один из проводов — SCL будет тактирующим, по второму — SDA, полудуплексом будут передаваться данные.
Шина с открытым коллектором, следовательно обе линии необходимо подтянуть к питанию. Датчик будет подключаться следующим образом:

Рисунок 17. Подключение датчиков по I2C
Общее количество устройств, которые можно подключить к шине I2C — 112 устройств при 7-разрядной адресации. Каждому устройству на деле выделяется два последовательных адреса, младшим битом выставляется режим — на чтение или запись. Есть строгое требование по емкости шины — не более 400пФ.
Общеупотребительные значения скоростей — 100 кбит/сек и 10 кбит/сек, хотя последние стандарты допускают и скоростные режимы в 400 кбит/сек и 3.4мбит/сек.
Шина может работать как с несменяемым мастером, там и с передачей флага.
Огромное количество информации по протоколу можно найти по этой ссылке: http://www.esacademy.com/en/library/technical-articles-and-documents/miscellaneous/i2c-bus.html
Подключение цифровых датчиков по стандарту SPI
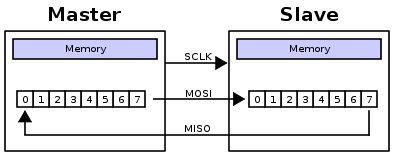
Рисунок 18. подключение по SPI и суть передачи
Каждое устройство в цепи содержит свой сдвиговый регистр данных. С помощью сигналов тактирования, спустя 8 тактов содержимое регистров меняется местами, тем самым, осуществляя обмен данными.
SPI — Самый скоростной из представленных интерфейс передачи данных. В зависимости от максимально-возможных частот тактирования скорость передачи данных может составлять 20, 40, 75 мбит/сек и выше.
Шина SPI позволяет подключать устройства параллельно, но здесь возникает проблема — каждому устройству требуется своя линия CS до процессора. Это ограничивает общее количество устройств на одном интерфейсе.
Главная сложность в настройке SPI — это установить полярность сигнала тактирования. Серьезно. Настроить SPI не просто, а очень просто.
Коротко и ясно об SPI с описанием периферийных модулей SPI для AVR и MSP430 можно прочитать здесь http://www.gaw.ru/html.cgi/txt/interface/spi/index.htm
4 Снятие показаний с датчиков
Пора бы уже прочесть с наших датчиков хоть какую-то информацию.
В зависимости от способа подключения датчика и его типа возможны различные способы снятия показаний. Следует отметить, что некоторые датчики, например цифровые датчики, или датчики состава газа, требуют предварительного запуска режима измерения, который может длиться некоторое время.
Таким образом, процесс измерения состоит из двух тактов — такт измерения данных и такт снятия данных. При организации программы можно пойти по одному из следующих вариантов: 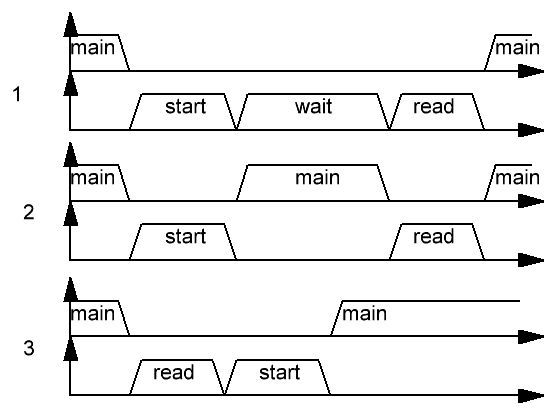
Рисунок 19. Процесс считывания показаний с датчика
Рассмотрим каждый вариант по отдельности и набросаем скелеты:
Вариант 1. запустили режим измерений, подождали, считали.
Вариант притягателен своей простотой, однако за ней кроется проблема — во время ожидания выполнения измерений микроконтроллер нагло простаивает, не выполняя задач. В большинстве систем автоматики такой режим — непозволительная роскошь.
В коде это будет выглядеть следующим образом:
Вариант 2. запустили режим измерений, вернулись к другим задачам, по прошествии времени сработало прерывание, считали данные.
Один из лучших вариантов. Но наиболее сложный:
Выглядит неплохо. позволяет варьировать время между циклами измерений и циклами считывания. например, датчик состава газов должен успеть остыть после предыдущих измерений, либо успеть нагреться во время измерений. Это разные периоды времени.
Вариант 3: Считали данные, запустили новый виток.
Если датчик позволяет после считывания данных запускать новый цикл измерений, то почему бы и нет — сделаем все наоборот.
Отличный способ сэкономить время. и знаете что — такой метод отлично работает и без прерываний. Цифровые датчики хранят вычисленное значение вплоть до отключения питания.А с учетом того, что считывать сигналы с датчика влажности ввиду его инерционности в 15 секунд часто и не требуется, можно и вовсе сделать так:
Может быть и такой вариант, что наш датчик самостоятельно запускает новый цикл измерений и потом с помощью внешнего прерывания он сообщает о завершении измерений. Например, АЦП можно настроить на автоматический режим считывания данных с частотой N Гц. С одной стороны, в обработчике прерывания будет достаточно реализовать только процесс считывания новых данных. С другой стороны, можно воспользоваться прерыванием АЦП с режимом Прямого Доступа к Памяти — ПДП(DMA). В этом случае по сигналу прерывания периферийный модуль АЦП на аппаратном уровне самостоятельно скопирует данные в определенную ячейку памяти в ОЗУ, тем самым обеспечивая максимальную скорость обработки данных и минимальное воздействие на рабочую программу (не надо уходить в прерывание, вызывать обработчик и проч.).
Но использование DMA сильно выходит за рамки данного цикла.
К сожалению, первый метод поголовно используется в библиотеках и примерах для Arduino, не позволяет этой платформе правильно использовать ресурсы микроконтроллера. Зато он проще в написании и отладке.
4.1 Работа с АЦП
Имея дело с аналоговыми датчиками имеем дело с АЦП. В данном случае рассматривается АЦП встроенный в микроконтроллер. Так как АЦП является по сути тем же датчиком — преобразует электрический сигнал в информационный — для него справедливо все что описано выше в разделе 2. Главными характеристиками АЦП для нас являются его эффективная разрядность, чувствительность, опорное напряжение и быстродействие. При этом, выходным значением АЦП преобразования будет некоторое число в выходном регистре, которое необходимо перевести в абсолютное значение в единицах измеряемой величины. В дальнейшем, для отдельных датчиков будут рассмотрены примеры таких расчетов.
4.1.1 Опорное напряжение
Опорное напряжение АЦП — это напряжение, которому будет соответствовать максимальное выходное значение АЦП. Опорное напряжение подается от источника напряжения, как встроенного в микроконтроллер, так и внешнего. От точности этого источника зависит точность показаний АЦП. Типовое опорное напряжение встроенного источника равняется напряжению питания или половине напряжения питания микроконтроллера. Могут быть и другие значения.
Например, таблица возможных значений опорного напряжения для микроконтроллера Atmega1280: 
Рисунок 20. Выбор опорного напряжения для АЦП микроконтроллера Atmega1280
4.1.2 Разрядность АЦП и чувствительность
Разрядность АЦП определяет максимальные и минимальные значения в выходном регистре при минимальном и максимальном входном воздействии электрического сигнала.
Следует отметить, что максимальная разрядность АЦП может не соответствовать его эффективной разрядности.
Часть младших разрядов может быть отдана на шум. Обратимся к датащиту на микроконтроллер ADuCM360, имеющему 24-разрядный АЦП с эффективной разрядностью 14 бит:

Рисунок 21. Назначение битов регистра данных АЦП
Как видно из рисунка, в 32-разрядном регистре, часть выделяется на знак, часть на нули и часть на шум. И лишь 14 разрядов содержат данные, имеющие указанную точность. В любом случае, эти данные всегда указываются в документации.
От эффективной разрядности АЦП зависит его чувствительность. Чем больше промежуточных ступеней выходного напряжения, тем выше будет чувствительность.
Допустим, опорное напряжение АЦП Uоп. Тогда, N-разрядный АЦП, имея 2N возможных значений, имеет чувствительность 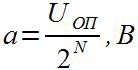
Таким образом, для 12-разрядного АЦП и опорного напряжения в 3,3В его чувствительность составит 3,3/4096 = 0,8мВ
Так как наш датчик также обладает определенной чувствительностью и точностью, будет неплохо, если АЦП будет обладать лучшими показателями
4.1.3 Быстродействие АЦП
Быстродействие АЦП определяет, насколько быстро считываются показания. Для АЦП последовательного приближения требуется определенное количество тактов, чтобы оцифровать уровень входного напряжения. Чем больше разрядность, тем требуется больше времени, соответственно, если к концу измерения уровень сигнала успевает измениться, это отразится на точности измерения.
Быстродействие АЦП измеряется в количестве семплов данных в секунду. Оно определяется как частота сигнала тактирования АЦП, деленная на требуемое для измерения число таков. Например, имея частоту тактирования АЦП в 1МГц и 13 тактов для снятия показаний, быстродействие АЦП будет равно 77 килосемплов в секунду. Для каждого варианта разрядности возможно рассчитать свое быстродействие. В технической документации обычно указывается максимально-возможная частота тактирования АЦП и его максимальное быстродействие при той или иной разрядности.
4.2 Цифровые датчики
Главное преимущество цифровых датчиков перед аналоговыми — они предоставляют информацию об измеряемой величие в готовом виде. Цифровой датчик влажности вернет абсолютное значение влажности в процентах, цифровой датчик температуры — значение температуры в градусах.
На этом я закончу общий материал. В следующей части мы рассмотрим датчики HVAC с примерами.
После датчиков пойдет рассмотрение исполнительных устройств — там довольно много интересного с точки значения теории автоматического управления, а потом доберемся и до синтеза и оптимизации регулятора всего этого безобразия.
UPD: Выражаю благодарность amartology, Arastas и Stross за справедливые замечания по статье. Добавил материал по 2 и 4 разделам и пояснил некоторые спорные моменты.