что такое теория вероятности в жизни
Теория вероятности в обычной жизни: можно ли применить ее без погрешностей?
Теория вероятностей (тервер) – раздел математики, который изучает случайные события и их свойства. Ознакомиться с ней нужно, чтобы понимать, как принимать взвешенные решения. Ведь зная статистические данные и анализируя закономерности, можно «предсказать» исход события.
Я не станут грузить вас сложными формулами – желающие углубленно заняться тервером могут сделать это по книге В. Е. Гмурмана «Теория вероятностей и математическая статистика». В статье покажу простые примеры для понимания зависимых и независимых событий, расскажу о состоянии неопределенности и интуитивном знании.
Материал полезен широкому кругу читателей.

Вероятность в зависимых событиях
Вы решаете отправить в подарок другу балык. Знаете номер дома, подъезд, этаж. Курьер просит называть номер квартиры. С мучительными усилиями вспоминаете, что в доме по три двери на площадку, но дальше – туман. Давайте рассчитаем, сможет ли курьер попасть в нужную квартиру с первого раза.
Имеем три варианта развития событий:
Но в истории участвует еще один человек: ваш друг. И событийность в его случае выглядит так:
Прежде чем пойти дальше, введем определение вероятности – количество благоприятных исходов к вероятному числу событий.
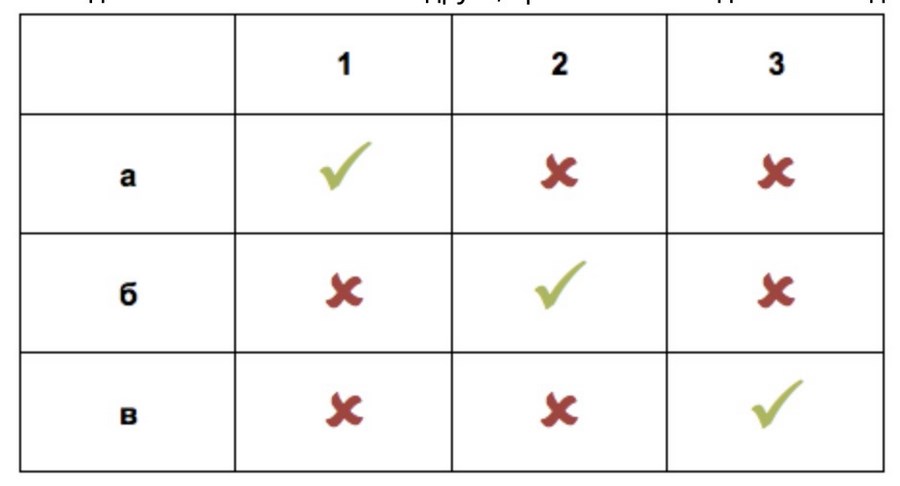
Представим, что курьер ошибся, и за дверью оказалась сногсшибательная блондинка в коротком халате. Для курьера исход положительный, для вас – нет. Поэтому считаем новую вероятность:
То же самое с другом:
Теперь у нас 4 варианта и 2 – выигрышные (таблица 2). Вероятность со второго раза попасть в квартиру друга – 1/2. Она уменьшилась из-за зависимости событий: мы уже исключили неблагоприятный исход и расчёт нужно производить заново. Если курьер настолько невезуч, что промахнется во второй раз, вероятность попасть по адресу в третий раз – 100%. Опытным путем мы проверили, что за двумя предыдущими дверьми балык никто не ждет.
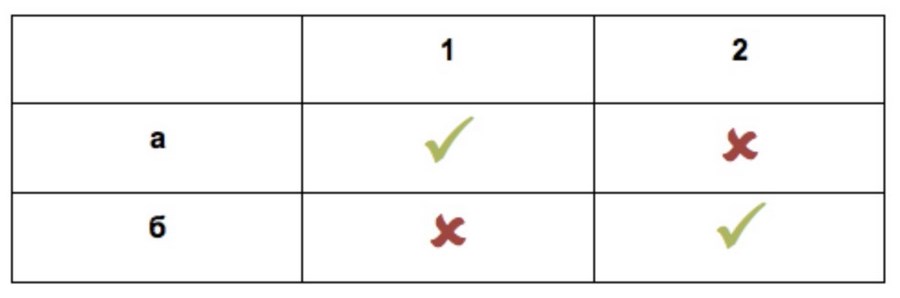
Пример с курьером — начальный уровень тервера. Он применим для бытовых нужд: предугадать вероятность побочного эффекта от антибиотиков, выбрать из разнообразия бабушкиных пирожков пирожок с повидлом и др.
На экзамене по теории вероятности советский математик и автор учебника Елена Вентцель спросила:
— Кому все понятно? Поднимите руки.
В аудитории живо взметнулся лес рук.
— Отлично! Остальные свободны, оценка – пять баллов! Поднявшие руки – останьтесь. За годы преподавания я так и не поняла большей части тервера. Рада, что вы мне все сейчас объясните.
Байка с математического факультета
У вас есть свой блог? Зарабатывайте с нами от 10 000 рублей на партнерской программе TeachLine.
Вероятность в независимых событиях
Независимые события не влияют друг на друга: количество благоприятных исходов в каждом новом событии не меняется.
Регина Тодоренко и Леся Никитюк в рамках программы «Орел и Решка» приехали в США. Обе хотят провести уик-энд «по богатому» и кидают монетку. Леся поставила на орла, Регина – на решку. Вероятность уехать на собственном авто у девушек одинакова: 1/2. На это раз повезло Лесе. Впрочем, как в следующей поездке тоже.

Теперь определим, могут ли независимые события происходить подряд с одним и тем же исходом. Лесе везло уже два раза и выпадал «орел». Повезет ли в третий раз? Составим список возможных исходов:
По результату видно: вероятность определенной последовательности каждый раз меньше на вероятность одного события. То есть вероятность определенной последовательности – произведение вероятностей каждого события. Если в одном событии вероятность 1/2, то в трех: 1/2*1/2*1/2=1/8.
Как человек принимает решения в состоянии неопределённости
Часть мозга, которая ответственна за оценку ситуации связана с медиаторной системой — центром мотивационных и эмоциональных процессов. Логика и эмоции часто конфликтуют между собой, поэтому решение принимается случайным образом.
У моей подруги аллергия на виноград. Но в студенчестве она не могла отказаться от бокала вина на вечеринке. Часто ее дерзость оставалась безнаказанной и организм нормально воспринимал аллерген. Реже протестовал: у подруги появлялись отеки на лице и в горле. В эти моменты ее левое полушарие отчаянно искало закономерность и просчитывало вероятность наступления аллергической реакции, правое же шептало: «Не пей, лицо распухнет!». Она могла вывести количество благоприятных исходов математическим путем и пить вино без опасений, но эмоции оказались сильней. Подруга раз и навсегда отказалась от любых продуктов с виноградом.
Хороший пример принятия решений описан в книге Млодинова «(Не) совершенная случайность». Допустим, вы отправили рассказ в четыре издательства. От каждого получили отказ. На эмоциях вы придете к мысли: рассказ ужасный! Хотя, если изучить биографии популярных писателей, может оказаться, что дело не в вас. Отказы в публикации получали Стивен Кинг, Джоан Роулинг, Виктор Франкл. Такие истории случались вовсе не из-за отсутствия у них дара: просто в одном издательстве редактор не понял тонкую философию автора, в другом – спешил домой и проставил визу не читая.
Почему интуитивное знание всегда противоречит статистике
Моя бабушка считает: в Албании убивают на каждом шагу. Хотя в стране она не была и новостей о не слышала: ей так кажется интуитивно. Наверняка и вы не раз испытывали подобное чувство. Оно называется интуитивное знание – внутреннее убеждение, что собственная оценка более правдива, чем официальные источники и статистика.

Классическое исследование на тему интуитивного знания провели Даниэль Канеман и Амос Тверский. Они дали задание группе студентов: на основании портрета, оценить утверждения с таблицы как более (1 балл) и менее (8 баллов) вероятные (таблица 3).
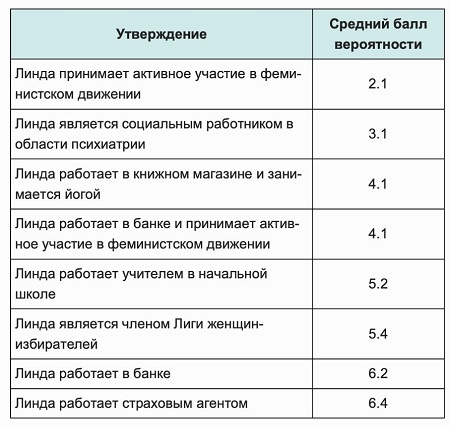
По портрету логично предположить, что Линда участвует в феминистском движении. Но студенты принимали решения интуитивно, что привело к ошибке. Вероятность, что Линда работает в банке и принимает участие в феминистском движении больше вероятности работы в банке.
Посмотрите на таблицу: вероятность работы в банке и увлечение феминистским движением – 4,1 балл. Но первое (работа в банке) и второе (феминистское движение) в сумме дают 8,3 балла. Согласно терверу, вероятность, что произойдут оба события не может быть выше, чем вероятность каждого события по отдельности. Главное утверждение (4,1 балла) содержит 2 события и является единым. В интуитивном решения правило тервера нарушено. Это доказывает — наши убеждения часто являются ложными.
В дальнейшем проводились множественные эксперименты, которые подтвердили догадку Канемана.
Вместо заключения
Теория вероятностей почти всегда разбивается о «случай», продиктованный убеждением или эмоцией отдельного человека. Поэтому использование ее в повседневной жизни может не оправдать ожиданий. Но выбирать вам! Хорошего дня!
Зачем нужна теория вероятностей в жизни
Именно под таким названием мы и провели вебинар — «Зачем нужна теория вероятностей в жизни».
В вебинаре мы не касались «жёлтых» тем типа «как выигрывать у казино» и «100% способ получить миллион без регистрации и SMS«.
Наоборот, были затронуты более серьёзные. Вот сам вебинар:
Идея похожего математического аппарата используется в Индии: можно купить билетик у мафии и кататься в общественном транспорте бесплатно, а полученные вами штрафы оплатит мафия. Называется «хафта» и выгодно вам и мафии, но не государству.
Подробно разбирается механизм лотереи — как идёт распределение средств и как происходит игра на эмоциях, когда одного победителя показывают по телевизору, а миллионы проигравших — нет. Эта идея была почерпнута из выступления на TED об ошибочных ожиданиях.
Также описывается открытие закона больших чисел и его применение сейчас.
А глядя на карту преступности страны, можно легко увидеть, что в одних регионах в 3 раза меньше шансов стать жертвой преступления, чем в других. Сам термин «уровень преступности» — статистический, это количественная характеристика преступности, и стоит отметить, что когда такой подход к оценке преступности был впервые представлен в 1832 во Франции, он вызвал смятение из-за стабильности полученных данных.
Ещё темы, затронутые в вебинаре:
Кстати, в анонсе вебинара использовался такой факт: в мае 2015 года Россия потеряла управление над космическим аппаратом «Прогресс». Как рассчитать, упадёт ли аппарат на сушу (или на конкретную страну). Сможете дать ответ? На наш взгляд, это отличный пример для иллюстрации геометрического подхода для расчёта вероятностей.
Теория вероятности в жизни людей
Основы теории вероятностей нужно знать каждому человеку для формирования правильного мировоззрения, для осознания того, что мы живем в случайном, вероятностном мире.
Психология человека такова, что ему неуютно среди случайностей. Он жаждет определенности и справедливости, ищет причин и объяснений. Часто таким образом возникают суеверия: например, среди африканских племен распространено поверье о том, что бывают просто львы и львы, в которых переселились души умерших. Последние на людей не нападают. Это объяснение не несет полезной информации, поскольку нет признаков, по которым заранее можно было бы определить, из какой категории лев, но оно успокаивает психологически. Точно так же появляются известные всем суеверия при сдаче экзаменов. Некоторые суеверия, кстати, основаны на частотных совпадениях (например, мелких неприятностей и встреч с черной кошкой). Это относится и к приметам, которые порой подмечают вероятностные закономерности. Так, поговоркам «Беда никогда не приходит одна» или «Жизнь, она полосатая» соответствует в теории вероятностей закон серий.
Следует помнить и то, что мы живем в мире, где происходят случайные события, и то, что закономерности пробиваются через массу случайностей. Чем сложнее система, тем труднее обнаружить закономерности. Именно в этих случаях и используют вероятностные методы. [4]
Таким образом, теория вероятности актуальна в наши дни как в математике и точных науках, так и в нашей повседневной жизни.
Теория вероятностей изучает объективные закономерности массовых случайных событий. Она является теоретической базой для математической статистики, занимающейся разработкой методов сбора, описания и обработки результатов наблюдений. Путем наблюдений (испытаний, экспериментов), т.е. опыта в широком смысле слова, происходит познание явлений действительного мира [1].
Теория вероятностей – раздел математики, изучающий закономерности случайных явлений, наблюдаемых при многократном повторении опыта [2, с.13].
Теория вероятностей – это раздел математики, изучающий закономерности случайных явлений: случайные события, случайные величины, их свойства и операции над ними [3].
Основные объекты теории вероятностей – случайные события, случайные величины, случайные процессы, то есть фактически весь окружающий нас мир [4, с.6].
Событие – это то, что может произойти или нет при выполнении определённого комплекса условий, или, как говорят, при проведении испытания. Среди возможных событий выделяют достоверные и невозможные. Если при каждом испытании всегда происходит некоторое событие, то оно называется достоверным. Если при испытании некоторое событие заведомо не может произойти, то оно называется невозможным. Если событие не является достоверным или невозможным, то оно часто называется случайным [5, с.10].
Во многих областях человеческой деятельности существуют ситуации, когда определённые явления могут повторяться неограниченное число раз в одинаковых условиях. Анализируя последовательно результаты таких простейших явлений, как подбрасывание монеты, игральной кости, выброс карты из колоды и т.п., мы замечаем две особенности, присущие такого рода экспериментам. Во-первых, не представляется возможным предсказать исход последующего эксперимента по результатам предыдущих, как бы ни было велико число проведённых испытаний. Во-вторых, относительная частота определённых исходов по мере роста числа испытаний стабилизируется, приближаясь к определённому пределу [6, с.8].
Рассмотрим теорию вероятностей на очень простых примерах. Если у нас в ящике лежит 10 пронумерованных шаров с цифрами от 1 до 10, то вероятность вытянуть шар с числом 10 равна 10 процентам. Но более вероятней, что мы вытянем любое другое число от 1 до 9, а не самое большое (не 10), поскольку такая вероятность составляет 90 процентов. Вытянуть шар с самым большим числом из 10000 пронумерованных шаров уже слишком маловероятно. Скорее всего, мы вытянем любое другое число (не 10000). При 10 миллионах шарах вытянуть самое большое число (10000000) практически невозможно [7].
Главным понятием теории вероятностей является вероятность. Это слово «вероятность», синонимом которого является, например, слово «шанс» достаточно часто применяется в повседневной жизни. Думаю, каждому знакомы фразы: «Завтра, вероятно, выпадет снег», или «вероятнее всего в выходные я поеду на природу», или «это просто невероятно», или «есть шанс получить зачет автоматом». Такого рода фразы на интуитивном уровне оценивают вероятность того, что произойдет некоторое случайное событие. В свою очередь математическая вероятность дает некоторую числовую оценку вероятности того, что произойдет некоторое случайное событие.
Теория вероятностей оформилась в самостоятельную науку относительно не давно, хотя история теории вероятностей началась еще в античности. Так, Лукреций, Демокрит, Кар и еще некоторые ученые древней Греции в своих рассуждениях говорили о равновероятностных исходах такого события, как возможность того, что вся материя состоит из молекул. Таким образом, понятие вероятности использовалось на интуитивном уровне, но оно не было выделено в новую категорию. Тем не менее, античные ученые заложили прекрасный фундамент для возникновения этого научного понятия. В средние века, можно сказать, и зародилась теория вероятности, когда были приняты первые попытки математического анализа, таких азартных игр как кости, орлянка, рулетка [8].
Первые подходы к оценке вероятности того или иного события были популярны еще в Средневековье среди «гамлеров» того времени. Однако тогда они имели лишь эмпирическое исследование (то есть оценка на практике, методом эксперимента) [9].
Первые научные работы по теории вероятностей появились в 17 веке. Когда такие ученые как Блез Паскаль и Пьер Ферма открыли некоторые закономерности, которые возникают при бросании костей. В ту же пору к данному вопросу проявлял интерес еще один ученый Христиан Гюйгенс. Он в 1657 в своей работе ввел следующие понятия теории вероятностей: понятие вероятности как величины шанса или возможности; математическое ожидание для дискретных случаев, в виде цены шанса, а также теоремы сложения и умножения вероятностей, которые правда не были сформулированы в явном виде. Тогда же теория вероятностей стала находить сферы своего применения – демографию, страховое дело, оценку ошибок наблюдений [8].
Вероятностные представления довольно успешно применялись ещё в 18 веке такими выдающимися учеными как Лаплас, Лагранж, Лежандр, Гаусс для оценки ошибок измерений, в результате чего уже в то время были заложены основы теории ошибок [10, с.3].
Дальнейшее развитие теории вероятностей привело к необходимости аксиоматизации теории вероятностей и главного понятия – вероятности. Так становление аксиоматики теории вероятностей произошло в 30 гг 20 века. Самый существенный вклад в заложение основ теории внес Космогоров А.Н.
На сегодняшний день теории вероятностей это самостоятельная наука, имеющая огромную сферу применения [8].
Последние десятилетия характеризуются резким повышением интереса к тем разделам математики и ее приложений, которые анализируют явления, носящие «случайный» характер. Эта тенденция в значительной степени объясняется тем, что большинство возникших в последние десятилетия новых математических дисциплин, которое ныне обозначается собирательным термином «кибернетика», оказалось тесно связанным с теорией вероятностей. Тем самым теория вероятностей стала чуть ли не самой первой по прикладному значению из всех математических дисциплин. При этом возникновение новых, в большинстве своем «порожденных» теорией вероятностей наук, скажем «теория игр», «теория информации», «страховая математика» или «стохастическая финансовая математика» привело к положению, при котором теорию вероятностей также приходится рассматривать как объединение большого числа разнородных и достаточно глубоко развитых математических дисциплин [10, с.4].
Людей всегда интересовало будущее. Человечество во все времена искало способ его предугадать, или спланировать. В разное время разными способами. В жизни мы часто сталкиваемся со случайными явлениями. Чем обусловлена их случайность – нашим незнанием истинных причин происходящего или случайность лежит в основе многих явлений? Споры на эту тему не утихают в самых разных областях науки. Случайным ли образом возникают мутации, насколько зависит историческое развитие от отдельной личности, можно ли считать Вселенную случайным отклонением от законов сохранения? [8]
Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки в том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса (в котором точно не обойтись без теории вероятности) на денежных опционах дает возможность зарабатывать на данной теории серьезные деньги.
Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны – все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. [9]
Решения чаще всего принимаются эмоционально. Люди боятся летать самолетами. А между тем, самое опасное в полете на самолете – это дорога в аэропорт на автомобиле. Но попробуй кому-то объяснить, что машина опасней самолета. Вероятность того, что пассажир, севший в самолет, погибнет в авиакатастрофе составляет примерно 1/8000000. Если пассажир будет садиться каждый день на случайный рейс, ему понадобится 21000 лет чтобы погибнуть. По исследованиям: в США в первые 3 месяца после терактов 11 сентября 2001 года погибло еще одна тысяча людей. косвенно. Они в страхе перестали летать самолетами и начали передвигаться по стране на автомобилях. А так как это опасней, то количество смертей возросло. По телевидению пугают: птичьим и свиными гриппами, терроризмом, но вероятность этих событий ничтожна по сравнению с настоящими угрозами. Опасней переходить дорогу по зебре, чем лететь на самолете.
Или другой пример – от падения кокосов погибает около 150 человек в год. Это в десятки раз больше, чем от укуса акул. Но фильма «Кокос-убийца» пока не снято. Подсчитано, что шанс человека быть подвергнутым нападению акулы составляет 1 к 11,5 млн, а шанс погибнуть от такого нападения 1 к 264,1 млн. Среднегодовое количество утонувших в США составляет 3306 человек, а погибших от акул 1. Миром правит вероятность и нужно помнить об этом. Они помогут вам взглянуть на мир с точки зрения случая [8].
Таким образом, теорию вероятностей нельзя не применять в нашей жизни. Она имеет разные области применения такие как: биологические и химические процессы, история, экономика, кораблестроение и машиностроение, медицина и большинство различной деятельности человека. Люди применяют её как сознательно, так и подсознательно, что проявляется в обычных повседневных фразах и действиях. Разумный человек должен стремиться мыслить, исходя из законов вероятностей. Теория вероятностей – это одна из составляющих частей успеха. Если стремиться учитывать законы вероятностей и, в том случае, если вероятность неблагоприятная, предпринимать соответствующие контрдействия, то можно упростить себе жизнь в разы и сэкономить своё время, которое так ценно для каждого из нас.
Список использованных источников
Савельева Р. Ю. Основы теории вероятностей и математической статистики [Электронный ресурс]. – Режим доступа: http://открытыйурок.рф/статьи/526665/ (дата обращения – 24.01.2018)
Кибзун А. И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами [Текст]: учебное пособие/А. И. Кибзун, Е. Р. Горяинова, А. В. Наумов, А. Н. Сиротин. – Москва: ФИЗМАТЛИТ, 2002. – 224 с.
Теория вероятностей и основные понятия теории [Электронный ресурс]. – Режим доступа: https://bookmaker-ratings.ru/wiki/teoriya-veroyatnostej-i-osnovny-e-ponyatiya-teorii/ (дата обращения 24.01.2018)
Крупкина Т. В. Теория вероятностей и математическая статистика [Текст]: учебное пособие/Т. В. Крупкина, С. В. Бабенышев, Е. С. Кирик. – Красноярск: Сибирский федеральный университет, 2007. – 199 с.
Семенов В. А. Теория вероятностей и математическая статистика [Текст]: учебное пособие/В. А. Семенов. – Санкт-Петербург: Питер, 2013. – 192 с.
Володин И. Н. Лекции по теории вероятностей и математической статистике [Текст]: учебник/И. Н. Володин. – Казань: (Издательство), 2006. – 271 с.
Вишня Ю. Теория вероятности в жизни [Электронный ресурс]. – Режим доступа: https://allowwonder.com/teoriya-veroyatnosti-v-zhizni/ (дата обращения – 6.02.2018)
Агеев В. В. Введение в теорию вероятностей [Текст]: учебно-методическое пособие/В. В. Агеев, М. С. Тихов. – Нижний-Новгород: ФГБОУВПО Нижегородский Государственный университет им. Н.И. Лобачевского Национальный исследовательский университет, 2012. – 32 с.
Что такое теория вероятности в жизни
Основы теории вероятностей изучаются в программе по математике каждой школы. Кроме того, задачи по данной дисциплине являются обязательной частью ОГЭ 9 и 11 классов.
Одной из важнейших сфер приложения теории вероятностей является экономика. В настоящее время невозможно себе представить исследование и прогнозирование экономических явлений без использования экономического моделирования, регрессионного анализа, трендовых и сглаживающих моделей и других методов, опирающихся на закономерности, которые изучаются в курсах теории вероятностей и математической статистики [1].
Также теория вероятностей имеет широкое применение таком направлении, как прогнозирование погоды в конкретный период. Поэтому возникает желание практически проверить, поможет ли данная наука для целей, решение которых необходимо в повседневной жизни.
Цель данной работы заключается в изучении особенностей применения теории вероятностей в жизни и анализе данных, полученных в ходе проведения практического эксперимента;
— изучить и проанализировать необходимую литературу по теме исследования;
— порешать ряд задач на классическое определение вероятности.
— экспериментально проверить применение вероятности в повседневной жизни.
Данная работа состоит из двух частей: «Глава 1. Теоретическая часть», «Глава 2. Экспериментальная часть», каждая из которых разбита на отдельные параграфы.
Объект исследования: применение теории вероятностей в жизни;
Предмет исследования: основы теории вероятностей;
Вероятностные идеи стимулируют в наши дни развитие всего комплекса знаний, начиная от наук о не живой природе и кончая науками об обществе. Прогресс современного естествознания неотделим от использования и развития вероятностных идей и методов. В наше время трудно назвать какую-либо область исследований, где бы не применялись вероятностные методы.
Гипотеза исследования: углубленное изучение данной темы позволит нам быть компетентными в вопросах экзаменов 9 и 11 классов;
Практическая значимость: Рассмотренный в ходе исследования материал обогащает жизненный опыт методами решения стандартных и нестандартных задач по теории вероятностей.
Глава 1 Теоретическая часть 1.1 История появления теории вероятностей
Французский дворянин, некий господин де Мере, был азартным игроком в кости и страстно хотел разбогатеть. Он затратил много времени, чтобы открыть тайну игры в кости. Он выдумывал различные варианты игры, предполагая, что таким образом приобретет крупное состояние. Так, например, он предлагал бросать одну кость по очереди 4 раза и убеждал партнера, что по крайней мере один раз выпадет при этом шестерка. Если за 4 броска шестерка не выходила, то выигрывал противник.
В те времена еще не существовала отрасль математики, которую сегодня мы называем теорией вероятностей, а поэтому, чтобы убедиться, верны ли его предположения, господин Мере обратился к своему знакомому, известному математику и философу Б. Паскалю с просьбой, чтобы он изучил два знаменитых вопроса, первый из которых он попытался решить сам. Вопросы были такие:
Сколько раз надо бросать две игральные кости, чтобы случаев выпадения сразу двух шестерок было больше половины от общего числа бросаний?
Как справедливо разделить поставленные на кон двумя игроками деньги, если они по каким-то причинам прекратили игру преждевременно?
Паскаль не только сам заинтересовался этим, но и написал письмо известному математику П. Ферма, чем спровоцировал его заняться общими законами игры в кости и вероятностью выигрыша.
Таким образом, азарт и жажда разбогатеть дали толчок возникновению новой чрезвычайно существенной математической дисциплины: теории вероятностей. В разработке ее основ принимали участие математики такого масштаба, как Паскаль и Ферма, Гюйгенс (1629—1695), который написал тракта «О расчетах при азартных играх», Яков Бернулли (1654—1705), Муавр (1667—1754), Лаплас (1749— 1827), Гаусс (1777—1855) и Пуассон (1781—1840). В наше время теория вероятности используется почти во всех отраслях знаний: в статистике, синоптике (прогноз погоды), биологии, экономике, технологии, строительстве и т. д [2].
1.2 Понятие теории вероятностей
Теория вероятностей – это наука о закономерностях случайных событий. Под случайным событием в теории вероятностей понимается всякое явление, которое может произойти или не произойти (случайным образом) при осуществлении определенного комплекса условий. Каждое такое осуществление называется испытанием, опытом или экспериментом.
События можно подразделить на достоверные, невозможные и случайные.
Достоверным называется событие, которое обязательно произойдет при испытании. Невозможным называется событие, которое заведомо не произойдет при испытании. Случайным называется событие, которое в результате эксперимента может либо произойти, либо не произойти (в зависимости от случайных обстоятельств).
Предметом теории вероятностей являются закономерности массовых случайных событий, где под массовостью мы понимаем многократную повторяемость.
Рассмотрим несколько событий:
появление герба при бросании монеты;
появление трех гербов при трехкратном бросании монеты;
попадание в цель при выстреле;
выигрыш по билету денежно-вещевой лотереи.
Очевидно, что каждое из этих событий обладает какой-то степенью возможности. Для того, чтобы количественно сравнивать между собой события по степени возможности, нужно с каждым событием связать определенное число.
Вероятность события есть численная мера степени объективной возможности этого события. В качестве единицы измерения вероятности принята вероятность достоверного события. Вероятность невозможного события равна нулю. Вероятность любого случайного события обозначается P и изменяется в диапазоне от нуля до единицы: 0 ≤ P ≤ 1.
Вероятностью случайного события называется отношение числа n несовместимых равновероятных элементарных событий, составляющих событие, к числу всех возможных элементарных событий N:
Возникновение теории вероятностей как науки относят к средним векам и первым попыткам математического анализа азартных игр (орлянка, кости). Первоначально её основные понятия не имели строго математического вида, к ним можно было относиться как к некоторым эмпирическим фактам, как к свойствам реальных событий, и они формулировались в наглядных представлениях [5].
1.3 Применение теории вероятностей в жизни
Например, не зная статистики, большинство людей склонны думать, что шанс погибнуть в авиакатастрофе больше, чем в автомобильной аварии. Теперь же мы знаем, изучив факты (о которых, думаю, многие наслышаны), что это совсем не так. Дело в том, что наш жизненный «глазомер» иногда дает сбой, потому что авиатранспорт кажется значительно страшнее людям, привыкшим твердо ходить по земле. Да и большинство людей не так часто используют этот вид транспорта. Даже если мы и может оценить вероятность события верно, то, скорее всего, крайне неточно, что не будет иметь никакого смысла, скажем, в космической инженерии, где миллионные доли решают многое. А когда нам нужна точность, то мы обращаемся к кому? Конечно же, к математике.
Примеров реального использования теории вероятности в жизни множество. Практически вся современная экономика базируется на ней. Выпуская на рынок определенный товар, грамотный предприниматель наверняка учтет риски, а также вероятности покупки в том или рынке, стране и т.д. Практически не представляют свою жизнь без теории вероятности брокеры на мировых рынках. Предсказывание денежного курса (в котором точно не обойтись без теории вероятности) на денежных опционах или знаменитейшем рынке Forex дает возможность зарабатывать на данной теории серьезные деньги.
Теория вероятности имеет значение в начале практически любой деятельности, а также ее регулирования. Благодаря оценке шансов той или иной неполадки (например, космического корабля), мы знаем, какие усилия нам нужно приложить, что именно проверить, что вообще ожидать в тысячи километров от Земли. Возможности теракта в метрополитене, экономического кризиса или ядерной войны — все это можно выразить в процентах. А главное, предпринимать соответствующие контрдействия исходя из полученных данных. Любую деятельность любой сферы можно проанализировать, использую статистику, рассчитать благодаря теории вероятности и заметно улучшить.
Глава 2 Практическая часть 2.1 Монета в теории вероятностей.
Монета сточки зрения теории вероятностей имеет только две стороны, одна из которых называется «орел», а другая – «решка». Монету бросают, и она падает одной из сторон вверх. Никакие другие свойства математической монете не присущи.
Проведём опыт. Для начала, возьмем в руки монетку, будем ее бросать и записывать результат последовательно. В нашем случае бросание монетки – это испытание, а выпадение орла или решки – событие, то есть возможный исход нашего испытания (см. Приложение 2).


